当前位置：首页 > news >正文

数据结构期中复习个人笔记

news 2025/11/3 9:17:50

一、绪论

1. 数据结构是一门研究非数值计算的程序设计问题中计算机的操作对象以及它们之间关系和操作等的学科。

个人理解：数据结构就是学习如何将数据在计算机中存储，以便达到空间利用最优和存取调用时间最优

2. 程序设计 = 数据结构 + 算法

3. 数据：客观事物的符号表示

数据元素：数据的基本单位

数据项：数据的最小单位

数据对象：性质相同的数据元素的集合，是数据的一个子集

4. 算法的五个特性：有穷性、确定性、可行性、输入、输出

5. 时间复杂度和空间复杂度

如果执行次数是确定的，不管执行次数多大，都是O(1)

二、线性表

1. 个人认为，线性表的可以认为是个表格，类似数据库中的关系。借助数据库来理解的话，每个元组就是一个数据元素，每一列代表数据项，在这数据元素可称为记录，而线性表称为文件

2. 线性表的顺序表示，是指用一组地址连续的存储单元依次存储线性表的数据元素。如果存储线性表的起始位置确定，线性表中的任一数据元素都可随机存取。顺序表是一种随机存取的存储结构。

线性表中存储和删除一个元素的时间复杂度是O(n)

#include<stdio.h>
#define INIT_SIZE 100
#define INCREMENT 10
typedef int ElemType; typedef struct
{ElemType* elem;    //基址int length;    //当前长度int listsize;   //可存储空间
}sqList;ElemType initList(sqList* L)
{L->elem=(ElemType*)malloc(INIT_SIZE*sizeof(ElemType));if(!L->elem) exit(1);   //安全性检查L->length=0;L->listsize=0;
}//在位置i插入元素e
//没有删除一说，实质上是数据的不断覆盖，无用的抛弃
int insertList(sqList* L,int i,ElemType e)
{if(i<1||i>L->length+1){printf("insert position error");return 0;}if(L->length>=L->listsize){ElemType* newbase=(ElemType*)realloc(L->elem,(L->length+INCREMENT)*sizeof(ElemType));if(!newbase) exit(1);L->elem=newbase;L->listsize +=INCREMENT;}ElemType* q=&(L->elem[i+1]);for(ElemType* p=(L->elem[L->length-1]);p>=q;p--) *(p+1)=*p;*q=e;L->length++;return 1;
}//删除位置i的元素，返回该位置元素内容
ElemType deleteList(sqList* L,int i,ElemType e)
{if(i<1||i>=L->length) return 0;ElemType* p=&(L->elem[i-1]);e=*p;ElemType* q=&(L->elem[L->length-1]);for(p++;p<=q;p++) *(p-1)=*p;L->length--;return e;
}//顺序表合并
sqList mergeList(sqList* L1,sqList* L2,sqList L)
{ElemType* pa=L1->elem,*pb=L2->elem;L.length=L1->length+L2->length;L.listsize=L.length;L.elem=(ElemType*)malloc(INIT_SIZE*sizeof(ElemType));ElemType* pc=L.elem;if(!L.elem) exit(1);ElemType* last1=L1->elem[L1->length-1];ElemType* last2=L2->elem[L2->length-1];while(pa<=last1&&pb<=last2){if(*pa<=*pb) *pc++ =*pa++;else *pc++ =*pb++;}while(pa<=last1) *pc++=*pa++;while(pb<=last2) *pc++=*pb++;return L;
}

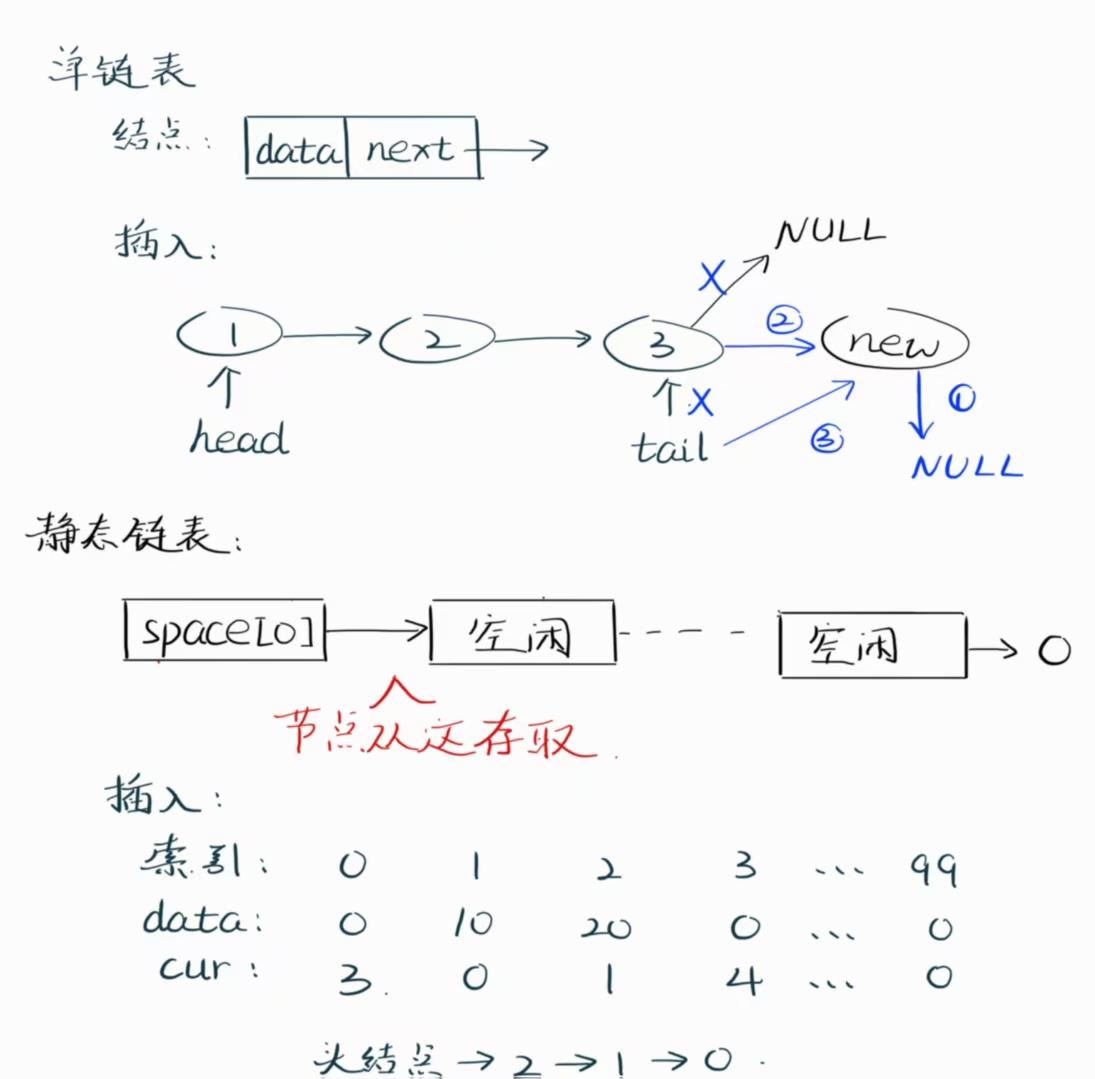
3. 线性表的链式存储又叫做单链表。链表的存储从头结点开始，头指针指向链表的第一节结点，若线性表为空表则头指针为NULL。单链表是非随机存取的存储结构。

#include<stdio.h>
#include<stdlib.h>  // 添加malloc和exit需要的头文件//typedef int ET;
//这样定义方便我们对程序的维护，为了方便后面还是用inttypedef struct Node
{int data;struct Node* next;
}Node;//头结点指向第一个结点，尾结点指向最后一个结点
//前者一般为必选项
typedef struct
{Node* head,*tail;int len;
}linkList;//创建结点
Node* createNode(int e)
{Node* newNode=(Node*)malloc(sizeof(Node));if(!newNode) exit(1);newNode->data=e;newNode->next=NULL;return newNode;
}//为什么需要指针，有一个原因是c里面没有引用传递
//这里的头结点实际是第一个结点，相当于“不带头结点的链表”
void insertend(linkList* L, int data) 
{Node* newNode=createNode(data);if(L->head==NULL){L->head=newNode;L->tail=newNode;}else{L->tail->next=newNode;L->tail=newNode;    //根据定义这里已经隐含了tail->next为NULL}L->len++;
}linkList createList(int n)
{linkList L;L.head = NULL;L.tail = NULL;L.len = 0;for(int i=0;i<n;i++){int temp;scanf("%d",&temp);insertend(&L,temp);}return L;
}//第k个结点后插入
void insertk(int k, linkList* L, int data)
{if(k<0||k>L->len) return;Node* newNode=createNode(data);if(k==0){newNode->next=L->head;L->head=newNode;if(L->len == 0) L->tail = newNode;  // 如果原来是空链表，更新tailL->len++;return;}if(k == L->len){insertend(L, data);return;}Node* current=L->head;  //用一个新指针指向头结点指向的位置，这样后续对指针的更新不会影响原有的头结点for(int i=0;i<k-1;i++) current=current->next;newNode->next=current->next;current->next=newNode;L->len++;
}//删除第k个结点
void deletek(int k, linkList* L)
{if(k<1||k>=L->len) return;if(k==1){Node* temp=L->head;L->head=L->head->next;if(L->len == 1) L->tail = NULL;  // 如果删除后链表为空，更新tailfree(temp);L->len--;return;}Node* current=L->head;for(int i=1;i<k;i++) current=current->next; //最终指向前一个结点Node* temp=current->next;current->next=temp->next;if(k == L->len) L->tail = current;  // 如果删除的是尾节点，更新tailfree(temp);L->len--;
}void print(Node* head)
{Node* current=head;while(current!=NULL){printf("%d ",current->data);current=current->next;}printf("\n");
}void freelist(linkList* L)
{Node* current=L->head;while(current!=NULL){Node* temp=current;current=current->next;free(temp);}L->head=NULL;L->tail=NULL;L->len=0;
}

4. 在一些不设“指针”类型的高级语言中，比如Java，我们可以使用静态链表。就是开设一个一维数组，数组的零号位视为头结点，这里的头结点定义为其next指向第一个结点。

#include<stdio.h>
#include<stdlib.h>#define MAXSIZE 100
typedef struct {int data;int cur;    // 游标，相当于next
} Component, StaticList[MAXSIZE];// 初始化静态链表
// 索引0: 数据链表头, 索引1: 空闲链表头
void initList(StaticList space)
{space[0].cur = 0;        // 数据链表初始为空space[1].cur = 2;        // 空闲链表从2开始for(int i = 2; i < MAXSIZE - 1; i++){space[i].cur = i + 1;space[i].data = 0;}space[MAXSIZE - 1].cur = 0;  // 最后一个节点指向0
}// 分配空闲节点
int mallocList(StaticList space)
{int i = space[1].cur;    // 从空闲链表头取节点if (i != 0) {space[1].cur = space[i].cur;}return i;
}// 释放节点
void freeList(StaticList space, int k)
{space[k].cur = space[1].cur;space[1].cur = k;
}// 获取链表长度
int getLength(StaticList space)
{int len = 0;int k = space[0].cur;    // 从数据链表头开始while(k != 0){len++;k = space[k].cur;}return len;
}// 在位置i插入元素e（头插法）
void insertList(StaticList space, int i, int e)
{if(i < 1 || i > getLength(space) + 1) {printf("插入位置无效\n");return;}int k = mallocList(space);if(k == 0) {printf("空间已满，无法插入\n");return;}space[k].data = e;// 找到插入位置的前一个节点int j = 0;  // 数据链表头for(int l = 1; l < i; l++) {j = space[j].cur;}// 插入节点space[k].cur = space[j].cur;space[j].cur = k;
}// 删除位置i的元素
int deleteList(StaticList space, int i)
{if(i < 1 || i > getLength(space)) {printf("删除位置无效\n");return -1;}// 找到要删除节点的前一个节点int j = 0;  // 数据链表头for(int l = 1; l < i; l++) {j = space[j].cur;}int k = space[j].cur;    // 要删除的节点int e = space[k].data;space[j].cur = space[k].cur;  // 从链表中移除freeList(space, k);      // 释放节点return e;
}// 打印数据链表
void printList(StaticList space)
{int k = space[0].cur;    // 从数据链表头开始if(k == 0){printf("链表为空");return;}while(k != 0){printf("%d ", space[k].data);k = space[k].cur;}
}// 打印空闲链表（调试用）
void printFreeList(StaticList space)
{printf("空闲节点: ");int k = space[1].cur;    // 从空闲链表头开始while(k != 0){printf("[%d] ", k);k = space[k].cur;}printf("\n");
}// 静态链表求差集：L1 - L2
void differenceList(StaticList space1, StaticList space2, StaticList result)
{// 初始化结果链表initList(result);// 遍历L1的所有元素int p1 = space1[0].cur;  // L1的第一个数据节点while(p1 != 0){int data1 = space1[p1].data;int found = 0;// 在L2中查找当前元素int p2 = space2[0].cur;  // L2的第一个数据节点while(p2 != 0){if(space2[p2].data == data1){found = 1;break;}p2 = space2[p2].cur;}// 如果没在L2中找到，则加入差集if(!found){// 分配新节点int k = mallocList(result);if(k == 0) {printf("结果链表空间不足\n");return;}result[k].data = data1;// 插入到结果链表尾部int j = 0;  // 结果链表的头while(result[j].cur != 0) {j = result[j].cur;}result[k].cur = 0;      // 新节点作为尾节点result[j].cur = k;      // 原尾节点指向新节点}p1 = space1[p1].cur;}
}

5. 双向链表:除了next，还有个pre。这里的头节点衔接了第一个结点和最后一个结点

#include <stdio.h>
#include <stdlib.h>typedef int DataType;
typedef struct LinkedNode{DataType data;struct LinkedNode *prev;struct LinkedNode *next;
}LinkedNode;typedef struct LinkedList{int length;LinkedNode head;
}LinkedList;void init_list(LinkedList *list)
{list->length=0;list->head.prev=&list->head;list->head.next = &list->head;
}LinkedNode *alloc_node(DataType data)
{LinkedNode *node = (LinkedNode*)malloc(sizeof(LinkedNode));if (node == NULL) exit(1);node->data = data;node->prev = NULL;node->next = NULL;return node;
}void push_front(LinkedList *list, DataType data)
{LinkedNode *newNode = alloc_node(data);LinkedNode *first = list->head.next;newNode->prev = &list->head;newNode->next = first;first->prev = newNode;list->head.next = newNode;list->length++;
}void push_back(LinkedList *list, DataType data)
{LinkedNode *newNode = alloc_node(data);LinkedNode *last = list->head.prev;newNode->prev = last;newNode->next = &list->head;last->next = newNode;list->head.prev = newNode;list->length++;
}void traverse(LinkedList *list)
{LinkedNode *current = list->head.next;int isFirst = 1;while (current != &list->head){if (!isFirst){printf(" ");}printf("%d", current->data);isFirst = 0;current = current->next;}printf("\n");
}void traverse_back(LinkedList *list)
{LinkedNode *current = list->head.prev;int isFirst = 1;while (current != &list->head) {if (!isFirst) {printf(" ");}printf("%d", current->data);isFirst = 0;current = current->prev;}printf("\n");
}void free_list(LinkedList *list)
{LinkedNode *current = list->head.next;while (current != &list->head){LinkedNode *temp = current;current = current->next;free(temp);}list->length = 0;list->head.prev = &list->head;list->head.next = &list->head;
}

题目1.两个有序单链表求差集

各依次输入递增有序若干个不超过100的整数，分别建立两个递增有序单链表，分别表示集合A和集合B。设计算法求出两个集合A和B 的差集（即仅由在A中出现而不在B中出现的元素所构成的集合），并存放于A链表中。要求结果链表仍使用原来两个链表的存储空间, 不另外占用其它的存储空间。然后输出求的差集的单链表。

Node* compareList(Node* A, Node* B)
{Node* temp = createNode(0), *curA = A, *curB = B;temp->next = A;           // 创建临时头节点Node* last = temp;        // 记录前驱节点while(curA != NULL && curB != NULL){if(curA->data > curB->data) curB = curB->next;        // B指针前进else if(curA->data < curB->data){last = curA;              // 更新前驱curA = curA->next;        // A指针前进}else  // curA->data == curB->data{last->next = curA->next;  // 从A中删除当前节点free(curA);curA = last->next;        // A指针移动到下一个curB = curB->next;        // B指针前进}}Node* newHead = temp->next;free(temp);return newHead;
}

题目2：有序链表的归并

建立两个有序的单链表，将这两个有序单链表合并成为一个有序单链表，并依次输出合并后的单链表数据。

Node* integralList(Node* A, Node* B)
{Node dummy;           // 创建虚拟头节点（在栈上，不需要malloc）Node* tail = &dummy;  // 尾指针，指向当前合并链表的尾部dummy.next = NULL;    // 初始化虚拟头节点// 比较两个链表的当前节点，选择较小的加入结果链表while (A != NULL && B != NULL){if (A->data <= B->data){tail->next = A;  // 将A的当前节点连接到结果链表A = A->next;     // A指针前进}else{tail->next = B;  // 将B的当前节点连接到结果链表B = B->next;     // B指针前进}tail = tail->next;   // 尾指针前进}// 处理剩余节点if (A != NULL) tail->next = A;if (B != NULL) tail->next = B;return dummy.next;  // 返回合并后的链表头
}

题目3：链表去重

给定一个带整数键值的链表 L，你需要把其中绝对值重复的键值结点删掉。即对每个键值 K，只有第一个绝对值等于 K 的结点被保留。同时，所有被删除的结点须被保存在另一个链表上。例如给定 L 为 21→-15→-15→-7→15，你需要输出去重后的链表 21→-15→-7，还有被删除的链表 -15→15。

输入格式：

输入在第一行给出 L 的第一个结点的地址和一个正整数 N（≤105，为结点总数）。一个结点的地址是非负的 5 位整数，空地址 NULL 用 -1 来表示。

随后 N 行，每行按以下格式描述一个结点：

地址 键值 下一个结点

其中地址是该结点的地址，键值是绝对值不超过104的整数，下一个结点是下个结点的地址。

输出格式：

首先输出去重后的链表，然后输出被删除的链表。每个结点占一行，按输入的格式输出。

输入样例：

00100 5
99999 -7 87654
23854 -15 00000
87654 15 -1
00000 -15 99999
00100 21 23854

输出样例：

00100 21 23854
23854 -15 99999
99999 -7 -1
00000 -15 87654
87654 15 -1

#include<stdio.h>
#include<stdlib.h>
#include<math.h>typedef struct Node
{int data;int next;
}Node;//用哈希表存储这种类静态链表更方便有木有
int main()
{Node map[100000];int head, N;scanf("%d %d", &head, &N);for(int i = 0; i < N; i++){int cur, data, next;scanf("%d %d %d", &cur, &data, &next);map[cur].data = data;map[cur].next = next;}int isExist[10001] = {0};int resultList[100000], deleteList[100000];int resCount = 0, delCount = 0;int cur = head;while(cur != -1){if(!isExist[abs(map[cur].data)]){isExist[abs(map[cur].data)] = 1;resultList[resCount++] = cur;}else{deleteList[delCount++] = cur;}cur = map[cur].next; }for(int i = 0; i < resCount; i++){int addr = resultList[i];if(i == resCount - 1){printf("%05d %d -1\n", addr, map[addr].data);}else{printf("%05d %d %05d\n", addr, map[addr].data, resultList[i+1]);}}for(int i = 0; i < delCount; i++){int addr = deleteList[i];if(i == delCount - 1){printf("%05d %d -1\n", addr, map[addr].data);}else{printf("%05d %d %05d\n", addr, map[addr].data, deleteList[i+1]);}}return 0;
}

题目4：逆序建立链表

输入一个整数n，再输入n个整数，按照输入的相反顺序建立单链表，并遍历所建立的单链表，输出这些数据。

输入格式:

测试数据有多组，处理到文件尾。每组测试输入一个整数n，再输入n个整数。

输出格式:

对于每组测试，输出结果链表中的各结点的数据域的值（数据之间留一个空格）。

#include<stdio.h>
#include<stdlib.h>typedef struct Node
{int data;struct Node* next;
}Node;Node* createNode(int data)
{Node* newNode=(Node*)malloc(sizeof(Node));if(newNode==NULL) exit(1);newNode->data=data;newNode->next=NULL;return newNode;
}void freeList(Node* head)
{Node* temp;while(head!=NULL){temp=head;head=head->next;free(temp);}
}Node* insert(Node* head,int data)
{Node* newNode=createNode(data);newNode->next=head;return newNode;
}void traverse(Node* head)
{Node* cur=head;int isFirst=1;while(cur!=NULL){if(!isFirst) printf(" ");isFirst=0;printf("%d",cur->data);cur=cur->next;}printf("\n");
}int main()
{int n,data;while(scanf("%d",&n)==1){Node* head=NULL;for(int i=0;i<n;i++){scanf("%d",&data);head=insert(head,data);}traverse(head);freeList(head);}return 0;
}

总结：

三、栈和队列

1. 栈和队列也是线性表

2. 栈属于后进先出，有栈底和栈顶，base栈底指针始终指向栈底的位置，如果base等于NULL则栈空。top则为栈顶指针，指向栈顶元素的下一个位置，所以top=base也可以是栈空的标志

#include<stdio.h>
#include<stdlib.h>
#include<string.h>typedef struct
{int* base;int* top;int stacksize;
}Stack;void initStack(Stack* s)
{s->base = (int*)malloc(50*sizeof(int));if(!s->base) exit(1);s->top = s->base;s->stacksize = 50;
}void push(Stack* s, int value)
{if(s->top - s->base >= s->stacksize){int current_size = s->top - s->base;  // 保存当前元素个数s->base = (int*)realloc(s->base, (s->stacksize + 50)*sizeof(int));if(!s->base) exit(1);s->top = s->base + current_size;      // 根据实际元素个数更新tops->stacksize += 50;}*s->top++ = value;
}int pop(Stack* s)
{if(s->top == s->base) {return -1;}return *--(s->top);
}void freeStack(Stack* s)
{free(s->base);s->base = NULL;s->top = NULL;s->stacksize = 0;
}

3. 上面那个是顺序栈，下面的是链式栈

结构类似：栈顶 → (20) → (10) → NULL

#include<stdio.h>
#include<stdlib.h>typedef struct Node
{int data;struct Node* next;
}Node;typedef struct
{Node* top;
}listStack;void initListStack(listStack* s)
{s->top=NULL;
}void push(listStack* s,int value)
{Node* newNode=(Node*)malloc(sizeof(Node));if(!newNode) exit(1);newNode->next=s->top;newNode->data=value;s->top=newNode;
}int pop(listStack* s)
{if(s->top==NULL){printf("错误：栈为空。\n");return -1;}Node* temp=s->top;s->top=s->top->next;int data=temp->data;free(temp);return data;
}

4.队列是先进先出，类似羽毛球桶。允许插入的是队尾，允许删除的是队头

顺序队列：

#define MAXSIZE 100
typedef struct {int data[MAXSIZE];int front;  // 队头指针int rear;   // 队尾指针
} SeqQueue;void initQueue(SeqQueue *Q) {Q->front = 0;Q->rear = 0;
}int enQueue(SeqQueue *Q, int e) {if(Q->rear == MAXSIZE) return 0;  // 队列满Q->data[Q->rear++] = e;return 1;
}int deQueue(SeqQueue *Q, int *e) {if(Q->front == Q->rear) return 0;  // 队列空*e = Q->data[Q->front++];return 1;
}

循环队列：

#define MAXSIZE 100
typedef struct {int data[MAXSIZE];int front;  // 队头指针int rear;   // 队尾指针
} CircularQueue;void initQueue(CircularQueue *Q) {Q->front = 0;Q->rear = 0;
}int enQueue(CircularQueue *Q, int e) {if((Q->rear + 1) % MAXSIZE == Q->front) return 0;  // 队列满Q->data[Q->rear] = e;Q->rear = (Q->rear + 1) % MAXSIZE;return 1;
}int deQueue(CircularQueue *Q, int *e) {if(Q->front == Q->rear) return 0;  // 队列空*e = Q->data[Q->front];Q->front = (Q->front + 1) % MAXSIZE;return 1;
}int queueLength(CircularQueue Q) {return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

链式存储：

typedef struct QNode {int data;struct QNode *next;
} QNode;typedef struct {QNode *front;  // 队头指针QNode *rear;   // 队尾指针
} LinkQueue;void initQueue(LinkQueue *Q) {Q->front = Q->rear = (QNode*)malloc(sizeof(QNode));if(!Q->front) exit(1);Q->front->next = NULL;
}void enQueue(LinkQueue *Q, int e) {QNode *p = (QNode*)malloc(sizeof(QNode));if(!p) exit(1);p->data = e;p->next = NULL;Q->rear->next = p;Q->rear = p;
}int deQueue(LinkQueue *Q, int *e) {if(Q->front == Q->rear) return 0;  // 队列空QNode *p = Q->front->next;*e = p->data;Q->front->next = p->next;if(Q->rear == p) Q->rear = Q->front;  // 如果删除的是最后一个元素free(p);return 1;
}

题目1：找出序列a的入栈出栈序列

输入序列为1,2,3,4...,n，判断通过一个栈能否得序列a, 且输出入栈和出栈过程。

输入格式:

每组输入为两行：

第1行是一个正整数n,1<=n<=100;

第2行是序列a，共有n个整数，表示要得到的目标序列。序列为1~n的排列，题目保证序列长度为n, 序列中的整数都不相同，且整数在区间[1,n]之内。

可有多组输入。

输出格式:

对于每组输入，先输出一行，如果能通过栈得到序列a, 则输出YES，并接着输出得到序列a的入栈出栈的操作。
如果无法得到序列a，只需要输出NO。

PS：这里是我认为瞪眼法最快的判断方法有cab出现就不可能，后面附上ds的标准解答

int hasInvalidPattern(int* target, int n)
{for(int i = 0; i < n; i++){for(int j = i + 1; j < n; j++){if(target[j] == target[i] - 2){for(int k = j + 1; k < n; k++){if(target[k] == target[i] - 1){return 1;}}}}}return 0;
}int main()
{int n;while(scanf("%d",&n)!=EOF){int target[n];for(int i=0;i<n;i++){int a;scanf("%d",&a);target[i]=a;}if(hasInvalidPattern(target, n)){printf("NO\n");continue;}else printf("YES\n");Stack s;initStack(&s);int cur=1;int index=0;while(index<n){if(getTop(s)==target[index]){printf("%s %d\n","pop",pop(&s));index++;}else{push(&s,cur);printf("%s %d\n","push",cur);cur++;}}}return 0;
}

以下是ds的算法：

while(还有元素要匹配)
{
if(栈顶 == 当前目标元素)
{
// 匹配成功，出栈并处理下一个目标元素
pop();
index++;
}
else if(还有数字可以入栈)
{
// 入栈下一个数字
push(cur);
cur++;
}
else
{
// 栈顶不匹配且没有数字可入了 → 非法序列
return 0;
}
}

// 更通用的栈序列合法性检查
int isValidStackSequence(int* target, int n)
{Stack s;initStack(&s);int cur = 1;int index = 0;while(index < n){if(getTop(s) == target[index]){pop(&s);index++;}else if(cur <= n){push(&s, cur);cur++;}else{freeStack(&s);return 0;  // 非法序列}}freeStack(&s);return 1;  // 合法序列
}

题目2：数值转换

void conversion(int N)
{Stack s;initStack(&s);int n;scanf("%d",&n);while(n){push(s,n%N);n/=N;}while(!emptyStack(s)){int e=pop(s);printf("%d",e);}
}

题目3：括号匹配

char pairs(char a) {if (a == '}') return '{';if (a == ']') return '[';if (a == ')') return '(';return 0;
}bool match()
{Stack s;initStack(&s);char tar[100];gets(tar);int i=strlen(tar);if(i%2==1) return 0;for(int j=0;j<i;j++){char ch=pairs(tar[j]);if(ch){if(top==base||s.top()!=ch) return 0;pop(&s);}else push(&s,tar[j]);}return 1;
}

四、串

1. 串值必须用一对单引号括起来，单引号本身不属于串

KMP算法：不回退主串上的指针
关键在于先求出待匹配子串的next数组
next数组存储的是跳过字串的字符数
本质是寻找字串中相同前后缀的长度

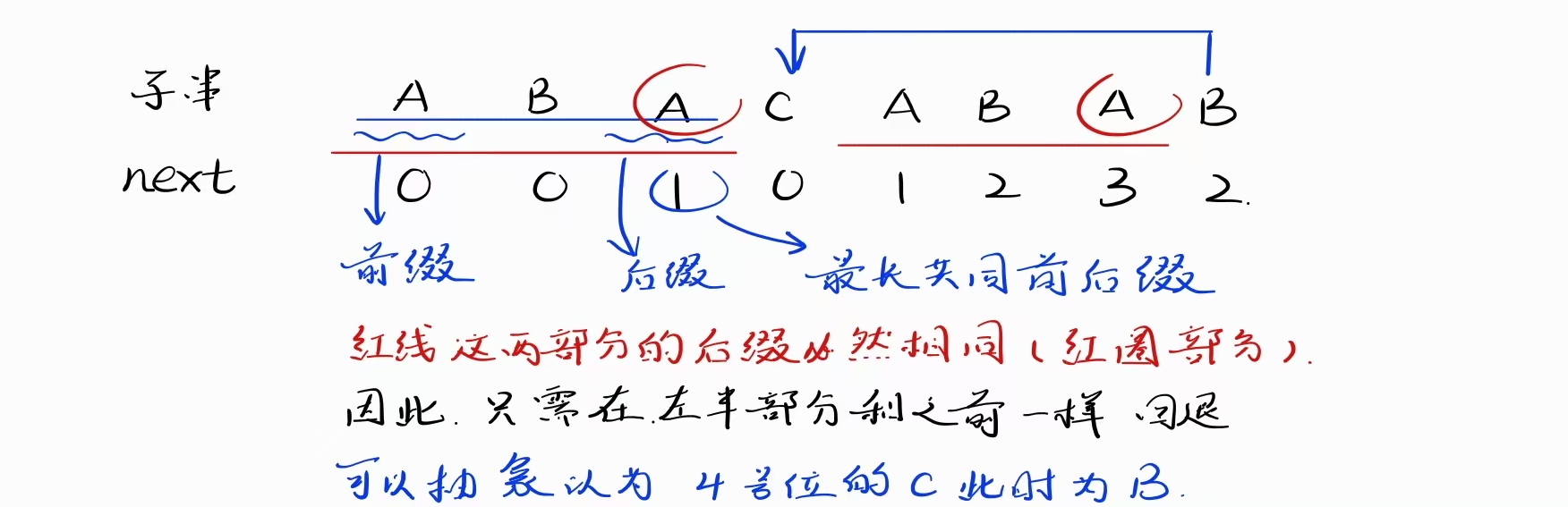
int* build_next(const char* patt) {int len = strlen(patt);if (len == 0) {return NULL;}// 分配 next 数组内存int* next = (int*)malloc(len * sizeof(int));if (next == NULL) {return NULL;}next[0] = 0;  // next 数组第一个元素总是 0int prefix_len = 0;  // 当前共同前后缀的长度int i = 1;  // 从第二个字符开始while (i < len) {if (patt[prefix_len] == patt[i]) {prefix_len++;next[i] = prefix_len;i++;} else {if (prefix_len == 0) {next[i] = 0;i++;} else {prefix_len = next[prefix_len - 1];}}}return next;
}

题目一：删除字符串中的子串

输入2个字符串S1和S2，要求删除字符串S1中出现的所有子串S2，即结果字符串中不能包含S2。

输入格式：

输入在2行中分别给出不超过80个字符长度的、以回车结束的2个非空字符串，对应S1和S2。

输出格式：

在一行中输出删除字符串S1中出现的所有子串S2后的结果字符串。

输入样例：

Tomcat is a male ccatat
cat

输出样例：

Tom is a male

#include<stdio.h>
#include<stdlib.h>
#include<string.h>int main()
{char s1[1000];char s2[1000];char s3[1000];gets(s1);gets(s2);int len2=strlen(s2);if(len2==0){printf("%s",s1);return 0;}while(1){int len1=strlen(s1);int i=0,z=0;int found=0;while(i<=len1-len2){int isfound=1;for(int j=0,k=i;j<len2;j++,k++){if(s1[k]!=s2[j]){isfound=0;break;}}if(isfound){i+=len2;found=1;}else{s3[z++]=s1[i++];}}while(i<len1){s3[z++]=s1[i++];}s3[z]='\0';if(!found) break;strcpy(s1, s3);}printf("%s",s3);return 0;
}

题目二：约瑟夫问题

循环在限定范围内和时针一样理解，也就是求模

约瑟夫问题：有ｎ只猴子，按顺时针方向围成一圈选大王（编号从１到ｎ），从第１号开始报数，一直数到ｍ，数到ｍ的猴子退出圈外，剩下的猴子再接着从1 开始报数。就这样，直到圈内只剩下一只猴子时，这个猴子就是猴王，编程求输入ｎ，ｍ后，输出最后猴王的编号。

输入格式:

每行是用空格分开的两个整数，第一个是 n，第二个是m ( 0 < m, n < 300) 。最后一行是：0 0 。

输出格式:

对于每行输入数据（最后一行除外)，输出数据也是一行，即最后猴王的编号。

#include<stdio.h>
#include<stdlib.h>int* init(int n)
{int* a = (int*)malloc((n + 1) * sizeof(int));for(int i=0;i<n;i++){a[i]=i+1;}a[n] = -1;return a;
}int* del(int* a,int pos)
{int i=pos;for(;a[i]!=-1;i++){a[i]=a[i+1];}return a;
}int main()
{int n,m;int isfirst=1;while(1){   scanf("%d %d",&n,&m);if(n==0&&m==0) break;int* a=init(n);int len=n;int pos=0;while(len>1){pos=(pos+(m-1))%len;del(a,pos);len--;}if(isfirst){printf("%d",a[0]);isfirst=0;}else{printf("\n%d",a[0]);}free(a);}return 0;
}

五、数组和广义表

1. 在二维数组里，以行序为主序就是先把列存满，再换行，同理还有以列序为主序。如果是三维数组呢，同样也很好理解，其实就是先把二维平面的每一个位置的高放满，其他和二维数组类似。

2. 对于对称矩阵，可以压缩为n*(n+1)/2的一维数组，这里是包含有对角元的，注意在压缩矩阵里，是以0开始的，所以转换的时候记得减1。

对于三角矩阵，其压缩矩阵是不包含对角元的

3. 最关键的还有稀疏矩阵，对于稀疏矩阵，我们考虑用三元组表来存储，注意，还需要有一组行列值来保证原矩阵的大小正确

先进行一些基本的定义环节，这里的rpos是为了去确定每一行的第一个元素在整个压缩一维数组里的相对位置，同时需要注意，为了方便逻辑理解，把一维数组的第一个位置空置，符合自然的下标定义，不会搞混

#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 12500  // 假设非零元个数的最大值为12500
#define OK 1
#define ERROR 0typedef int Status;
typedef int ElemType;// 三元组结构
typedef struct {int i, j;    // 该非零元的行下标和列下标ElemType e;  // 非零元的值
} Triple;// 三元组顺序表
typedef struct {Triple data[MAXSIZE + 1];  // 非零元三元组表，data[0]未用int mu, nu, tu;            // 矩阵的行数、列数和非零元个数
} TSMatrix;// 行逻辑链接顺序表
typedef struct {Triple data[MAXSIZE + 1];  // 非零元三元组表int rpos[MAXSIZE + 1];     // 各行第一个非零元的位置int mu, nu, tu;            // 矩阵的行数、列数和非零元个数
} RLSMatrix;

转置矩阵的一个难点就是在于两个矩阵之间的元素相对位置的一个变换，为此在普通的矩阵转置中，我们可以对原矩阵按列为主序搜索，这也就相当于对转置矩阵按行为主序进行放置

// 简单转置算法
Status TransposeSMatrix(TSMatrix M, TSMatrix *T) {// 采用三元组表存储表示，求稀疏矩阵M的转置矩阵Tint p, q, col;T->mu = M.nu;T->nu = M.mu;T->tu = M.tu;if (T->tu) {q = 1;  // q用于T->data的当前存储位置for (col = 1; col <= M.nu; ++col) {for (p = 1; p <= M.tu; ++p) {if (M.data[p].j == col) {T->data[q].i = M.data[p].j;T->data[q].j = M.data[p].i;T->data[q].e = M.data[p].e;++q;}}}}return OK;
}

前面定义中涉及的行逻辑链接顺序表，与快速转置的原理类似，在快速转置中，我们可以先计算出原矩阵每一列的第一个未处理元素在转置后矩阵的相对位置

使用辅助向量优化：
num[col]：矩阵M中第col列的非零元个数
cpot[col]：M中第col列第一个非零元在转置矩阵中的位置
cpot[1] = 1
cpot[col] = cpot[col-1] + num[col-1] (2 ≤ col ≤ nu)

//快速转置算法
Status FastTransposeSMatrix(TSMatrix M, TSMatrix *T) {// 采用三元组表存储表示，求稀疏矩阵M的转置矩阵Tint col, t, p, q;int num[M.nu + 1], cpot[M.nu + 1];T->mu = M.nu;T->nu = M.mu;T->tu = M.tu;if (T->tu) {// 初始化num数组for (col = 1; col <= M.nu; ++col) {num[col] = 0;}// 求M中每一列含非零元个数for (t = 1; t <= M.tu; ++t) {++num[M.data[t].j];}// 求第col列中第一个非零元在T->data中的位置cpot[1] = 1;for (col = 2; col <= M.nu; ++col) {cpot[col] = cpot[col - 1] + num[col - 1];}// 进行转置for (p = 1; p <= M.tu; ++p) {col = M.data[p].j;q = cpot[col];T->data[q].i = M.data[p].j;T->data[q].j = M.data[p].i;T->data[q].e = M.data[p].e;++cpot[col];}}return OK;
}

矩阵乘法应用也是相当的广泛的，根据必备的线性代数知识，只有左矩阵的列数等于右矩阵的行数才能够相乘，最后得到的结果矩阵行数应该等于左矩阵行数，列数应该等于右矩阵列数

for (i = 1; i <= m1; ++i)for (j = 1; j <= n2; ++j) {Q[i][j] = 0;for (k = 1; k <= n1; ++k)Q[i][j] += M[i][k] * N[k][j];}
// 时间复杂度：O(m1 × n1 × n2)

对于稀疏矩阵来说其实可以提高这个效率，简单概括算法思路：
遍历左矩阵的每一行 arow
设置一个累加器数组去保存当前行结果矩阵的各列答案 temp[ccol]
不要忘了先去更新一下当前行的rpos[arow]
遍历当前行的每一个非零元
找到符合条件的 brow=acol
遍历符合条件的这一行的每一个非零元
进行计算储存到temp[ccol]
对遍历结果数组的每一列，对非零结果的列值进行压缩存储

// 稀疏矩阵乘法
Status MultiSMatrix(RLSMatrix M, RLSMatrix N, RLSMatrix *Q) {// 求矩阵乘积Q=M×N，采用行逻辑链接存储表示int arow, brow, p, q, t, tp;int ccol;int ctemp[N.nu + 1];  // 累加器if (M.nu != N.mu) {return ERROR;  // 矩阵乘法条件不满足}// 初始化QQ->mu = M.mu;Q->nu = N.nu;Q->tu = 0;// 如果M或N是零矩阵，则Q也是零矩阵if (M.tu * N.tu == 0) {return OK;}// 处理M的每一行for (arow = 1; arow <= M.mu; ++arow) {// 当前行各元素累加器清零for (ccol = 1; ccol <= Q->nu; ++ccol) {ctemp[ccol] = 0;}// 设置Q中当前行的起始位置Q->rpos[arow] = Q->tu + 1;// 确定M中当前行的元素范围if (arow < M.mu) {tp = M.rpos[arow + 1];} else {tp = M.tu + 1;}// 对M当前行中每一个非零元for (p = M.rpos[arow]; p < tp; ++p) {brow = M.data[p].j;  // 找到对应元在N中的行号// 确定N中brow行的元素范围if (brow < N.mu) {t = N.rpos[brow + 1];} else {t = N.tu + 1;}// 对N中brow行的每一个非零元for (q = N.rpos[brow]; q < t; ++q) {ccol = N.data[q].j;  // 乘积元素在Q中列号ctemp[ccol] += M.data[p].e * N.data[q].e;} // for q} // for p，求得Q中第arow行的非零元// 压缩存储该行非零元for (ccol = 1; ccol <= Q->nu; ++ccol) {if (ctemp[ccol]) {if (++(Q->tu) > MAXSIZE) {return ERROR;}Q->data[Q->tu].i = arow;Q->data[Q->tu].j = ccol;Q->data[Q->tu].e = ctemp[ccol];}} // for ccol} // for arowreturn OK;
}

4. 十字链表

#include <stdio.h>
#include <stdlib.h>#define Status int
#define OK 1
#define OVERFLOW -1
#define ElemType int  // 假设矩阵元素类型为整型// 数据结构定义
typedef struct OLNode {int i, j;ElemType e;struct OLNode *right, *down;
} OLNode, *OLink;typedef struct {OLink *rhead, *chead;int mu, nu, tu;
} CrossList;// 创建稀疏矩阵的十字链表
Status CreateSMatrix_OL(CrossList *M) {int n, m, t, i, j, e;OLink p, q;// 输入矩阵的基本信息printf("请输入矩阵的行数、列数和非零元个数: ");scanf("%d %d %d", &m, &n, &t);M->mu = m;M->nu = n;M->tu = t;// 分配行头指针数组if (!(M->rhead = (OLink *)malloc((m + 1) * sizeof(OLink)))) exit(OVERFLOW);// 分配列头指针数组if (!(M->chead = (OLink *)malloc((n + 1) * sizeof(OLink)))) exit(OVERFLOW);// 初始化行列头指针为NULLfor (int idx = 1; idx <= m; idx++) M->rhead[idx] = NULL;for (int idx = 1; idx <= n; idx++) M->chead[idx] = NULL;// 输入非零元并建立十字链表printf("请按任意顺序输入%d个非零元(行 列 值)，以0 0 0结束:\n", t);for (int k = 0; k < t; k++) {scanf("%d %d %d", &i, &j, &e);if (i == 0 && j == 0 && e == 0) break;// 创建新节点if (!(p = (OLNode *)malloc(sizeof(OLNode)))) exit(OVERFLOW);p->i = i;p->j = j;p->e = e;p->right = NULL;p->down = NULL;// 插入到行链表（按列号升序）if (M->rhead[i] == NULL || M->rhead[i]->j > j) {// 插入到行首p->right = M->rhead[i];M->rhead[i] = p;} else {// 寻找在行表中的插入位置for (q = M->rhead[i]; q->right && q->right->j < j; q = q->right);p->right = q->right;q->right = p;}// 插入到列链表（按行号升序）if (M->chead[j] == NULL || M->chead[j]->i > i) {// 插入到列首p->down = M->chead[j];M->chead[j] = p;} else {// 寻找在列表中的插入位置for (q = M->chead[j]; q->down && q->down->i < i; q = q->down);p->down = q->down;q->down = p;}}return OK;
}

5. 广义表lists，与表list做区分

广义表是可以嵌套的，所以广义表里面储存的既可以是元素，也可以是广义表

广义表的长度就是广义表存储的原子和子表的个数

广义表的深度就是广义表中括号的最大层数

对于非空的广义表来说，表头就是第一个元素，不管是原子还是子表，那对于表尾呢，表尾是除了广义表表头之外，剩下的元素组成的表，没错，表尾是一个表

六、树和二叉树

1. 树结点：包含一个数据元素和若干指向其子树的分支。

结点的度：结点拥有的子树数。树的度是各节点度的最大值

结点的层次从根开始定义，根为第一层。树中结点的最大层次称为树的深度

2. 二叉树：度不超过2。二叉树有五种基本形态

满二叉树：每一层都是满的二叉树

完全二叉树：结点是从上到下，从左到右以此排列的，中间没有缺少结点

问到n结点可以构造多少种二叉树时，可以运用卡塔兰数 $C_n = \frac{(2n)!}{(n+1)! \cdot n!}$

二叉树的性质：
1. 第i层最多2的(i-1)次方个结点
2. 深度为k的二叉树最多2的k次方-1个结点
3. 设n0为叶子结点数，n2为度为2的结点数，有n0=n2+1
4. n结点的完全二叉树的深度为[log2(n)]+1

3. 对于二叉树的存储我们一般采用链式存储。有二叉链表和三叉链表，三叉链表可以指向双亲结点。n结点二叉链表有n+1个空链域（也很好思考，原本一共2n个链域，除了根节点其他每个结点入度都为1，所以有n-1个链域被使用）

这里的visit函数是指遍历每一个结点要做什么，便于代码的复用
函数名本身就是一个指针
参数列表里之所以用函数指针，是因为需要一个指针变量，去指向不同功能的函数地址，在函数体内部直接使用visit就好了

typedef int Status;
#define OK 1
#define ERROR 0
#define OVERFLOW -1// 元素类型定义
typedef char TElemType;// 二叉树的二叉链表存储表示
typedef struct BiTNode {TElemType data;struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;// 队列结构用于层序遍历
typedef struct QueueNode {BiTree data;struct QueueNode *next;
} QueueNode;typedef struct {QueueNode *front;QueueNode *rear;
} LinkQueue;

// 创建二叉树（先序次序）
//    存字符，有空值
Status CreateBiTree(BiTree *T) {TElemType ch;// 从输入读取字符ch = getchar();// 如果是空格，表示空树if (ch == ' ') {*T = NULL;} else {// 创建新节点*T = (BiTree)malloc(sizeof(BiTNode));if (!*T) {return OVERFLOW;}// 赋值并递归创建左右子树(*T)->data = ch;CreateBiTree(&(*T)->lchild);  // 创建左子树CreateBiTree(&(*T)->rchild);  // 创建右子树}return OK;
}// 先序遍历
Status PreOrderTraverse(BiTree T, Status (*Visit)(TElemType e)) {if (T) {if (Visit(T->data)) {if (PreOrderTraverse(T->lchild, Visit)) {if (PreOrderTraverse(T->rchild, Visit)) {return OK;}}}return ERROR;}return OK;
}// 中序遍历
Status InOrderTraverse(BiTree T, Status (*Visit)(TElemType e)) {if (T) {if (InOrderTraverse(T->lchild, Visit)) {if (Visit(T->data)) {if (InOrderTraverse(T->rchild, Visit)) {return OK;}}}return ERROR;}return OK;
}// 后序遍历
Status PostOrderTraverse(BiTree T, Status (*Visit)(TElemType e)) {if (T) {if (PostOrderTraverse(T->lchild, Visit)) {if (PostOrderTraverse(T->rchild, Visit)) {if (Visit(T->data)) {return OK;}}}return ERROR;}return OK;
}// 层序遍历  (树里的BFS)
Status LevelOrderTraverse(BiTree T, Status (*Visit)(TElemType e)) {LinkQueue Q;BiTree p;if (!T) return OK;InitQueue(&Q);EnQueue(&Q, T);while (!QueueEmpty(Q)) {DeQueue(&Q, &p);if (!Visit(p->data)) {return ERROR;}if (p->lchild) {EnQueue(&Q, p->lchild);}if (p->rchild) {EnQueue(&Q, p->rchild);}}return OK;
}// 销毁二叉树
Status DestroyBiTree(BiTree *T) {if (*T) {if ((*T)->lchild) {DestroyBiTree(&(*T)->lchild);}if ((*T)->rchild) {DestroyBiTree(&(*T)->rchild);}free(*T);*T = NULL;}return OK;
}// 队列初始化
Status InitQueue(LinkQueue *Q) {Q->front = Q->rear = (QueueNode*)malloc(sizeof(QueueNode));if (!Q->front) return OVERFLOW;Q->front->next = NULL;return OK;
}// 入队
Status EnQueue(LinkQueue *Q, BiTree elem) {QueueNode *p = (QueueNode*)malloc(sizeof(QueueNode));if (!p) return OVERFLOW;p->data = elem;p->next = NULL;Q->rear->next = p;Q->rear = p;return OK;
}// 出队
Status DeQueue(LinkQueue *Q, BiTree *elem) {if (Q->front == Q->rear) return ERROR;QueueNode *p = Q->front->next;*elem = p->data;Q->front->next = p->next;if (Q->rear == p) {Q->rear = Q->front;}free(p);return OK;
}// 判断队列是否为空
Status QueueEmpty(LinkQueue Q) {return Q.front == Q.rear;
}

4. 线索二叉树：就是利用n+1个空链域，在遍历的过程中，找到这些结点的前驱或者后继，把这些空链域叫做线索，所以线索是指针，为了区别线索和左右孩子，增设tag区别

5. 中序找前驱和后继都很方便，先序二叉树无法有效找前驱，后序二叉树无法有效找后驱，因为要依托于父结点，而不改变的原有树结构的情况下是做不到直接找到父结点的。

6. 线索二叉树的主要优点是：

在不使用栈或递归的情况下，能够较快地找到某个遍历次序下的前驱和后继结点。
方便从任一结点出发遍历整棵树。
但是，后序线索二叉树的遍历仍然需要栈的支持

题目一：顺序存储的二叉树的遍历（创建虚拟栈）

对顺序存储方式存放的二叉树，给出前序、中序和后序遍历的非递归算法实现。

函数接口定义：

void PreOrder(BinaryTree tree);
void InOrder(BinaryTree tree);
void PostOrder(BinaryTree tree);

其中 BinaryTree 相关的数据类型的定义如下：

typedef char TElemSet; /* 树结点元素为单个字符 */
#define NIL '-'        /* 表示空指针的字符 */
typedef struct BinaryTreeNode *BinaryTree;
struct BinaryTreeNode {TElemSet *data; /* 数据元素顺序表 */int size;       /* 顺序表长度 */
};

三个遍历函数中，对结点的访问定义为输出该结点中存储的字符，前后无空格。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>typedef char TElemSet; /* 树结点元素为单个字符 */
#define NIL '-' /* 表示空指针的字符 */
typedef struct BinaryTreeNode *BinaryTree;
struct BinaryTreeNode {TElemSet *data; /* 数据元素顺序表 */int size;       /* 顺序表长度 */
};void PreOrder(BinaryTree tree);
void InOrder(BinaryTree tree);
void PostOrder(BinaryTree tree);int main(void)
{BinaryTree tree;int n, i; scanf("%d\n", &n);tree = (BinaryTree)malloc(sizeof(struct BinaryTreeNode));tree->data = (char *)malloc(sizeof(char) * (n+1));tree->size = n;tree->data[0] = NIL;for (i=1; i<=n; i++) {scanf("%c", &tree->data[i]);}PreOrder(tree);printf("\n");InOrder(tree);printf("\n");PostOrder(tree);printf("\n");return 0;
}
/* 你的代码将被嵌在这里 */

输入样例：

13
ABC-DE------F

输出样例：

ABDCEF
BDAEFC
DBFECA

typedef struct {int* indices;  // 存储节点索引int* visited;  // 用于后序遍历标记节点是否已访问（1表示已访问，0表示未访问）int top;       // 栈顶指针int capacity;  // 栈容量
} Stack;// 初始化栈
Stack* initStack(int capacity) {Stack* stack = (Stack*)malloc(sizeof(Stack));stack->capacity = capacity;stack->indices = (int*)malloc(sizeof(int) * capacity);stack->visited = (int*)malloc(sizeof(int) * capacity);stack->top = -1;return stack;
}// 入栈操作
void push(Stack* stack, int index, int visit) {if (stack->top < stack->capacity - 1) {stack->top++;stack->indices[stack->top] = index;stack->visited[stack->top] = visit;}
}// 出栈操作
void pop(Stack* stack, int* index, int* visit) {if (stack->top >= 0) {*index = stack->indices[stack->top];*visit = stack->visited[stack->top];stack->top--;}
}// 检查栈是否为空
int isEmpty(Stack* stack) {return stack->top == -1;
}// 释放栈内存
void freeStack(Stack* stack) {free(stack->indices);free(stack->visited);free(stack);
}// 前序遍历：根→左→右
void PreOrder(BinaryTree tree) {if (tree == NULL || tree->size < 1 || tree->data[1] == NIL) {return;}Stack* stack = initStack(tree->size);push(stack, 1, 0);  // 从根节点（索引1）开始while (!isEmpty(stack)) {int index, visit;pop(stack, &index, &visit);if (tree->data[index] == NIL) {continue;}// 访问当前节点printf("%c", tree->data[index]);// 右孩子入栈（后访问）int right = 2 * index + 1;if (right <= tree->size) {push(stack, right, 0);}// 左孩子入栈（先访问）int left = 2 * index;if (left <= tree->size) {push(stack, left, 0);}}freeStack(stack);
}// 中序遍历：左→根→右
void InOrder(BinaryTree tree) {if (tree == NULL || tree->size < 1 || tree->data[1] == NIL) {return;}Stack* stack = initStack(tree->size);int current = 1;  // 从根节点（索引1）开始while (current <= tree->size || !isEmpty(stack)) {// 遍历到最左孩子while (current <= tree->size && tree->data[current] != NIL) {push(stack, current, 0);current = 2 * current;  // 移动到左孩子}if (isEmpty(stack)) {break;}// 弹出并访问节点int index, visit;pop(stack, &index, &visit);printf("%c", tree->data[index]);// 处理右孩子current = 2 * index + 1;}freeStack(stack);
}// 后序遍历：左→右→根
void PostOrder(BinaryTree tree) {if (tree == NULL || tree->size < 1 || tree->data[1] == NIL) {return;}Stack* stack = initStack(tree->size);push(stack, 1, 0);  // 初始压入根节点，标记为未访问while (!isEmpty(stack)) {int index, visited;pop(stack, &index, &visited);if (tree->data[index] == NIL) {continue;}if (visited) {// 已访问过，输出节点值printf("%c", tree->data[index]);} else {// 未访问过，重新压入并标记为已访问push(stack, index, 1);// 压入右孩子（未访问）int right = 2 * index + 1;if (right <= tree->size) {push(stack, right, 0);}// 压入左孩子（未访问）int left = 2 * index;if (left <= tree->size) {push(stack, left, 0);}}}freeStack(stack);
}

题目二：前序+中序、后序+中序重建二叉树（跳过空值，存字符串）

前序+后序是无法重建二叉树的
这里用双指针原因有很多，可以认为是便于区分结点的输入值的边界，同时算术移动时会按结点数移动，不是字符数移动（如果需要存储的结点值是字符串的话）

前序+中序：

// 初始化静态链表
// 索引0: 数据链表头, 索引1: 空闲链表头
void initList(StaticList space)
{space[0].cur = 0;        // 数据链表初始为空space[1].cur = 2;        // 空闲链表从2开始for(int i = 2; i < MAXSIZE - 1; i++){space[i].cur = i + 1;space[i].data = 0;}space[MAXSIZE - 1].cur = 0;  // 最后一个节点指向0
}// 分配空闲节点
int mallocList(StaticList space)
{int i = space[1].cur;    // 从空闲链表头取节点if (i != 0) {space[1].cur = space[i].cur;}return i;
}// 释放节点
void freeList(StaticList space, int k)
{space[k].cur = space[1].cur;space[1].cur = k;
}// 获取链表长度
int getLength(StaticList space)
{int len = 0;int k = space[0].cur;    // 从数据链表头开始while(k != 0){len++;k = space[k].cur;}return len;
}// 在位置i插入元素e（头插法）
void insertList(StaticList space, int i, int e)
{if(i < 1 || i > getLength(space) + 1) {printf("插入位置无效\n");return;}int k = mallocList(space);if(k == 0) {printf("空间已满，无法插入\n");return;}space[k].data = e;// 找到插入位置的前一个节点int j = 0;  // 数据链表头for(int l = 1; l < i; l++) {j = space[j].cur;}// 插入节点space[k].cur = space[j].cur;space[j].cur = k;
}// 删除位置i的元素
int deleteList(StaticList space, int i)
{if(i < 1 || i > getLength(space)) {printf("删除位置无效\n");return -1;}// 找到要删除节点的前一个节点int j = 0;  // 数据链表头for(int l = 1; l < i; l++) {j = space[j].cur;}int k = space[j].cur;    // 要删除的节点int e = space[k].data;space[j].cur = space[k].cur;  // 从链表中移除freeList(space, k);      // 释放节点return e;
}// 打印数据链表
void printList(StaticList space)
{int k = space[0].cur;    // 从数据链表头开始if(k == 0){printf("链表为空");return;}while(k != 0){printf("%d ", space[k].data);k = space[k].cur;}
}// 打印空闲链表（调试用）
void printFreeList(StaticList space)
{printf("空闲节点: ");int k = space[1].cur;    // 从空闲链表头开始while(k != 0){printf("[%d] ", k);k = space[k].cur;}printf("\n");
}// 静态链表求差集：L1 - L2
void differenceList(StaticList space1, StaticList space2, StaticList result)
{// 初始化结果链表initList(result);// 遍历L1的所有元素int p1 = space1[0].cur;  // L1的第一个数据节点while(p1 != 0){int data1 = space1[p1].data;int found = 0;// 在L2中查找当前元素int p2 = space2[0].cur;  // L2的第一个数据节点while(p2 != 0){if(space2[p2].data == data1){found = 1;break;}p2 = space2[p2].cur;}// 如果没在L2中找到，则加入差集if(!found){// 分配新节点int k = mallocList(result);if(k == 0) {printf("结果链表空间不足\n");return;}result[k].data = data1;// 插入到结果链表尾部int j = 0;  // 结果链表的头while(result[j].cur != 0) {j = result[j].cur;}result[k].cur = 0;      // 新节点作为尾节点result[j].cur = k;      // 原尾节点指向新节点}p1 = space1[p1].cur;}
}

后序+中序：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef struct TreeNode {char val[10];struct TreeNode* left;struct TreeNode* right;
} TreeNode;// 在中序数组中找到目标值的位置
int findIndex(char** in_order, int len, char* target) {for (int i = 0; i < len; i++) {if (strcmp(in_order[i], target) == 0) {return i;}}return -1;
}// 根据后序和中序重建二叉树
TreeNode* buildTreeFromPostIn(char** post_order, int post_len, char** in_order, int in_len) {// 基准情况：如果数组为空，返回NULLif (post_len <= 0 || in_len <= 0) {return NULL;}// 步骤1：后序的最后一个元素是根节点// post_order: [左子树, 右子树, 根]char* root_val = post_order[post_len - 1];  // 取最后一个元素作为根节点TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));strcpy(root->val, root_val);root->left = NULL;root->right = NULL;// 步骤2：在中序数组中找到根节点的位置// in_order: [左子树, 根, 右子树]int root_idx = findIndex(in_order, in_len, root_val);// 步骤3：计算左右子树的大小int left_size = root_idx;                    // 左子树节点个数int right_size = in_len - root_idx - 1;      // 右子树节点个数// 步骤4：递归构建左子树// 左子树的后序：从post_order[0]开始，取left_size个元素// 左子树的中序：从in_order[0]开始，取left_size个元素root->left = buildTreeFromPostIn(post_order, left_size, in_order, left_size);// 步骤5：递归构建右子树// 右子树的后序：从post_order[left_size]开始，取right_size个元素// 右子树的中序：从in_order[root_idx+1]开始，取right_size个元素root->right = buildTreeFromPostIn(post_order + left_size, right_size, in_order + root_idx + 1, right_size);return root;
}// 前序遍历（用于验证结果）
void preorder(TreeNode* root) {if (root == NULL) {return;}printf("%s ", root->val);preorder(root->left);preorder(root->right);
}// 释放二叉树内存
void freeTree(TreeNode* root) {if (root == NULL) {return;}freeTree(root->left);freeTree(root->right);free(root);
}

读取序列数组：

int main() {int n;scanf("%d", &n);getchar();  // 读取换行符// 动态分配内存char** post_order = (char**)malloc(n * sizeof(char*));char** in_order = (char**)malloc(n * sizeof(char*));for (int i = 0; i < n; i++) {post_order[i] = (char*)malloc(10 * sizeof(char));in_order[i] = (char*)malloc(10 * sizeof(char));}// 使用gets读取后序遍历序列char post_line[1000];gets(post_line);char* token = strtok(post_line, " ");int i = 0;while (token != NULL && i < n) {strcpy(post_order[i++], token);token = strtok(NULL, " ");}// 使用gets读取中序遍历序列char in_line[1000];gets(in_line);token = strtok(in_line, " ");i = 0;while (token != NULL && i < n) {strcpy(in_order[i++], token);token = strtok(NULL, " ");}// 重建二叉树TreeNode* root = buildTree(post_order, n, in_order, n);// 输出前序遍历结果preorder(root);// 释放内存for (int i = 0; i < n; i++) {free(post_order[i]);free(in_order[i]);}free(post_order);free(in_order);freeTree(root);return 0;
}

题目三：有空值

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef struct TreeNode {char val[10];struct TreeNode* left;struct TreeNode* right;
} TreeNode;// 检查是否为空节点
int isNullNode(char* str) {return str == NULL || strcmp(str, "NULL") == 0 || strcmp(str, "null") == 0 || strcmp(str, "0") == 0 ||strlen(str) == 0;
}// 在中序数组中找到目标值的位置（跳过空节点）
int findIndex(char** in_order, int len, char* target) {for (int i = 0; i < len; i++) {// 跳过空节点if (isNullNode(in_order[i])) {continue;}if (strcmp(in_order[i], target) == 0) {return i;}}return -1;
}// 计算实际节点数（跳过空节点）
int countActualNodes(char** array, int len) {int count = 0;for (int i = 0; i < len; i++) {if (!isNullNode(array[i])) {count++;}}return count;
}// 根据后序和中序重建二叉树（支持空节点）
TreeNode* buildTreeFromPostIn(char** post_order, int post_len, char** in_order, int in_len) {// 基准情况：如果数组为空，返回NULLif (post_len <= 0 || in_len <= 0) {return NULL;}// 步骤1：找到后序中最后一个非空节点作为根节点char* root_val = NULL;int root_post_index = -1;// 从后往前找第一个非空节点for (int i = post_len - 1; i >= 0; i--) {if (!isNullNode(post_order[i])) {root_val = post_order[i];root_post_index = i;break;}}// 如果没找到非空节点，说明都是空节点if (root_val == NULL) {return NULL;}TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));strcpy(root->val, root_val);root->left = NULL;root->right = NULL;// 步骤2：在中序数组中找到根节点的位置int root_idx = findIndex(in_order, in_len, root_val);if (root_idx == -1) {printf("错误：在中序序列中找不到根节点 %s\n", root_val);free(root);return NULL;}// 步骤3：计算左右子树的边界（关键修改）// 计算左子树的实际节点数（在中序中根节点左边的非空节点数）int left_actual_count = 0;for (int i = 0; i < root_idx; i++) {if (!isNullNode(in_order[i])) {left_actual_count++;}}// 计算右子树的实际节点数（在中序中根节点右边的非空节点数）int right_actual_count = 0;for (int i = root_idx + 1; i < in_len; i++) {if (!isNullNode(in_order[i])) {right_actual_count++;}}// 步骤4：构建左子树的后序序列// 左子树的后序序列是后序数组的前left_actual_count个非空节点char** left_post = NULL;if (left_actual_count > 0) {left_post = (char**)malloc(left_actual_count * sizeof(char*));int count = 0;for (int i = 0; i < root_post_index && count < left_actual_count; i++) {if (!isNullNode(post_order[i])) {left_post[count++] = post_order[i];}}}// 步骤5：构建右子树的后序序列// 右子树的后序序列是后序数组中剩下的right_actual_count个非空节点char** right_post = NULL;if (right_actual_count > 0) {right_post = (char**)malloc(right_actual_count * sizeof(char*));int count = 0;int found = 0;for (int i = 0; i < root_post_index && count < right_actual_count; i++) {if (!isNullNode(post_order[i])) {if (found >= left_actual_count) {right_post[count++] = post_order[i];}found++;}}}// 步骤6：递归构建左右子树root->left = buildTreeFromPostIn(left_post, left_actual_count, in_order, root_idx);root->right = buildTreeFromPostIn(right_post, right_actual_count, in_order + root_idx + 1, in_len - root_idx - 1);// 释放临时数组if (left_post != NULL) free(left_post);if (right_post != NULL) free(right_post);return root;
}// 前序遍历（显示空节点）
void preorderWithNull(TreeNode* root) {if (root == NULL) {printf("NULL ");return;}printf("%s ", root->val);preorderWithNull(root->left);preorderWithNull(root->right);
}// 中序遍历（显示空节点）
void inorderWithNull(TreeNode* root) {if (root == NULL) {printf("NULL ");return;}inorderWithNull(root->left);printf("%s ", root->val);inorderWithNull(root->right);
}// 释放二叉树内存
void freeTree(TreeNode* root) {if (root == NULL) {return;}freeTree(root->left);freeTree(root->right);free(root);
}