关键词解释:梯度下降法(Gradient Descent)
梯度下降法(Gradient Descent)是优化中最基础且核心的算法之一。无论是一维还是多维问题,其核心思想一致:沿着目标函数梯度的反方向更新参数,以逐步逼近极小值点。下面我们从一维和多维两个角度详细解析,并辅以数学公式与代码示例。
一、基本思想回顾
给定目标函数 ,其中
是参数向量,梯度下降的更新规则为:
:学习率(步长)
:函数在
处的梯度(一阶导数向量)
关键区别:
- 一维:梯度退化为普通导数(标量)
- 多维:梯度是偏导数组成的向量
二、一维梯度下降(标量参数)
1. 场景
优化一个单变量函数,例如:
2. 数学形式
- 梯度:
- 更新规则:
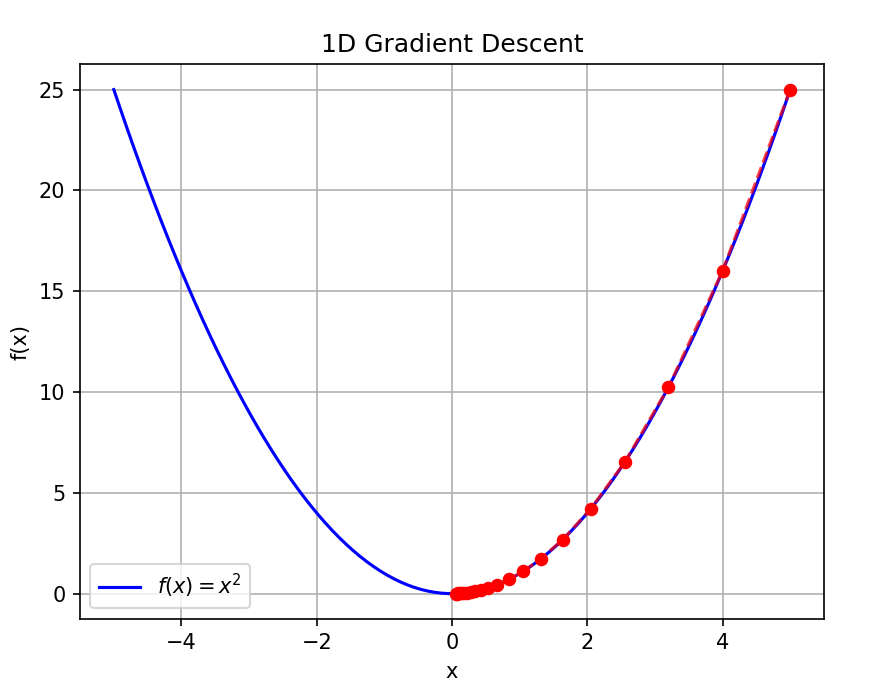
3. 示例:最小化
- 导数:
- 更新:
收敛条件:
4. Python 代码演示(一维)
import numpy as np
import matplotlib.pyplot as pltdef f(x):return x ** 2def df_dx(x):return 2 * x# 参数
x = 5.0 # 初始点
lr = 0.1 # 学习率
steps = 20history = [x]
for _ in range(steps):grad = df_dx(x)x = x - lr * gradhistory.append(x)# 可视化
x_vals = np.linspace(-5, 5, 100)
plt.plot(x_vals, f(x_vals), 'b-', label='$f(x)=x^2$')
plt.scatter(history, [f(x) for x in history], c='red', s=30, zorder=5)
plt.plot(history, [f(x) for x in history], 'r--', alpha=0.7)
plt.title('1D Gradient Descent')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()
三、多维梯度下降(向量参数)
1. 场景
优化多变量函数,例如:
- 线性回归:
- 神经网络损失函数
2. 数学形式
设参数为向量
梯度:
更新规则(逐元素):
3. 示例:最小化 
- 梯度:
- 更新:
最小值在。
4. Python 代码演示(二维)
import numpy as np
import matplotlib.pyplot as pltdef f(x, y):return x**2 + y**2def grad_f(x, y):return np.array([2*x, 2*y])# 初始化
theta = np.array([3.0, 2.0]) # [x, y]
lr = 0.1
steps = 20history = [theta.copy()]
for _ in range(steps):grad = grad_f(theta[0], theta[1])theta = theta - lr * gradhistory.append(theta.copy())history = np.array(history)# 绘制等高线 + 路径
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)plt.contour(X, Y, Z, levels=20, cmap='viridis')
plt.plot(history[:, 0], history[:, 1], 'ro-', label='GD Path')
plt.scatter(0, 0, c='red', marker='*', s=200, label='Minimum')
plt.title('2D Gradient Descent on $f(x,y)=x^2+y^2$')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.show()
四、一维 vs 多维对比总结
| 特性 | 一维梯度下降 | 多维梯度下降 |
|---|---|---|
| 参数 | 标量 | 向量 |
| 梯度 | 导数 | 梯度向量 $\nabla f$($n$ 维) |
| 更新 | ||
| 几何意义 | 在曲线上左右移动 | 在曲面/超曲面上沿最陡下降方向移动 |
| 应用 | 教学示例、简单优化 | 机器学习、深度学习、工程优化 |
五、注意事项(多维特有)
特征尺度差异
若各维度量纲不同(如是身高(cm),
是收入(万元)),会导致梯度方向扭曲 → 需标准化(Standardization)
病态条件(Ill-conditioning)
Hessian 矩阵条件数大 → 梯度下降呈“锯齿状”震荡 → 可用 动量(Momentum) 或 二阶方法(如牛顿法)局部极小值与鞍点
多维非凸函数可能存在多个极小值或鞍点(梯度为零但非极值)→ Adam 等优化器更鲁棒
六、扩展:批量梯度下降(机器学习中的多维应用)
在线性回归中,损失函数为:
梯度为:
更新:
这就是多维梯度下降在机器学习中的典型应用。
总结
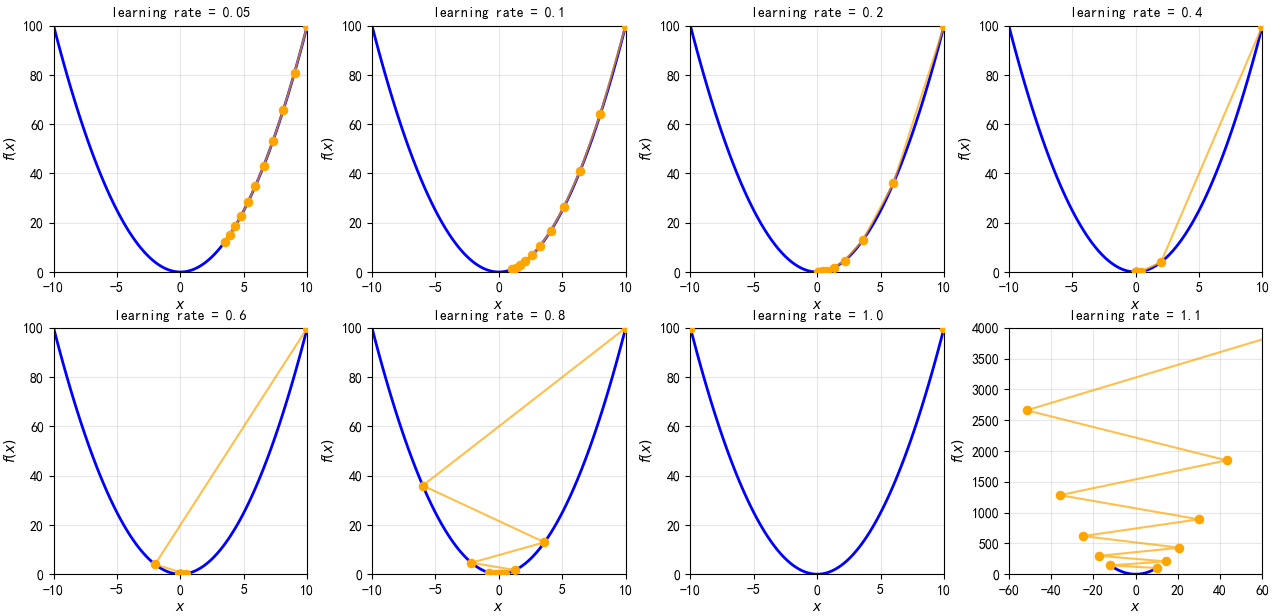
- 一维:理解原理的“玩具模型”,直观展示学习率影响
- 多维:真实世界的优化问题,需处理向量、矩阵、尺度、收敛性等复杂性
- 核心不变:始终沿负梯度方向更新参数
💡 记住:无论维度多少,梯度下降的本质都是——“往最陡的下坡方向走一步”。
