背包DP合集

01背包

介绍：

01背包是处理当前有限的物品中，选择固定的体积可以获得出的价值最大的问题

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){int m,n;while(cin>>m>>n){if(m==0&&n==0)break;vector<pair<int,int>>a(n+1);for(int i=1;i<=n;i++)cin>>a[i].first>>a[i].second;vector dp(n+1,vector<int>(m+1));//表示到第i个位置为止，占用了j的体积的总价值最大是多少for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j>=a[i].first)dp[i][j]=max(dp[i-1][j],dp[i-1][j-a[i].first]+a[i].second);else dp[i][j]=dp[i-1][j];}}cout<<dp[n][m]<<'\n';}
}

空间优化：

滚动数组优化：

可以发现它的转移与前面的一行的状态有关，所以可以只维护两行数组即可

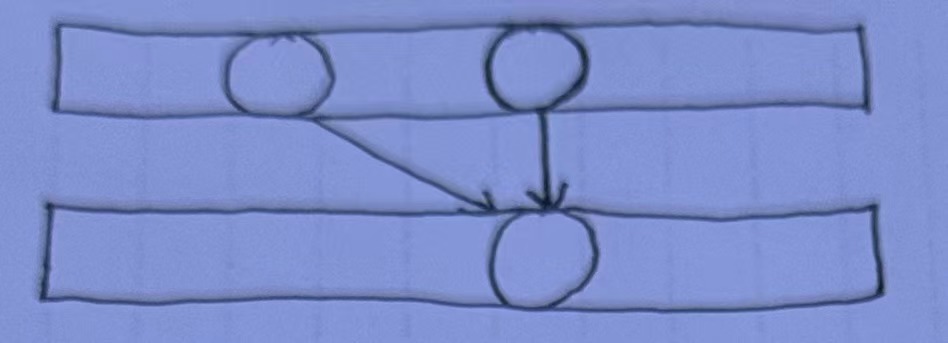
代码：

#include<bits/stdc++.h>
using namespace std;
int main(){int m,n;while(cin>>m>>n){if(m==0&&n==0)break;vector<pair<int,int>>a(n+1);for(int i=1;i<=n;i++)cin>>a[i].first>>a[i].second;vector dp(2,vector<int>(m+1));for(int i=1;i<=n;i++){int y=i&1;for(int j=1;j<=m;j++){if(j>=a[i].first)dp[y][j]=max(dp[y^1][j],dp[y^1][j-a[i].first]+a[i].second);else dp[y][j]=dp[y^1][j];}}cout<<dp[n&1][m]<<'\n';}
}

优化为一维：

可以发现当前转移是根据前面的转移的，想想是否可以将其压缩为一维，因为每一个数都是根据前面的数转移的，所以需要维护前面的数不被改变，可以从后往前开始遍历

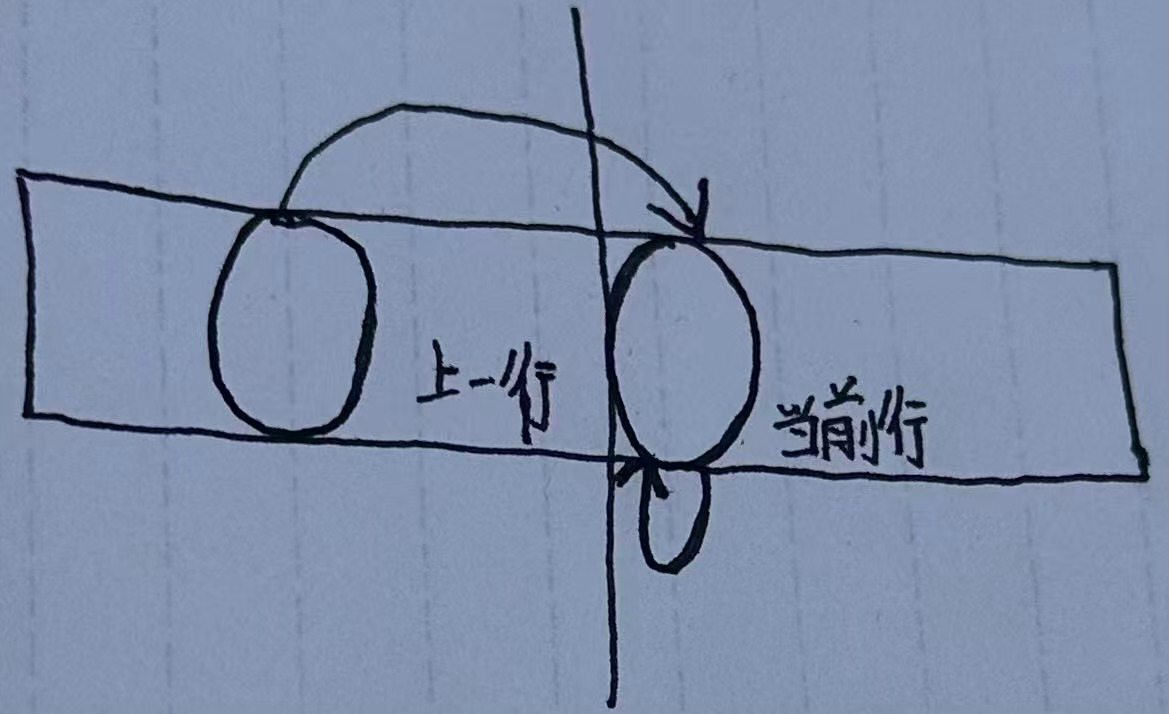
代码：

#include<bits/stdc++.h>
using namespace std;
int main(){int m,n;while(cin>>m>>n){if(m==0&&n==0)break;vector<pair<int,int>>a(n+1);for(int i=1;i<=n;i++)cin>>a[i].first>>a[i].second;vector<int>dp(m+1);for(int i=1;i<=n;i++){for(int j=m;j>=a[i].first;j--){dp[j]=max(dp[j],dp[j-a[i].first]+a[i].second);}}cout<<dp[m]<<'\n';}
}

完全背包

介绍：

不同于01背包的区别是每一个数可以无限次选取

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){int m,n;cin>>m>>n;vector<pair<int,int>>a(n+1);for(int i=1;i<=n;i++)cin>>a[i].second>>a[i].first;vector dp(n+1,vector<int>(m+1));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j>=a[i].first)dp[i][j]=max(dp[i-1][j],dp[i][j-a[i].first]+a[i].second);else dp[i][j]=dp[i-1][j];}}cout<<dp[n][m]<<'\n';
}

空间优化

滚动数组优化：

和上述一样，只不过状态转移不一样

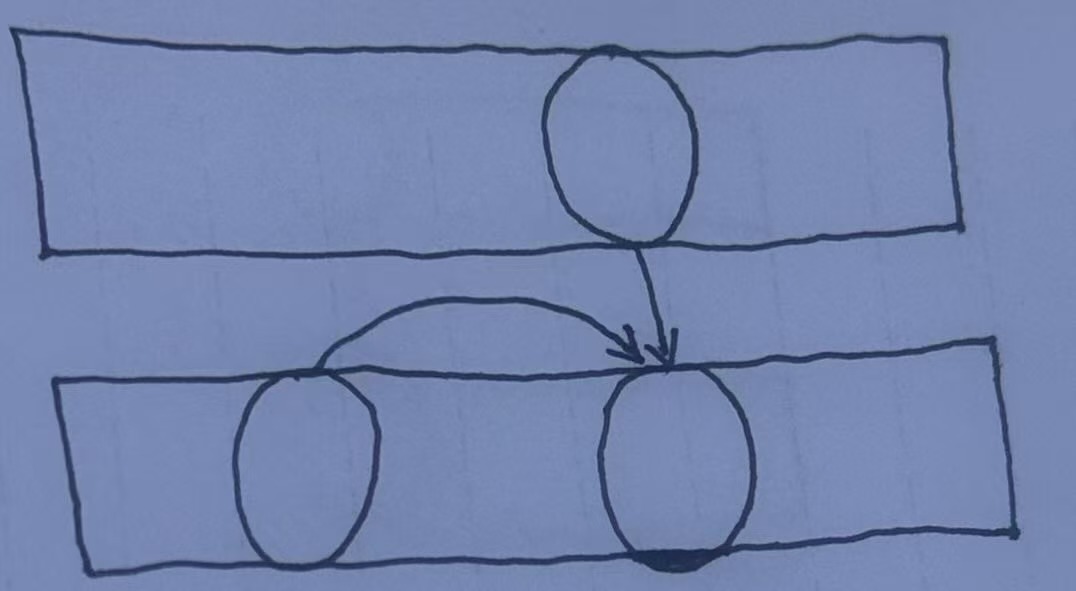
代码：

#include<bits/stdc++.h>
using namespace std;
int main(){int m,n;cin>>m>>n;vector<pair<int,int>>a(n+1);for(int i=1;i<=n;i++)cin>>a[i].second>>a[i].first;vector dp(2,vector<int>(m+1));for(int i=1;i<=n;i++){int y=i&1;for(int j=1;j<=m;j++){if(j>=a[i].first)dp[y][j]=max(dp[y^1][j],dp[y][j-a[i].first]+a[i].second);else dp[y][j]=dp[y^1][j];}}cout<<dp[n&1][m]<<'\n';
}

优化为一维

和上述的情况唯一的区别就是可以选择无数次，也就是可以从之前的状态转移过来

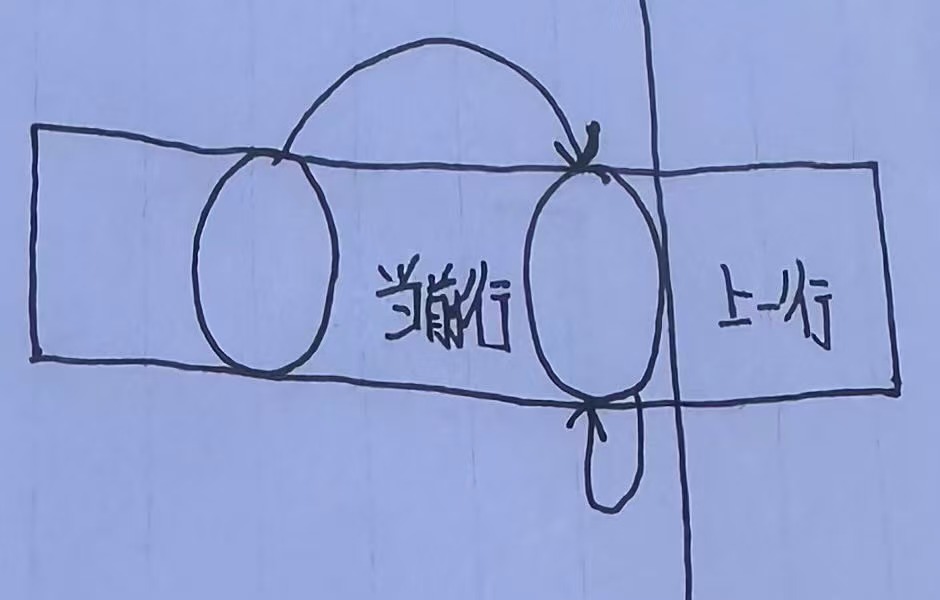
代码：

#include<bits/stdc++.h>
using namespace std;
int main(){int m,n;cin>>m>>n;vector<pair<int,int>>a(n+1);for(int i=1;i<=n;i++)cin>>a[i].second>>a[i].first;vector<int>dp(m+1);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j>=a[i].first)dp[j]=max(dp[j],dp[j-a[i].first]+a[i].second);else dp[j]=dp[j];}}cout<<dp[m]<<'\n';
}

多重背包

介绍：

现在给定n种物品，每种物品有s个，求解容量为m的包中可以取到的最大价值

代码：

//将n件物品拆开即可
#include<bits/stdc++.h>
using namespace std;
int main(){int m,n;cin>>m>>n;vector<pair<int,int>>a;a.push_back({0,0});for(int i=1;i<=n;i++){int s,w,v;cin>>s>>w>>v;while(s--){a.push_back({v,w});}}int k=a.size()-1;vector<int>dp(m+1);for(int i=1;i<=k;i++){for(int j=m;j>=a[i].first;j--){dp[j]=max(dp[j],dp[j-a[i].first]+a[i].second);}}cout<<dp[m]<<'\n';
}

二进制优化多重背包

代码：

//可以发现，二进制数可以表示出每一个数，所有可以将多重背包存储为分别有多少个二进制数来表示当前的数
#include<bits/stdc++.h>
using namespace std;
struct node{int v,w,cnt;
};
int main(){int m,n;cin>>m>>n;vector<node>a;a.push_back({0,0});for(int i=1;i<=n;i++){int s,w,v;cin>>s>>w>>v;int k=1;while(s>=k){s-=k;a.push_back({v,w,k});k*=2;}if(s){a.push_back({v,w,s});}}vector<int>dp(m+1);int k=a.size()-1;for(int i=1;i<=k;i++){for(int j=m;j>=a[i].cnt*a[i].v;j--){dp[j]=max(dp[j],dp[j-a[i].cnt*a[i].v]+a[i].w*a[i].cnt);}}cout<<dp[m]<<'\n';
}