数据结构之栈和队列-队列

目录

前言

一、队列的概念

二、队列的结构

三、队列的相关方法实现

  1、队列的初始化

  2、队列的销毁

  3、队列的插入数据(入队列：队尾)

  4、队列的删除数据(出队列：队头)

  5、取队头数据

  6、取队尾数据

  7、队列判空

  8、队列有效元素个数

   测试打印队列

四、队列的相关算法题

  1、用队列实现栈

  2、用栈实现队列

  3、设计循环队列

结束语

---

前言

      在上一篇文章数据结构之栈和队列-栈中我们详细讲解了栈这个数据结构，栈最特殊的地方就在于其数据遵守后进先出的原则。而本篇文章我就为大家讲解另一个数据结构：队列。

一、队列的概念

      概念：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列中的数据元素遵守先进先出FIFO(FirstIn First Out)的原则。
      入队列：进行插入操作的一端称为队尾
      出队列：进行删除操作的一端称为队头

      用图就可以让大家更好去理解队列的概念：

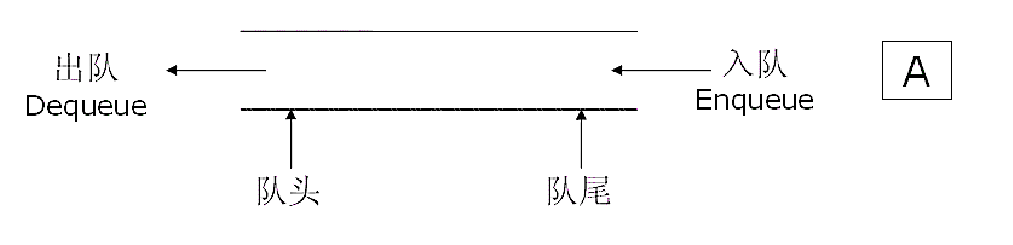
      大家可以把队列理解成火车过隧道这种，一定是火车头先进隧道然后火车头先出隧道，就可以类比为队列数据先进先出的原则，这样就可以更好理解队列了。
      而队列在公平性这样的问题中是运用很多的，比如医院或者饭馆抽号，抽号的原则就是先来的人一定是先被服务的，并且可以查看前面还要多少人，这就是利用队列实现的。

二、队列的结构

      队列底层结构选型：队列也可以数组和链表的结构实现，但使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，在前面学习顺序表我们也知道顺序表的头删就比较麻烦，删完数据后还需要循环将其余数据往前移一位，效率会比较低。

//Queue.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int QDataType;typedef struct QNode //队列的节点结构
{QDataType val;struct QNode* next;
}QNode;typedef struct Queue //队列结构
{struct QNode* phead; //队头struct QNode* ptail; //队尾int size; //队列的节点个数
}Queue;

      我们会发现队列虽然是靠链表的结构进行实现，但我们不仅定义了队列节点的结构，还定义了队列结构，在前面我们学习单链表时却只是定义了链表节点的结构。
      原因是在于避免多次使用二级指针而造成麻烦，因为我们知道链表要让实参进行改变就需要进行地址传参也就是要使用二级指针。
      由于队列遵守先进先出的原则，也就是对应链表的尾插和头删，而如果只有这两个操作的话我们就可以再创建一个队尾节点(ptail)，也是为了后续的插入删除和获取数据更方便。但此时由于我们创建了头节点(phead)和尾节点(ptail)两个节点，如果不将其“包装”在结构体内，则函数的形参就需要两个二级指针进行地址传参，这样就会使我们的代码更加复杂化。

      但讲了这么多为什么把头尾节点“包装”在一个新结构体内就可以使用一级指针呢？
      在这就可以类似于前面学习的顺序表了，顺序表之所以只需要一级指针就可以实现，原因就在于我们在更改顺序表的数据时自始至终都没有对顺序表结构体本身的地址进行修改，而只是对其内部的成员进行修改。这句话是非常重要的，这也就解释了为什么单链表需要二级指针，因为单链表的头插节点数据是需要对头节点本身的地址进行修改，让头节点指向新的节点地址，这就必须使用二级指针才能修改实参。
      而如果在队列中我们将头尾节点“包装”成新的结构体，当我们需要修改头节点地址时对于这个结构体而言也只是修改其内部的成员，而不会改变结构体本身的地址，所以对新结构体而言就可以使用一级指针进行传参。

三、队列的相关方法实现

  1、队列的初始化

//Queue.h
//初始化队列
void QueueInit(Queue* pq);//Queue.c
#include "Queue.h"//初始化队列
void QueueInit(Queue* pq)
{pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}

  2、队列的销毁

//Queue.h
//销毁队列
void QueueDestroy(Queue* pq);//Queue.c
//销毁队列
void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->phead;while (cur)//释放队列的所有节点{QNode* next = cur->next;free(cur);cur = next;}pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}

  3、队列的插入数据(入队列：队尾)

//Queue.h
//创建节点
QNode* CreateNode(QDataType x);
//队列插入数据(入队列：队尾)
void QueuePush(Queue* pq, QDataType x);//Queue.c
//创建节点
QNode* CreateNode(QDataType x)
{QNode* newnode = (QNode*)malloc(sizeof(QNode));assert(newnode); //判断节点是否创建成功newnode->next = NULL;newnode->val = x;return newnode;
}//队列插入数据(入队列：队尾)
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = CreateNode(x);if (pq->phead == NULL)//队列没有节点则直接插入{pq->phead = pq->ptail = newnode;}else//队列有节点则进行尾插{pq->ptail->next = newnode; //原尾节点与新节点相连pq->ptail = newnode; //改变尾节点位置}pq->size++; //队列节点数加一
}

  4、队列的删除数据(出队列：队头)

//Queue.h
//队列删除数据(出队列：队头)
void QueuePop(Queue* pq);//Queue.c
//队列删除数据(出队列：队头)
void QueuePop(Queue* pq)
{assert(pq);assert(pq->size); //队列无数据时不能删除QNode* next = pq->phead->next;if (pq->phead == pq->ptail)//如果队列只有一个节点，此时phead和ptail在同一个位置//释放phead空间也就把ptail空间释放了，所以ptail也要置为空指针，不然就是野指针了{free(pq->phead);pq->ptail = pq->phead = NULL;}else{free(pq->phead);pq->phead = next;}pq->size--; //队列节点数减一
}

  5、取队头数据

//Queue.h
//取队头数据
QDataType QueueFront(Queue* pq);//Queue.c
//取队头数据
QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->size); //获取数据前提也是队列要用数据return pq->phead->val;
}

  6、取队尾数据

//Queue.h
//取队尾数据
QDataType QueueBack(Queue* pq);//Queue.c
//取队尾数据
QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->size); //获取数据前提也是队列要用数据return pq->ptail->val;
}

  7、队列判空

//Queue.h
//队列判空
bool QueueEmpty(Queue* pq);//Queue.c
//队列判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}

  8、队列有效元素个数

//Queue.h
//队列有效元素个数
int QueueSize(Queue* pq);//Queue.c
//队列有效元素个数
int QueueSize(Queue* pq)
{assert(pq);return pq->size; //队列结构体的size成员在这里就起到作用了//不需要再去遍历一边队列，直接返回pq->size值即可
}

   测试打印队列

//Test.c
#include "Queue.h"void Test1()
{Queue q1;QueueInit(&q1); //队列初始化QueuePush(&q1, 1); //队列插入数据QueuePush(&q1, 2);QueuePush(&q1, 3);QueuePush(&q1, 4);while (QueueSize(&q1)){printf("%d ", QueueFront(&q1)); //获取队头数据QueuePop(&q1); //每获取到队头数据则进行出队列}QueueDestroy(&q1); //销毁队列
}int main()
{Test1();return 0;
}

四、队列的相关算法题

  1、用队列实现栈

      这道算法题并没有什么实际意义主要是为了帮助大家巩固栈和队列的知识以及两者之间的差别，我们知道队列是遵守先进先出的原则，而栈是遵守先进后出的原则，所以我们就可以利用两个队列来实现栈先进后出的功能。

      由于队列只能先进先出，那两个队列怎么实现一个栈的功能呢？我们想一下如果现在有一个队列q1里面有数据另一个队列q2没有数据，我们是不是就要把q1的最后一个数据进行返回才是后进先出的情况。那怎么做到呢？
      这其实就需要借助q2了，由于q2此时没有数据，我们可以先将q1前面的所有数据循环出队列放入到q2中，只剩下我们需要返回的最后一个数据，此时q1只有一个数据再出队列我们就不再放入q2而是直接返回这个值即可实现栈后进先出的功能。
      这个地方需要注意的点在于我们必须要时刻保证其中一个队列中一定没有数据，才能让这个队列对有数据的队列进行导入，否则后续代码会非常容易判断失误。

      而由于这个算法题在C语言中没有包含队列的功能，所以需要我们先把前面队列相关方法实现的代码全部写一遍才行，在这里就不重新写一遍了，直接实现栈的功能，所调用的函数如有不清楚的可以回看上面的队列相关方法实现：

typedef struct 
{Queue q1;Queue q2; //两个队列实现栈功能
} MyStack;MyStack* myStackCreate() 
{MyStack* pst = (MyStack*)malloc(sizeof(MyStack));QueueInit(&(pst->q1)); //时刻注意栈的成员是队列结构体，调用函数不能忘记取地址&QueueInit(&(pst->q2)); //->优先级高于&，可以不打括号return pst;
}void myStackPush(MyStack* obj, int x) 
{//有数据的队列进行入栈，无数据的队列才对有数据的队列进行导入if(QueueSize(&(obj->q1)) != 0){QueuePush(&(obj->q1), x);}else{QueuePush(&(obj->q2), x);}
}int myStackPop(MyStack* obj) 
{//在移除并返回栈顶元素之前则需要借助无数据的队列将前面size - 1个数据先进行导入//再把栈顶数据移除并返回//有数据的队列进行入栈，无数据的队列才对有数据的队列进行导入//用假设法判断哪个队列为空，则后续只需要写一遍入栈代码，否则需要if条件写两遍Queue* empty = &(obj->q1); //假设队列q1为空Queue* nonempty = &(obj->q2);if(QueueSize(&(obj->q1)) != 0)//假设不对，则队列q1不为空{empty = &(obj->q2);nonempty = &(obj->q1);}//此时队列empty就是进行导入，队列nonempty进行入栈，不需要再判断q1、q2谁是空了while(QueueSize(nonempty) > 1)//为了保留栈顶元素{QueuePush(empty, QueueFront(nonempty));//意思是将有数据的队列取队头数据QueueFront的值，入队列QueuePush到无数据的队列QueuePop(nonempty); //入队列一个数据则将其出队列}int top = QueueFront(nonempty); //取出栈顶数据QueuePop(nonempty); //移除栈顶数据return top; //返回栈顶数据
}int myStackTop(MyStack* obj) 
{if(QueueSize(&obj->q1) != 0){return QueueBack(&(obj->q1));}else{return QueueBack(&(obj->q2));}
}bool myStackEmpty(MyStack* obj) 
{//栈为空的条件是两个成员即两个队列都为空才满足return QueueEmpty(&(obj->q1)) && QueueEmpty(&(obj->q2));
}void myStackFree(MyStack* obj) 
{//栈的释放和上面一样，需要两个成员即两个队列都进行了释放，最后释放栈才满足QueueDestroy(&(obj->q1));QueueDestroy(&(obj->q2));free(obj);obj = NULL;
}

  2、用栈实现队列

      我们能用两个队列实现栈的功能，自然也就可以用两个栈来实现队列的功能，也就是说利用栈后进先出的原则来实现队列先进先出的原则。

      虽然两者的代码逻辑是相似的，但还是有一些不同点需要注意：
      首先就是两个栈怎么定义，难道还是像上面一样判断谁空睡不空吗？我们想一下，如果此时有一个栈存放1、2、3、4这些数据，我要实现队列的功能取出数据，那也就是需要取出1这个数据，只靠一个栈肯定实现不了，所以这就要用到另一个空栈来存放数据。由于栈是后进先出，所以空栈里面存放的数据顺序就是4、3、2、1，然后我们再进行出栈，则此时获取到的数据就是1了。
      这样看来好像就没什么问题了，但是我们仔细想想，如果是以空和不空来判断两个栈，我们怎么知道那个不空的栈数据的顺序是我们想要的？
      所以这两个栈的定义方式就和上面的题有所不同了，我们需要定义一个栈stpush是专门来存放插入进来的数据，而另一个栈stpop是专门进行出栈并返回数据的，这样我们就只需要将stpush的数据按要求存放到stpop即可一直保证数据的顺序不会出现问题。

      而这道题依然在C语言中没有包含栈的功能，所以需要我们先把前面栈相关方法实现的代码全部写一遍才行，在这里就不重新写一遍了，直接实现队列的功能，所调用的函数如有不清楚的可以回看之前的文章数据结构之栈和队列-栈，具体代码如下(里面也有详细的批注供大家理解)：

typedef struct 
{ST stpush;//专门用来存放新加的数据ST stpop; //专门用来返回并移除数据，所返回数据即为队头数据
} MyQueue;MyQueue* myQueueCreate() 
{MyQueue* queue = (MyQueue*)malloc(sizeof(MyQueue));STInit(&(queue->stpush));STInit(&(queue->stpop));return queue;
}void myQueuePush(MyQueue* obj, int x) 
{STPush(&(obj->stpush), x); //每次执行push指令时新加的数据直接放入栈stpush即可
}int myQueuePop(MyQueue* obj) 
{if(STSize(&(obj->stpop)) == 0)//说明队列stpop无数据，需要将stpush的数据全部放过来,再取出栈顶数据{while(STSize(&(obj->stpush))){STPush(&(obj->stpop), STTop(&(obj->stpush)));//相当于把栈stpush的栈顶数据取出来放入stpop的栈底，此时数据的顺序就反转了STPop(&(obj->stpush));//每次取出数据就进行出栈}}//如果此时队列stpop仍然有数据，则if语句不会执行，直接返回stpop的栈顶数据即可，//也就满足了队列后进的数据不会影响队头数据的取出int front = STTop(&(obj->stpop));STPop(&(obj->stpop));return front;
}int myQueuePeek(MyQueue* obj) 
{if(STSize(&(obj->stpop)) == 0){while(STSize(&(obj->stpush))){STPush(&(obj->stpop), STTop(&(obj->stpush)));STPop(&(obj->stpush));}}return STTop(&(obj->stpop)); //myQueuePeek和myQueuePop唯一不同点就是不需要出栈数据，返回即可
}bool myQueueEmpty(MyQueue* obj) 
{return STEmpty(&(obj->stpush)) && STEmpty(&(obj->stpop));
}void myQueueFree(MyQueue* obj) 
{STDestroy(&(obj->stpush));STDestroy(&(obj->stpop));free(obj);obj = NULL;
}

  3、设计循环队列

      循环队列在题目中已经提到了就是一种队尾被连接在队首之后以形成一个循环的队列，并且也遵守数据先进先出的原则。那有些人就想需要队尾与队首进行相连用循环链表不就可以实现吗？的确如此，但其实循环链表实现整道题的难度是比用数组实现更大的。
      那有些人就会想数组怎么能让队尾与队头相连呢？正常方法肯定不行的

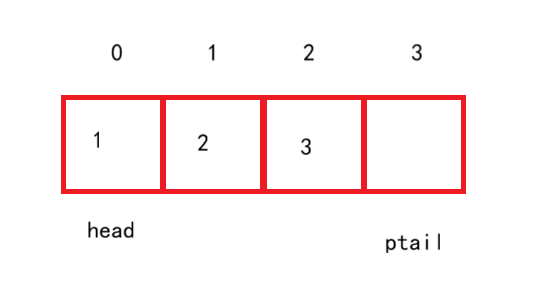
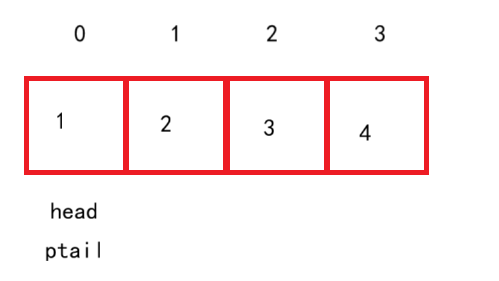
      如图所示，首先初始化一个空数组让head和ptail处于同一个位置，当ptail到末尾时，此时数组还有一个空位置可以插入数据，此时如果再插入数据的话按照循环队列的逻辑来说ptail应该就要回到开头与head重合，但数组本身没有这个功能，当再插入一个数据则ptail加1跳到下标为4的位置，这样就和导致越界访问了。
      所以我们需要想一个办法能让末尾的ptail回到开头，这里我们就用到了模运算：我们知道模运算是取余数，所以当我们假设k为数组的总大小为4，则 ptail = ptail % (k - 1) 这个代码就能实现数组的末尾回到开头。当ptail不在尾时即小于3，则 ptail % 3 的值还是ptail本身；而当ptail在尾时也就是下标为3时，则ptail = ptail % 3 = 0；则ptail就i回到了开头，实现了循环功能。

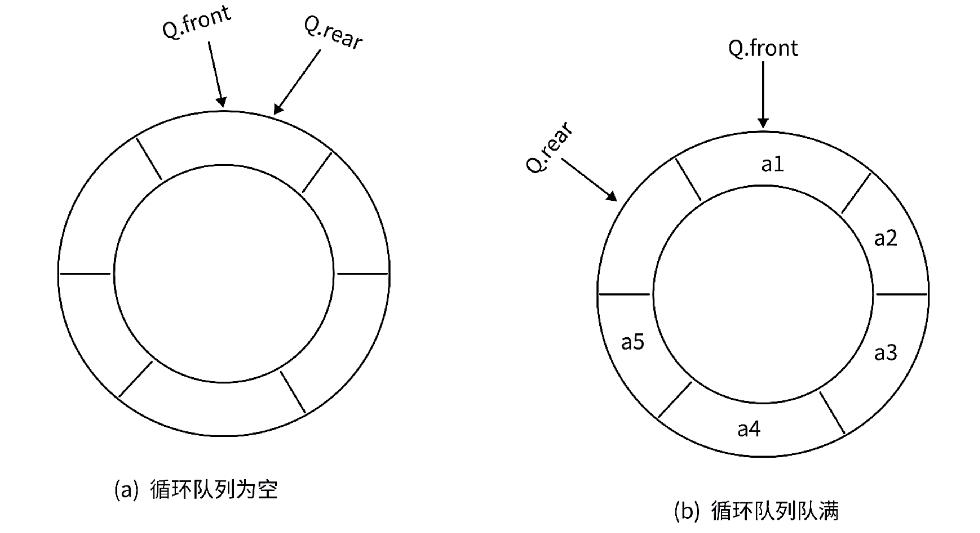
      上面的图就是利用数组实现循环队列的样子，在这里我们会发现左边的图中循环队列为空时队头front和队尾rear在同一个位置好理解，但是右边的图中队列中还有一个空位置没有放入数据，却显示循环队列已满，为什么要这样呢？

      左边的图我们就会发现当队头队尾处于同一个位置时我们就能判断此时循环队列为空，那两者处于同一个位置就一定能确定此时队列就是没有数据吗？我们不妨再以上面数组的图为例：当此时数组还有一个空位置我们再插入数据时，由循环队列的特性我们会发现

      此时队头和队尾也重合在一起了，那这样我们就发现了问题：当两者重合时可能是循环队列没有数据，也可能是此时队列数据已满，那我们就不能通过两者处于同一位置来判断队列为空了，这其实也叫做假溢出问题。
      而解决办法就是上面右边的图了，我们对一个能存放数据的有效空间k的数组在多开辟一个空间，而这个空间我们不能存放数据，当队列中只剩下一个没有数据的空间时我们就判断此时队列数据已满。这样的好处就在于能保证当head == ptail时只有队列为空这一种情况，而由右图我们就知道当ptail + 1 == head时则说明此时队列数据已满。

具体代码如下，每个函数我都进行了相关批注来详细讲解代码的思路：

typedef struct 
{int* arr; //数组实现循环队列int head; //队头int tail;//队尾(注意由于初始head和ptail在同一个位置，插入一个数据ptail跳一格，ptail实际为尾数据的下一个位置)int k;    //循环队列的有效空间总个数
} MyCircularQueue;MyCircularQueue* myCircularQueueCreate(int k) 
{MyCircularQueue* cq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));//创建循环队列cq->arr = (int*)malloc(sizeof(int) * (k + 1));//多开辟一个空间解决假溢出问题cq->head = 0;cq->tail = 0;cq->k = k; //队列能存放数据的有效空间为kreturn cq;
}bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{return obj->head == obj->tail; //队头队尾重合即队列为空
}bool myCircularQueueIsFull(MyCircularQueue* obj) 
{return (obj->tail + 1) % (obj->k + 1) == obj->head;//模运算的作用已经说明了，就是为了满足tail在数组尾部时能回到开头//判满条件就是：tail + 1 == head，但如果tail已经在数组尾部，如果只是加1则就会越界访问，就需要模运算
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value)
{if(myCircularQueueIsFull(obj)){return false; //如果队列已满则不能再添加数据，返回false}else{obj->arr[obj->tail] = value;obj->tail++;//只让tail加还是可能导致越界访问的问题，所以只要是让head或者tail移动的地方都需要进行模运算obj->tail %= (obj->k + 1);return true;}
}bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{if(myCircularQueueIsEmpty(obj)){return false; //如果队列为空则不能删除数据，返回false}else{obj->head++;obj->head %= (obj->k + 1);//删除数据的代码要着重讲解一下：由于我们的队列是利用数组实现的，而我们的数组是malloc函数进行开辟//整个数组是作为一个整体的，这样我们是不能对数组的其中一个元素进行删除//所以我们只需要让队头跳一格就行了//这里可能就有人问了：那数据不还在那里存放吗，这样不会对判断队列是否为空造成影响吗？//其实循环队列是否已满或为空根本不是靠数组里面是否有数据来判断//完完全全就是靠队头和队尾进行判断，只要队头与队尾重合则循环队列为空；队尾的下一个位置为队头则队列已满//而原因在这个题目开头已经解释了return true;}
}int myCircularQueueFront(MyCircularQueue* obj) 
{if(myCircularQueueIsEmpty(obj)){return -1; //如果队列为空则不能获取队头数据，返回-1}else{return obj->arr[obj->head];}
}int myCircularQueueRear(MyCircularQueue* obj) 
{if(myCircularQueueIsEmpty(obj)){return -1; //如果队列为空则不能获取队尾数据，返回-1}else{//return obj->arr[obj->tail - 1];//err：错误原因还是因为没有实现数组循环的功能//如果此时ptrail处于数组的开头，则再减一就会越界访问return obj->tail == 0 ? obj->arr[obj->k] : obj->arr[obj->tail - 1];//利用三目操作符则就可以巧妙解决ptrail处于数组开头的情况}
}void myCircularQueueFree(MyCircularQueue* obj) 
{obj->arr = NULL;obj->head = 0;obj->tail = 0;obj->k = 0;free(obj);obj = NULL;
}

结束语

      到此数据结构栈和队列的队列部分也就讲解完了，所以栈和队列整个板块也就全部讲解完了。难度上的话其实没有前面的顺序表和链表高，主要还是栈以及队列是在一些特殊的场景进行利用，原因就在于两者的数据插入删除都受到了限制，但这不影响栈和队列在数据结构中的地位，所以也是需要好好消化吸收的。而后面我就要为大家讲解数据结构中的二叉树了，希望本篇文章能对大家学习数据结构有所帮助！