【第二十周】机器学习笔记09

摘要

这周系统学习了机器学习模型评估与优化的核心方法。通过引入交叉验证集，我理解了如何公正地评估模型性能并自动选择最佳模型。偏差和方差的诊断让我能准确判断模型是欠拟合还是过拟合，而学习曲线则揭示了数据量对模型表现的影响。正则化参数λ的调节和人类表现基准的建立，为模型优化提供了具体方向。这些知识构成了一个完整的模型调试框架。

Abstract

This week’s learning focused on fundamental techniques for machine learning model evaluation and optimization. The introduction of cross-validation sets provided a fair approach to assess model performance and automate model selection. Diagnosing bias and variance helped identify underfitting vs. overfitting issues, while learning curves revealed how dataset size affects performance. Regularization parameter tuning and establishing human-level performance benchmarks offered concrete optimization pathways. These elements form a comprehensive framework for systematic model debugging and improvement.

一、模型选择和训练交叉验证测试集

在上一周中，我们看到了如何使用测试集来评估模型的性能，在本周中，让我们对这个想法进一步优化，它可以让我们使用一种技术，自动选择一个合适的机器学习算法的模型

我们看到的一件事，一旦模型的参数W和B适配了训练集，训练误差可能并不是很好地指示算法的表现，或者算法对新数据的泛化能力如何在训练集中没有出现的样本

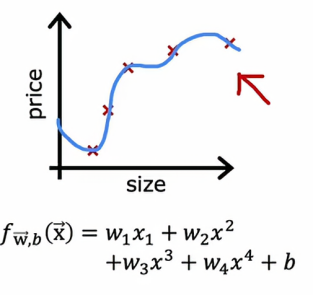
特别是对于这个例子而言，这可能远低于实际的泛化误差，我的意思是指那些不在训练集中的新样本上的平均误差，我们在上一节中看到的是Jtest算法在未训练样本上的表现，这将更好地指示模型在新数据上的表现状况，当然是训练集之外的其他数据，让我们看看这如何影响我们使用测试集来为特定机器学习选择模型应用

如果我们在拟合一个函数来预测房价或解决其他回归问题，我们可能会考虑的一种模型是拟合像这样的线性模型

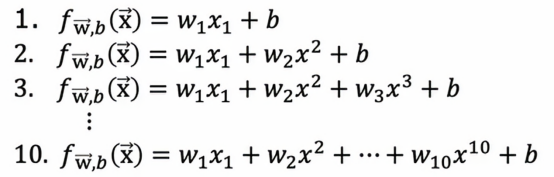
在这个例子中，我们将用d=1来表示拟合一个一阶多项式，d=2即来表示拟合一个二阶多项式，以此类推，最终到d=10，如果我们用这样的模型拟合到我们的训练集，我们会得到一些参数w和b，然后我们可以计算Jtest来估计这个模型在新数据上的泛化效果，我们可以查看从d=1到d=10，哪个Jtest值最低，假设我们发现五阶多项式的Jtest是最低的，那么我们可以认为五阶多项式d=5最优，并选择该模型应用于我们的模型，如果我们想要评估这个模型的表现，我们可以做的是报告测试集误差Jtest w5 b5。

这个程序有缺陷的原因是Jtest对于w5 b5可能是一个乐观的泛化误差估计，换句话说，它可能低于实际的泛化误差，原因是，我们在上面讨论的程序中，我们实际上拟合了一个额外的参数，即d多项式的度数，并使用测试集选择了这个参数，所以在前面，我们看到如果我们将wb拟合到训练集数据上，那么训练数据会对泛化误差产生过于乐观的估计，结果也是，如果我们使用测试集选择参数d，那么测试集Jtest现在也是过于乐观的，也就是说低于泛化误差的实际估计，因此，这一页上的程序是有缺陷的。

相反，如果我们想自动选择一个模型，比如决定使用哪个阶数的多项式，我们有一些修改和测试程序以进行模型选择的方法，通过在不同模型的选择

现在，让我们把原来的数据集分为三个部分，原来我们是分了两个部分

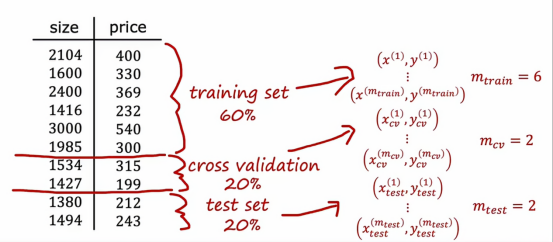
百分之60是训练集，用来训练模型，百分之20是交叉验证样本，用于使用这20的数据集来交叉检查有效性或不同模型的准确性，百分之20是测试集，用来评估模型的优劣

所以拥有这三个数据子集，训练集、交叉验证集、测试集，我们可以计算训练误差、交叉验证误差和测试误差，使用这三个公式，通常这些术语都不包括正则化项，正则化只包含在训练目标中

而中间这个新术语，交叉验证误差，只是我们交叉验证例子的平均值，例如平方误差，而这个术语，除了叫交叉验证误差，也简称为验证误差。

掌握了这三个学习算法性能的衡量标准，我们就可以进行模型选择了，让我们回到之前谈论的情况

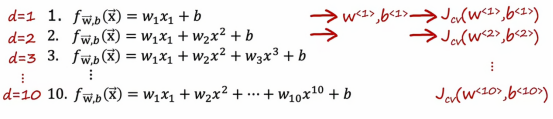
我们把误差换为交叉验证误差，我们现在验证的是看哪个模型有最低的交叉验证误差，假设当d=4时，交叉验证误差是最小的这意味着我们会选择这个四阶多项式作为你在这个应用中使用的模型，最后，如果我们想报告这个模型在新数据上的泛化误差估计，我们应该用第三个数据子集测试集并报告w4的Jtest，我们会注意到在整个过程中，我们用训练集来拟合这些参数，然后我们使用交叉验证集选择参数d或选择多项式的阶数，直到这一点，我们还没有拟合任何参数，这就是为什么在这个例子中Jtest会是对这个模型的泛化误差的公平估计，所以这提供了一种更好的模型选择程序，它可以让我们自动决定为线性回归模型选择什么阶数的多项式，这种模型选择程序同样适用于其他类型的模型选择

1、新奇角度的理解

一开始，我对这理解不来，直到我看到视频弹幕中有人举了几个例子，感觉豁然开朗了，
他说：“训练集、交叉训练集、测试集就好比考试学习，训练集就是平时老师上课讲的书本上的例题或者是课后作业上的习题；而交叉训练集是我们在校外买的模拟卷，模拟考试时的情况；而测试集就是高考，里面的题目我们都没有见过，需要通过我们平常从习题中学习的方法去解决高考中遇到的题目。”

还有一个角度的看法，有人说：“为什么加了交叉验证集，模型输出结果才是公正且不怎么乐观的？就好似我们先和一个人讨论做出决定，然后让第三个人评估，这样的结果公正合理。如果参与评估的人参与了决策，那么这个结果就不那么公平客观合理了。”

总而言之，训练集和交叉验证集用来选择模型，确定模型之后才使用测试集。

二、偏差诊断和方差

开发机器学习系统的典型工作是我们有一个想法，我们几乎总会发现它的效果没你期待的那么号，所以构建机器学习系统的关键是如何决策接下来做什么，以提高其性能。

让我们回顾一下第一次上课举的例子

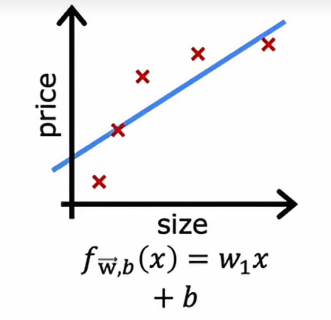
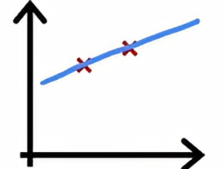
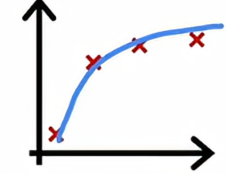
给定这个数据集，如果我们用一条直线拟合它，效果并不好，我们说这个算法有高偏差，或者它对这个数据集欠拟合，如果我们用四阶多项式拟合

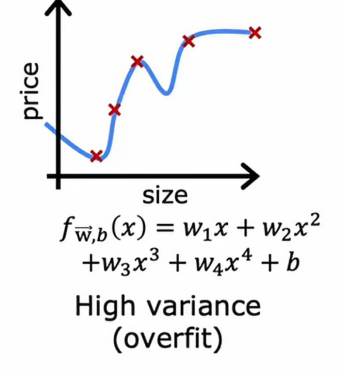
那么它有高方差，或者说它过拟合

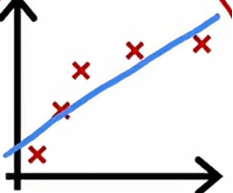
如果我们用二次多项式拟合

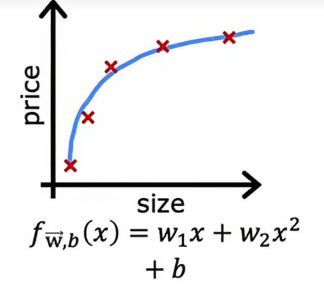
效果看起来相当不错，我们说这样刚刚好，因为这是一个只有单个特征x的问题，我们可以绘制函数f并像这样查看它，但如果我们有更多特征，我们无法绘制f并轻松可视化它是否表现良好，所以与其试图查看这样的图，更系统的方法来诊断或找出你的算法是高偏差还是高方差是查看我们的算法在训练集和交叉验证集上的表现

以上面欠拟合的情况为例，如果我们计算jtrain，算法在训练集上的表现如何呢，答案是表现并不好，所以我会说Jtrain在这里会很高，因为示例和实际之间存在相当大的错误，因此如果我们有一些新的例子Jcv，这些是算法以前没见过的样子，表现同样不好，所以Jcv也会很高，所以可以看出，高偏差的模型具有一个普遍的特征就是它在训练集上的表现不好

让我们再看向过拟合的情况为例，如果我们计算Jtrain，Jtrain会很低，说明它在训练集上表现的相当不错，非常适合训练数据，但是如果我们在训练集中没有出现过的其他例子上评估这个模型，那么我们会发现Jcv会很高，因此高方差的典型特征就是Jcv很高，高于Jtrain，换句话说，它在见过的数据上表现得比在没见过得数据上好得多

所以我们所作得重点就是通过计算Jtrain和Jcv看看Jtrain是否高或Jcv是否远高于Jtrain，这给了我们一种灵感，即使我们无法绘制出函数f，也能判断出我们的算法是高偏差还是高方差

最后我们再来看下最后一个情况，我们发现，在这种情况下，Jtrain和Jcv都很低，这说明它不仅在训练集上的表现良好、它在交叉训练集上的表现也很好，这说明该模型不仅能够很好的拟合现有的数据，也能很好地拟合之后从未出现过的数据

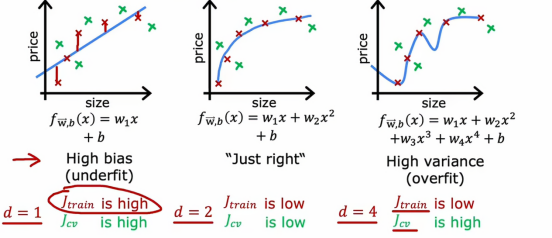
1、d值与Jcv和Jtrain的关系

我们再画一张图，其中图的横轴是我们拟合到数据的多项式的阶数，左边对应的是较小的d值，右边对应的是较大的d值，所以如果我们要绘制Jtrain作为多项式阶数函数的图像

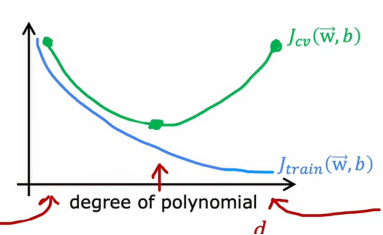
Jcv代表的是交叉训练集的误差，依据上面我们分析的三张图，我们发现，在d很小的时候，Jcv很大，说明算法不能很好低拟合之前没见过的新数据，但是当d很大的时候，Jcv也很大，解释的原因是因为这个算法过于拟合现有的数据，导致我们不能很好地推广到新数据当中，而直到d不大也不小的时候，Jcv才达到最小值，这也就是为什么，我们例子当中的二次多项式有着最小的Jcv和较小的Jtrain，这样的性能才是最好的

总结一下，如何诊断学习算法中的偏差和方差，如果我们的学习算法有高偏差或欠拟合数据，关键指标是Jtrain很高，这对应曲线的最左边，且通常Jtrain和Jcv很接近，高方差的关键指标是Jcv远大于Jtrain，即曲线最右边，实际上，还可能出现高偏差和高方差同时出现的情况，它的表现是Jtrain会很高并且Jcv会远大于Jtrain

三、正则化与偏差和方差

在上一个小节中，我们看到不同的多项式d如何影响模型的偏差和方差，在本节中，让我们看看正则化如何影响，特别是正则化参数λ的选择如何偏差和方差，因此影响整个算法的性能

在这个例子中，我们将使用一个四阶多项式，但我们会使用正则化来拟合这个模型

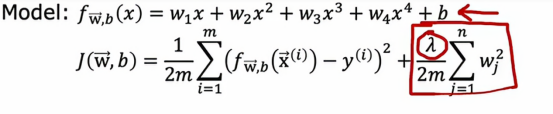
但这里的λ是控制我们在保持参数w小与拟合训练数据好之间权衡的正则化参数

让我们从将λ设置一个非常大的值开始

1、当λ很大时

如果我们设置λ = 10000时，我们会得到一个这样的图

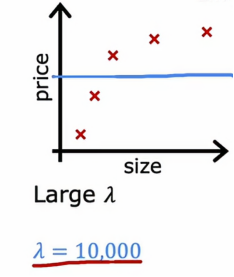
因为如果λ非常非常大，那么算法会非常倾向于保持这些参数w非常小，这样的话，w1、w2、w3、w4都几乎为0，所以该函数就近似于常数b，这就是为什么是图片上表现的常函数，这个模型很明显有很高的偏差，并且对数据欠拟合

2、当λ很小时

如果我们设置λ = 0，我们会得到一个这样的图

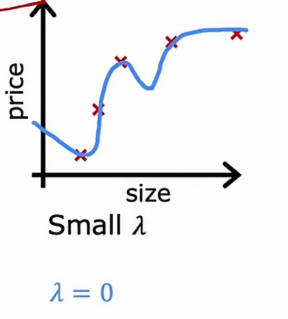
其实就相当于没有正则化参数，跟之前的图没有任何区别，它表现出的时高方差和过拟合

3、合适的λ值

如果我们选择了一个较为合适λ值（合适的λ值是根据具体情况去界定的），那么图看起来是这样的

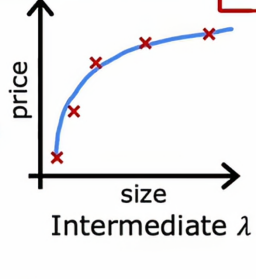
这样既能很好地拟合数据同时Jtrain和Jcv都很小

所以如果我们在决定使用什么样的λ作为正则化参数，交叉验证提供了一种方式，让我们看看怎么做，需要提醒的是，我们现在正在解决的问题是，如果我们在拟合一个四次多项式，并且我们正在使用正则化，这将类似与我们使用交叉验证选择多项式阶数d的程序

四、建立表现基准

让我们看一些具体的例子，来判断Jtrain和Jcv如何判断一个学习算法，这次让我们把目光放到语音识别上

我们让用户有时候可以用语音输入，这样我们得到训练失误的概率是10.8％，这说明机器有10.8%概率判断失败，并且我们还要测量语音识别算法在单独的交叉验证集上的表现，假设它的错误率是14.8%，乍一看感觉机器的出错的概率好像还很高，但是实际上人类出错的概率为10.6%，我们发现人和机器的差别好像很小，在现实生活中，如果训练误差和人类现有水平差别不大的话，就说明机器在方面表现还是出色的，但是这里我们发现一个问题，就是Jcv和Jtrain的差距很大，按照我们上一节的知识来判断，这应该属于的时方差问题而不是偏差问题

所以判断训练误差是否偏高时，通常建立一个基线水平的表现是有用的，通俗来说，就是我们合理期望我们的学习算法最终达到的错误水平是多少，一种常见的办法就是测量人类在这项任务上表现有多好，因为人类非常擅长理解语音数据，另一种估算基线方法看看是否有一些竞争算法，可能是别人实现过的早期版本或者现有版本。

当我们评估一个算法是否有高偏差或高方差时，我们可以查看基线水平的表现，测量的两个关键量是训练误差与基线水平之间的差异，然后我们还要看训练误差和交叉验证误差之间的差距。

五、学习曲线

学习曲线可以帮助我们理解学习算法在不同数据量下的表现

让我们绘制一条拟合二次多项式函数模型的学习曲线，我会绘制Jcv、交叉验证误差，以及Jtrain训练误差，在这张图上，横轴表示m，即训练集的大小，或者是算法可以学习的示例数量，纵轴是误差，即Jcv或Jtrain，它看起来是这样的

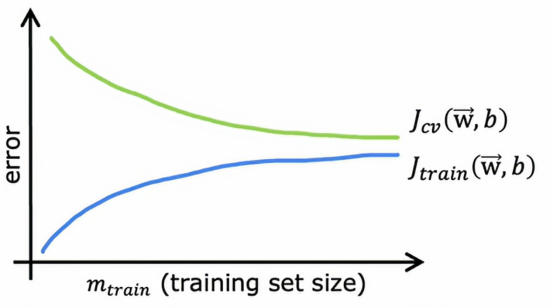
Jcv随着训练集大小变大而变小，Jtrain随着训练集大小变大而变大

我们从只有一个训练样本的例子开始，如果我们用二次模型来拟合这个数据，我们可以轻松拟合一条直线或曲线，你的训练误差将为0

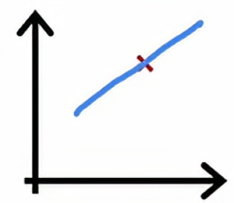
当有两个训练样本的时候，我们可以再次拟合一条直线，并实现零训练误差，事实上，如果我们有三个训练样本，二次函数依然可以很好地拟合，并几乎达到零训练误差

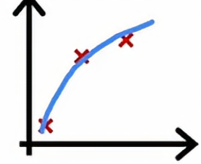
‘当我们有四个样本的时候，要完美拟合这四个样本会稍微有点困难一些，我们可能会得到一个看起来像这样的曲线，总体拟合得不错，但在某些地方稍微有点误差。

当我们有五个训练误差时候，我们仍然可以适当拟合，但要完美拟合所有样本会更难一点。

所以当我们逐步增大训练集，要完美拟合每一个训练样本将会变得越来越困难，交叉验证误差通常会比训练误差更高，因为我们是对训练集拟合参数，因此肯定是期望在训练集上至少有一点点更好，或者当m很小得时候，甚至可能在训练集上比交叉验证集好很多。

现在让我们看看高偏差与高方差的学习曲线是什么样子，我们先从高偏差或欠拟合的情况开始，回想高偏差的例子，是用线性函数拟合了一个看起来像这样的函数

如果我们要绘制训练误差，那么训练误差将会像这样上升，就像我们预期的那样，事实上，这条训练误差曲线可能会开始变平，我们称之为平台，这意味着经过一段时间会变平，这是因为当我们获得越来越多的训练样本时，在拟合简单的线性函数时，我们的模型实际上不会发生太大的变化，它是在拟合一条直线，即使你获得更多更多样本，没有太多可以改变的，这就是为什么平均训练误差在一段时间后会趋平，同样的，我们的交叉验证误差会下降，而且经过一段时间后会趋平，这就是为什么Jcv再次要高于Jtrain，因为我们即使获得越来越多的样本，我们拟合的直线不会有太多改变，这个模型太简单不适合那么多的数据，这就是为什么这两个曲线Jcv和Jtrain会在一段时间后趋平

如果我们有一个基准性能的衡量标准，比如人的水平表现

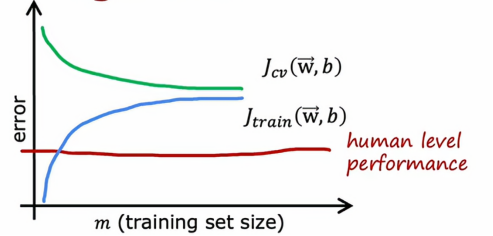
那么它的值可能会低于我们的Jtrain和Jcv，所以人的水平表现可能是这样的，基准性能和Jtrain之间有一个很大的差距，这是我们判断这个算法具有高偏差的指标，也就是说，如果我们能够拟合一个比直线更复杂的函数，预期会有更好的表现

那么现在如果我们延长x轴，也就是增大训练集的大小，Jcv和Jtrain始终会保持这个近似于水平的样子，所以这就得出一个结论，如果一个学习算法有高偏差，增加太多的数据本身页帮不了什么忙，我们的固有思维都是认为，只要我们的数据足够的多，算法的表现就会越好，但如果我们的算法有高偏差，那么我们只是增加更多的训练数据，也不会降低错误率很多，这就是问题所在，无论再添加多少示例，简单的线性组合也不会有太大的改善，这就是为什么在投入大量精力收集更多的训练数据之前，我们得检查我们的学习算法是否有高偏差

让我们看看高方差的学习算法曲线长什么样

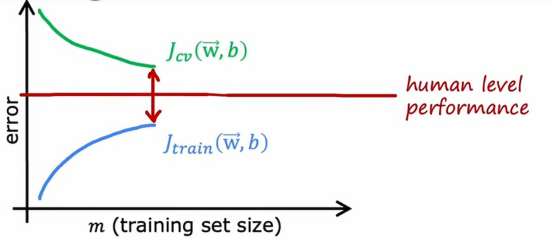
由上图可以看出，它在训练集上的表现远好于交叉验证集上的表现，如果我们绘制一个基准性能水平，它会出现在这里，这就表明，Jtrain有时候可能高于人类水平表现，我们可能对训练集拟合的非常好，从而使误差低得不切实际，例如在这个例子里误差为0

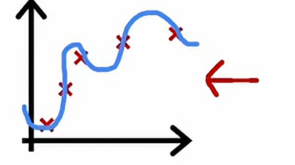
这实际上比人类预测房价得能力还要好，但同样，高方差得信号使Jcv是否远高于Jtrain，当我们有高方差时，增加训练集得大小可能会有很大得帮助，比如我们将图像往右推，会得到这样得图像

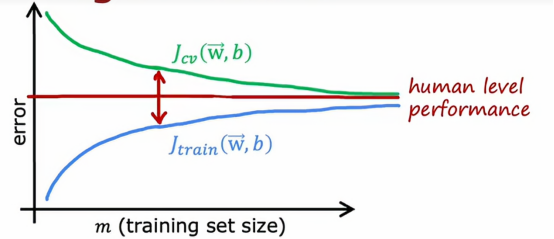
这样只需增加训练集得大小就可以降低交叉验证误差，使我们得算法性能越来越好

六、再次决定下一步做什么

专业程序员会经常查看训练误差和交叉验证误差，以判断算法是否具有高偏差或高方差，事实证明，这将帮助我们做出更好得决定，知道下一步该干什么，以提高我们算法的性能，

我们来看一个例子，当我们的算法出现高偏差的时候，我们一般会这么几个处理手段：

·尝试设置更多的特征
·增加多项式特征
·减少λ的值

如果出现高方差，那么有以下几个处理手段：

·获取更多的训练样本
·设置更少的特征
·增大λ的值

总结

这周的学习让我对机器学习模型调优有了体系化的认识。最重要的收获是理解了训练集、验证集、测试集的真正分工——就像学习过程中课本、模拟考和高考的关系，验证集让模型选择变得客观可靠。通过J_train和J_cv的对比分析，我现在能准确判断模型问题：高偏差时两者都高，高方差时差距大。学习曲线特别有启发，它告诉我高偏差时加数据没用，高方差时加数据才有效。正则化参数λ的调节就像给模型加上"刹车"，λ太大导致欠拟合，λ太小导致过拟合。人类表现基准的引入让我明白了如何设定合理的目标。这些知识让我不再盲目调参，而是能够系统诊断问题并采取针对性措施，真正掌握了机器学习模型优化的科学方法。