人工智能之数学基础：随机变量函数的分布（离散和连续）

本文重点

随机变量的分布（离散型随机变量的分布、连续型随机变量的分布）我们已经了解了，本文我们将更近一步，学习随机变量函数的分布。简单来说就是设随机变量X的分布已知，求Y=g(X)的分布。

随机变量函数是以随机变量为自变量的函数，它将一个随机变量映射成另外一个随机变量，这两个随机变量一般是不同的分布。

两种

这里分为两种，一种是离散型随机变量函数的分布，另外一种是连续型随机变量函数的分布。

离散型随机变量函数的分布

某城市一个月内发生火灾的次数 X～P(5),试求随机变量Y=|X-5|的概率分布。

解答：

X的分布已经知道了，就是泊松分布，通过如下的方式来表示：

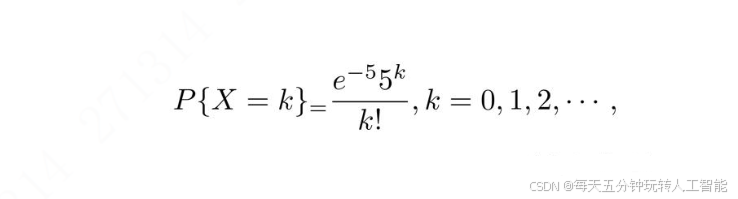
由于Y=|X-5|,所以X=5+Y和X=5-Y（时刻保证X为0和正数，因为火灾次数一定不能是负数）

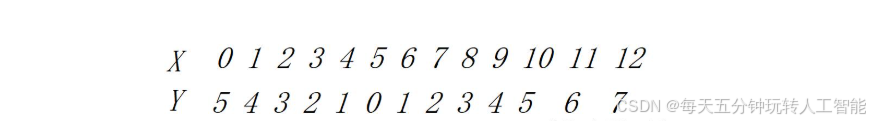
如上所示，我们可以看到当Y=1，2，3，4，5（X=5-i和X=5+i）的时候是由两个概率相加的，于是Y的分布概率分布为：