QLoRA基础知识和微调原理学习

说明

• 文章内容学自网络，仅供学习和交流使用，最终著作权归原作者所有！

背景

• 随着大语言模型(LLM)的规模不断扩大，微调这些模型需要大量的计算资源和显存。传统的微调方法在处理超大模型时，显存需求和计算成本都非常高。
• LoRA：通过低秩分解减少了可训练参数，但仍需加载完整的模型权重到GPU显存中。假设你想微调一个65B参数的大模型：传统方法需要500GB+ GPU显存；LoRA方法仍需要130GB GPU显存(因为要加载原始模型)；QLoRA方法只需要48GB GPU显存。
• LoRA虽然减少了可训练参数，但原始模型权重仍需完整加载到GPU。对于超大模型来说，光是加载就需要太多显存。

一 基础概念

1.1 量化基础概念

• 量化是将高精度的数值（如浮点数）转换为低精度的数值（如整数）的过程，以减少存储和计算的需求。它可以显著降低模型的显存占用和计算复杂度，同时在某些情况下还能加速推理过程。

注意：只能从高精度量化到低精度，不能反向操作。
FP32 -> FP16 -> 8-bit -> 4-bit

1.2 精度基础概念

1.2.1 FP32 (32位浮点数)

FP32 是一种遵循 IEEE 754 标准的浮点数数据类型，广泛用于科学计算和图形学。
FP32 总共占用 32 位（4字节），其结构分为三个部分：

• 符号位: 1位，0 代表正数；1 代表负数。
• 指数位: 8位，可表示 0-255。使用 偏置表示法，偏置值为 127。实际指数 = 指数位的值 - 127。指数位为 10000000 (128)，则实际指数为 128 - 127 = 1。指数位为 01111110 (126)，则实际指数为 126 - 127 = -1。
• 尾数位: 23位，实际计算时，会在二进制小数点前 默认添加一个 1 (这被称为规格化形式)。

  [1位符号位][8位指数位][23位尾数位]
  

• 表示范围:
  • 最小正数: ±1.175494351 × 10⁻³⁸
  • 最大正数: ±3.402823466 × 10³⁸
• 精度: 约7位十进制数字。

---

• 浮点数的最终值由以下公式计算得出：值 = (-1)^符号位 × 2^实际指数 × 尾数
• 示例解析：3.14159 -> 0x40490FDB

1. 十六进制转二进制：0x40490FDB -> 0100 0000 0100 1001 0000 1111 1101 1011
2. 按位解析

   [0 | 10000000 | 10010010000111111011011]↑      ↑                    ↑
   符号位  指数位              尾数位
   (1位)   (8位)               (23位)
   

---

详细计算过程

1. 符号位: 0 -> 正数，所以 (-1)^0 = 1。
2. 指数位: 10000000 (二进制) = 128 (十进制)。实际指数 = 128 - 127 = 1。
3. 尾数位: 10010010000111111011011。实际尾数 = 1.10010010000111111011011 (二进制) ≈ 1.5707963...。
4. 最终值计算：值 = 1 × 2^1 × 1.5707963... = 3.14159265359...。

1.2.2 FP16 (16位浮点数)

• 结构：[1位符号位][8位指数位][7位尾数位]
• 特点：保持与FP32相同的指数范围，牺牲一些精度换取更小的存储空间，常用于深度学习训练。

---

表示范围：

• 最小值：±6.10352 × 10^-5
• 最大值：±65504
• 精度：约3-4位十进制数字

  3.14159265359 -> 0x4049
  3.14159265359 -> 0x4248
  

1.2.3 INT8 (8位整数)&INT4 (4位整数)

• 结构：8位整数值。表示范围：有符号：[-128, 127]、无符号：[0, 255]。
• 量化示例：
  原始值: 3.14159265359
  量化后: 25 (假设映射到0-255范围)
• 需要额外存储：scale (缩放因子)，zero_point (零点偏移)。

---

• 结构：4位整数值
• 表示范围：有符号：[-8, 7]，无符号：[0, 15]
• QLoRA的NF4格式：特殊的非线性量化区间，[-1, -0.7, -0.3, -0.1, 0, 0.1, 0.3, 0.7, 1]。

1.2.4 精度对比示例&使用场景建议

原始值: 3.14159265359FP32: 3.14159265359  # 完整精度
BF16: 3.141          # 3位精度
FP16: 3.1416         # 4位精度
INT8: 3.14           # 2位精度
INT4: 3.0            # 1位精度# 存储同一个数所需的位数
FP32: 32位 -> 0x40490FDB
BF16: 16位 -> 0x4049
FP16: 16位 -> 0x4248
INT8: 8位  -> 25
INT4: 4位  -> 7

# 科学计算，需要高精度
使用FP32# 模型训练
使用BF16/FP16
- BF16: 训练更稳定
- FP16: 精度稍好# 模型推理
使用INT8/INT4
- INT8: 常规部署
- INT4: 资源受限场景# QLoRA训练
基座模型: INT4(NF4)
LoRA层: FP16

1.3 量化误差与舍入方式

1.3.1 量化误差

# 假设我们有一个FP16的权重值
原始值 = 0.37# 使用4-bit量化，我们只能用16个数字表示所有可能的值
可用的量化值 = [-1.0, -0.7, -0.3, -0.1, 0, 0.1, 0.3, 0.7, 1.0]# 0.37需要被映射到最近的可用值
量化后 = 0.3# 量化误差
误差 = 原始值 - 量化后的值= 0.37 - 0.3 = 0.07  # 这就是量化误差

1. 单个权重的误差可能很小weight_error = 0.07。
2. 但在前向传播时误差会累积。

layer1_error = weight_error * input_value
layer2_error = layer1_error * next_weight
...

3. 累积的误差可能导致：模型性能下降，训练不稳定，预测结果偏差。

---

1.3.2 QLoRA舍入方式

原始权重序列 = [0.37, 0.34, 0.36, 0.35]

1. 使用最近邻舍入
   • 传统结果 = [0.3, 0.3, 0.3, 0.3] # 所有值都被舍入到0.3
   • 问题: 完全丢失了原始分布信息
2. 使用随机舍入
   • QLoRA结果可能是 = [0.3, 0.3, 0.7, 0.3]
   • 优势：在统计意义上保持了原始分布，避免了系统性偏差，有助于训练稳定性。

这种设计的优势：

1. 保持统计特性：随机舍入帮助保持权重分布
2. 避免累积误差：减少系统性偏差
3. 训练稳定性：更好的梯度流动
4. 显存效率：在极致压缩的同时保持模型性能

1.4 量化校准

• 量化校准就是在压缩前，先分析数据特点，找到最合适的压缩方案。

# 假设有一层神经网络的权重
weights = [0.001,  # 接近0的小权重0.002,0.003,0.3,    # 中等大小的权重0.5,0.7,0.95,   # 接近1的大权重0.98
]# 不进行校准的4-bit量化
# 简单地平均分割0-1的范围为16份
简单量化结果 = [0.0,    # 小值都变成00.0,0.0,0.3,0.5,0.7,0.9,    # 大值的细微差别也丢失0.9
]# 经过校准的4-bit量化
# 根据权重分布设计量化点
校准后结果 = [0.001,  # 保留小值0.002,0.003,0.3,0.5,0.7,0.95,   # 保留大值的差别0.98
]

• 校准过程示例

# 1. 先看看数据的分布特点
def analyze_weights(model):weights = model.get_weights()return {"最小值": min(weights),"最大值": max(weights),"平均值": mean(weights),"分布集中区间": find_main_range(weights)}# 2. 根据分布特点调整量化方案
def calibrate_quantization(analysis):if "大部分值集中在0附近":return use_dense_zero_quantization()elif "值比较分散":return use_uniform_quantization()else:return use_custom_quantization()

• 校准的作用

校准的好处：1. 保留重要信息
原始值: [0.001, 0.002, 0.003]
未校准: [0.0, 0.0, 0.0]     # 信息丢失
已校准: [0.001, 0.002, 0.003] # 保留差异2. 减少量化误差
原始值: [0.98, 0.99, 1.0]
未校准: [1.0, 1.0, 1.0]    # 误差大
已校准: [0.98, 0.99, 1.0]  # 误差小3. 提高模型精度
- 更准确的权重表示
- 更好的模型性能

二 QLoRA相关的基础概念

2.0 QLoRA主要的内容

以下是QLoRA核心内容的表格总结，按您提供的结构整理：

模块	关键内容
量化基础
基本原理	通过降低数值精度减少模型存储和计算开销
精度格式	FP32（全精度）、FP16（半精度）、INT8/INT4（定点数）
量化误差	舍入误差与截断误差，受舍入模式（就近/向上/向下）影响
校准方法	动态范围统计（最大最小值/KL散度）确定缩放因子
QLoRA量化技术
NF4格式	基于正态分布的非均匀量化区间，优化神经网络权重分布保留
双量化	对量化缩放因子二次量化，减少额外参数存储（如INT8量化FP16的缩放因子）
显存管理机制
分页优化器	将临时张量换出到CPU内存，GPU显存不足时自动分页交换

• NF4优势：相比INT4，在相同比特数下对权重分布拟合更优，尤其适合正态分布特征的模型参数。
• 双量化效果：典型配置下可使显存占用再降低30%-50%，适用于超大模型微调。
• 分页优化器：类似操作系统虚拟内存机制，需注意CPU-GPU数据传输可能带来的延迟。

2.1 NF4量化

NF4的核心创新在于：

1. 非线性量化点分布
2. 针对神经网络权重的正态分布特性优化
3. 在相同位宽(4-bit)下获得更好的量化效果
4. 特别适合大语言模型的权重分布特征

# 传统4-bit整数量化(INT4)
INT4_POINTS = [-8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]
# 特点：线性均匀分布# QLoRA的NF4量化
NF4_POINTS = [-1.0, -0.7, -0.3, -0.1,   # 负值区间0,                         # 零点0.1, 0.3, 0.7, 1.0        # 正值区间
]
# 特点：非线性分布，针对正态分布优化
1. 在常见值（接近0）的地方放更多的量化点
2. 在罕见值（远离0）的地方放较少的量化点

# 神经网络权重通常呈现正态分布"""大多数权重集中在0附近|         ***          ||       *******        ||     ***********      ||  ******************  |-1 ------0------ +1"""# 传统INT4的问题"""1. 线性间隔不适合正态分布2. 对中心区域(接近0)的精度不够3. 对两端的大值表示过多"""

2.1.1 NF4的设计原理

class NF4Quantization:def __init__(self):# 1. 非均匀量化点设计self.quant_points = {"near_zero": [-0.1, 0, 0.1],     # 密集采样"middle": [-0.3, 0.3],           # 中等间隔"far": [-1.0, -0.7, 0.7, 1.0]    # 大间隔}def quantize(self, weight):# 2. 基于距离的量化if abs(weight) < 0.15:# 小值使用精细量化return find_nearest(weight, self.quant_points["near_zero"])elif abs(weight) < 0.5:# 中等值使用中等精度return find_nearest(weight, self.quant_points["middle"])else:# 大值使用粗略量化return find_nearest(weight, self.quant_points["far"])

2.1.2 NF4与传统量化的对比

NF4的核心创新在于：

1. 非线性量化点分布
2. 针对神经网络权重的正态分布特性优化
3. 在相同位宽(4-bit)下获得更好的量化效果
4. 特别适合大语言模型的权重分布特征

# 假设有以下权重
weights = [0.05, 0.2,0.28 , 0.8, -0.03, -0.6, -0.9]# INT4量化（线性）
def int4_quantize(weights):# 均匀分布的量化点quantized = [0.0,   # 0.05  -> 00.25,  # 0.2   -> 0.250.25,  # 0.28   -> 0.250.75,  # 0.8   -> 0.750.0,   # -0.03 -> 0-0.5,  # -0.6  -> -0.5-1.0   # -0.9  -> -1.0]return quantized# NF4量化（非线性）
def nf4_quantize(weights):# 非均匀分布的量化点quantized = [0.1,   # 0.05  -> 0.1 (更精确)0.3,   # 0.2   -> 0.30.3,   # 0.28   -> 0.30.7,   # 0.8   -> 0.70.0,   # -0.03 -> 0 (更精确)-0.7,  # -0.6  -> -0.7-1.0   # -0.9  -> -1.0]return quantized

2.1.3 NF4的优势

• 精度优化：在零点附近采用更密集的量化点，提升小数值范围的精度。 在大值区域通过优化分布，确保数值表示的合理性。
• 显存效率：位宽保持4-bit，确保显存占用高效。 表示范围优化为[-1,1]区间，提升数值覆盖能力。
• 训练稳定性 ：梯度传播设计兼顾数值稳定性，减少训练波动。舍入误差控制更严格，降低误差累积对训练的影响。

2.2 双量化技术

1. 双量化就是"量化两次"：第一次，把权重量化成4-bit；第二次，把量化参数(scale)量化成8-bit。
2. 主要目的：减少量化参数占用的显存，原本16-bit的scale变成8-bit。
3. 最终效果：权重用4-bit存储，量化参数用8-bit存储，进一步节省了显存空间。

---

2.2.1 单量化的缺陷和双量化的来源

1. 首先理解单次量化

# 假设我们有一组原始权重
original_weights = [2.5, -1.8, 0.4, -0.2, 0.1]# 单次量化过程
def single_quantization():# 1. 计算量化参数scale = max(abs(original_weights))  # = 2.5# 2. 归一化normalized = [2.5/2.5,   # = 1.0-1.8/2.5,  # = -0.720.4/2.5,   # = 0.16-0.2/2.5,  # = -0.080.1/2.5    # = 0.04]# 3. 使用NF4量化quantized = [1.0,    # 1.0 -> 1.0-0.7,   # -0.72 -> -0.70.1,    # 0.16 -> 0.1-0.1,   # -0.08 -> -0.10.0     # 0.04 -> 0.0]# 需要保存：# - 量化后的权重(4-bit)# - scale值(FP16格式，16-bit)

2. 双量化的问题又来

# 问题：scale值占用空间太大
def memory_analysis():# 对于每个权重：weight_memory = "4-bit"      # 量化后的权重scale_memory = "16-bit"      # 量化参数(scale)# 显存占用比例print("scale占用显存是权重的4倍！")# 例如：# 权重：[1.0, -0.7, 0.1, -0.1, 0.0] -> 4-bit每个数# scale：2.5 -> 16-bit

3. 双量化的解决方案

def double_quantization():# 第一次量化：对权重进行4-bit量化# 1. 计算scalescale = 2.5# 2. 量化权重quantized_weights = [1.0, -0.7, 0.1, -0.1, 0.0]  # 4-bit# 第二次量化：对scale进行8-bit量化# 3. 量化scale值quantized_scale = quantize_to_8bit(2.5)# 最终存储：# - 量化后的权重(4-bit)# - 量化后的scale(8-bit，不是原来的16-bit)

2.2.2 具体例子

def full_double_quantization_example():# 原始权重weights = [2.5, -1.8, 0.4]# 1. 计算scalescale = max(abs(weights))  # = 2.5# 2. 第一次量化（权重）normalized = [w/scale for w in weights]# normalized = [1.0, -0.72, 0.16]# 使用NF4量化点quantized_weights = [1.0, -0.7, 0.1]  # 4-bit存储# 3. 第二次量化（scale）# 直接线性量化到8-bitquantized_scale = int(scale * 255 / 256)  # 8-bit存储

2.2.3 两种量化方式的区别

特性	第一次量化（NF4）	第二次量化（线性）
量化方式	映射到预定义非线性分布的量化点	简单线性映射均匀分布
位数	4-bit	8-bit
主要目的	保持权重分布特征	压缩存储空间
关键设计原因	权重分布需特殊处理 模型性能对精度敏感	scale为单值无需特殊分布 8-bit足够精度 实现简单快速
案例	权重：1000个 × 4-bit = 4000 bits scale：1个 × 16-bit = 16 bits 总计：4016 bits	权重：1000个 × 4-bit = 4000 bits scale：1个 × 8-bit = 8 bits 总计：4008 bits

2.3 分页优化器

• 传统方式模型参数在GPU，优化器状态也在GPU。Adam优化器需要存储两倍于参数量的状态。对于大模型来说，GPU显存不够用。例如：

model_params = "1GB参数"
adam_states = "2GB优化器状态"  # 需要常驻GPU
total_gpu_memory = "3GB"    # 总共占用

• 分页优化器核心思想：优化器状态主要存在CPU显存中，只把当前需要用的部分调到GPU，用完就调回CPU，释放GPU显存。例如：处理一个神经网络层，把这层的优化器状态从CPU调到GPU，更新这层的参数，把更新后的状态调回CPU，GPU显存被释放。

---

具体例子

# 假设我们有一个大模型
model = {"layer1": "1GB参数","layer2": "1GB参数","layer3": "1GB参数"
}

传统优化器会将所有优化状态保存在GPU显存中：

gpu_memory = {"layer1_state": "2GB","layer2_state": "2GB","layer3_state": "2GB"
}
# 总计需要6GB GPU显存

分页优化器采用逐层处理策略：

# 处理layer1时
gpu_memory = {"layer1_state": "2GB"  # 仅加载当前层状态
}
# 处理完成后释放# 处理layer2时
gpu_memory = {"layer2_state": "2GB"  # 替换为第二层状态
}
# 处理完成后释放# 处理layer3时
gpu_memory = {"layer3_state": "2GB"  # 替换为第三层状态
}
# 处理完成后释放

该方法通过分时复用显存空间，将峰值显存需求从6GB降至2GB，适用于显存受限的设备环境。注意实际实现时需要处理状态切换时的数据持久化问题。

项目	传统优化器	分页优化器
模型参数	1GB	1GB
优化器状态	2GB	0.1GB（动态保留部分）
总GPU显存	3GB	1.1GB
特点	常驻显存	动态调度

简单来说：

1. 传统优化器就像是把所有书都摊在桌子上
2. 分页优化器就像是：书架上放着所有的书（CPU显存），桌子上只放当前在看的那本书（GPU显存），看完一本就放回书架，再拿下一本，这样桌子（GPU显存）就不会被占满。

三 QLoRA微调方式

3.1 Full Finetuning&Lora&QLora对比

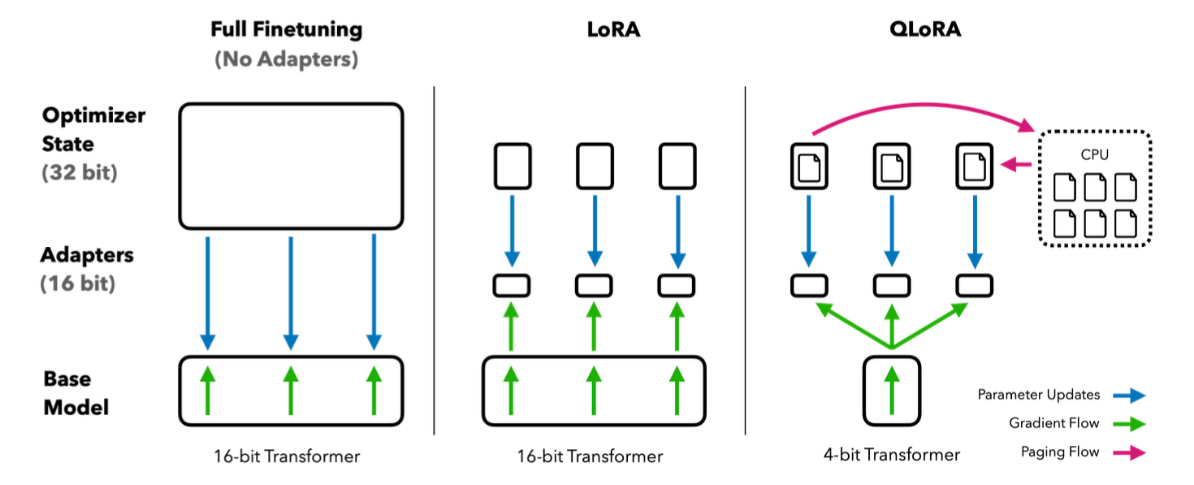
1. Full Finetuning (完全微调)

• Base Model: 16-bit基础模型，没有使用适配器(No Adapters)。
• Optimizer State: 需要存储所有参数的32-bit优化器状态。
• 特点：需要更新所有模型参数，显存消耗最大。

---

2. LoRA (低秩适配器)

• Base Model: 16-bit基础模型。
• Adapters: 添加16-bit低秩适配器。
• 特点：基础模型参数保持冻结，只训练适配器参数，每个层都有独立的适配器。

---

3. QLoRA (量化版LoRA)

• Base Model: 4-bit量化基础模型
• Adapters: 添加低秩适配器
• 创新点：基础模型被量化到4-bit，使用分页优化器(CPU存储优化器状态)。

• 粉色箭头表示优化器状态在CPU-GPU间的分页流动
• 蓝色箭头表示参数更新流
• 绿色箭头表示梯度流

特性	Full Finetuning	LoRA	QLoRA
显存效率	显存消耗最大	中等显存消耗	显存消耗最小
参数更新	更新所有参数	只更新适配器参数	只更新适配器参数,且使用分页机制
模型精度	16-bit	16-bit	4-bit基础模型 + 32-bit适配器
优化器状态管理	全部在GPU	全部在GPU	CPU-GPU分页机制

3.2 QLoRA与LoRA的关系对比

• LoRA：主要通过低秩分解减少参数量，适用于中小型模型的高效微调。
• QLoRA：Q代表Quantization，即量化。QLoRA的核心创新在于结合量化技术来优化显存和计算效率，将模型权重从高精度(如FP16)转换为低精度(如4-bit)，大大减少资源占用，特别适合在消费级硬件上微调超大模型。QLoRA = LoRA + 量化技术，LoRA负责减少可训练参数，量化负责压缩原始模型权重。

3.3 LoRA与QLoRA工作方式对比

原始模型(FP16格式保持不变)
|    权重矩阵A (16-bit)    |
|    权重矩阵B (16-bit)    |    +    低秩矩阵(可训练)
|    权重矩阵C (16-bit)    |             ↑
|           ...           |         仅训练这部分

原始模型(量化为4-bit)
|    权重矩阵A (4-bit)     |
|    权重矩阵B (4-bit)     |    +    低秩矩阵(可训练)
|    权重矩阵C (4-bit)     |            ↑
|          ...            |         仅训练这部分

• 训练过程：LoRA和QLoRA都只训练低秩矩阵，原始模型权重都是冻结的，区别仅在于原始模型的存储格式。

3.4 QLoRA的优缺点

1. 提高显存效率：通过4-bit量化，QLoRA显著降低显存占用，可以在单个48GB GPU上微调65B参数模型（FP16格式：130GB；4-bit量化：32.5GB），甚至在24GB消费级GPU上微调33B参数模型。
2. 保持模型性能：创新的NF4量化格式，几乎不损失模型效果。量化后的模型推理速度更快，适合大规模部署。
3. 降低硬件门槛：减少对高端硬件的依赖，使得更多研究者和开发者能够参与大模型的微调。

---

1. 精度损失：量化可能导致一定的精度损失，尽管QLoRA通过NF4技术尽量减少了这种影响。
2. 复杂性增加：需要额外的量化和反量化步骤，增加了实现的复杂性。
3. 训练稳定性：需要仔细调节超参数以确保训练稳定性。