当前位置：首页 > news >正文

深度学习参数优化

news 2025/11/1 11:03:05

在这里插入图片描述

模型训练总遇瓶颈？掌握参数初始化、优化器等核心技巧，让你的模型收敛更快、性能更优！📌关注小编不迷路~

一、参数初始化

1.1 参数初始化的必要性

我们在构建网络之后，网络中的参数（主要是权重和偏置）需要初始化：

偏置一般初始化为 0 即可；
权重的初始化更关键，直接影响模型收敛性和性能

1.2 常见初始化方法

均匀分布初始化（📌推荐）
权重从区间 (-1/√d, 1/√d) 均匀随机取值（d 为神经元输入数量）
正态分布初始化
权重从 均值0、标准差1 的高斯分布中随机取样，用小值初始化
全0初始化（不推荐）
将所有权重参数初始化为 0
全1初始化（不推荐）
将所有权重参数初始化为 1
固定值初始化（不推荐）
将所有权重参数初始化为 指定固定值（如5、-2等)
Kaiming 初始化（HE 初始化）（📌推荐）
分为 正态分布 和 均匀分布 两种变体，针对ReLU等激活函数优化，缓解梯度消失
Xavier 初始化（Glorot初始化）
核心思想：让各层的激活值方差和梯度方差在传播中保持一致，分为正态分布和均匀分布两种

1.3 PyTorch API 实现示例

import torch
import torch.nn as nn

均匀分布随机初始化

def test01():linear = nn.Linear(5, 3)  # 输入维度5，输出维度3nn.init.uniform_(linear.weight)  # 均匀分布初始化权重print(linear.weight.data)

固定值初始化

def test02():linear = nn.Linear(5, 3)nn.init.constant_(linear.weight, 5)  # 权重固定为5print(linear.weight.data)

全0初始化

def test03():linear = nn.Linear(5, 3)nn.init.zeros_(linear.weight)  # 权重全0print(linear.weight.data)

全1初始化

def test04():linear = nn.Linear(5, 3)nn.init.ones_(linear.weight)   # 权重全1print(linear.weight.data)

态分布随机初始化

def test05():linear = nn.Linear(5, 3)nn.init.normal_(linear.weight, mean=0, std=1)  # 均值0、标准差1print(linear.weight.data)

Kaiming 初始化

def test06():# Kaiming 正态分布linear = nn.Linear(5, 3)nn.init.kaiming_normal_(linear.weight)  print(linear.weight.data)# Kaiming 均匀分布linear = nn.Linear(5, 3)nn.init.kaiming_uniform_(linear.weight)  print(linear.weight.data)

Xavier 初始化

def test07():# Xavier 正态分布linear = nn.Linear(5, 3)nn.init.xavier_normal_(linear.weight)  print(linear.weight.data)# Xavier 均匀分布linear = nn.Linear(5, 3)nn.init.xavier_uniform_(linear.weight)  print(linear.weight.data)if __name__ == '__main__':test07()  # 可替换为其他test函数（如test01、test06等）

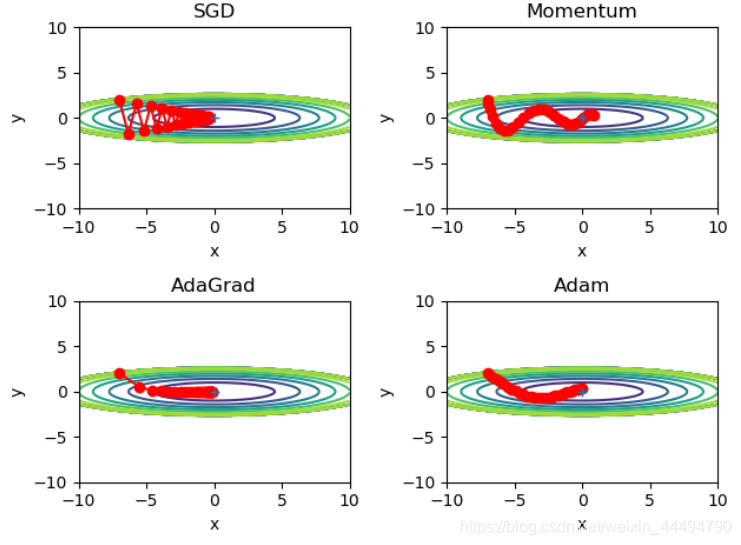
二、优化方法

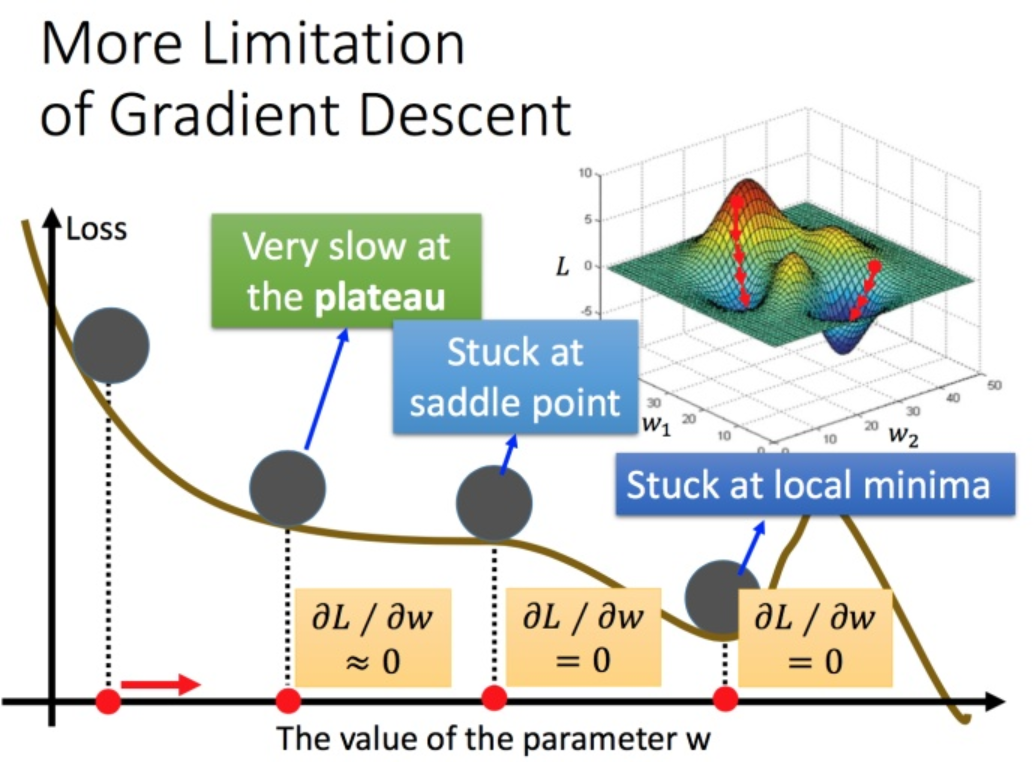
传统的梯度下降优化算法中，可能会碰到以下情况：
碰到平缓区域，梯度值较小，参数优化变慢；碰到鞍点（梯度为0，参数无法优化）；碰到局部最小值。针对这些问题，出现了 Momentum、AdaGrad、RMSprop、Adam 等优化方法

2.1 指数加权平均

我们最常见的算数平均是将所有数相加后除以数量，每个数权重相同；加权平均给每个数赋予不同权重；移动平均计算最近 N 个数的平均。
指数移动加权平均则是：参考各数值，距离越近的数权重越大，距离越远的数权重越小（比如“明天气温”更依赖“昨天气温”，而非“一个月前的气温”）
计算公式
$St={Y1,t=0β⋅St−1+(1−β)⋅Yt,t>0S_t = \begin{cases} Y_1, & t = 0 \\ \beta \cdot S_{t-1} + (1-\beta) \cdot Y_t, & t > 0 \end{cases}$
$S_t$ ：指数加权平均值；
$Y_t$ ： $t$ 时刻的原始值；
$β\beta$ ：调节权重系数（ $β\beta$ 越大，平均数越平缓，历史值影响越强）

我们通过代码模拟 30天气温数据 的指数加权平均：

import torch
import matplotlib.pyplot as pltELEMENT_NUMBER = 30

1. 实际温度

def test01():# 固定随机数种子（保证结果可复现）torch.manual_seed(0)  # 生成30天的随机温度（均值0，标准差10）temperature = torch.randn(size=[ELEMENT_NUMBER, ]) * 10  print(temperature)  # 绘制温度变化days = torch.arange(1, ELEMENT_NUMBER + 1, 1)  # 天数：1~30plt.plot(days, temperature, color='r')         # 折线图plt.scatter(days, temperature)                 # 散点图plt.show()
if __name__ == '__main__':test01()       # 绘制原始温度

运行结果

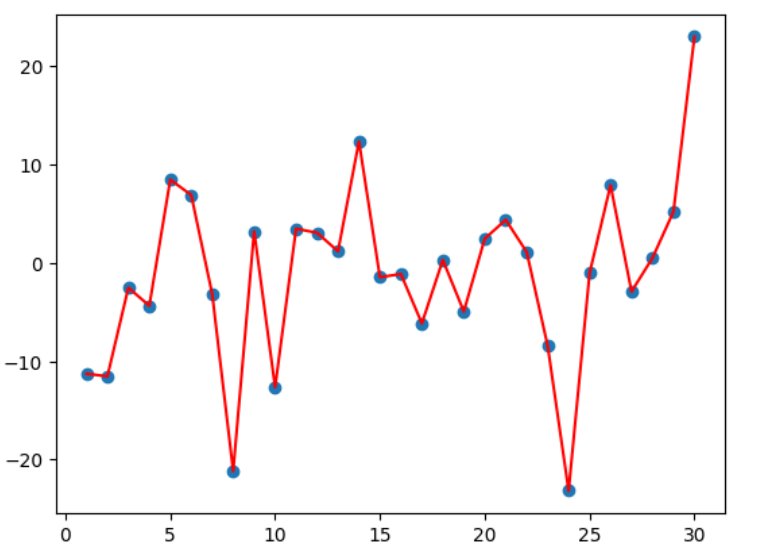
2. 指数加权平均温度（对比不同 $β\beta$ ）

def test02(beta=0.9):# 固定随机数种子torch.manual_seed(0)  # 生成30天的随机温度temperature = torch.randn(size=[ELEMENT_NUMBER, ]) * 10  print(temperature)  exp_weight_avg = []  # 存储指数加权平均结果for idx, temp in enumerate(temperature, 1):  # idx从1开始if idx == 1:# 第1天：加权平均就是自身exp_weight_avg.append(temp)  continue  # 第t天（t>1）：加权平均 = 前一天加权平均×β + 当前温度×(1-β)new_temp = exp_weight_avg[idx - 2] * beta + (1 - beta) * temp  exp_weight_avg.append(new_temp)  # 绘制对比图（加权平均折线 + 原始温度散点）days = torch.arange(1, ELEMENT_NUMBER + 1, 1)  plt.plot(days, exp_weight_avg, color='r')      # 加权平均折线plt.scatter(days, temperature)                 # 原始温度散点plt.show()  if __name__ == '__main__':test02(0.5)    # β=0.5，加权平均（近期影响更大）test02(0.9)    # β=0.9，加权平均（历史影响更强，曲线更平缓）

运行结果

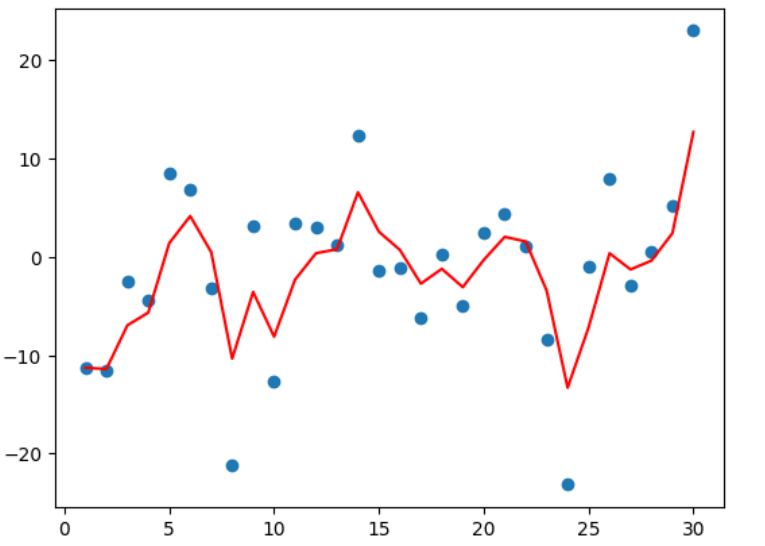
β=0.5 的气温变化（折线）
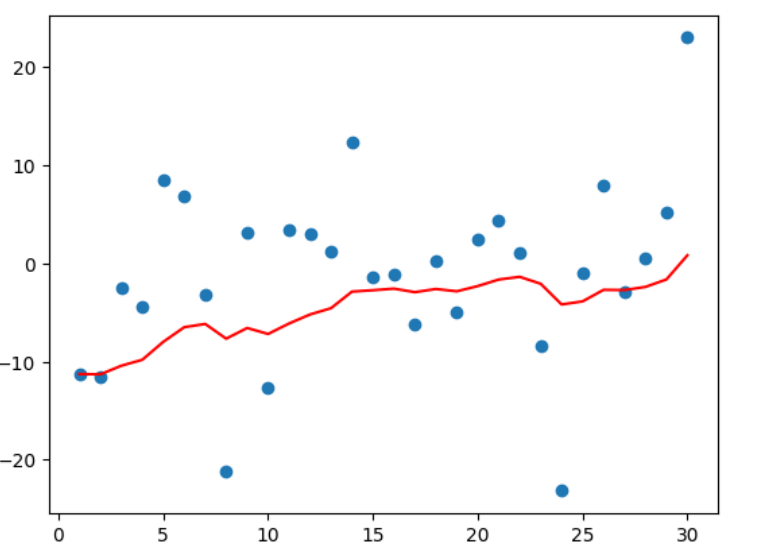
β=0.9 的气温变化（折线）
从程序运行结果可以看到：
指数加权平均绘制出的气温变化曲线更加平缓； $β\beta$ 的值越大，则绘制出的折线越加平缓； $β\beta$ 值一般默认都是 0.9

2.2 Momentum

当梯度下降碰到 “峡谷”、“平缓”、“鞍点” 区域时，参数更新速度变慢。Momentum 通过 指数加权平均法，累积历史梯度值，进行参数更新，越近的梯度值对当前参数更新的重要性越大

📌 梯度计算公式
$Dt=β⋅St−1+(1−β)⋅DtD_t = \beta \cdot S_{t-1} + (1-\beta) \cdot D_t$

$S_{t-1}$ ：历史梯度移动加权平均值；
$D_t$ ：当前时刻的梯度值；
$β\beta$ ：权重系数

📌 梯度下降公式修正

梯度下降公式中梯度的计算，不再是当前时刻 $t$ 的梯度值，而是历史梯度值的指数移动加权平均值。公式修改为：
$Wt+1=Wt−α⋅DtW_{t+1} = W_t - \alpha \cdot D_t$

📌 Momentum 克服问题的原理
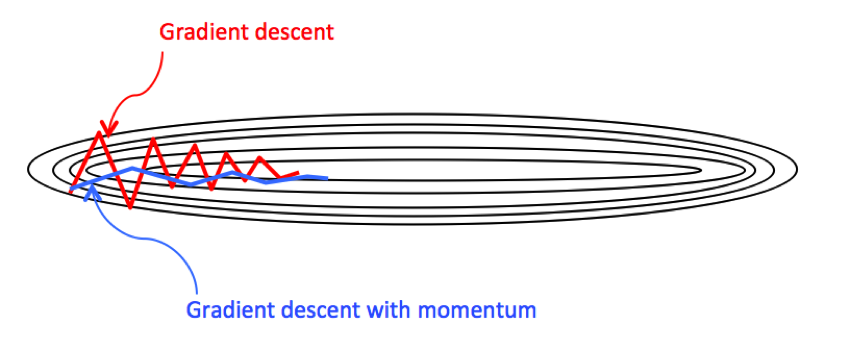
在这里插入图片描述

鞍点：当前梯度为0时，历史累积的梯度可能非零，帮助跨过鞍点；
峡谷/震荡：mini-batch梯度因样本随机导致震荡，Momentum通过加权平均平滑梯度，让更新方向更稳定，加快训练；
注意：Momentum 未优化学习率，仅调整梯度的使用方式

2.3 AdaGrad

AdaGrad 通过对 不同参数分量使用不同的学习率，实现学习率的自适应衰减：
- 初始（离最优解远）：用较大学习率加速训练；
- 迭代后期（接近最优解）：学习率逐渐下降，避免震荡

📌 计算步骤

初始化：学习率 $α\alpha$ 、参数 $θ\theta$ 、小常数 $σ=1e−6\sigma=1e-6$ （防分母为0）；
初始化梯度累积变量 $s = 0$ ；
采样 $m$ 个样本的小批量，计算梯度 $g$ ；
累积平方梯度： $s=s+g⊙g\boldsymbol{s = s + g \odot g}$ （ $⊙\odot$ 表示逐元素相乘）；
学习率更新：
$αnew=αs+σ\alpha_{\text{new}} = \frac{\alpha}{\sqrt{s} + \sigma}$
参数更新：
$θ=θ−αs+σ⋅g\theta = \theta - \frac{\alpha}{\sqrt{s} + \sigma} \cdot g$
重复步骤2~7
- 缺点：学习率 单调递减，可能导致训练后期学习率过小，难以收敛到最优解

2.4 RMSProp

RMSProp 是对 AdaGrad的优化，核心改进：用 指数移动加权平均 替代“历史梯度平方和”，避免学习率下降过快

📌计算步骤

初始化：学习率 $α\alpha$ 、参数 $θ\theta$ 、小常数 $σ=1e−6\sigma=1e-6$ ；
初始化参数 $θ\theta$ ；
初始化梯度累计变量 $s$ ；
采样 $m$ 个样本的小批量，计算梯度 $g$ ；
指数移动加权平均累积梯度：（ $β\beta$ 为权重系数）
$s=β⋅s+(1−β)⋅(g⊙g)\boldsymbol{s = \beta \cdot s + (1-\beta) \cdot (g \odot g)}$
学习率更新（同AdaGrad）：
$αnew=αs+σ\alpha_{\text{new}} = \frac{\alpha}{\sqrt{s} + \sigma}$
参数更新（同AdaGrad）：
$θ=θ−αs+σ⋅g\theta = \theta - \frac{\alpha}{\sqrt{s} + \sigma} \cdot g$

📌 RMSProp 补充说明

RMSProp 与 AdaGrad 最大的区别是 对梯度的累积方式不同，对于每个梯度分量仍然使用不同的学习率
RMSProp 通过引入 衰减系数 $β\beta$ ，控制历史梯度对当前更新的影响程度，在神经网络 非凸优化场景 中表现更优，学习率衰减更合理
与AdaGrad共性：若参数分量的梯度值大 → 对应学习率小；梯度值小 → 对应学习率大（自适应调整）

2.5 Adam

Momentum 用 指数加权平均处理梯度，AdaGrad、RMSProp 用 自适应学习率；Adam 结合两者优点：同时使用 移动加权平均的梯度（类似 Momentum）和 移动加权平均的学习率（类似 RMSProp），实现自适应学习率 + 梯度平滑

2.6 小节

本小节学习的梯度下降优化方法：

Momentum：通过指数加权平均平滑梯度，缓解震荡/鞍点；
AdaGrad：自适应学习率（梯度大→学习率小），但易衰减过快；
RMSProp：优化 AdaGrad 的学习率衰减（用指数加权平均替代累计平方和）；
Adam：融合 Momentum 和 RMSProp，兼顾梯度平滑与自适应学习率，场景适应性强

三、正则化

在训练深层神经网络时，由于模型参数较多，在数据量不足的情况下，很容易过拟合。Dropout 就是在神经网络中一种缓解过拟合的方法。

3.1 Dropout 层的原理和使用

我们知道，缓解过拟合的方式就是降低模型的复杂度，而 Dropout 就是通过减少神经元之间的连接，把稠密的神经网络神经元连接，变成稀疏的神经元连接，从而达到 降低网络复杂度的目的

import torch
import torch.nn as nndef test():# 初始化丢弃层dropout = nn.Dropout(p=0.8)  # 初始化输入数据inputs = torch.randint(0, 10, size=[5, 8]).float()  print(inputs)  print('-' * 50)  outputs = dropout(inputs)  print(outputs)  if __name__ == '__main__':  test()

# 运行结果
tensor([[3., 5., 2., 1., 0., 9., 3., 1.],[1., 0., 3., 6., 6., 7., 9., 6.],[3., 4., 5., 0., 8., 2., 8., 2.],[7., 5., 0., 0., 8., 1., 9., 6.],[1., 0., 2., 9., 4., 3., 9., 3.]])
--------------------------------------------------
tensor([[15.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],[ 0.,  0.,  0.,  0.,  0.,  0., 45., 30.],[ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],[35.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],[ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.]])

我们将 Dropout 层的概率 p 设置为 0.8，此时经过 Dropout 层计算的张量中就出现了很多 0，概率 p 设置值越大，则张量中出现的 0 就越多。上面结果的计算过程如下：
- 先按照 p 设置的概率，随机将部分的张量元素设置为 0；
- 为了校正张量元素被设置为 0 带来的影响，需要对非 0 的元素进行缩放，其缩放因子为：1/(1−p) 。上面代码中 p 的值为 0.8，根据公式缩放因子为：1/(1-0.8) = 5；
- 比如：第 3 个元素，原来是 3，乘以缩放因子之后变成 15
我们也发现了，丢弃概率 p 的值越大，则缩放因子的值就越大，相对其他未被设置的元素就要更多的变大；丢弃概率 p 的值越小，则缩放因子的值就越小，相对应其他未被置为 0 的元素就要有较小的变大

📌当张量某些元素被设置为 0 时，对网络会带来什么影响？

比如上面这种情况，如果输入该样本，会使得某些参数无法更新，请看下面的代码：

import torch
import torch.nn as nn# 设置随机数种子
torch.manual_seed(0)  def calculate_gradient(x, w):  y = x @ w  y = y.sum()  y.backward()  print('Gradient: ', w.grad.reshape(1, -1).squeeze().numpy())  def test01():  # 初始化权重w = torch.randn(15, 1, requires_grad=True)  # 初始化输入数据x = torch.randint(0, 10, size=[5, 15]).float()  # 计算梯度calculate_gradient(x, w)  def test02():  # 初始化权重w = torch.randn(15, 1, requires_grad=True)  # 初始化输入数据x = torch.randint(0, 10, size=[5, 15]).float()  # 初始化丢弃层dropout = nn.Dropout(p=0.8)  x = dropout(x)  # 计算梯度calculate_gradient(x, w)  if __name__ == '__main__':  test01()  print('-' * 70)  test02()

# 程序输出结果:  
Gradient:  [19. 15. 16. 13. 34. 23. 20. 22. 23. 26. 21. 29. 28. 22. 29.]
----------------------------------------------------------------------
Gradient:  [ 5.  0. 35.  0.  0. 45. 40. 40.  0. 20. 25. 45. 55.  0. 10.]

从程序结果来看，是否经过 Dropout 层对梯度的计算产生了不小的影响，例如：经过 Dropout 层之后有一些梯度为 0，这使得参数无法得到更新，从而达到了降低网络复杂度的目的

四、批量归一化

在神经网络的搭建过程中，Batch Normalization（批量归一化） 是经常使用的一个网络层，其主要的作用是 控制数据的分布，加快网络的收敛
我们知道，神经网络的学习其实在学习数据的分布，随着网络的深度增加、网络复杂度增加，一般流经网络的数据都是一个 mini batch，每个 mini batch 之间的数据分布变化非常剧烈，这就使得网络参数频繁的进行大的调整以适应流经网络的不同分布的数据，给模型训练带来非常大的不稳定性，使得模型难以收敛
如果我们对每一个 mini batch 的数据进行标准化之后，数据分布就变得稳定，参数的梯度变化也变得稳定，有助于加快模型的收敛

4.1 批量归一化公式

$\lambda \cdot \frac{x - \text{E}(x)}{\sqrt{\text{Var}(x) + \epsilon}} + \beta$

$λ\boldsymbol{\lambda}$ 和 $β\boldsymbol{\beta}$ 是可学习的参数，相当于对标准化后的值做线性变换（ $λ\lambda$ 为系数， $β\beta$ 为偏置）；
$ϵ\boldsymbol{\epsilon}$ 通常取 1e-5，避免分母为0；
$E(x)\boldsymbol{\text{E}(x)}$ 表示变量的均值；
$Var(x)\boldsymbol{\text{Var}(x)}$ 表示变量的方差。
注意：BN 层不会改变输入数据的维度，只改变输入数据的分布。在实际使用过程中，BN 常常和卷积神经网络结合使用（卷积层的输出结果后接 BN 层）

4.2 BN 层的接口

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)

由于每次使用的是 mini batch 数据集，BN 使用 移动加权平均 近似计算均值和方差，momentum 参数调节移动加权平均值的计算；
affine=False 表示 $λ=1\lambda=1$ 、 $β=0\beta=0$ （不学习线性变换）；反之则学习 $λ\lambda$ 和 $β\beta$ ；
BatchNorm2d 适用于 4D 输入数据，形状为 [N,C,H,W]：
- N：批次大小；
- C：通道数；
- H：高度；
- W：宽度

📌由于每次输入到网络中的是小批量样本，我们用 指数加权平均 近似表示整体样本的均值和方差，更新公式如下：
$running_mean=momentum⋅running_mean+(1.0−momentum)⋅batch_meanrunning_var=momentum⋅running_var+(1.0−momentum)⋅batch_var\small \begin{align*} \text{running\_mean} &= \text{momentum} \cdot \text{running\_mean} + (1.0 - \text{momentum}) \cdot \text{batch\_mean} \\ \text{running\_var} &= \text{momentum} \cdot \text{running\_var} + (1.0 - \text{momentum}) \cdot \text{batch\_var} \end{align*}$

$batch_mean\boldsymbol{\text{batch\_mean}}$ 、 $batch_var\boldsymbol{\text{batch\_var}}$ ：当前批次的均值、方差；
$running_mean\boldsymbol{\text{running\_mean}}$ 、 $running_var\boldsymbol{\text{running\_var}}$ ：近似的整体均值、方差（评估时用其归一化输入）