深度学习模型组件之优化器--动量优化方法（带动量的 SGD 与 Nesterov 加速梯度）

动量优化方法：带动量的 SGD 与 Nesterov 加速梯度

在深度学习模型的训练过程中，选择合适的优化算法对于模型的收敛速度和性能至关重要。 动量优化方法在传统优化算法的基础上，通过引入动量项， 加速收敛并 减小震荡。本文将介绍两种常用的动量优化方法： 带动量的随机梯度下降（SGD with Momentum）和Nesterov 加速梯度（Nesterov Accelerated Gradient, NAG），并将它们与基础优化方法进行对比。

1. 带动量的随机梯度下降（SGD with Momentum）

1.1 基本原理

带动量的 SGD在每次参数更新时，累积之前梯度的指数加权平均，这相当于在梯度下降过程中加入了一个“惯性”，使得优化过程更加平滑。具体更新公式如下：

首先，计算动量项：

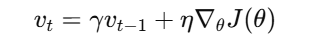
其中：

• vt为当前动量，
• γ为动量因子（通常取值在0到1之间），
• η为学习率，
• ∇θJ(θ)为当前梯度。

然后，更新参数：

1.2 优点与缺点

优点：

• 加速收敛：在梯度方向一致的情况下，动量项的累积效应可以加快收敛速度。
• 减小震荡：在损失函数的狭长谷地中，动量可以有效减小参数更新的震荡。

缺点：

• 参数选择敏感：动量因子的选择需要谨慎，过大可能导致不稳定，过小则效果不明显。

1.3 SGD with Momentum代码示例

import numpy as np

# 假设我们要最小化 f(x) = x^2
def f(x):
    return x ** 2

def grad_f(x):
    return 2 * x

# 初始化参数
x = 10.0
learning_rate = 0.1
momentum = 0.9
num_iterations = 50
v = 0  # 初始化动量

for i in range(num_iterations):
    grad = grad_f(x)
    v = momentum * v + learning_rate * grad
    x = x - v
    print(f"Iteration {i+1}: x = {x}, f(x) = {f(x)}")

2. Nesterov 加速梯度（Nesterov Accelerated Gradient, NAG）

2.1 基本原理

Nesterov 加速梯度是在动量方法的基础上进行改进的一种优化算法。它在计算梯度时，先对参数进行一个动量方向的预估，然后在预估的位置计算梯度，从而提高优化方向的准确性。具体更新公式如下：

• 首先，计算预估位置：

  

• 然后，在预估位置计算梯度并更新动量项：

  

• 最后，更新参数：

  

2.2 优点与缺点

优点：

• 更准确的更新方向：由于在预估位置计算梯度，NAG能够提前感知未来位置的变化趋势，从而进行更有效的更新。
• 加速收敛：相比于传统动量方法，NAG在某些情况下可以实现更快的收敛速度。

缺点：

• 计算复杂度增加：每次迭代需要两次参数更新，计算量略有增加。

2.3 Nesterov Accelerated Gradient代码示例

import numpy as np

# 假设我们要最小化 f(x) = x^2
def f(x):
    return x ** 2

def grad_f(x):
    return 2 * x

# 初始化参数
x = 10.0
learning_rate = 0.1
momentum = 0.9
num_iterations = 50
v = 0  # 初始化动量

for i in range(num_iterations):
    temp_x = x - momentum * v
    grad = grad_f(temp_x)
    v = momentum * v + learning_rate * grad
    x = x - v
    print(f"Iteration {i+1}: x = {x}, f(x) = {f(x)}")

3. 动量优化方法与基础优化方法的对比

下表对比了基础优化方法（梯度下降、随机梯度下降、小批量梯度下降）与动量优化方法（带动量的 SGD、Nesterov 加速梯度）的特点：

优化方法	优点	缺点
梯度下降（GD）	理论简单，更新方向稳定	计算量大，收敛速度慢，易陷入局部最优
随机梯度下降（SGD）	更新速度快，适合大数据集，易跳出局部最优	更新过程有噪声，收敛路径不平滑
小批量梯度下降	兼顾计算效率与稳定性，适合并行计算	批量大小选择敏感，过小噪声大，过大失去随机性
带动量的 SGD	加速收敛，减小震荡	动量因子选择敏感，需谨慎调整
Nesterov 加速梯度	提前预估，更新更准确，加速收敛	计算复杂度增加，每次迭代需两次参数更新

4. 总结

• 带动量的 SGD：通过累积梯度的指数加权平均，引入“惯性”来减少震荡，使优化过程更加平滑，提高收敛速度。适用于高噪声环境下的优化问题。
• Nesterov 加速梯度（NAG）：在带动量的 SGD 基础上，先进行一步“预估”计算，再基于“预估位置”计算梯度，使更新方向更加精准，减少高曲率区域的震荡，提高优化效果。
• 对比分析：
  • 带动量的 SGD 适用于一般优化任务，能有效减少震荡，加快收敛。
  • NAG 在此基础上进一步优化方向，提高优化精度，但计算复杂度略高。
  • 如果希望更快跳出局部最优，NAG 是更优选择；如果计算资源有限，带动量的 SGD 依然是非常有效的方法。