【符号论】群的概念与五行关系的循环群结构

群的定义

给定集合 $G$, 与运算 $\circ$,

• 结合律： $\forall a,b,c\in G$, $(a\circ b)\circ c=a\circ (b\circ c)$,
• 单位元： $\exists e\in G$,$\forall a\in G$, $a\circ e=e\circ a=a$,
• 逆元： $\forall a\in G$, $\exists b\in G$, $a\circ b=b\circ a=e$, 称 $b$ 是 $a$ 的逆元，记为 $b=a^{-1}$
  则称 $(G,\circ )$ 为一个群

循环群

给定群 $(G,\circ )$， 如果存在 $a\in G$, 满足 G={a,a2,a3,⋯ }G=\{a,a^2,a^3,\cdots\}G={a,a2,a3,⋯}，则称 $G$ 是循环群，称 $a$ 是生成元。

$(Z_n,+)$: 剩余类加群是一个循环群. 即 Zn={0,1,⋯ ,n−1}Z_n=\{0,1,\cdots,n-1\}Zn​={0,1,⋯,n−1}, 由于加法的结合律，剩余类加法也满足结合律
即 $((a+b)+c)\mathrm{m}\mathrm{o}\mathrm{d}n=(a+(b+c))\mathrm{m}\mathrm{o}\mathrm{d}n$. $0$ 是单位元 $(0+a)\mathrm{m}\mathrm{o}\mathrm{d}n=(a+0)\mathrm{m}\mathrm{o}\mathrm{d}n=a\mathrm{m}\mathrm{o}\mathrm{d}n$.
逆元为 $n-a$, 因为 $(a+(n-a))\mathrm{m}\mathrm{o}\mathrm{d}n=((n-a)+a)\mathrm{m}\mathrm{o}\mathrm{d}n=n\mathrm{m}\mathrm{o}\mathrm{d}n=0$. 并且 1 就是生成元。

置换群

考虑所有形如 $(1,2,3)$ 的映射关系构成的集合，与映射的复合运算， 称为置换群

例如 S2={(1),(1,2)}S_2=\{(1),(1,2)\}S2​={(1),(1,2)}, 单位元是 $(1)$, (1映射到1，2映射到2）， $(1,2)$ 表示 1映射到2，2映射到1。
因此 $(1)$ 的逆是 $(1)$, $(1,2)$ 的逆还是 $(1,2)$. 即 $S_2$ 也是由 $(1,2)$ 生成的循环群。
例如 S3={(1),(1,2),(2,3),(1,3),(1,2,3),(1,3,2)}S_3=\{(1),(1,2),(2,3),(1,3),(1,2,3), (1,3,2)\}S3​={(1),(1,2),(2,3),(1,3),(1,2,3),(1,3,2)}, 则 单位元还是 $(1)$, 其中 $(1,2)$ 表示 1映射到2，2映射到1， 3映射到3. $(1,2,3)$ 表示 1映射到2，2映射到3，3映射到1. 然而 $S_3$ 不是循环群，例如 $(1,2,3{)}^2=(1,3,2)$, 而 $(1,2,3{)}^3=(1)$， 因此 $(1,2,3)$ 不是生成元，类似的 $(1,2{)}^2=(1)$ 也不是生成元，根据枚举法 $S_3$没有生成元。 但是其子群 A3={(1),(1,2,3),(1,3,2)}A_3=\{(1),(1,2,3),(1,3,2)\}A3​={(1),(1,2,3),(1,3,2)} 一个循环群， 生成元是 $(1,2,3)$。

五行基本元素

五行基本元素包括： 金，水，木，火，土
首先要声明： 五行只是朴素的一种辩证法，不可用于所有现代生活中，因此仍然要遵循现代科学解决生活中遇到的问题（包括物理，化学，生物等领域）。 五行学说通常在命理学，中医学，中药学中扮演着重要角色，用于简化逻辑关系推断的工具。

五行关系

相生关系：

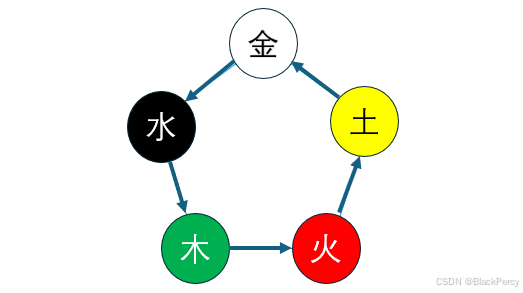
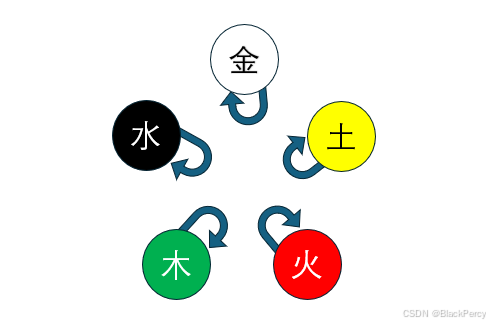
金生水，水生木，木生火，火生土，土生金

朴素解释：

1. 金生水：天冷金属表面会附着水汽（前提是金属在的空气中要有水蒸气，否则不会附着水汽）
2. 水生木：没有水汽，则植物不会发芽
3. 木生火：干燥的木柴可以被点燃（前提是空气中要有氧气参与氧化还原反应）
4. 火生土：可燃物质燃烧后剩下的灰烬被认为是土（包括菌群腐蚀后的食物等也可以视为土）
5. 土生金：从土壤中可以挖出金属或提取金属。

函数形式
${\sigma }_{生}(金)=水$
${\sigma }_{生}(水)=木$
${\sigma }_{生}(木)=火$
${\sigma }_{生}(火)=土$
${\sigma }_{生}(土)=金$

置换群表示
${\sigma }_{生}=(金，水，木，火，土)$

相克关系：

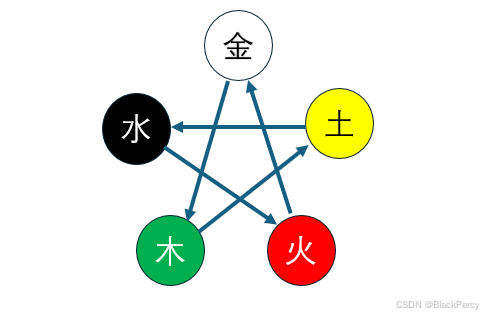
金克木，木克土，土克水，水克火，火克金

朴素解释：

金克木：可以用金属制刀具切割锯断木头
木克土：盆栽发育到一定程度，土壤渐渐被根系吸收成为空盆
土克水：水来土屯 或 水来土堰
水克火：用水扑灭火（但水不能用于镁粉等特殊可燃物的灭火，也不能用于油锅灭火）
火克金：高温可以融化金属变形，也可以煅烧金属变性

函数形式
${\sigma }_{克}(金)=木={\sigma }_{生}^2(金)$
${\sigma }_{克}(水)=火={\sigma }_{生}^2(水)$
${\sigma }_{克}(木)=土={\sigma }_{生}^2(木)$
${\sigma }_{克}(火)=金={\sigma }_{生}^2(火)$
${\sigma }_{克}(土)=水={\sigma }_{生}^2(土)$

置换群表示
${\sigma }_{克}=(金，木，土，水，火)={\sigma }_{生}^2$

相悔关系

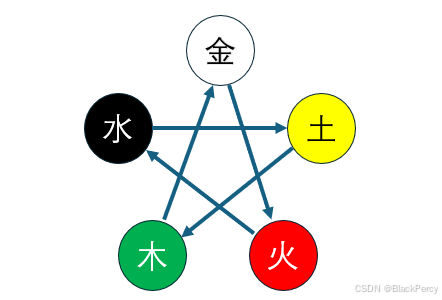
金侮火，火侮水，水侮土，土侮木，木侮金
朴素解释
金侮火：火源不足，则劲也可斩断火源（例如断绝氧气）
火侮水：水不够多，则火将水气化消耗
水侮土：土不足稳固，则被大水漫灌
土侮木：木不足钻劲，则根系无法钻入土壤而生长
木侮金：金不够锋利，则无法斩断木材

函数形式
${\sigma }_{侮}(金)=火={\sigma }_{生}^3(金)$
${\sigma }_{侮}(水)=土={\sigma }_{生}^3(水)$
${\sigma }_{侮}(木)=金={\sigma }_{生}^3(木)$
${\sigma }_{侮}(火)=水={\sigma }_{生}^3(火)$
${\sigma }_{侮}(土)=木={\sigma }_{生}^3(土)$

置换群表示
${\sigma }_{侮}=(金，火，水，土，木)={\sigma }_{生}^3$

相泄关系

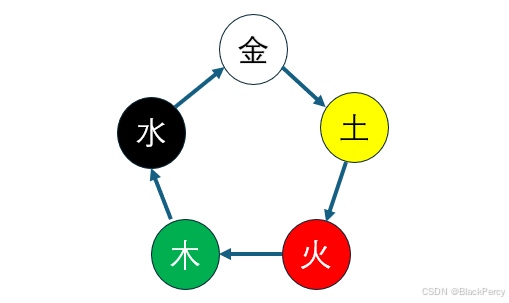
金泄土，土泄火，火泄木，木泄水，水泄金。

朴素解释

1. 水泄金：水（如雨水、河流）的冲刷和腐蚀作用会消耗金属（金）。
2. 金泄土：金属器物（金）从土地（土）中被开采冶炼出来，这个过程消耗了土的能量。
3. 土泄火：灰土（土）覆盖可以熄灭火焰（火），是火生土后，土对火的反向制约。
4. 火泄木：燃烧（火）的过程会耗尽木材（木）的能量。
5. 木泄水：树木（木）的生长会吸收和消耗水分（水）。

函数形式
${\sigma }_{泄}(水)=金={\sigma }_{生}^{-1}(金)$
${\sigma }_{泄}(金)=土={\sigma }_{生}^{-1}(土)$
${\sigma }_{泄}(土)=火={\sigma }_{生}^{-1}(火)$
${\sigma }_{泄}(火)=木={\sigma }_{生}^{-1}(木)$
${\sigma }_{泄}(木)=水={\sigma }_{生}^{-1}(水)$

置换群表示
${\sigma }_{泄}=(水,金,土,火,木)={\sigma }_{生}^4={\sigma }_{生}^{-1}$

相帮关系

金帮金，水帮水，火帮火，木帮木，土帮土。

朴素解释： 物以类聚人以群分。

函数形式
${\sigma }_{帮}(金)=金={\sigma }_{生}^0(金)$
${\sigma }_{帮}(水)=水={\sigma }_{生}^0(水)$
${\sigma }_{帮}(木)=木={\sigma }_{生}^0(木)$
${\sigma }_{帮}(火)=火={\sigma }_{生}^0(火)$
${\sigma }_{帮}(土)=土={\sigma }_{生}^0(土)$

置换群形式
${\sigma }_{帮}=(金)$.

五行关系群

考虑映射 $f:Z^5\to G$
$f:0\to {\sigma }_{帮}={\sigma }_{生}^0={\sigma }_{帮}^{-1}$
$f:1\to {\sigma }_{生}={\sigma }_{生}^1={\sigma }_{泄}^{-1}$
$f:2\to {\sigma }_{克}={\sigma }_{生}^2={\sigma }_{侮}^{-1}$
$f:3\to {\sigma }_{侮}={\sigma }_{生}^3={\sigma }_{克}^{-1}$
$f:4\to {\sigma }_{泄}={\sigma }_{生}^4={\sigma }_{生}^{-1}$
因此五行关系群也可以看成是由 ${\sigma }_{生}$ 生成的群, 满足结合律，有单位元 ${\sigma }_{帮}$， 且每个元素都有逆元。

中医理论中的脏器与五行元素对应关系

五行符号	五脏	五腑
金	肺	大肠
水	肾	膀胱
木	肝	胆
火	心脏	小肠
土	脾	胃