【王树森深度强化学习】基本概念 Deep Reinforcement Learning (1/5)

随机变量

• 随机变量：随机变量是一个未知变量，它的值取决于一个随机事件的结果
• 比如抛硬币是一个随机事件，抛硬币的结果就记为 X。它可能有两种取值：0 和 1。在抛硬币之前我是不知道 X 是什么的，但是我知道这个随机时间的概率
  
• 通常用小写字母 x 来表示对随机变量的观测值
  

概率密度函数（Probability Density Function,PDF)

• 它意味着随机变量在某个确定的取值点附近的可能性
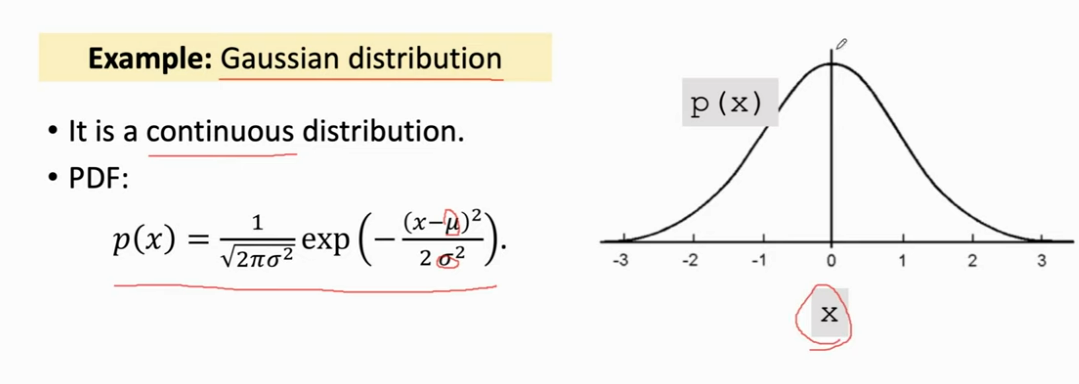
• 高斯分布（也即标准正态分布）是一个连续的概率分布，随机变量 x 的取值可以是任何一个实数
• 下面坐标图的横轴是 x 的取值，纵轴就是概率密度，整体就是高斯分布的概率密度函数。这个概率密度说明这个概率在原点附近的取值概率比较大，在远离原点附近的取值概率比较小
  
• 下面是离散的概率分布，X 只能取 1，3，7
  
• 随机变量 X 的定义域记作 $\mathcal{X}$
• 对于连续的概率密度函数，对定义域算定积分等于1。而离散则是所有取值加起来等于1
  

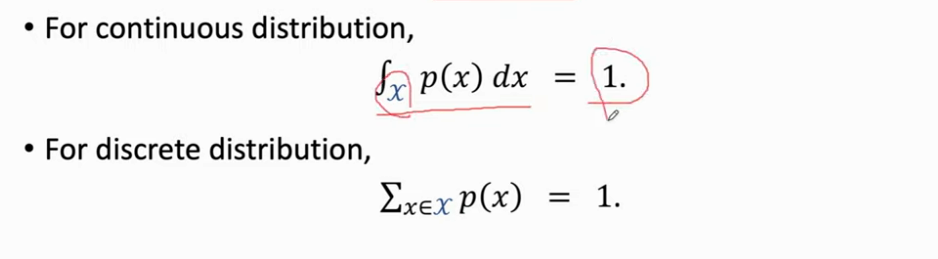
期望（Expectation）

• 对于连续和离散， $f(X)$ 的期望被分别定义为如下
  

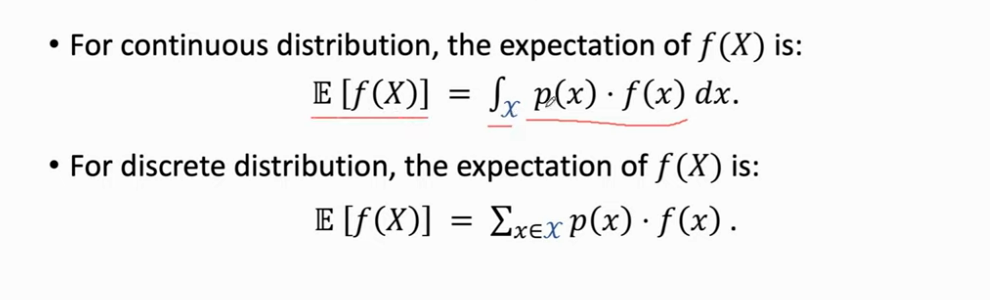
随机抽样（Random Sampling）

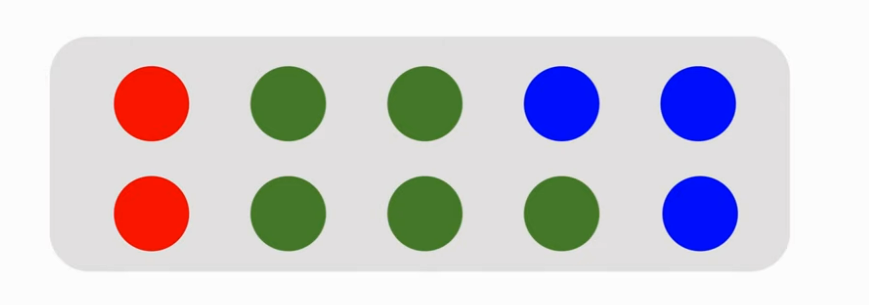
• 有 10 个球：2 个红色，5 个绿色和 3 个蓝色
• 闭着眼睛摸一个球，在我摸到前，我摸到的颜色就是一个随机变量 X，X 有三种可能的取值：红色，绿色和蓝色。现在我真的摸出了一个球，此时我睁开眼睛一看，它便有了观测值：红色。而这个过程就叫随机抽样：我从箱子里面随机抽一个球，并且观测到了抽出来的颜色
  
• 换一种问法：箱子里面有很多个球，我也不知道有多少个。现在做随机抽样，抽到红色球的概率是 0.2，抽到绿色球的概率是 0.5，抽到蓝色球的概率是 0.3。现在依旧摸球，问题和刚刚是一样的
• 那么现在我进行这个过程 100 次，此时便有一定的统计意义了。那么它的红蓝绿的次数应该分别差不多在 20，30，50
• 如果你对随机抽样不熟，你就想想这个摸彩球的例子
  

专业术语（Terminologies）

• 状态（state）$s$：假如在玩超级玛丽，可以理解为状态就是屏幕上的这个画面，这个说法不太严谨，即观测和状态不一定是一样的东西，但是在这节课里可以先这样理解
  
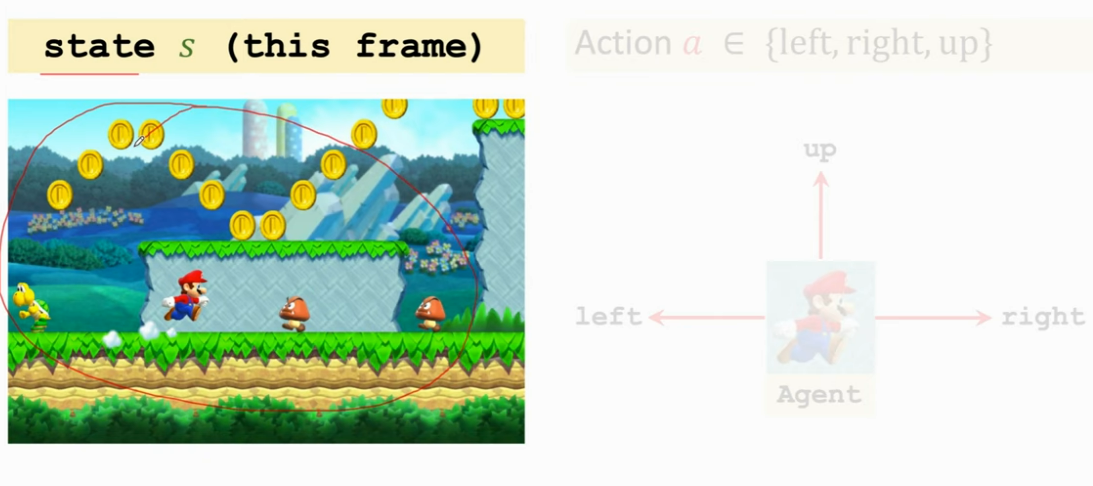
• 马里奥做的动作就叫 Action $a$
• 在这里马里奥被叫做 agent，如果你做的是自驾，那么汽车就是 agent，总之在一个动作里面，动作是由谁做的，谁就是 agent
  
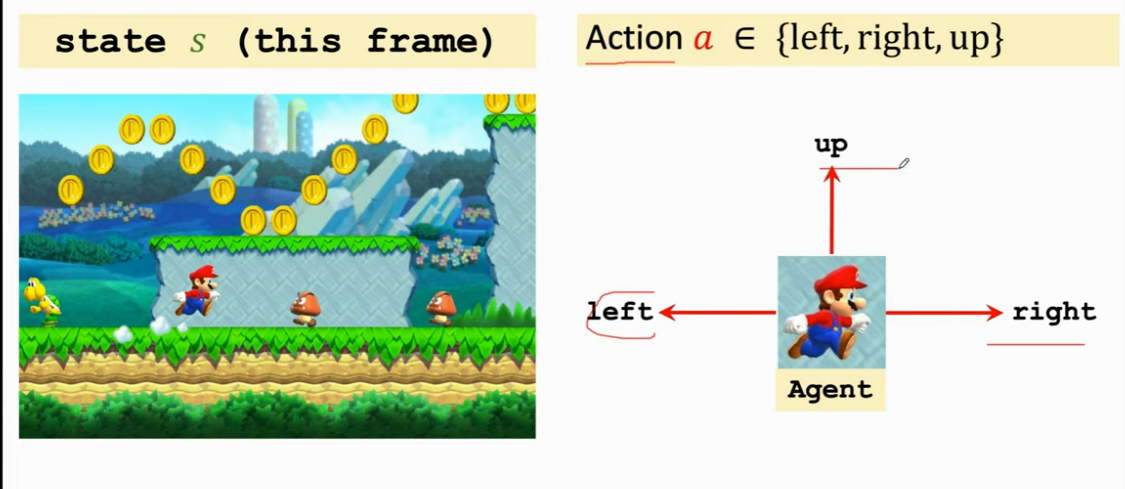
• policy $\pi$：根据观测到的状态而做出决策而控制 agent 运动
• 在这里的 policy 函数是一个概率密度函数，即观测到状态 $s$ 的情况下做出动作 $a$ 的概率
• 强化学习就是去学 policy 函数，只要学好了这个函数，就能自动操纵马里奥赢游戏了
• 这里的 policy 是不确定的 ，也可以去训练确定的 policy
• 在这个游戏训练确定和或者不确定的都行，但是如果要跟人博弈最好还是学不确定的。要是你的动作很固定就很容易被看穿
• reward $R$：agent 做出一个动作，游戏就会给出奖励。这个奖励通常需要我们自己来定义，奖励定义的好坏非常影响强化学习的结果
• 奖励定义举例：
  • 吃金币：$R=+1$
  • 赢游戏：$R=+10000$，赢游戏的奖励应该尽量大，不然马里奥就只会吃金币而不赢游戏
  • 碰到敌人：$R=-10000$，如果碰到敌人就死了
  • 什么也发生：$R=0$
  • 强化学习的目标是获得的奖励总和尽量要高

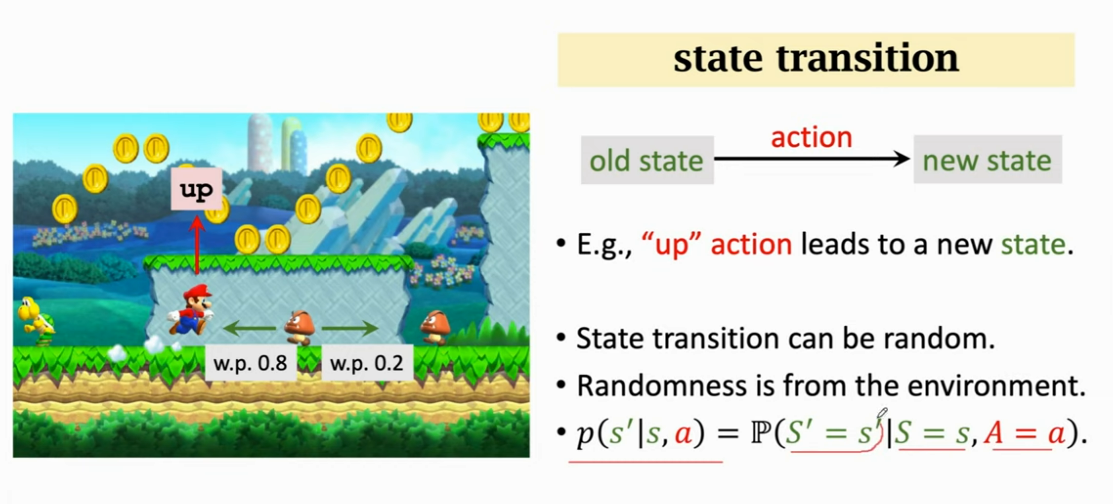
• 状态转移（state transition）：当前状态下马里奥做出一个动作，游戏就会转移为一个新的状态。比如跳一下屏幕画面就不一样了，这就是一个新的状态

• 状态转移可以是确定的也可以是随机的，通常认为是随机的

• 状态转移的随机性是从环境里来的，在这里环境就是游戏的程序，游戏的程序决定下一个状态是什么。比如如果马里奥向上跳这个是确定的，但是敌人左右移动是随机的，由游戏程序决定的，这就造成了下一个状态的随机性

• 可以把状态转移用 $p(s^{\prime }|s,a)$ 函数来表示，它是一个条件概率密度函数，意思是如果观测到当前的状态的 $s$ 以及动作 $a$，$p$ 函数输出 $s^{\prime }$ 的概率

• 在图中这个例子马里奥会跳到上面，而敌人的往左和往右并不确定，分别有一定的概率，这个我们玩家是不可知的，这个状态转移函数只有环境可以知道
  

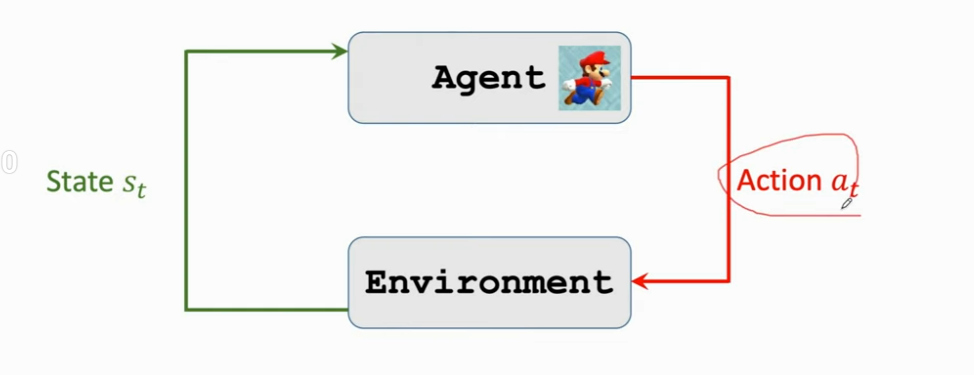
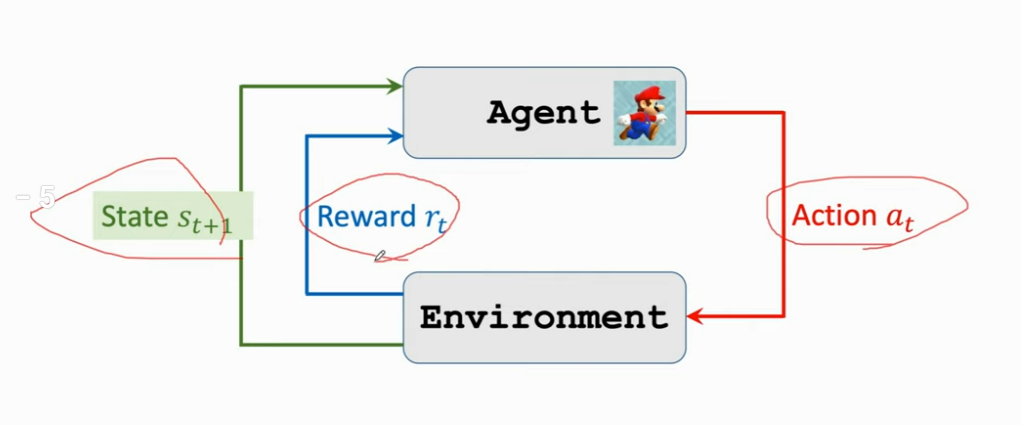
• agent 与环境交互（agent environment interaction）：这里的环境是游戏程序，agent是马里奥，状态 $s_t$ 是环境告诉我们的，这里我们可以把屏幕上显示给我们的游戏画面看作 $s_t$

• 动作 $a_t$ 可以是向左走，向右走或者向上跳
  

• agent 做出动作后，环境会更新状态，更新成 $s_{t+1}$，同时环境会给 agent 一个奖励 $r_t$
  

强化学习中的随机性（Randomness in Reinforcement Learning）

• 强化学习有两个随机性来源，第一个随机性是从 agent 动作中来的，因为动作是根据 policy 函数随机抽样得到的，我们用 policy 函数来控制 agent
• 给定当前观测的状态 $s$，agent 动作 $a$ 是 policy 函数输出的概率来随机抽样。比如说当前观测到状态 $s$，policy 函数会告诉我们每个动作的概率有多大，比如左为 0.2，右为 0.1，上为 0.7
  
• 另一个随机性来源是状态转移，假定 agent 做出了向上跳的动作，环境要生成下一个状态 $S^{\prime }$ ，这个状态 $S^{\prime }$ 具有随机性，环境用状态转移函数 $p$ 算出概率，然后用概率来抽样得到下一个状态 $S^{\prime }$
• 比如图中根据状态转移函数的计算，转移到左边的状态的概率是 0.8，转移到右边的状态的概率是 0.2，这两个都有可能成为下一个状态，系统会做随机抽样来决定下一个状态
  

Play the game using AI

• 我们用强化学习学出来 policy 函数 $\pi$，AI 就是用 policy 函数来控制 agent
• 观测到当前游戏帧状态 $s_1$
• → 用 policy 函数来算一个概率，然后抽样得到动作 $a_1$
• → 环境会生成下一个状态 $s_2$ 和给 agent 奖励 $r_1$
• → 用 policy 函数来算一个概率，然后抽样得到动作 $a_2$
• → ···
• 这样我们就可以得到游戏的轨迹，这个轨迹是每一步的状态，动作，奖励，一直到游戏结束
  

奖励和回报（Rewards and Returns）

• 回报：未来的累计奖励
• $U_t=R_t+R_{t+1}+R_{t+2}+R_{t+3}+\cdot \cdot \cdot$
• 问题：奖励 $R_t$ 和 $R_{t+1}$ 同样重要吗？
• 你更喜欢哪个选项？：
  • 立即给你 100 块
  • 一年后再给你 100 块
• 理性的人应该都是选 100 块，明年得到 100 块不如立刻得到 100 块。但是如果选项变成了立即的只能给 80 块，那么大家的选择就有可能不一样了
• 所以未来的奖励比现在的奖励价值要低，比如未来的 100 可能只值现在的 80
• 需要给未来的奖励打一个折扣，比如 8 折
  
• 折扣回报：打折扣的未来累计奖励
• $\gamma$：折扣率（可调整的超参数），折扣率的设置对强化学习的结果有一定影响
• $U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{R}_{t+3}+\cdot \cdot \cdot$
  
• $U_t$ 是随机的，它有两个随机性来源：动作和新状态的随机性，如上面所述，而对于 $t$ 之后的奖励，它会依赖于当前的状态和动作
• 比如马里奥向上跳吃到了金币，就得到了一个正的奖励。马里奥向右走碰到了一个敌人，就会得到一个很大的副奖励
• 所以给定 $s_t$，那么 $U_t$ 就取决于：$A_t,A_{t+1},A_{t+2},\cdot \cdot \cdot$
  和 $S_{t+1},S_{t+2},\cdot \cdot \cdot$

价值函数（Value Functions）

• $U_t$ 是一个随机变量，在 $t$ 时刻并不知道 $U_t$ 是什么。比如抛硬币，你在 $t$ 时刻还没把它抛出去，所以你也并不知道会得到 1 还是 0
• 如上 $U_t$ 依赖于后面的动作和状态
• 在 $t$ 时刻我并不知道 $U_t$是什么，那我怎么评估当前的形势？此时就可以用到期望，把里面的随机性都用积分给积掉，得到一个实数。比如虽然抛硬币前不知道会得到什么，但是知道正反都是0.5，那么正面的期望（或反面）的就是0.5。同理对随机变量 $U_t$ 求期望得到一个数记作 $Q_{\pi }$
• 把 $U_t$ 当作未来所有状态和所有动作的一个函数，未来的动作和状态都有随机性，动作的概率密度函数是 policy 函数 $\pi$，状态 s 的概率函数是状态转移函数 $p$，期望就是对未来的动作和状态求的。那么除了 $s_t$ 和 $a_t$，其余随机变量都被积掉了。
• 被积掉的随机变量是 $A_{t+1},A_{t+2},\cdot \cdot \cdot$ 以及 $S_{t+1},S_{t+2}$ 等
• 求期望得到的函数 $Q_{\pi }$ 被称为动作价值函数，它只和 $s_t$ 和 $a_t$ 有关，因为未来的都被积掉了。而 $s_t$ 和 $a_t$ 被作为观测到的数值来对待而不是随机变量，$Q_{\pi }$ 的值依赖于 $s_t$ 和 $a_t$，$Q_{\pi }$ 还与 policy 函数 $\pi$ 有关，因为积分的时候会用到 policy 函数，如果 policy 函数不一样，得到的 $Q_{\pi }$ 就会不一样
• 动作价值函数的直观意义：如果用 policy 函数 $\pi$ ，那么在$s_t$ 下做 $a_t$是好还是坏， $Q_{\pi }$ 就会给当前的所有动作打分，是好还是坏
  
• $Q_{\pi }$ 中去掉 $\pi$ 的方法：对所有的 $\pi$ 求一个最大值，我们有无数种 policy 函数，但是我们要用最好的那个 policy 函数，即让 $Q_{\pi }$ 最大的 policy 函数，它叫做最优动作价值函数（Optimal action-value function）
• 它的意义是对动作 $a_t$ 做评价，agent 可以直接根据 $Q^{\ast }$ 来对动作做决策
  
• 状态价值函数（State-value function），这里它和 $Q_{\pi }$，状态，动作都有关，这里可以以 $A$ 为变量，然后求期望把 $A$ 削掉，求期望得到的 $V_{\pi }$ 只和 $\pi$ 和 $s_t$ 有
• 意义：$V_{\pi }$ 可以告诉我们当前的局势好不好，假如根据 policy 函数来下围棋，$V_{\pi }$ 可以告诉我当前的是不是快赢了或者快输了或者不分高下
  
• $Q_{\pi }$ 可以给动作打分，评估这个动作好不好，当状态为 $s$ 时
• $V_{\pi }$ 和动作 A 无关，如果使用 policy $\pi$ ，那么 $V_{\pi }$ 可以评估当前状态 $s$ 好不好
• $E_S[V_{\pi }(S)]$ 可以评估 policy $\pi$ 好不好
  

How does AI control the agent

• 假如我们玩超级玛丽，我们的目标是多吃金币并赢得游戏
• 一种办法是学习一个 policy 函数 $\pi (a|s)$，这个叫 policy based learning，后面会讲。假如我们有一个 $\pi$，我们就可以用它控制 agent 做动作
• 每观测到一个状态 $s_t$，就把 $s_t$ 作为 $\pi$ 的输入，$\pi$ 函数会输出每个动作的概率，随机抽样得到动作 $a_t$，agent 会执行这个动作 $a_t$
  
• 另一种办法是学习最优动作价值函数 $Q^{\ast }(s,a)$，这个在强化学习里面叫 value based learning，价值学习，下节课讲
• 假如我们有了 $Q^{\ast }$，agent 就可以根据 $Q^{\ast }$ 函数来做动作了，$Q^{\ast }$ 可以告诉我们如果处在状态 $s_t$，那么做动作 $a$ 是好还是坏。我们可以知道所有动作下的 Q 值大不大，假如向上跳的 Q 值最大，agent 就应该向上跳。Q 值是对未来奖励总和的期望，如果向上跳的 Q 值最大，那么说明向上跳更容易在未来得到更多的奖励
• 用数学公式可以表示如下

• 以上两种方法学到其中之一就可以了，后面的课程会围绕这两种来进行学习

OpenAI Gym

• 如果你学习到了一个 $\pi$ 函数或者 $Q^{\ast }$ 函数，你就可以把算法用在控制问题上或者小游戏上
• OpenAI Gym 是强化学习最常用的标准库，Gym 有几大类控制问题，第一种是经典控制问题，比如 Cart Pole 和 Pendulum
  
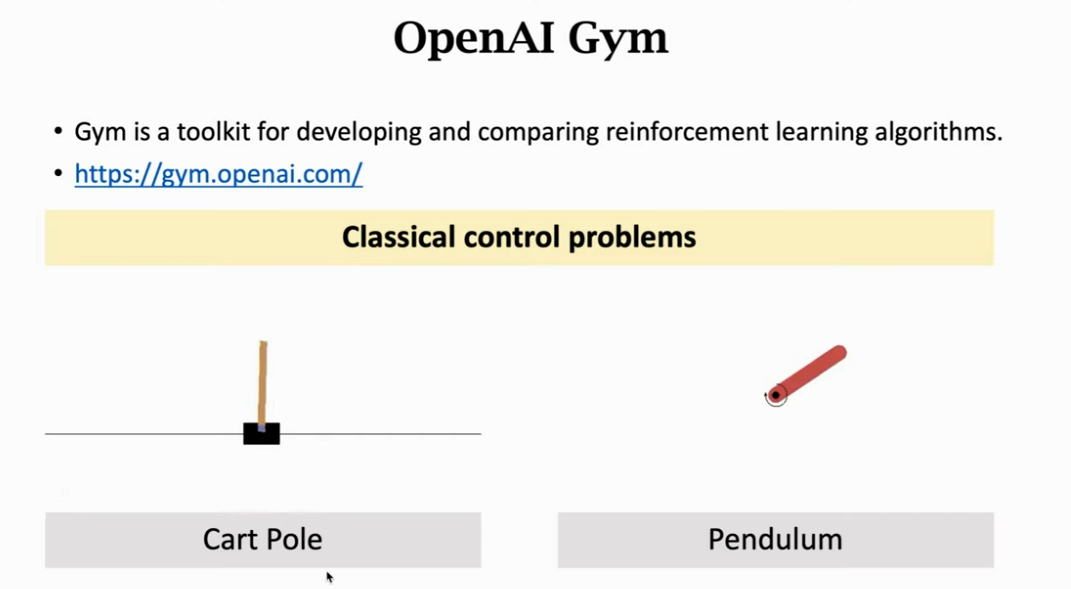
• 第二种是 Atari Game，在小霸王游戏机上的游戏
  
• 第三种是连续控制问题
  
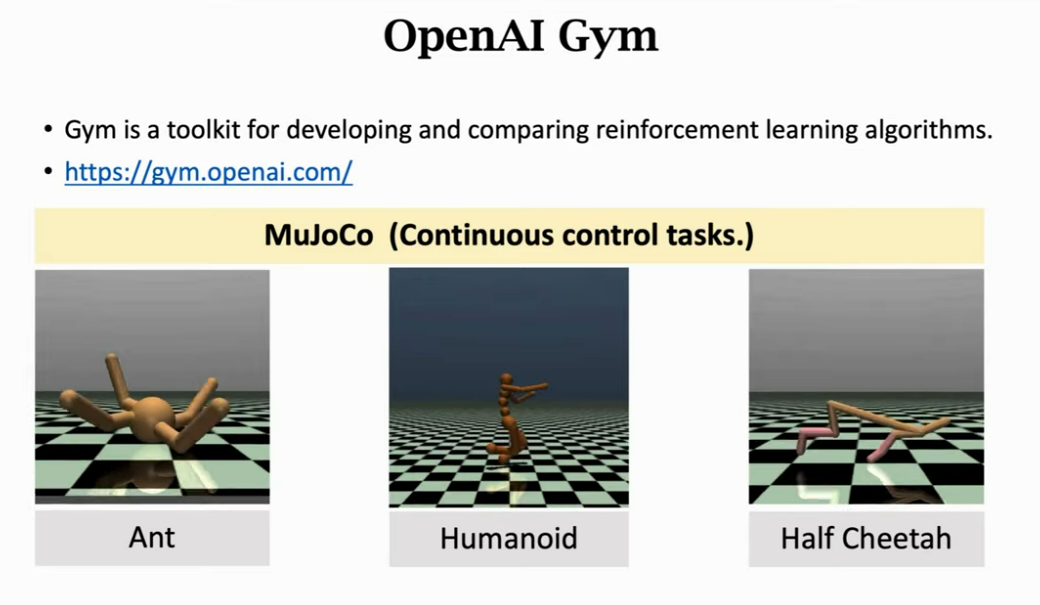
• 所有强化学习学者都会用 Gym 来检验算法
• 用 Gym 做实验很容易，装好之后就可以调用了
  
  

Summary

术语

• Agent：动作的主体，比如超级玛丽中的马里奥
• Environment：agent 可以和环境交互，超级玛丽中的环境就是游戏本身
• State $s$：在超级玛丽中你可以理解为当前显示的画面，游戏玩家会根据画面进行操作
• Action $a$：agent 做出动作后，环境就会更新状态 $s$，并且给出一个奖励 $r$
• Reward $r$：
• 如果状态，动作，奖励等被观测到就用小写字母表示，如果没有被观测到就是一个随机变量，用大写字母表示
• Policy $\pi (a|s)$：观测到状态 $s$，Policy 会输出每个动作的概率
• State transition $p(s^{\prime }|s,a)$：我们是不知道的，环境通过 $p(s^{\prime }|s,a)$ 来随机选择下一个状态

Return and Value

• 回报 Return：把未来所有的奖励都进行加权求和，我们希望 $U_t$ 越大越好，$U_t$ 是一个随机变量，随机性来自于未来所有状态和动作，由于 $U_t$ 的随机性我们在 t 时刻并不知道 $U_t$ 是什么，只有当 agent 玩完游戏才能被观测到，想要在当前就对 Return 就有一个预估的话，可以对其求期望，把其中的随机变量都消掉
  • $U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{R}_{t+3}+\cdot \cdot \cdot$
• 动作价值函数 Action-value function：就是对 $U_t$ 的期望，除了当前状态 $s_t$ 和 $a_t$，其余随机变量被期望消除了，它只和 $s_t$ 和 $a_t$ 以及 $\pi$ 有关
  • $Q_{\pi }(s_t,a_t)=E[U_t|s_t,a_t]$
  • 如果使用 Policy 函数 $\pi$，那么 $Q_{\pi }$ 可以告诉我们在状态 $s_t$ 的情况下做出 $a_t$ 是好还是坏
• 最优动作价值函数 Optimal action-value function：无论用什么样的 Policy 函数，在状态 $s_t$ 做动作 $a_t$ 的最高回报只能是 $Q^{\ast }$
  
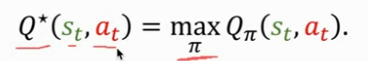
• 状态价值函数 State-value function：再求一次期望，把 $Q_{\pi }$ 中的 $a$ 也给去掉了，$V_{\pi }$ 可以评价状态 $s$ 和 Policy 的好坏。如果给定 Polcy 和状态 $s$，可以告诉我们目前的情况是好是坏，是快赢了还是快输了
  • $V_{\pi }=E_A[Q_{\pi }(s_t,A)]$
    

Play game using reinforcement learning

• 强化学习就是学习怎么控制 agent 基于当前状态做出相应动作，争取能在未来获得相应的奖励
• 流程是观测到状态 $s_t$，agent 会做出动作 $a_t$，然后环境会根据 $s_t$ 和 $a_t$ 来更新状态，给出新的状态 $s_{t+1}$ 和奖励 $r_t$，然后开始下一轮
• 通常是学习 Policy 函数 $\pi (a|s)$ 或者 $Q^{\ast }$，agent 就可以根据这个玩游戏了
• 假如知道 $\pi$，就可以把状态 $s$ 作为输入，输出每个动作的概率，然后做一个随机抽样得到相应的动作 $a$
• 假如知道了 $Q^{\ast }$，就可以用它来评价当前状态下每一个动作的好坏，从而选出 Q 值最高的动作

接下来要学习的内容