深度优先搜索(DFS)
一、前置知识:函数与递归
想要学习深度优先搜索(DFS),首先要知道函数和递归,因为通常深度优先搜索就是使用递归来实现的。
1、什么是函数?
函数就是一个可以复用的代码段,格式如下:
返回类型 函数名(参数1,,...){函数体
}
如下是一个最简单的函数,作用是两数相加:
int add(int a,int b){return a+b;
}
其中,这里的第一个int代表返回类型,表示这个函数返回的值的类型,例如此处如果调用add函数,那么函数运行后就会被一个整型的值“代替”。这个函数的add是函数名,同一个命名空间中不允许出现两个一样的函数名,调用函数时也是根据函数名去寻找对应的代码段。这个函数小括号中的是参数列表,参数列表的类型、数量按需求自定义,调用函数时所传的参数类型、数量要与参数列表中规定的一致,例如调用这个函数就需要传入两个int类型的数据。这个函数大括号中的代码就是函数体,当调用这个函数,就会运行这个函数体中的代码段。函数体中有一个return关键字,当运行到这个关键字时,就会返回这个关键字后面的参数并退出函数返回主代码块,需要注意的是,return后面的代码的类型一定要是定义时返回参数的类型,否则会报错。此外,如果该函数没有返回参数,则返回类型为void,如果这时候还想要使用return强制退出函数,则可以直接使用return ;语句退出。
2、什么是递归?
递归实际上是函数调用了自身,比如:
void a(){a();
}
但是如上图所示的递归并不是有效的递归,因为它没有办法退出,会一直循环,就像写了一个while(true)一样。当真正需要用到递归的时候,需要我们去定义它的退出条件,如下是一个递归实现的gcd函数:
int gcd(int a, int b) {if (b == 0) return a; // 递归出口return gcd(b, a % b); // 递归调用
}根据上述代码可以看出,递归退出的条件其实是当b=0的时候,返回此时a的值,如下图所示:
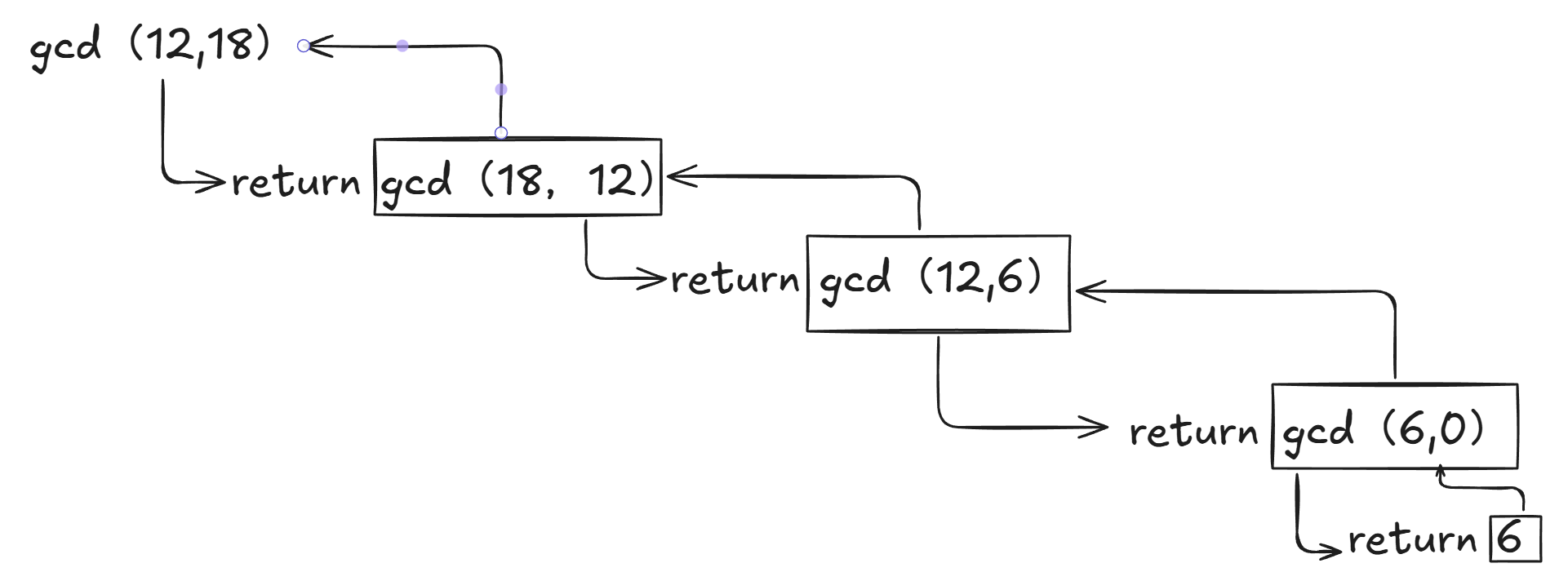
有人说这不就跟循环一样吗?其实所有的循环都可以用递归写,所有的递归也都可以用循环写,今天要讲的DFS,不仅仅可以用递归写,也可以用循环+栈模拟,那么为什么要使用递归来写呢?使用递归来写不需要手动去模拟栈,也更容易理解其中回溯的含义,或许学完DFS之后能对递归的理解更深刻一点。
二、深度优先搜索
1、深度优先搜索的定义
深度优先搜索(DFS)用白话来说就是“一条路走到黑”“不撞南墙不回头”,具体来说就是在搜索过程中, 沿着某一条路径不断向下搜索,直到不能再前进(即到达终点或无未访问的邻接点),再回溯到上一个分叉点,尝试新的路径。
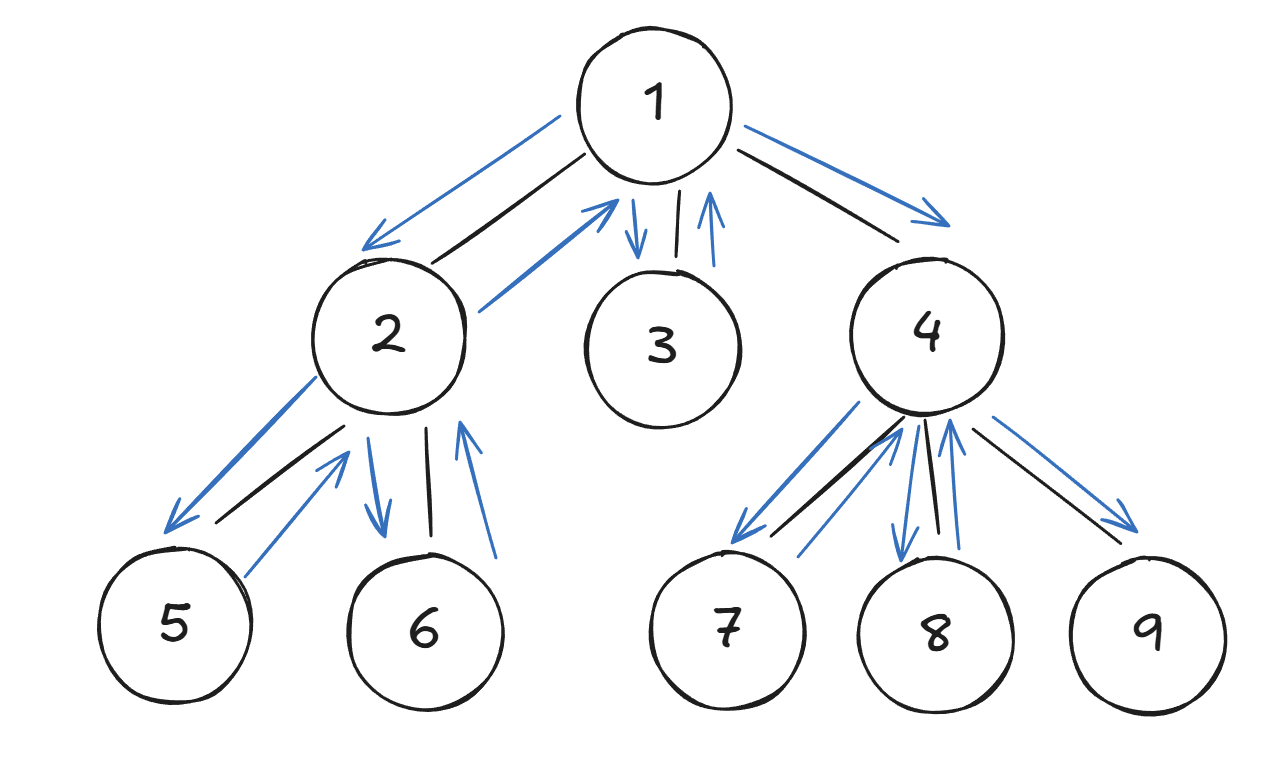
如上图所示,从根节点1开始DFS,先抵达了节点1,虽然它还有3和4两个同级的节点,但是它会沿着这条路径继续走到节点5,此时节点5没有能走的路径了,那就会回溯到节点2,也就是从哪儿来回哪儿去,回退到节点2,重新搜索。
明白了深度优先搜索的搜索方式之后,就到了如何编写代码了。
2、深度优先搜索的编码——以洛谷P1036 选数为例
洛谷P1036 选数
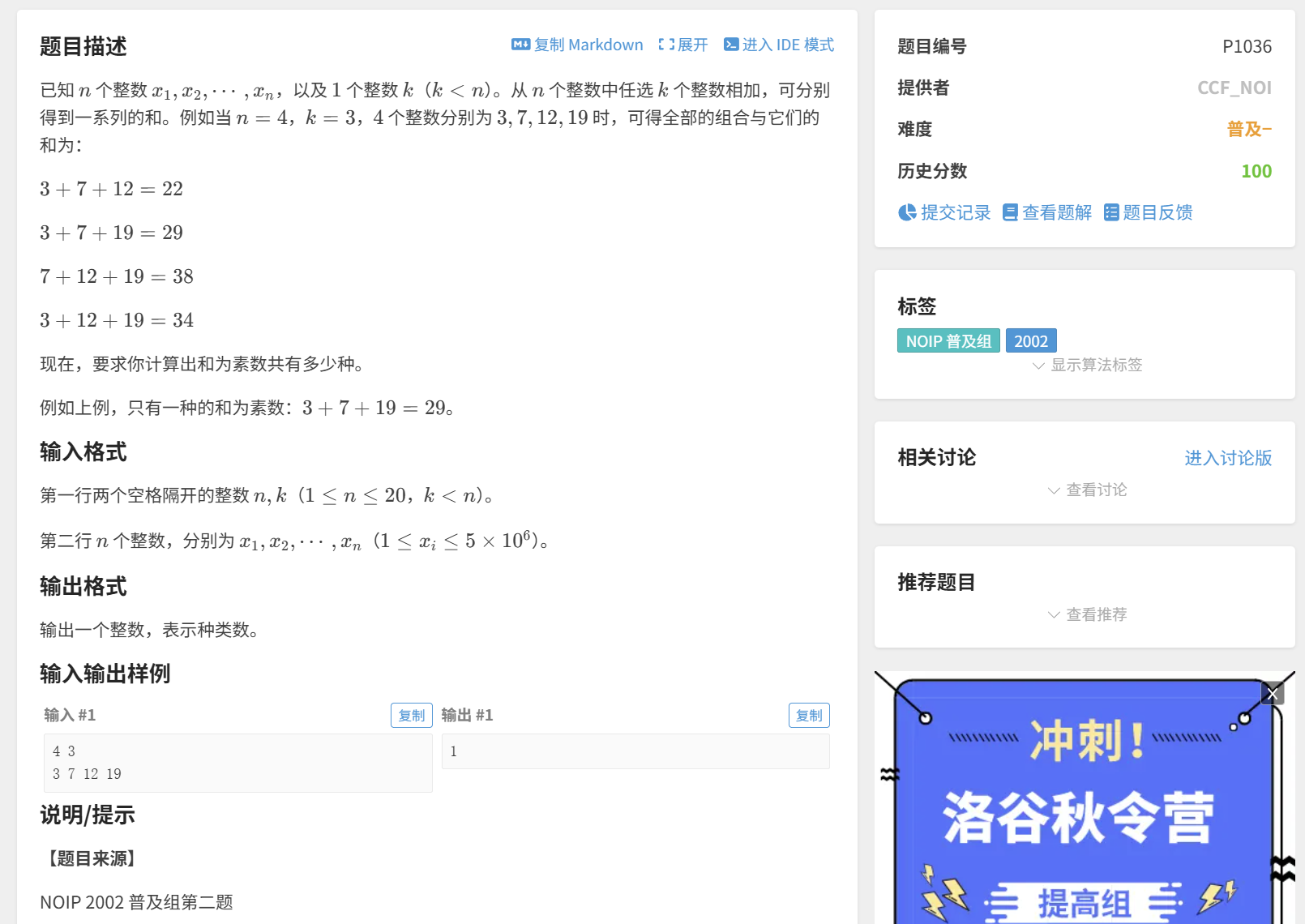
乍一看,大家可能认为这个题跟上面讲的深度优先搜索完全不一样啊,为什么要用深度优先搜索去做?
我们将所有数想象成一个个点,如果要保证选择后不存在相同的排列,那么只要在在选某一个点时,需要选择之前没有被选择的点即可(因为旧的排列也是通过这个方案选出来的,保证了旧的排列是唯一的),那就相当于以每一个数作为头结点做一次深度优先搜索,当深度为k的时候判断当前的总和是否为素数并计数。下图以2为头结点为例,以此类推。
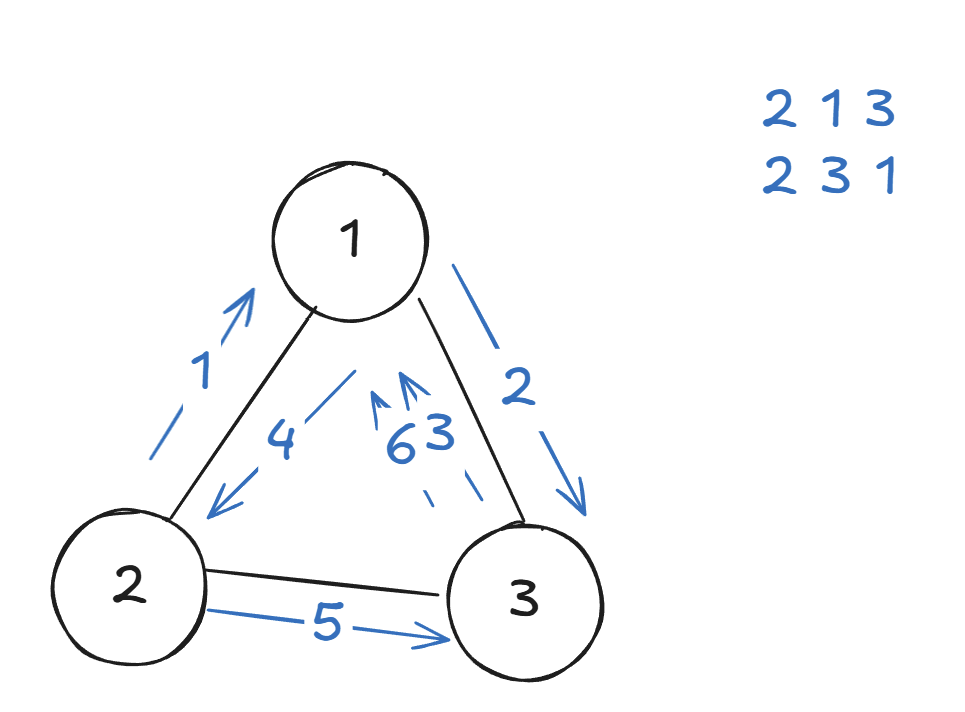
明白了这题为什么要用深度优先搜索之后,我们开始深度优先搜索的编码,核心代码如下:
void dfs(int depth) {if (depth == n) { // 所有数字都被选到一次,输出一个排列for (int i = 0; i < n; ++i) {cout << path[i] << (i == n - 1 ? '\n' : ' ');}return;}for (int i = 0; i < n; ++i) {if (!used[i]) { // 如果这个数还没被选过used[i] = true; // 标记已选path.push_back(a[i]); // 放入当前排列dfs(depth + 1); // 递归进入下一层path.pop_back(); // 回溯:撤销选择used[i] = false;}}
}
完整代码:
#include <bits/stdc++.h>
using namespace std;int n;
int a[25]; // 存放输入的数
bool used[25]; // 标记某个数是否被选过
vector<int> path; // 当前排列void dfs(int depth) {if (depth == n) { // 所有数字都被选到一次,输出一个排列for (int i = 0; i < n; ++i) {cout << path[i] << (i == n - 1 ? '\n' : ' ');}return;}for (int i = 0; i < n; ++i) {if (!used[i]) { // 如果这个数还没被选过used[i] = true; // 标记已选path.push_back(a[i]); // 放入当前排列dfs(depth + 1); // 递归进入下一层path.pop_back(); // 回溯:撤销选择used[i] = false;}}
}int main() {cin >> n;for (int i = 0; i < n; ++i) cin >> a[i];dfs(0);return 0;
}