当前位置：首页 > news >正文

小白python入门 - 12. Python集合——无序容器的艺术与科学

news 2025/11/1 0:32:33

在学习了列表和元组之后，我们再来学习一种容器型的数据类型，它的名字叫集合（set）。说到集合这个词大家一定不会陌生，在数学课本上就有这个概念。如果我们把一定范围的、确定的、可以区别的事物当作一个整体来看待，那么这个整体就是集合，集合中的各个事物称为集合的元素。

一. 集合的本质与特性

Python集合（set）作为无序容器类型的代表，完美继承了数学集合的核心精髓。它不仅是数据结构的实现，更是一种解决特定问题的哲学工具：专注于元素的唯一存在性而非位置关系。

数学三原则的实现:

1. 无序性革命

集合颠覆了序列类型（列表/元组）的索引依赖：

fruits = {"apple", "banana", "cherry"}
# 尝试fruits[0]将引发TypeError（不支持索引）

这种设计迫使开发者摆脱位置思维，聚焦元素本质属性。

2. 互异性保障

自动去重机制是集合核心价值：

unique_chars = set("programming")  
print(unique_chars)  # {'o', 'i', 'p', 'n', 'm', 'a', 'g', 'r'}

输出结果中重复字符（如g/m）被自然过滤，适用于数据清洗场景。

3. 确定性验证

in运算符的哈希加速：

n = 107 
list_data = list(range(n))
set_data = set(range(n))%timeit 9999999 in list_data  # 线性搜索 ≈230ms 
%timeit 9999999 in set_data   # 哈希查找 ≈78ns（快百万倍）

Python 程序中的集合跟数学上的集合没有什么本质区别，需要强调的是上面所说的无序性和互异性。无序性说明集合中的元素并不像列中的元素那样存在某种次序，可以通过索引运算就能访问任意元素，集合并不支持索引运算。另外，集合的互异性决定了集合中不能有重复元素，这一点也是集合区别于列表的地方，我们无法将重复的元素添加到一个集合中。集合类型必然是支持in和not in成员运算的，这样就可以确定一个元素是否属于集合，也就是上面所说的集合的确定性。集合的成员运算在性能上要优于列表的成员运算，这是集合的底层存储特性决定的，此处我们暂时不做讨论，大家记住这个结论即可。

说明：集合底层使用了哈希存储（散列存储），对哈希存储不了解的读者可以先看看“Hello 算法”网站对哈希表的讲解，感谢作者的开源精神。

二. 创建集合的技术实践

在 Python 中，创建集合可以使用{}字面量语法，{}中需要至少有一个元素，因为没有元素的{}并不是空集合而是一个空字典，字典类型我们会在下一节课中为大家介绍。当然，也可以使用 Python 内置函数set来创建一个集合，准确的说set并不是一个函数，而是创建集合对象的构造器，这个知识点会在后面讲解面向对象编程的地方为大家介绍。我们可以使用set函数创建一个空集合，也可以用它将其他序列转换成集合，例如：set('hello')会得到一个包含了4个字符的集合（重复的字符l只会在集合中出现一次）。除了这两种方式，还可以使用生成式语法来创建集合，就像我们之前用生成式语法创建列表那样。

初始化方法对比

方法	语法示例	适用场景
字面量	`{1, 2, 3}`	静态集合初始化
set()构造器	`set([1,2,2,3])`	动态转换可迭代对象
集合推导式	`{x2 for x in range(10)}`	条件筛选转换

哈希性约束深度解析

集合元素必须为不可变类型（hashable），这是哈希表实现的根基：

valid = {1, 3.14, "text", (1,2)}  # 合法 
invalid = { [1,2] }  # TypeError: unhashable type 'list'

哈希冲突处理：当不同对象哈希值相同时（如hash(1)==hash(1.0)），Python使用开放寻址法解决冲突，确保元素唯一性

需要提醒大家，集合中的元素必须是hashable类型，所谓hashable类型指的是能够计算出哈希码的数据类型，通常不可变类型都是hashable类型，如整数（int）、浮点小数（float）、布尔值（bool）、字符串（str）、元组（tuple）等。可变类型都不是hashable类型，因为可变类型无法计算出确定的哈希码，所以它们不能放到集合中。例如：我们不能将列表作为集合中的元素；同理，由于集合本身也是可变类型，所以集合也不能作为集合中的元素。我们可以创建出嵌套列表（列表的元素也是列表），但是我们不能创建出嵌套的集合，这一点在使用集合的时候一定要引起注意。

集合的运算

Python 为集合类型提供了非常丰富的运算，主要包括：成员运算、交集运算、并集运算、差集运算、比较运算（相等性、子集、超集）等。

成员运算

可以通过成员运算in和not in 检查元素是否在集合中，代码如下所示。

set1 = {11, 12, 13, 14, 15}
print(10 in set1)      # False 
print(15 in set1)      # True
set2 = {'Python', 'Java', 'C++', 'Swift'}
print('Ruby' in set2)  # False
print('Java' in set2)  # True

二元运算

集合的二元运算主要指集合的交集、并集、差集、对称差等运算，这些运算可以通过运算符来实现，也可以通过集合类型的方法来实现，代码如下所示。

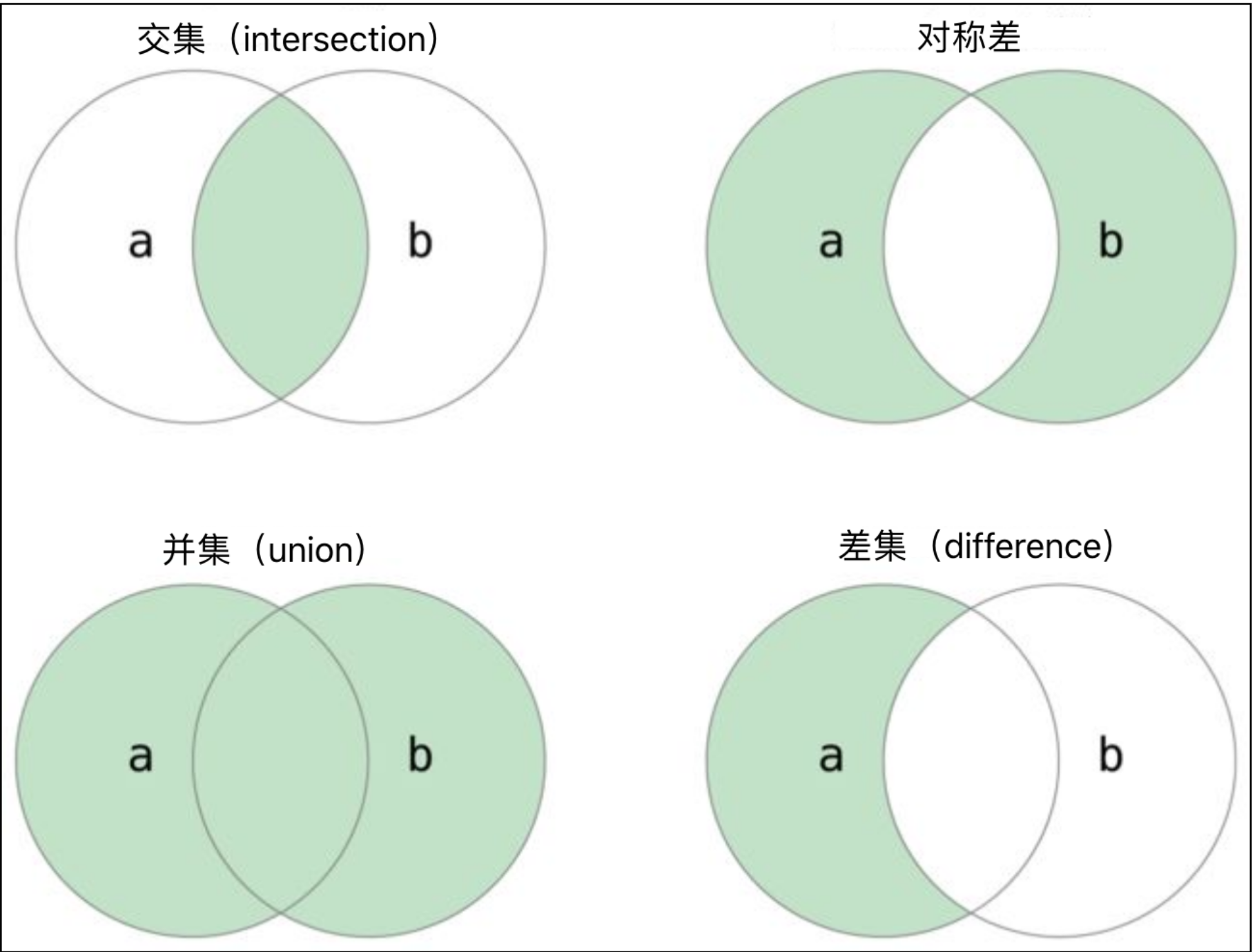
在这里插入图片描述

set1 = {1, 2, 3, 4, 5, 6, 7}
set2 = {2, 4, 6, 8, 10}# 交集
print(set1 & set2)                      # {2, 4, 6}
print(set1.intersection(set2))          # {2, 4, 6}# 并集
print(set1 | set2)                      # {1, 2, 3, 4, 5, 6, 7, 8, 10}
print(set1.union(set2))                 # {1, 2, 3, 4, 5, 6, 7, 8, 10}# 差集
print(set1 - set2)                      # {1, 3, 5, 7}
print(set1.difference(set2))            # {1, 3, 5, 7}# 对称差
print(set1 ^ set2)                      # {1, 3, 5, 7, 8, 10}
print(set1.symmetric_difference(set2))  # {1, 3, 5, 7, 8, 10}

通过上面的代码可以看出，对两个集合求交集，&运算符和intersection方法的作用是完全相同的，使用运算符的方式显然更直观且代码也更简短。需要说明的是，集合的二元运算还可以跟赋值运算一起构成复合赋值运算，例如：set1 |= set2相当于set1 = set1 | set2，跟|=作用相同的方法是update；set1 &= set2相当于set1 = set1 & set2，跟&=作用相同的方法是intersection_update，代码如下所示。

set1 = {1, 3, 5, 7}
set2 = {2, 4, 6}
set1 |= set2
# set1.update(set2)
print(set1)  # {1, 2, 3, 4, 5, 6, 7}
set3 = {3, 6, 9}
set1 &= set3
# set1.intersection_update(set3)
print(set1)  # {3, 6}
set2 -= set1
# set2.difference_update(set1)
print(set2)  # {2, 4}

比较运算

两个集合可以用==和!=进行相等性判断，如果两个集合中的元素完全相同，那么==比较的结果就是True，否则就是False。如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集，即对于 $∀a∈A\small{\forall{a} \in {A}}$ ，均有 $a∈B\small{{a} \in {B}}$ ，则 $A⊆B\small{{A} \subseteq {B}}$ ，A是B的子集，反过来也可以称B是A的超集。如果A是B的子集且A不等于B，那么A就是B的真子集。Python 为集合类型提供了判断子集和超集的运算符，其实就是我们非常熟悉的<、<=、>、>=这些运算符。当然，我们也可以通过集合类型的方法issubset和issuperset来判断集合之间的关系，代码如下所示。

set1 = {1, 3, 5}
set2 = {1, 2, 3, 4, 5}
set3 = {5, 4, 3, 2, 1}print(set1 < set2)   # True
print(set1 <= set2)  # True
print(set2 < set3)   # False
print(set2 <= set3)  # True
print(set2 > set1)   # True
print(set2 == set3)  # Trueprint(set1.issubset(set2))    # True
print(set2.issuperset(set1))  # True

说明：上面的代码中，set1 < set2判断set1是不是set2的真子集，set1 <= set2判断set1是不是set2的子集，set2 > set1判断set2是不是set1的超集。当然，我们也可以通过set1.issubset(set2)判断set1是不是set2的子集；通过set2.issuperset(set1)判断set2是不是set1的超集。

集合的方法

刚才我们说过，Python 中的集合是可变类型，我们可以通过集合的方法向集合添加元素或从集合中删除元素。

set1 = {1, 10, 100}# 添加元素
set1.add(1000)
set1.add(10000)
print(set1)  # {1, 100, 1000, 10, 10000}# 删除元素
set1.discard(10)
if 100 in set1:set1.remove(100)
print(set1)  # {1, 1000, 10000}# 清空元素
set1.clear()
print(set1)  # set()

说明：删除元素的remove方法在元素不存在时会引发KeyError错误，所以上面的代码中我们先通过成员运算判断元素是否在集合中。集合类型还有一个pop方法可以从集合中随机删除一个元素，该方法在删除元素的同时会返回（获得）被删除的元素，而remove和discard方法仅仅是删除元素，不会返回（获得）被删除的元素。

集合类型还有一个名为isdisjoint的方法可以判断两个集合有没有相同的元素，如果没有相同元素，该方法返回True，否则该方法返回False，代码如下所示。

set1 = {'Java', 'Python', 'C++', 'Kotlin'}
set2 = {'Kotlin', 'Swift', 'Java', 'Dart'}
set3 = {'HTML', 'CSS', 'JavaScript'}
print(set1.isdisjoint(set2))  # False
print(set1.isdisjoint(set3))  # True

不可变集合

Python 中还有一种不可变类型的集合，名字叫frozenset。set跟frozenset的区别就如同list跟tuple的区别，frozenset由于是不可变类型，能够计算出哈希码，因此它可以作为set中的元素。除了不能添加和删除元素，frozenset在其他方面跟set是一样的，下面的代码简单的展示了frozenset的用法。

fset1 = frozenset({1, 3, 5, 7})
fset2 = frozenset(range(1, 6))
print(fset1)          # frozenset({1, 3, 5, 7})
print(fset2)          # frozenset({1, 2, 3, 4, 5})
print(fset1 & fset2)  # frozenset({1, 3, 5})
print(fset1 | fset2)  # frozenset({1, 2, 3, 4, 5, 7})
print(fset1 - fset2)  # frozenset({7})
print(fset1 < fset2)  # False

集合运算实战矩阵

运算类型	运算符	方法	数学表示
交集	`&`	`intersection()`	A ∩ B
并集	`	`	`union()`
差集	`-`	`difference()`	A - B
对称差	`^`	`symmetric_difference()`	(A∪B) - (A∩B)

关系数据库替代方案：在处理百万级用户数据时，集合运算比SQL JOIN更高效：

查找使用IOS但未使用Android的用户 
ios_users = set(get_ios_users())
android_users = set(get_android_users())
result = ios_users - android_users

高级方法与模式

元素操作安全策略

active_sessions = {101, 205, 308}安全删除（元素不存在不报错）
active_sessions.discard(999)  带校验删除 
try:active_sessions.remove(999)
except KeyError:logging.warning("尝试删除不存在的会话ID")随机弹出（适用于任务调度）
while active_sessions:task = active_sessions.pop()process_task(task)

集合关系判定

required_skills = {"Python", "SQL", "Git"}
candidateA = {"Python", "Java", "Docker"}print(required_skills.isdisjoint(candidateA))  # False（有交集）
print(candidateA.issubset(required_skills))    # False 
print(required_skills <= candidateA)           # 子集检查

不可变集合(frozenset)的妙用

frozenset突破集合不能嵌套的限制：

创建嵌套集合
graph_nodes = {frozenset({"A", "B"}): 5, frozenset({"B", "C"}): 7
}### 作为字典键值 
config = {frozenset(["read", "write"]): "admin",frozenset(["read"]): "guest"
}

缓存加速案例：函数结果缓存中，frozenset参数比tuple更高效
@lru_cache
def query_users(permissions: frozenset) -> list: ...

性能优化实战

数据去重选择策略：

小数据集（<1000项）：list(set(data))

大数据集：分批处理

chunks = [data[i:i+50000] for i in range(0, len(data), 50000)]
unique = set()
for chunk in chunks:unique |= set(chunk)

海量数据交并集加速：

使用集合运算代替循环 
a = set(large_data1)
b = set(large_data2)
common = a & b  # 比[i for i in a if i in b]快千倍# 分治优化内存 
def parallel_intersection(set1, set2):with ThreadPoolExecutor() as executor:chunks = [frozenset(chunk) for chunk in partition(set1, 4)]results = executor.map(lambda c: c & set2, chunks)return set().union(*results)