当前位置：首页 > news >正文

经典“绿叶”算法——SVM回归预测（SVR）算法及MATLAB实现

news 2025/11/1 18:59:44

一、从一个量化交易问题说起

在量化交易里，很多看似“分类”的判断，本质都是回归：我们更关心“涨多少/跌多少”、“下一根K线的收益率”、“收盘价与开盘价的价差”，而不是简单的涨或跌。实盘中常见的两类任务是：尾盘依据当日分时与资金/成交特征去预估收盘价或次日开盘价；日频/周频用多因子去预估未来一段的预期收益（Expected Return），据此做选股与权重分配。盘中亦可用盘口与成交微结构去预估短时价格微动，服务于择时与风控。

这些任务的共同点是：给定一组特征，输出一个连续数值（价格、收益、价差）。SVM 的回归形式——SVR（Support Vector Regression）特别适合这类问题：通过 ε-不敏感损失引入“容忍带”，对小误差不惩罚，在控制过拟合的同时刻画非线性关系，兼顾稳健与表达力。下面我们用可复现实验数据演示完整流程，方法可无缝迁移到股票回测与实盘信号。

二、从SVM分类到SVR回归：思想的转变

在之前的文章中，我们已经详细介绍了SVM分类的原理。SVM分类的核心思想是找到一个最优的超平面，使得两类数据之间的间隔最大化。那么，SVM能不能用于回归预测呢？答案是肯定的，这就是SVR（Support Vector Regression，支持向量回归）。

SVM分类 vs SVR回归：目标不同

让我们先来看看SVM分类和SVR回归的本质区别：

SVM分类vs回归对比

SVM分类的目标：找到一个分类边界，使得两类数据之间的间隔最大。支持向量是那些离分类边界最近的点，它们决定了边界的位置。

SVR回归的目标：找到一个拟合函数，使得大部分数据点都落在一个"容忍带"内。支持向量是那些落在容忍带外面的点，它们对模型有贡献。

可以看到，虽然都叫"支持向量"，但在分类和回归中，支持向量的含义完全不同：

在SVM分类中，支持向量在间隔边界上，是离分类线最近的点。

在SVR回归中，支持向量在容忍带外面，是离拟合线最远的点。

SVR的核心创新：ε-不敏感损失函数

SVR最大的创新在于提出了"ε-不敏感损失函数"（ε-insensitive loss function）。这是什么意思呢？

传统的回归算法（比如线性回归）会计算每个点的预测误差，然后最小化所有误差的平方和。也就是说，每个点都会对模型产生影响，即使误差很小的点也要计算损失。

但SVR的想法不一样。它说："我可以容忍一定范围内的误差。只要预测值和真实值的差距在ε以内，我就认为这个预测是完美的，不计算任何损失。"

这就像是在拟合线的两侧各画一条平行线，形成一个宽度为2ε的"管道"或"容忍带"。只要数据点落在这个管道里，就不计算损失；只有跑到管道外面的点，才需要计算损失并进行惩罚。

SVR容忍带原理

从上图可以清楚地看到：

绿色的点落在容忍带内，它们的损失为0，对模型没有影响。

红色的点落在容忍带外，它们是支持向量，需要计算损失。损失的大小等于实际误差减去ε。

这种设计有什么好处呢？

稀疏性：大部分点的损失为0，只有少数支持向量对模型有贡献，这使得模型更简洁。

鲁棒性：小的误差被忽略，模型不会被噪声数据过度影响。

泛化能力：通过控制ε的大小，可以平衡模型的复杂度和拟合精度。

三、SVR的关键参数

SVR有三个关键参数，它们共同决定了模型的性能：

1. 容忍带宽度 ε（epsilon）

ε控制了容忍带的宽度，也就是我们对误差的容忍程度。

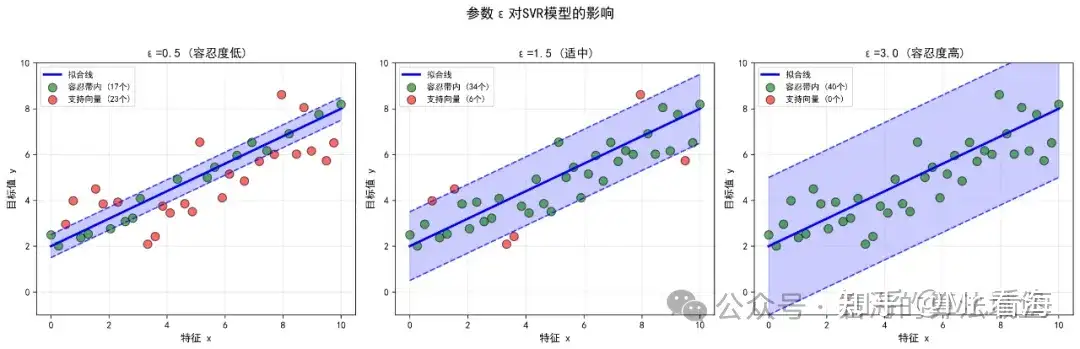
epsilon参数影响

从上图可以看到：

ε太小（如0.5）：容忍带很窄，大部分点都成为支持向量，模型复杂，容易过拟合。

ε适中（如1.5）：容忍带宽度合适，支持向量数量适中，模型性能最好。

ε太大（如3.0）：容忍带很宽，支持向量很少，模型过于简单，可能欠拟合。

2. 惩罚系数 C

C控制了对容忍带外的点的惩罚力度。C越大，对误差的惩罚越重，模型会努力让所有点都靠近拟合线；C越小，允许更多的点在容忍带外。

3. 核函数及其参数

当数据关系是非线性时，需要使用核函数将数据映射到高维空间。

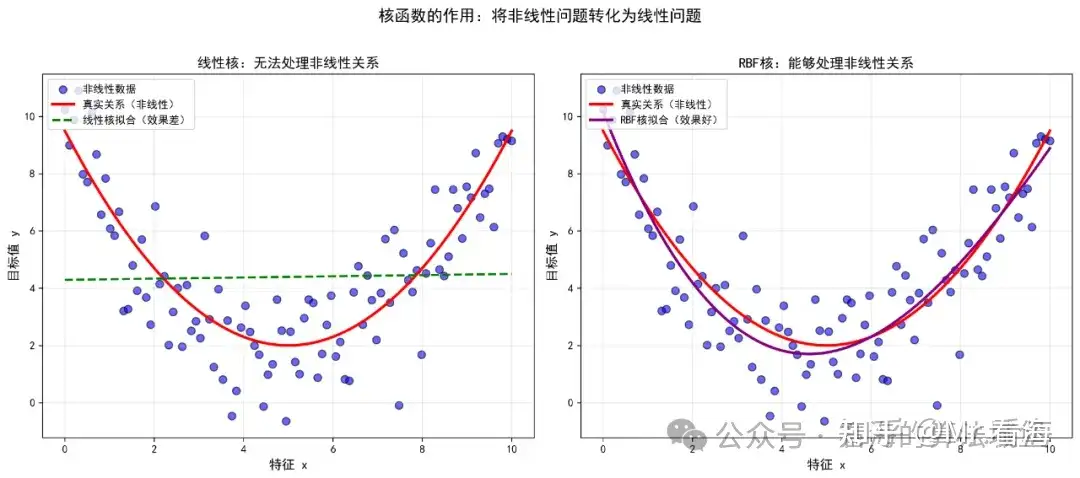
核函数作用

常用的核函数有：

线性核：适合线性关系的数据，计算速度快。

高斯核（RBF核）：最常用，能处理各种非线性关系，需要调整gamma参数。

多项式核：适合多项式关系的数据。

四、MATLAB实战：波士顿房价预测

下面我们通过一个完整的案例，看看如何用MATLAB实现SVM回归预测。

案例背景

我们使用经典的波士顿房价数据集，这个数据集包含506套房子的信息，每套房子有13个特征，我们的目标是预测房价（单位：千美元）。

13个特征分别是：

CRIM：城镇人均犯罪率
ZN：住宅用地比例
INDUS：非零售商用地比例
CHAS：是否靠近查尔斯河（0或1）
NOX：一氧化氮浓度
RM：住宅平均房间数
AGE：1940年之前建成的房屋比例
DIS：到波士顿五个中心区域的加权距离
RAD：辐射性公路的靠近指数
TAX：每10000美元的全值财产税率
PTRATIO：城镇师生比例
B：城镇黑人比例
LSTAT：人口中地位低下者的比例

步骤1：数据加载

首先，我们需要把数据加载到MATLAB中：

%% 1. 数据导入
% 加载波士顿房价数据集
data = load('housing.txt');
X = data(:, 1:13);  % 前13列为特征
Y = data(:, 14);    % 第14列为目标值（房价）fprintf('=== 数据集信息 ===\n');
fprintf('样本总数: %d\n', size(X, 1));
fprintf('特征维度: %d\n', size(X, 2));
fprintf('目标值范围: [%.2f, %.2f]\n\n', min(Y), max(Y));

运行后会显示：

=== 数据集信息 ===
样本总数: 506
特征维度: 13
目标值范围: [5.00, 50.00]

这说明我们有506套房子的数据，每套房子有13个特征，房价范围从5千美元到50千美元。

步骤2：参数设置

接下来设置SVM模型的参数：

%% 2. 调用核心函数进行SVM回归预测
% 设置参数
options.rTrain = 0.8;                    % 训练集比例80%
options.KernelFunction = 'linear';       % 核函数类型：线性核
options.BoxConstraint = 1;               % 箱式约束（惩罚系数C）：1
options.Epsilon = 0.1;                   % 容忍带宽度ε：0.1
options.Standardize = true;              % 数据标准化
options.mapflag = 'on';                  % 数据归一化
options.figflag = 'on';                  % 绘制结果图

参数说明：

rTrain = 0.8：80%的数据用于训练，20%用于测试

KernelFunction = 'linear'：使用线性核函数

BoxConstraint = 1：惩罚系数C设为1，平衡模型复杂度和误差

Epsilon = 0.1：容忍带宽度ε设为0.1，这是SVR的核心参数，控制ε-不敏感损失函数的容忍范围

Standardize = true：对数据进行标准化处理

mapflag = 'on'：对数据进行归一化到[0,1]区间

figflag = 'on'：自动生成可视化结果图

步骤3：模型训练与预测

调用封装好的核心函数进行训练和预测：

% 调用FunRegSVM函数
[foreData, foreDataTrain, info] = FunRegSVM(X, Y, options);

这一行代码就完成了数据预处理（归一化、标准化）、数据集划分（训练集和测试集）、SVM模型训练、模型预测、性能评估、结果可视化等全部工作。

步骤4：查看结果

程序运行后会在命令窗口显示详细的训练信息类似下边这样：

正在训练SVM回归模型...
核函数类型: linear
训练样本数: 404, 测试样本数: 102
SVM模型训练完成！=== 训练集性能评估 ===
MAE:   1.4757
MSE:   4.5359
RMSE:  2.1298
MAPE:  6.5631%
R2:    0.8486=== 测试集性能评估 ===
MAE:   1.6278
MSE:   5.9848
RMSE:  2.4464
MAPE:  5.7181%
R2:    0.8257图片已保存到 figure 文件夹

性能指标说明：

MAE（平均绝对误差）：平均每套房子预测误差约1.63千美元

RMSE（均方根误差）：考虑了大误差的惩罚，约2.45千美元

MAPE（平均绝对百分比误差）：平均误差占真实值的5.72%

R²（决定系数）：0.8257，说明模型解释了约82.57%的房价变化

同时，程序会自动生成4张可视化图片。

图1：训练集拟合效果