【研究生随笔】Pytorch中的卷积神经网络（2）

----------------------------------------------------------------接前文-----------------------------------------------------------
• 填充和步幅：前面讲到，假设输⼊形状为 n_h × n_w，卷积核形状为 k_h × k_w，那么输出形状将是 ( n_h − k_h + 1) × (n_w − k_w + 1)。因此，卷积的输出形状取决于输⼊形状和卷积核的形状。其次，影响输出现状的还包括填充和步幅。

• 填充：在应⽤多层卷积时，常常会丢失边缘像素。由于通常使⽤的是小卷积核，因此对于任何单个卷积，可能只会丢失⼏个像素。但随着应⽤了许多连续卷积层，累积丢失的像素数就多了。解决这个问题的简单⽅法即为填充（padding）：在输⼊图像的边界填充元素（通常填充元素是 0 ）。下面是对之前的例子做填充之后的样子：
  
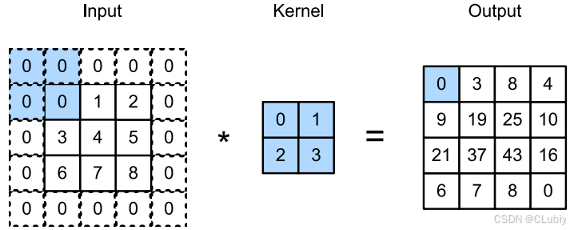
  如果我们添加 p_h ⾏填充（⼤约⼀半在顶部，⼀半在底部）和 p_w 列填充（大约左侧⼀半，右侧半），则输出形状将为：
  
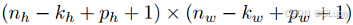
  也就是说输出的⾼度和宽度将分别增加 p_h 和 p_w 。
  在许多情况下，需要设置 p_h = k_h − 1 和 p_w = k_w − 1，使输⼊和输出具有相同的⾼度和宽度。这样可以在构建⽹络时更容易地预测每个图层的输出形状。假设 k_h 是奇数，那么将在⾼度的两侧填充 p_h/2 ⾏。如果k_h 是偶数，则⼀种可能性是在输⼊顶部填充 ⌈p_h/2⌉ ⾏，在底部填充 ⌊p_h/2⌋ ⾏。宽度也是同理。
  卷积神经⽹络中卷积核的⾼度和宽度通常为奇数。选择奇数的好处是，保持空间维度的同时，可以在顶部和底部填充相同数量的⾏，在左侧和右侧填充相同数量的列。使⽤奇数核和填充也提供了书写上的便利。对于任何⼆维张量 X，当满⾜： 1. 内核的⼤小是奇数； 2.所有边的填充⾏数和列数相同； 3. 输出与输⼊具有相同⾼度和宽度。则可以得出：输出 Y[i, j] 是通过以输⼊ X[i, j] 为中⼼，与卷积核进⾏互相关计算得到的。例子：

import torch
from torch import nn as nn
from d21 import torch as d21
# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):# 这里的(1,1)表示批量大小和通道数都是1X = X.reshape((1,1)+X.shape)Y = conv2d(X)
# 省略前两个维度：批量大小和通道return Y.reshape(Y.shape[2:])
# 清注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
print(comp_conv2d(conv2d, x).shape)

输出：

torch.size([8, 8])

当卷积内核的⾼度和宽度不同时，可以填充不同的⾼度和宽度，使输出和输⼊具有相同的⾼度和宽度。在如下例子中，使⽤⾼度为5，宽度为3的卷积核，⾼度和宽度两边的填充分别为2和1。如下：

conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))

• 步幅：在计算互相关时，卷积窗口从输⼊张量的左上⻆开始，向右下角滑动。在前⾯的例⼦中，默认每次滑动⼀个元素。但是，有时候为了⾼效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素，每次滑动元素的数量称为步幅（stride）。之前使用的都是高度或者宽度为1的步幅，如何使用更大的步幅呢。下面的例子是垂直步幅为3，⽔平步幅为2的⼆维互相关运算。着⾊部分是输出元素以及⽤于输出计算的输⼊和内核张量元素：可以看到，为了计算输出中第⼀列的第⼆个元素和第⼀⾏的第⼆个元素，卷积窗口分别向下滑动三⾏和向右滑动两列。但是，当卷积窗口继续向右滑动两列时，没有输出，因为输⼊元素不够了。
  
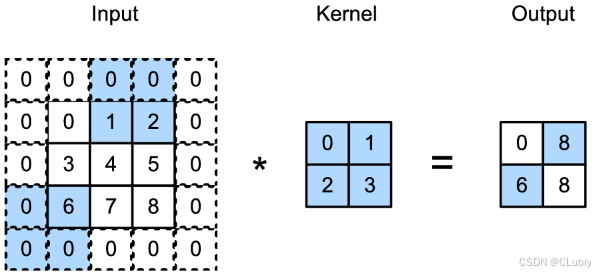
• 当垂直步幅为s_h 、⽔平步幅为s_w 时，输出形状为：
  
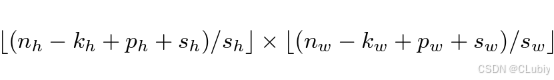
  如果设置了 p_h = k_h − 1 和 p_w = k_w − 1，则输出形状将简化为 ⌊(n_h + s_h − 1)/s_h⌋ × ⌊(n_w + s_w − 1)/s_w⌋。更进⼀步，如果输⼊的⾼度和宽度可以被垂直和⽔平步幅整除，则输出形状将为 (n_h/ s_h) × (n_w/ s_w)。

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, strid=2)
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))

当输⼊⾼度和宽度两侧的填充数量分别为p_h 和p_w 时，称之为填充(p_h，p_w)。当p_h = p_w = p时，填充是 p。同理，当⾼度和宽度上的步幅分别为 s_h 和 s_w 时，称之为步幅 (s_h，s_w)。当时的步幅为s_h = s_w = s 时，步幅为 s。默认情况下，填充为 0，步幅为 1。在真实实验中，很少使⽤不⼀致的步幅或填充，也就是说，通常都是 p_h = p_w 和 s_h = s_w 。

• summary：
  • 填充可以增加输出的⾼度和宽度。这常⽤来使输出与输⼊具有相同的⾼和宽。
  • 步幅可以减小输出的⾼和宽，例如输出的⾼和宽仅为输⼊的⾼和宽的（是⼀个⼤于的整数）。
  • 填充和步幅可⽤于有效地调整数据的维度。
• 多输入多输出通道：当添加通道时，模型中的输⼊和隐藏的表⽰都变成了三维张量。例如，每个RGB输⼊图像具有3hw的形状。将这个⼤小为3的轴称为通道（channel）维度。
  • 多输入通道：当输⼊包含多个通道时，需要构造⼀个与输⼊数据具有相同输⼊通道数⽬的卷积核，以便与输⼊数据进⾏互相关运算（也就是卷积运算）。假设输⼊的通道数为 c_i，那么卷积核的输⼊通道数也需要为 c_i 。如果卷积核的窗口形状是 k_h ×k_w，那么当 c_i = 1 时，可以把卷积核看作形状为 k_h ×k_w 的⼆维张量。
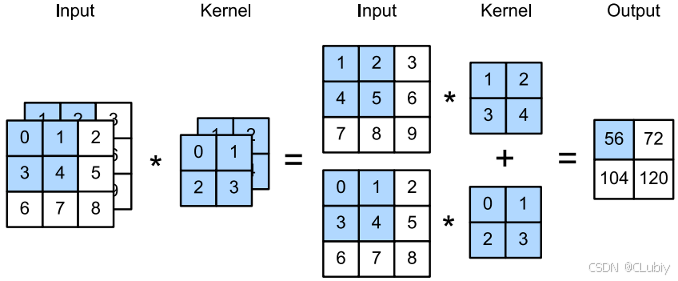
    当 c_i > 1 时，卷积核的每个输⼊通道将包含形状为 k_h ×k_w 的张量。将这些张量 c_i 连结在⼀起可以得到形状为 c_i × k_h ×k_w 的卷积核。由于输⼊和卷积核都有 c_i 个通道，可以对每个通道输⼊的⼆维张量和卷积核的⼆维张量进⾏互相关运算，再对通道求和（将 c_i 的结果相加）得到⼆维张量。这是多通道输⼊和多输⼊通道卷积核之间进⾏⼆维互相关运算的结果。
    下面是上面说一堆的案例：阴影部分是第⼀个输出元素以及⽤于计算这个输出的输⼊和核张量元素： (1×1+ 2×2+ 4×3+ 5×4)+ (0×0+ 1×1+ 3×2+ 4×3) = 56。
    
    代码：

def corr2d_multi_in(X, K):# 先遍历X”和K”的第0个维度（通道维度），再把他们加在一起return sum(d21.corr2d(x,k)for x,k in zip(X,K))X = torch.tensor([[0.0, 1.0, 2.0],[3.0, 4.9, 5.0],[6.0, 7.0, 8.0]
[[1.0, 2.0, 3.6],[4.0, 5.0, 6.8],[7.0, 8.0, 9.0]])
K = torch.tensor([[0.0, 1.0],[2.9, 3.0],[[1.0, 2.0],[3.0, 4.0]])
print(corr2d_multi_in(X, K))

○ 多输出通道：每⼀层有多个输出通道是⾄关重要的。在最流⾏的神经⽹络架构中，随着神经⽹络层数的加深，常会增加输出通道的维数，通过减少空间分辨率以获得更⼤的通道深度。直观地说，可以将每个通道看作是对不同特征的响应。而现实可能更为复杂⼀些，因为每个通道不是独⽴学习的，而是为了共同使⽤而优化的。因此，多输出通道并不仅是学习多个单通道的检测器。
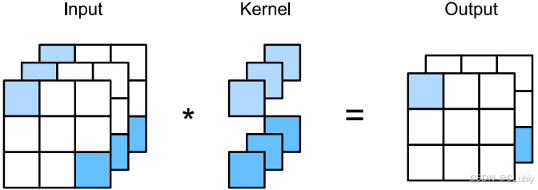
⽤ c_i 和 c_o 分别表⽰输⼊和输出通道的数⽬，并让k_h 和k_w 为卷积核的⾼度和宽度。为了获得多个通道的输出，我们可以为每个输出通道创建⼀个形状为 c_i ×k_h ×k_w 的卷积核张量，这样卷积核的形状是 c_o ×c_i ×k_h ×k_w 。在互相关运算中，每个输出通道先获取所有输⼊通道，再以对应该输出通道的卷积核计算出结果。

def corr2d_multi in_out(X, K):
# 迭代"K"的第0个维度，每次都对输入"X"执行互相关运算。
# 最后将所有结果郜叠加在一起
return torch.stack([corr2d_multi_in(X, k)for k in K], 0)# 通过将该张量K与K+1(K中每个元素加1)和K+2连接起来，构造了一个具有3个榆出通道的卷积核
K = torch.stack((K, K+1, K+2), 0) # K.shape = torch.Size([3,2,2,2])
print(corr2d_multi_in_out(X, K))

○ 1 × 1卷积层：1 × 1 卷积，即 k_h= k_w = 1，看起来似乎没有多⼤意义。毕竟，卷积的本质是有效提取相邻像素间的相关特征，而 1 × 1 卷积显然没有此作⽤。尽管如此， 1 × 1 仍然⼗分流⾏，时常包含在复杂深层⽹络的设计中。因为使⽤了最小窗口， 1 × 1 卷积失去了卷积层的特有能⼒——在⾼度和宽度维度上，识别相邻元素间相互作⽤的能⼒。其实 1 × 1 卷积的唯⼀计算发⽣在通道上。
输⼊和输出具有相同的⾼度和宽度（1 × 1），输出中的每个元素都是从输⼊图像中同⼀位置的元素的线性组合。我们可以将 1 × 1 卷积层看作是在每个像素位置应⽤的全连接层，以 c_i 个输⼊值转换为c_o 个输出值。因为这仍然是⼀个卷积层，所以跨像素的权重是⼀致的。同时， 1 × 1 卷积层需要的权重维度为 c_i × c_o ，再额外加上⼀个偏置。

代码：

def corr2d_multi in_out_1x1(X, K):c_i, h, w = X.shapec_o = K.shape[e]X = x.reshape((c_i,h, w))K = K.reshape((c_o,c_i))# 全连接层中的矩阵乘法Y = torch.matmul(K,X)return Y.reshape((c_o,h,w))X = torch.normal(0,1,(3,3,3))
K = torch.normal(0,1,(2,3,1,1))
Y1 = corr2d_multi_in_out_1x1(X,K)
Y2 = corr2d_multiin_out(X,K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6

○ Summary
-多输⼊多输出通道可以⽤来扩展卷积层的模型。
-当以每像素为基础应⽤时， 1 × 1 卷积层相当于全连接层。
-1 × 1 卷积层通常⽤于调整⽹络层的通道数量和控制模型复杂性。
• 池化层
通常当处理图像时，希望模型可以逐渐降低隐藏表⽰的分辨率，聚集信息，随着在神经⽹络中，层叠的上升，每个神经元对其敏感的输⼊就越⼤。而机器学习任务通常会跟全局图像的问题有关（例如，图像里有狗吗？是什么狗？），所以最后⼀层的神经元应该对整个输⼊全局敏感。通过逐渐聚合信息，⽣成越来越粗糙的映射，最终实现学习全局表⽰的⽬标，同时将卷积图层的所有优势保留在中间层。
所以需要引入池化（pooling）层，它具有双重⽬的：降低卷积层对位置的敏感性，同时降低对空间降采样表⽰的敏感性。
○ 最大池化层和平均池化层：与卷积层类似（kernel），池化层运算符由⼀个固定形状的窗口组成，该窗口根据其步幅⼤小在输⼊的所有区域上滑动，为窗口遍历的每个位置计算⼀个输出。然而，不同于卷积层中输⼊与卷积核之间的互相关计算，池化层是不包含参数的。并且，池运算符是确定的，通常计算池化窗口中所有元素的最⼤值（最⼤池化层（maximum pooling））或平均值（平均池化层（average pooling））。
与互相关运算符⼀样，池化窗口从输⼊张量的左上⻆开始，从左到右、从上到下的在输⼊张量内滑动。在池化窗口到达的每个位置，它计算该窗口中输⼊⼦张量的最⼤值或平均值，具体取决于是使⽤了最⼤池化层还是平均池化层。如下图的最大池化层：

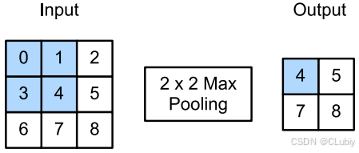
池化窗口形状为 p × q 的池化层称为 p × q 池化层，池化操作称为 p × q 池化。代码实现一下池化层的正向传播（没有添加卷积核）：

def MyPool(X,pool_size,mode = 'max'):p_h, p_w = pool_sizeY = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))for i in range(Y.shape[0]):for j in range(Y.shape[1]):if mode ='max':Y[i, j] = X[i:i + p_h, j:j + p_w].max()elif mode ='avg':Y[i, j] = X[i:i + p_h, j:j + p_w].mean()return Y
# 测试一下
X = torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
prit(yPoo1(X,(2,2)) # 可以再加个参数选择最大值或者平均值（因为形参中有设置默认值，所以可以不传这个参数）

填充和步幅：可以说是一个东西，这俩跟卷积层是一模一样的。

poo12d = nn.MaxPool2d(3, paddings=1, stride=2)

○ Summary
-对于给定输⼊元素，最⼤池化层会输出该窗口内的最⼤值，平均池化层会输出该窗口内的平均值。
-池化层的主要优点之⼀是减轻卷积层对位置的过度敏感。
-可以指定池化层的填充和步幅。
-使⽤最⼤池化层以及⼤于 1 的步幅，可减少空间维度（如⾼度和宽度）。
-池化层的输出通道数与输⼊通道数相同。
• Summary
○ 卷积神经⽹络（CNN）是⼀类使⽤卷积层的⽹络。
○ 在卷积神经⽹络中，一般组合使⽤卷积层、⾮线性激活函数和池化层。
○ 为了构造⾼性能的卷积神经⽹络，通常对卷积层进⾏排列，逐渐降低其表⽰的空间分辨率，同时增加通道数。
在传统的卷积神经⽹络中，卷积块编码得到的表征在输出之前需由⼀个或多个全连接层进⾏处理。