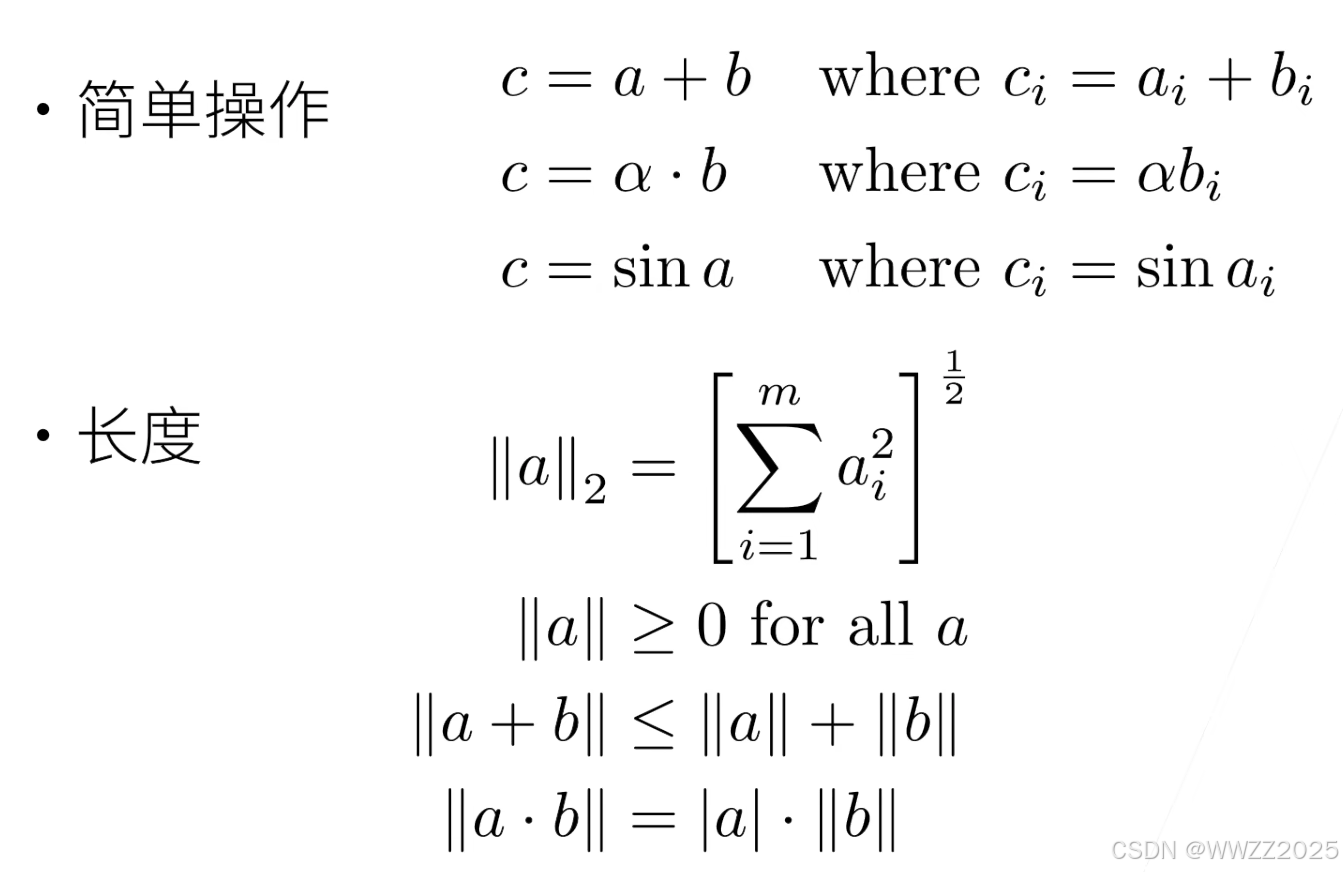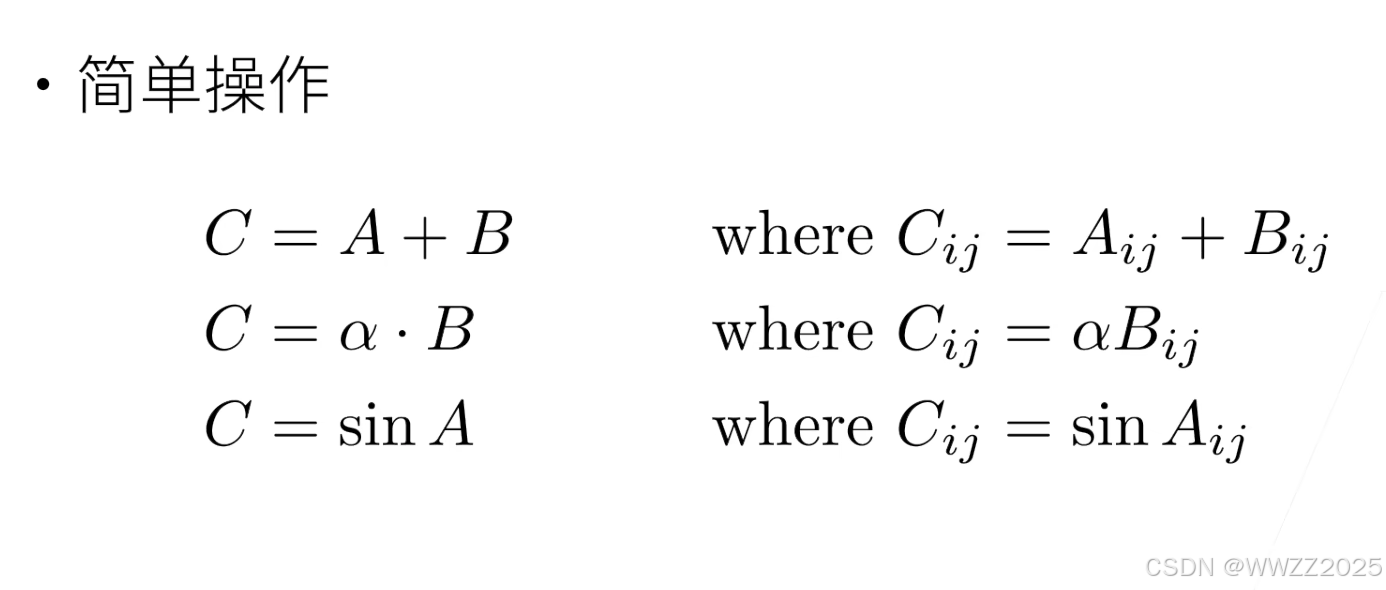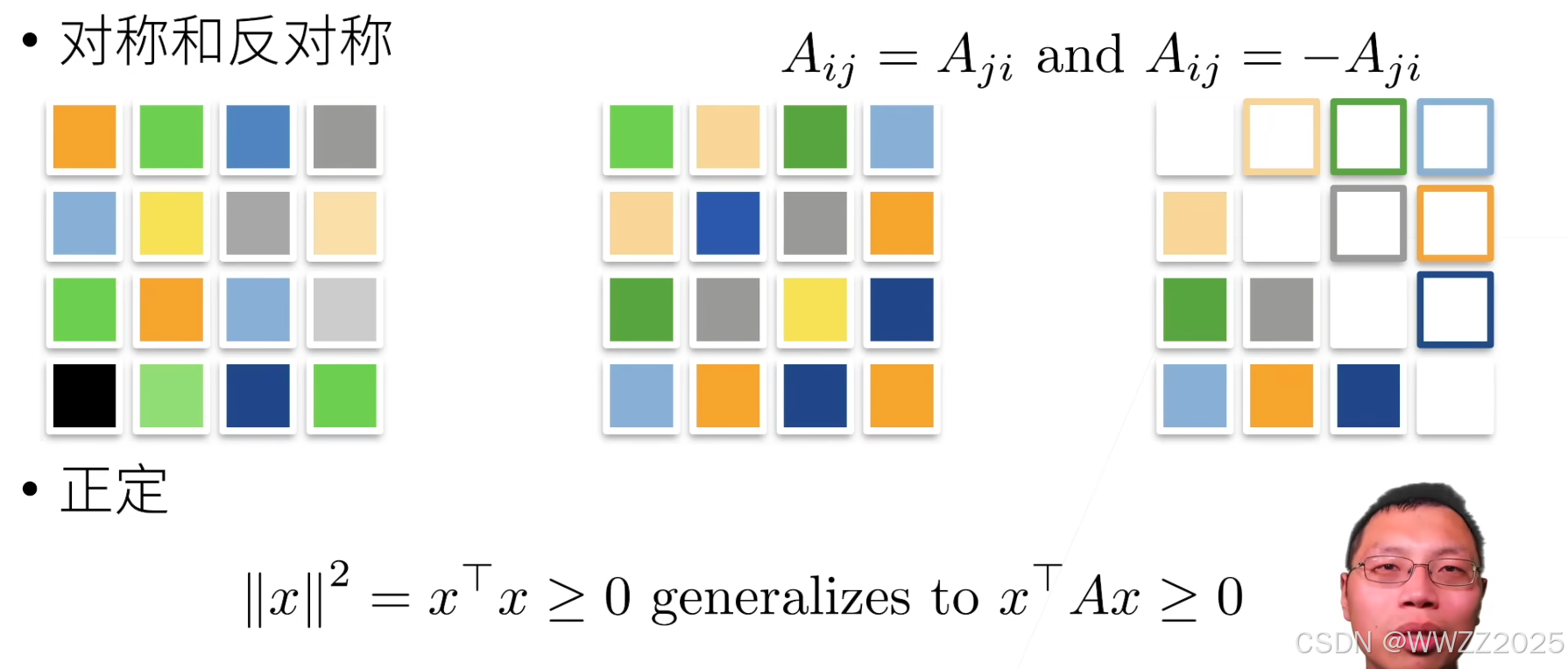当前位置：首页 > news >正文

快速上手大模型：深度学习2（实践：深度学习基础、线性回归）

news 2025/10/28 12:27:55

目录

1 环境配置

1.1 安装miniconda

1.2 创建Python3.8环境

1.3 安装PyTorch、Jupyter、d2l

1.4 进入和退出虚拟环境

2 下载课程资源

3 调用jupyter notebook

4 数据操作

4.1 广播机制(broadcasting mechanism)

4.2 数据预处理

4.2.1 创建数据集

4.2.2 缺失数据处理

4.2.3 转为张量格式

5 线性代数

5.1 常用运算

5.1.1 标量

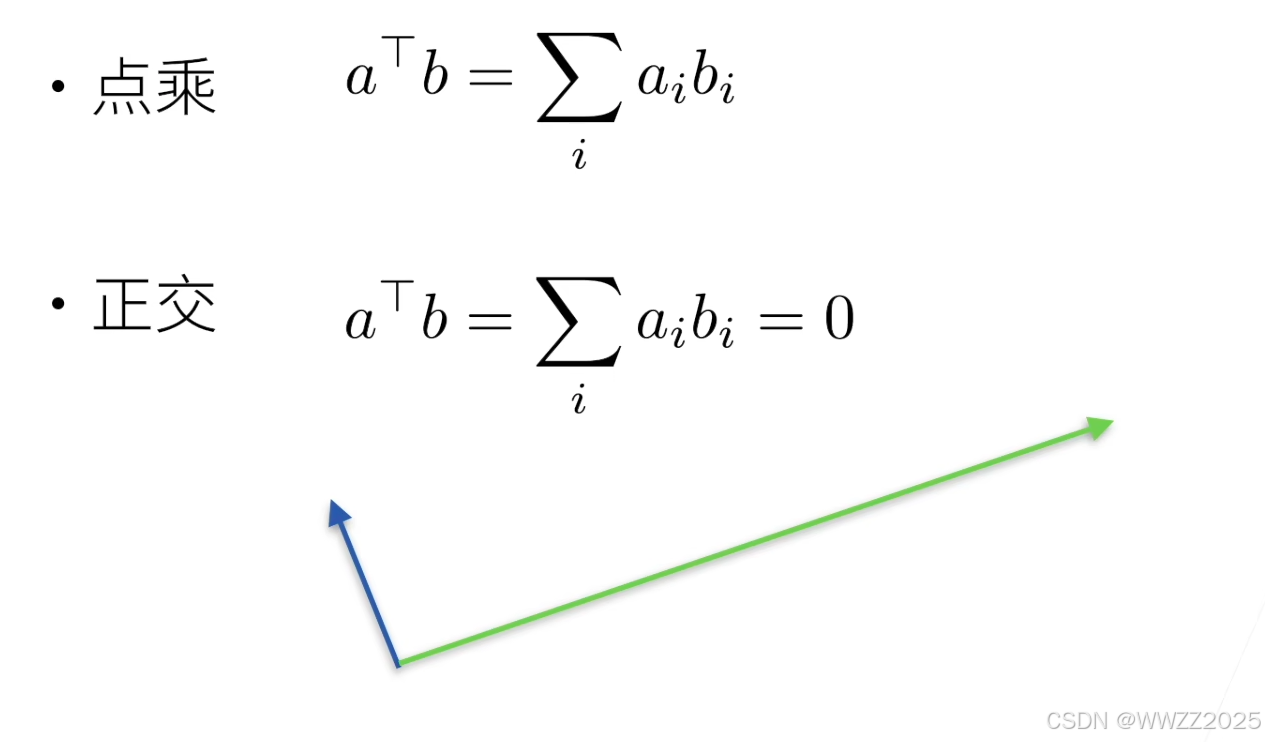
5.1.2 向量

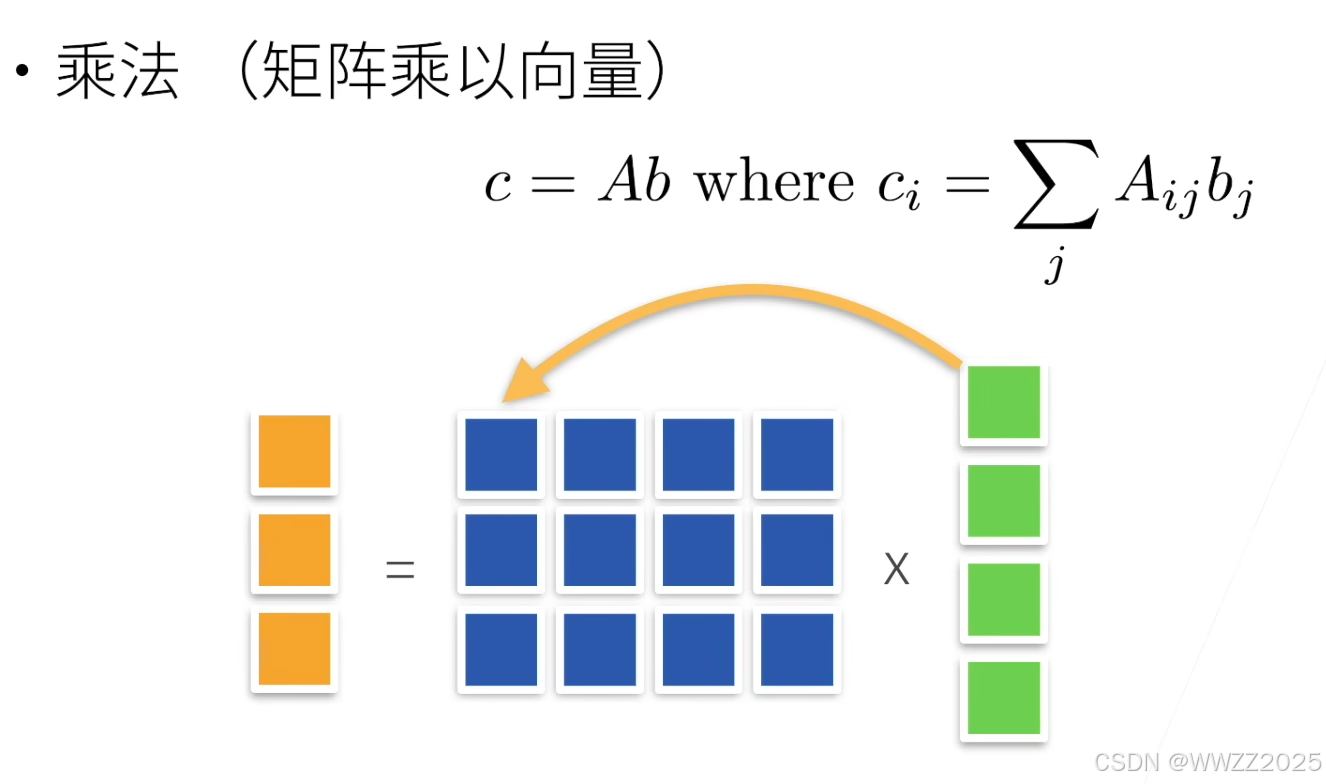
5.1.3 矩阵

5.2 代码实践

5.2.1 标量

5.2.2 向量

5.2.3 特定轴

求和

保持维度

编辑

5.2.4 自动求导

6 线性回归

6.1 构建模型

6.2 生成小批量

6.3 定义初始化模型参数

6.4 定义损失函数

6.5 定义优化算法

6.6 训练过程

6.7 上述步骤的简洁实现

实践部分根据李沫大佬课程，配合李宏毅理论学习。

课程链接：https://courses.d2l.ai/zh-v2/

书籍：https://zh-v2.d2l.ai/

1 环境配置

博主使用双系统，在Ubuntu20.04上进行实践。

1.1 安装miniconda

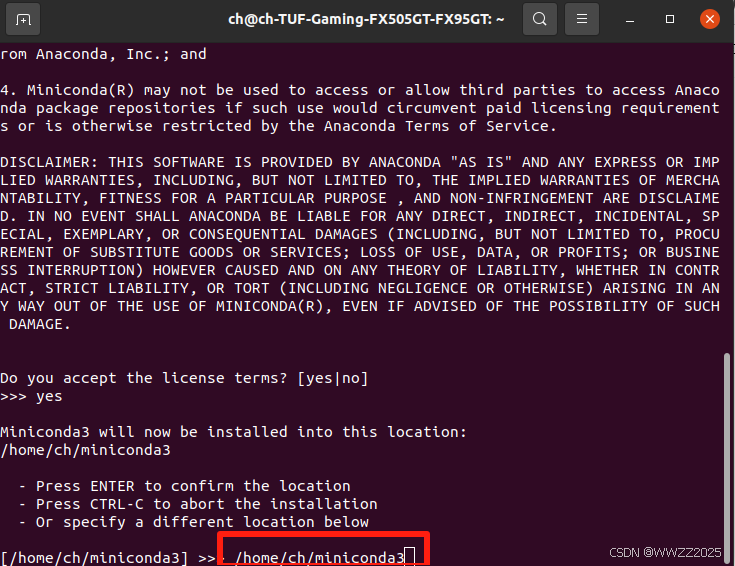
#下载miniconda
wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh
#运行安装脚本
bash Miniconda3-latest-Linux-x86_64.sh
（1）回车+yes，选择安装路径：

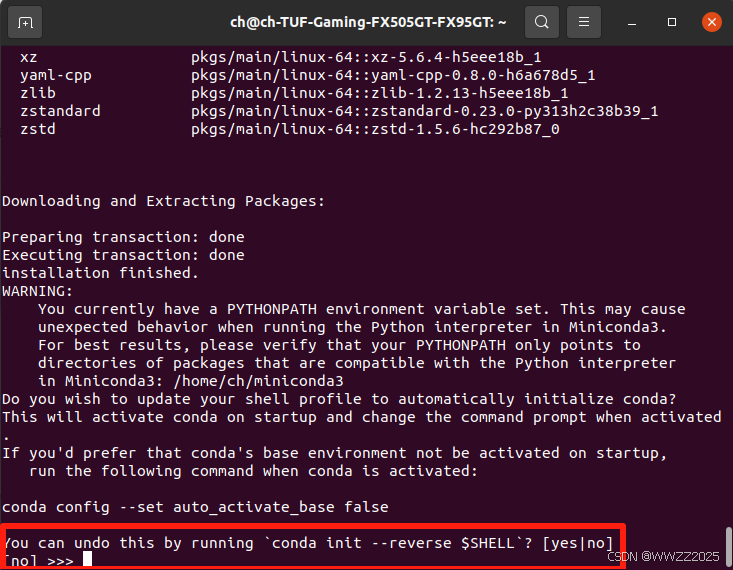
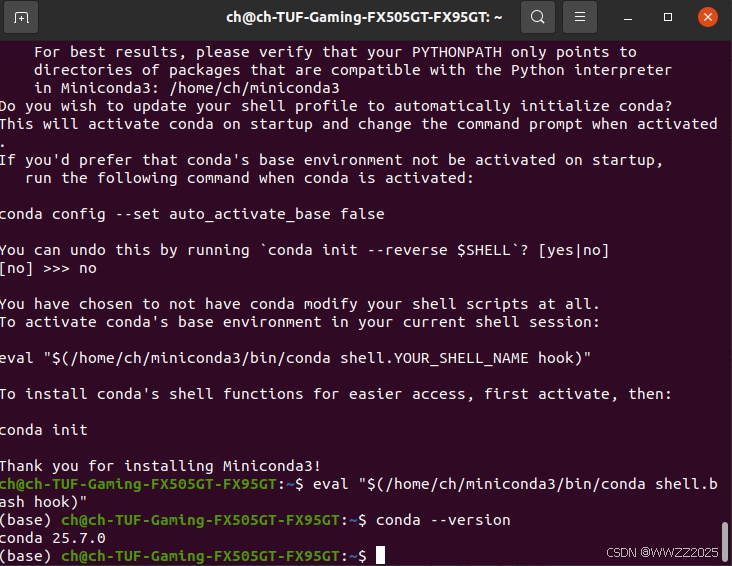
（2）选择是否开机时自启动miniconda，此处都行，看个人习惯，博主选择no，后续启动miniconda命令如下，注意修改为自己的路径：
eval "$(/home/ch/miniconda3/bin/conda shell.bash hook)"
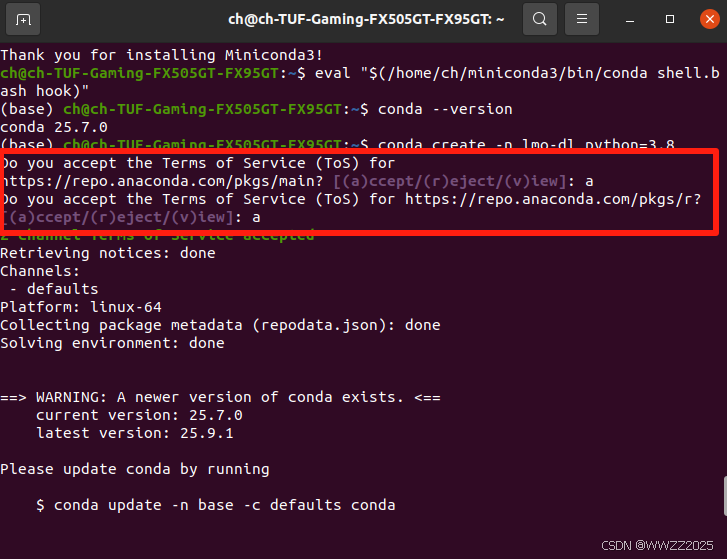
（3）显示版本信息表明安装成功

1.2 创建Python3.8环境

因博主使用Ubuntu20.04版，自带Python3.8，故直接创建环境即可。
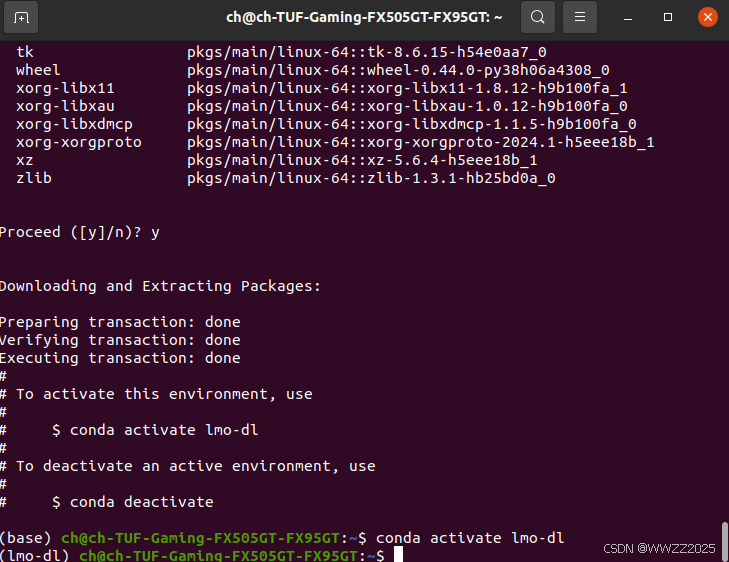
# 创建隔离环境
conda create -n lmo-dl python=3.8# 激活环境
conda activate lmo-dl
（1）全部接受，a+回车，后面yes

（2）环境配置成功：

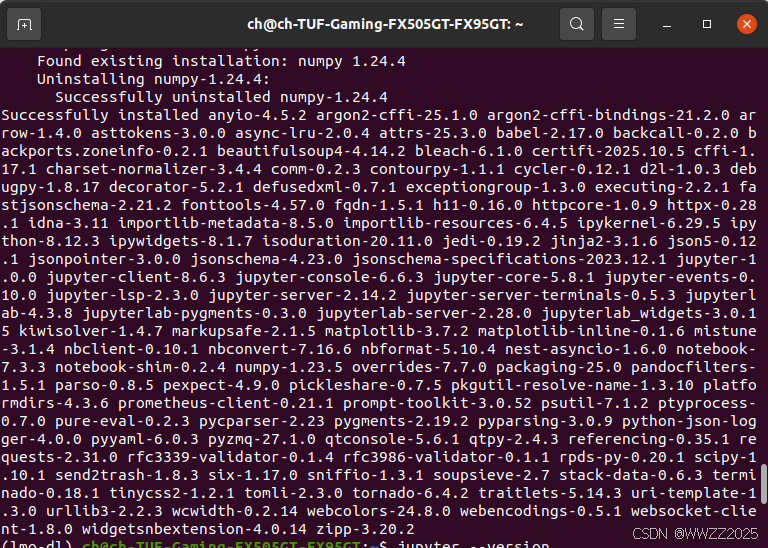
1.3 安装PyTorch、Jupyter、d2l

#安装 PyTorch（课程推荐版本）
pip install torch==1.10.0 torchvision#安装
pip install jupyter d2l torch torchvision

1.4 进入和退出虚拟环境

#进入虚拟环境
conda activate lmo-dl#进入虚拟环境base
conda activate base#退出虚拟环境
conda deactivate

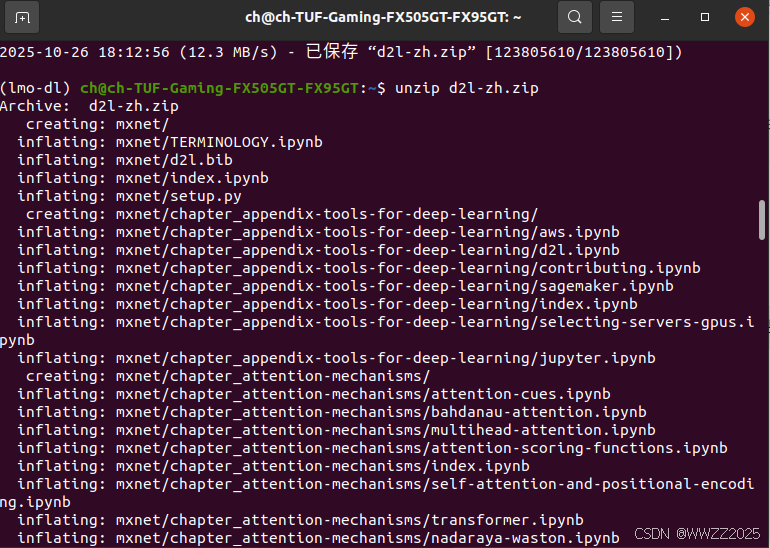
2 下载课程资源

wget https://zh-v2.d2l.ai/d2l-zh.zip
unzip d2l-zh.zip

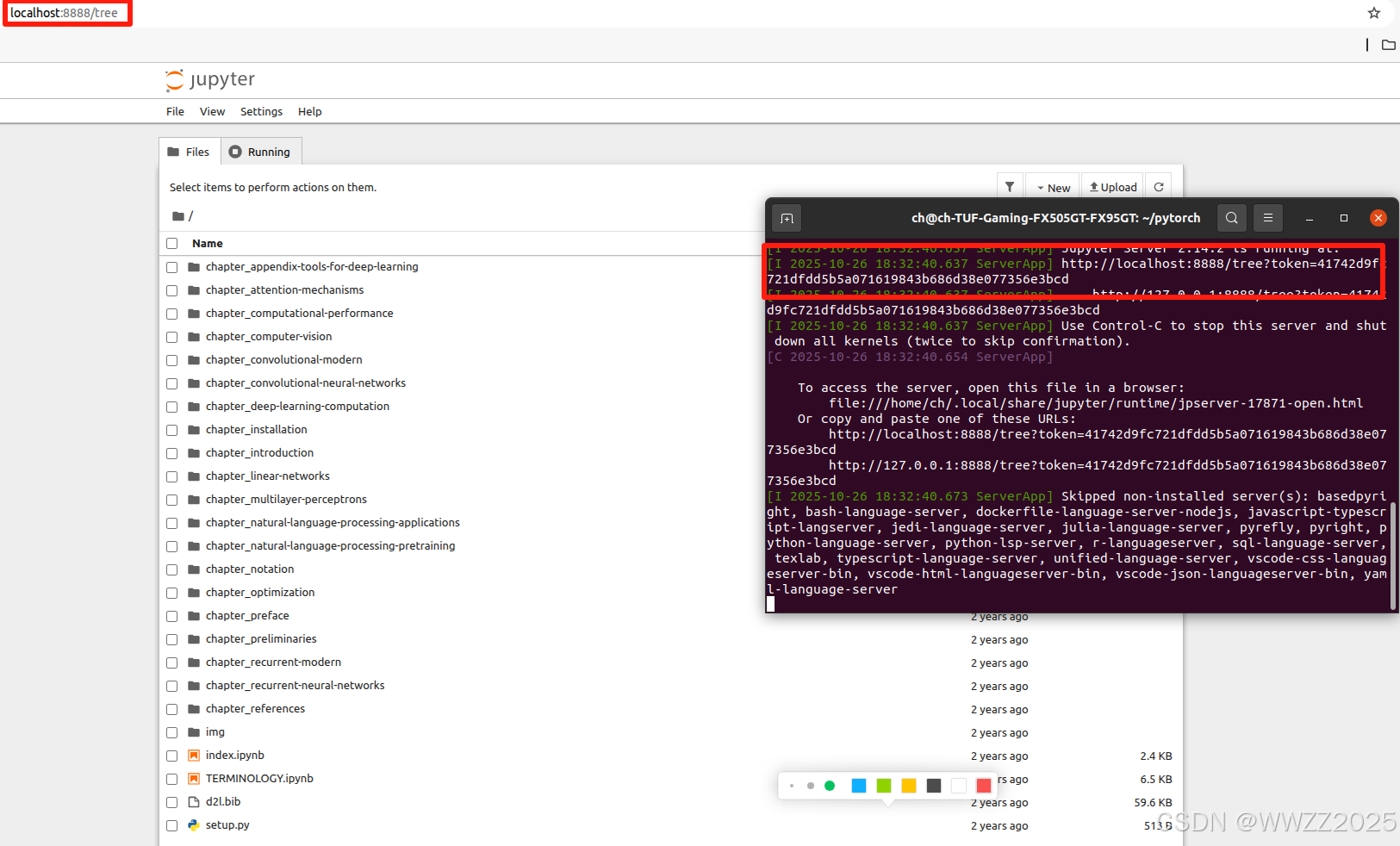
3 调用jupyter notebook

把本地电脑的文件夹映射到 Jupyter Notebook 的工作目录，让 Jupyter Notebook 在浏览器里能直接看到你本地的文件夹。

博主输入指令后可以直接跳转网页，如没有可以查看终端中网页链接，图中已用红框标记。
#将当前注册为Jupyter kernel
conda activate lmo-dl
conda install ipykernel
python -m ipykernel install --user --name lmo-dl --display-name "Python (lmo-dl)"#打开jupyter notebook
cd ~/pytorch
jupyter notebook
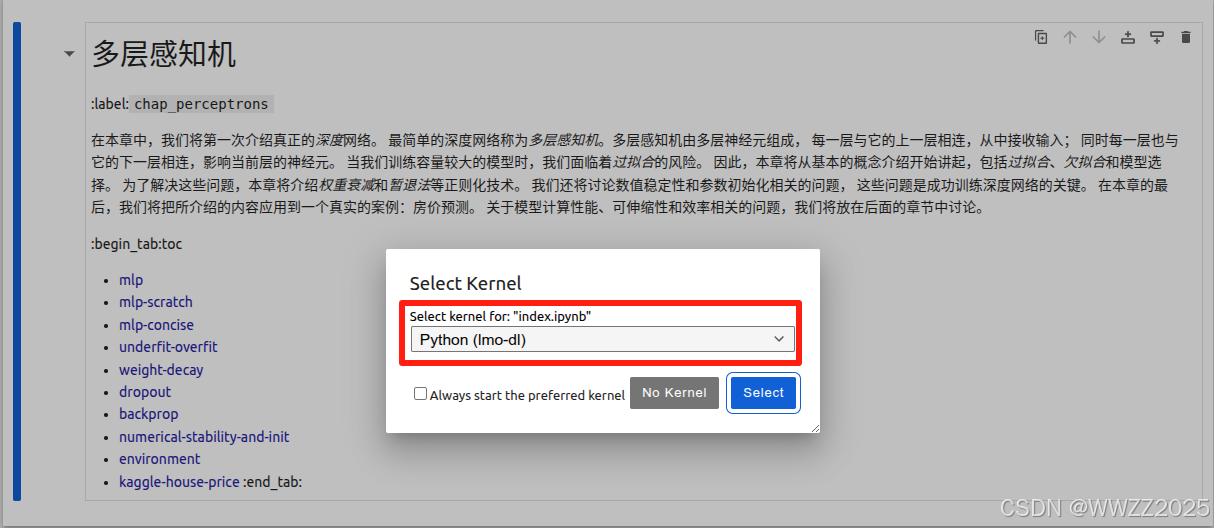
选择刚才注册的Kernel：

4 数据操作

4.1 广播机制(broadcasting mechanism)

4.2 数据预处理

4.2.1 创建数据集

人工创建数据集，并储存在csv（逗号分隔符）文件

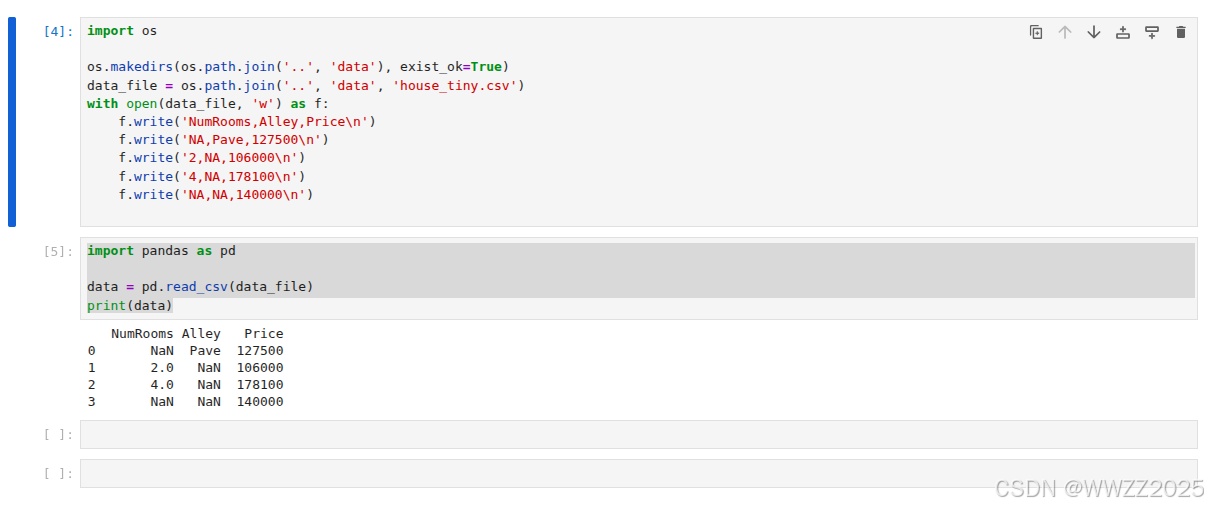
import osos.makedirs(os.path.join('..','data'),exist_ok=True)
data_file = os.path.join('..','data', 'house_tiny.csv')
with open(data_file, 'w') as f:f.write（'NumRooms,Alley,Price\n'）   #列名f.write（'NA,Pave,127500\n'）  #每行表示一个样本数据f.write（'2,NA,106000\n'）f.write（'4,NA,178100\n'）f.write（'NA,NA,140000\n'）

从创建的csv文件中加载原始数据集

import pandas as pddata = pd.read_csv(data_file)
print(data)

输出

4.2.2 缺失数据处理

对于上面缺失的数据，可以插值、删除处理，如下是插值处理（取均值）
inputs, outputs = data.iloc[:, 0:2],data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean(numeric_only=True))
inputs = pd.get_dummies(inputs, dummy_na=True,dtype=int)
print(inputs)

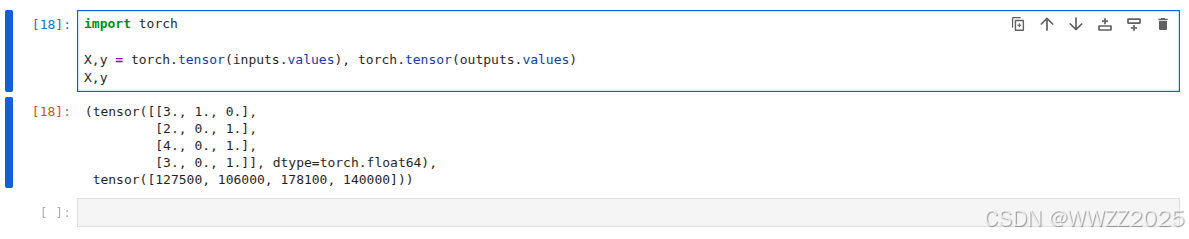
4.2.3 转为张量格式

import torchX,y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X,y

5 线性代数

5.1 常用运算

5.1.1 标量

5.1.2 向量

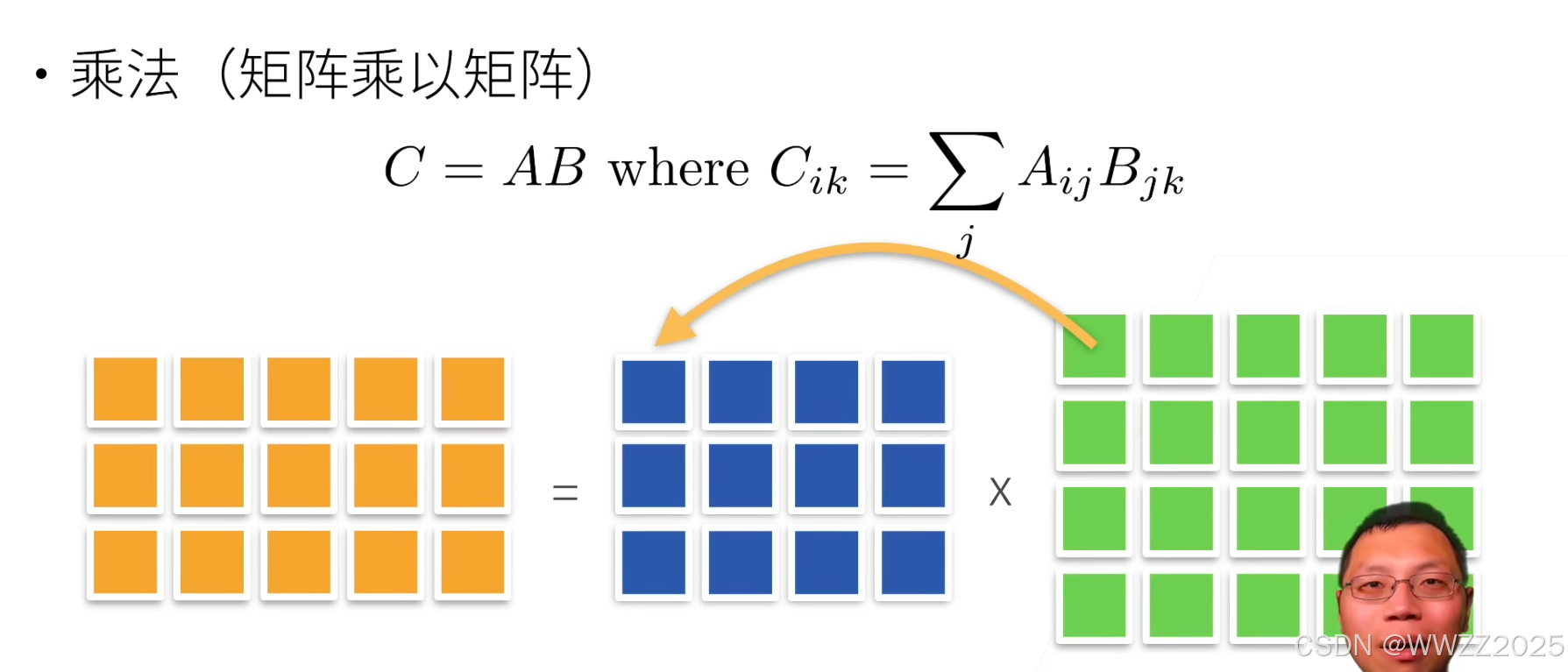
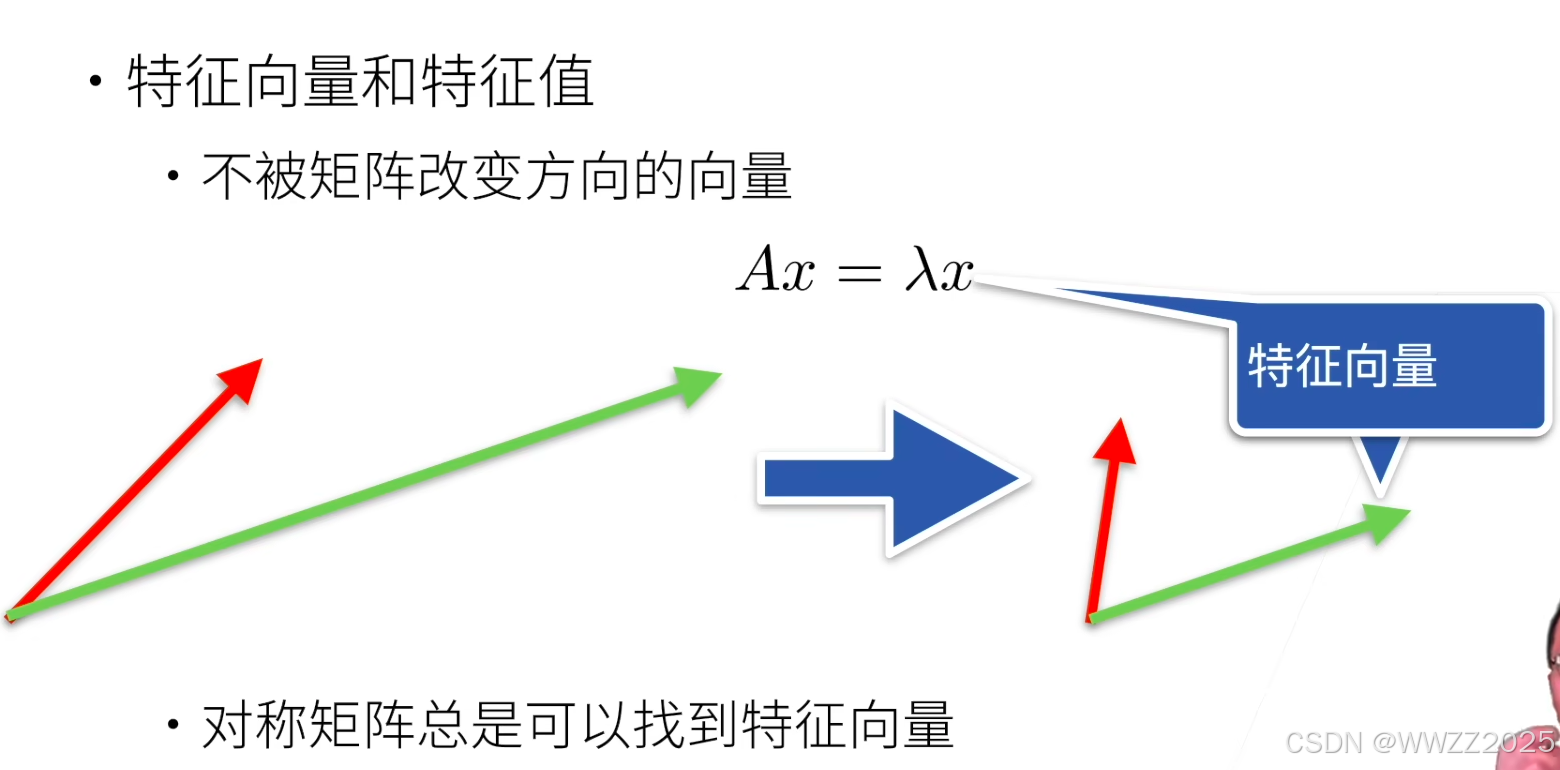
5.1.3 矩阵

5.2 代码实践

5.2.1 标量

import torchx = torch.tensor([3.0])
y = torch.tensor([2.0])x+y,x*y,x/y,x**y

5.2.2 向量

（1）将向量视为标量值组成的列表
x = torch.arange(4)
x
（2）通过张量索引访问任一元素

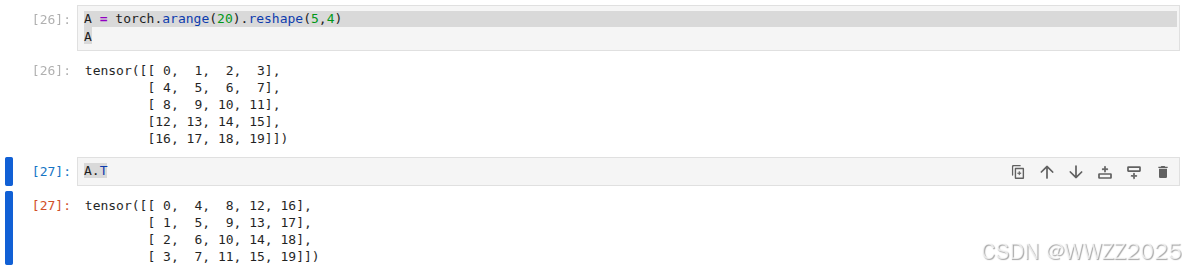
（3）矩阵转置
A = torch.arange(20).reshape(5,4)
A
A.T
（4）对称矩阵
B = torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
B
B == B.T
（5）常规运算

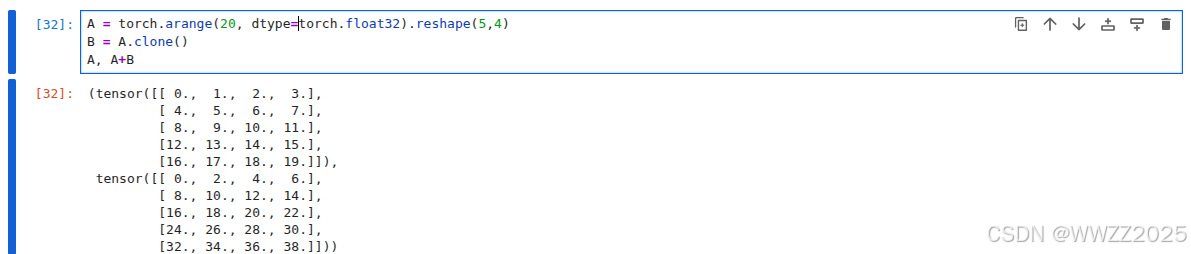
加法：
A = torch.arange(20, dtype=torch.float32).reshape(5,4)
B = A.clone()
A, A+B
向量积：
A = torch.tensor([[1, 2], [3, 4]], dtype=torch.float32)
x = torch.tensor([1.0, 2.0], dtype=torch.float32)
torch.mv(A, x)
范数：
u = torch.tensor([3.0, -4.0])
torch.norm(u)
佛罗贝尼乌斯范数(Frobenius norm)：
torch.norm(torch.ones((4,9)))

5.2.3 特定轴

求和

代码中创建了两个5*4的矩阵，对维度1（即行）进行求和，a向量变为2*4
import torcha = torch.ones((2,5,4))
a.sum(axis=1).shape

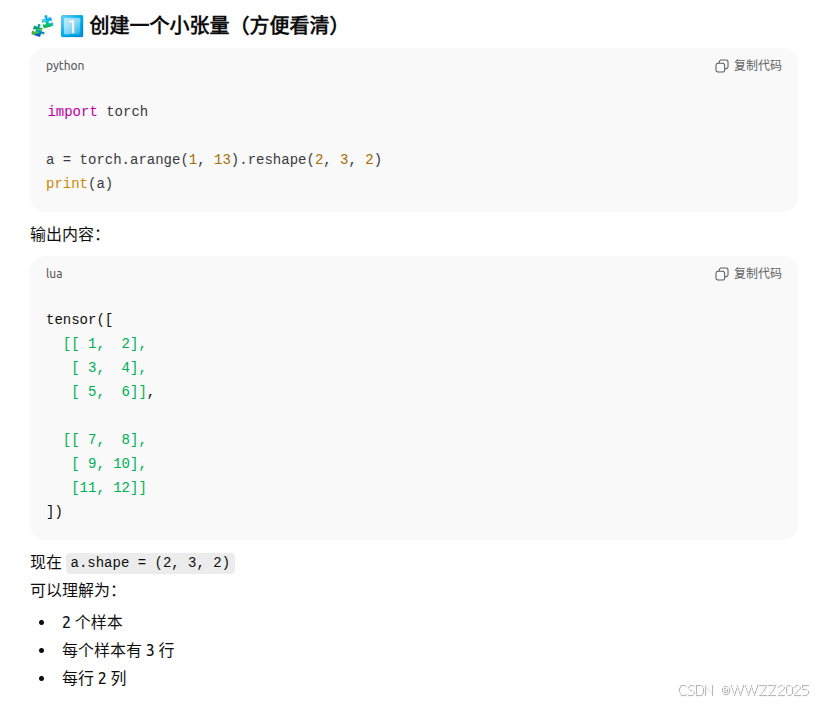
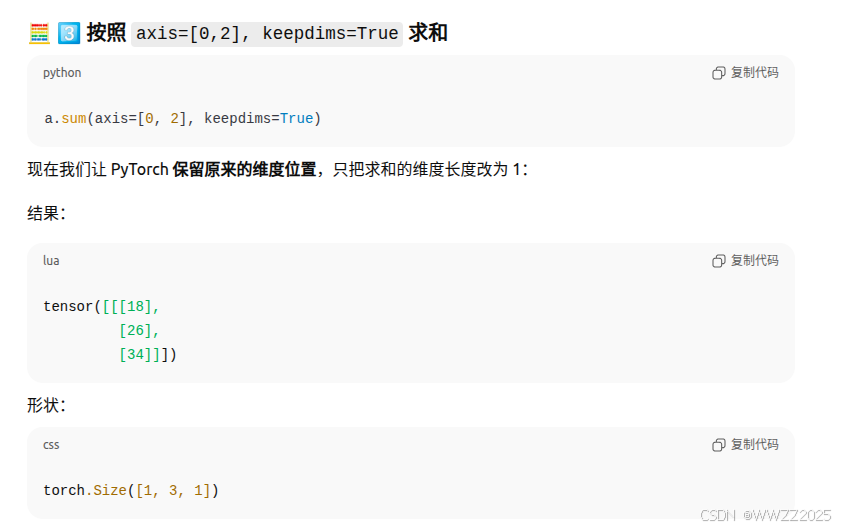
保持维度

举例：

5.2.4 自动求导

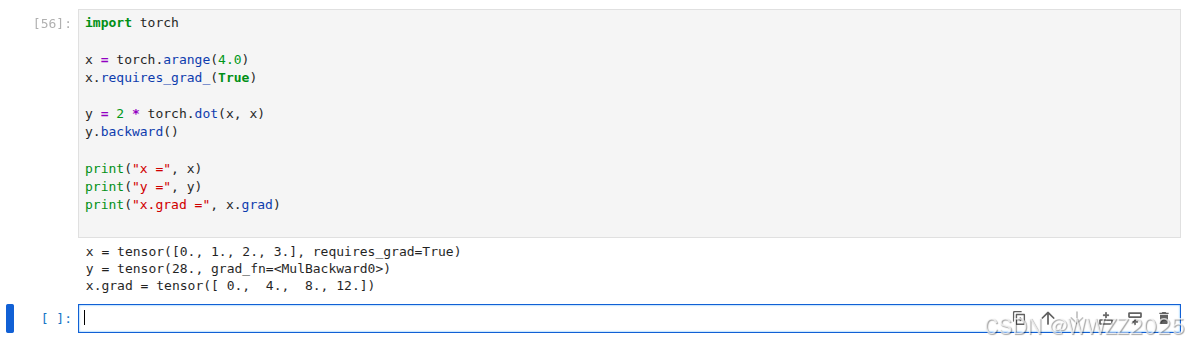
import torchx = torch.arange(4.0)
x.requires_grad_(True)y = 2 * torch.dot(x, x)
y.backward()print("x =", x)
print("y =", y)
print("x.grad =", x.grad)

反向传播：

x.grad.zero_()  #梯度清零
y = x*x
y.sum().backward() #反向传播，其实就是对y求导，y'=2x
x.grad

6 线性回归

线性回归，详见1、2

https://blog.csdn.net/weixin_45728280/article/details/153348420?spm=1011.2415.3001.5331

优化算法，详见3梯度下降

https://blog.csdn.net/weixin_45728280/article/details/153348420?spm=1011.2415.3001.5331

6.1 构建模型

构造人造数据集，线性模型参数 $w=[2,-3,4]^{T},b=4.2$ ，噪声 $\epsilon$ ，数据集及其标签 $y=Xw+b+\epsilon$ 。

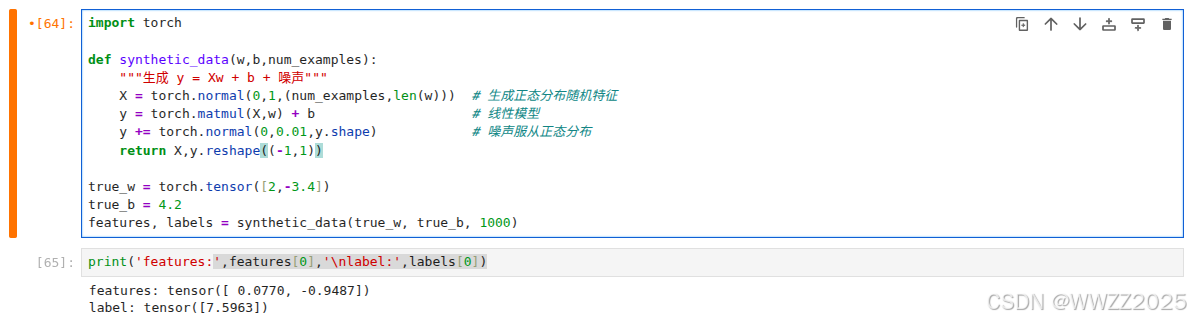
构建模型：

import torchdef synthetic_data(w,b,num_examples):"""生成 y = Xw + b + 噪声"""X = torch.normal(0,1,(num_examples,len(w)))  # 生成正态分布随机特征y = torch.matmul(X,w) + b                    # 线性模型y += torch.normal(0,0.01,y.shape)            # 噪声服从正态分布return X,y.reshape((-1,1))true_w = torch.tensor([2,-3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

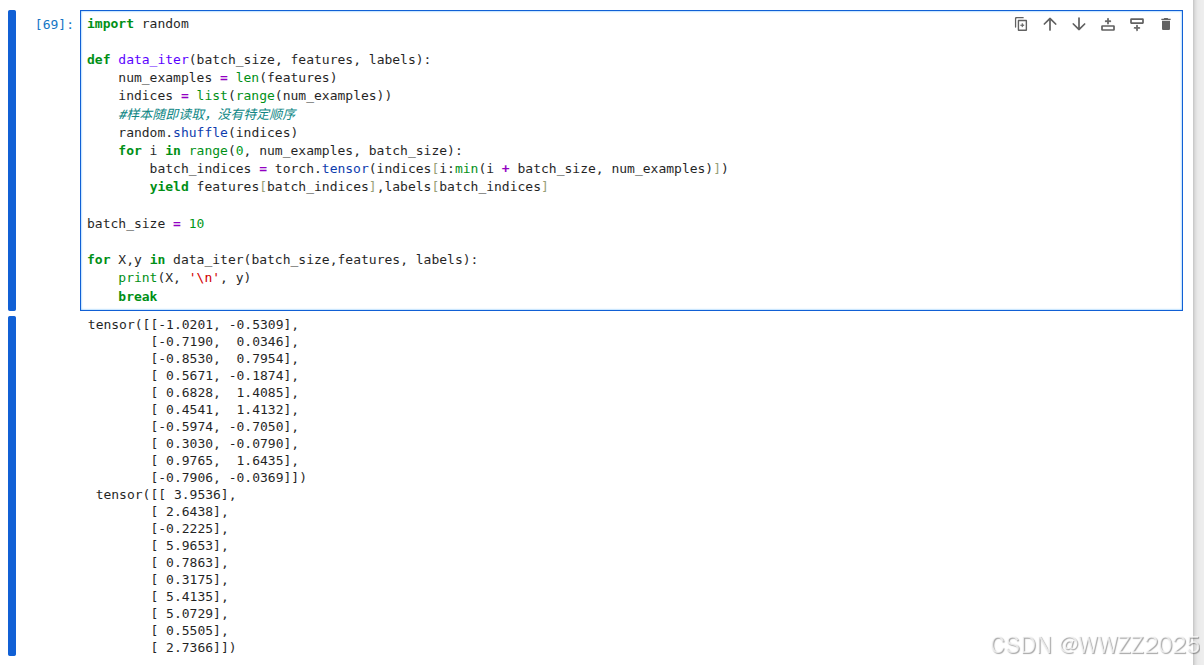
6.2 生成小批量

import randomdef data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))#样本随即读取，没有特定顺序random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])yield features[batch_indices],labels[batch_indices]batch_size = 10for X,y in data_iter(batch_size,features, labels):print(X, '\n', y)break

6.3 定义初始化模型参数

w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)def linreg(X,w,b):"""线性回归模型"""return torch.matmul(X, w) + b

6.4 定义损失函数

def squared_loss(y_hat, y):"""均方损失"""return(y_hat - y.reshape(y_hat.shape))**2 / 2

6.5 定义优化算法

def sgd(params, lr, batch_size):"""小批量随机梯度下降"""with torch.no_grad():   #不记录梯度计算过程for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()

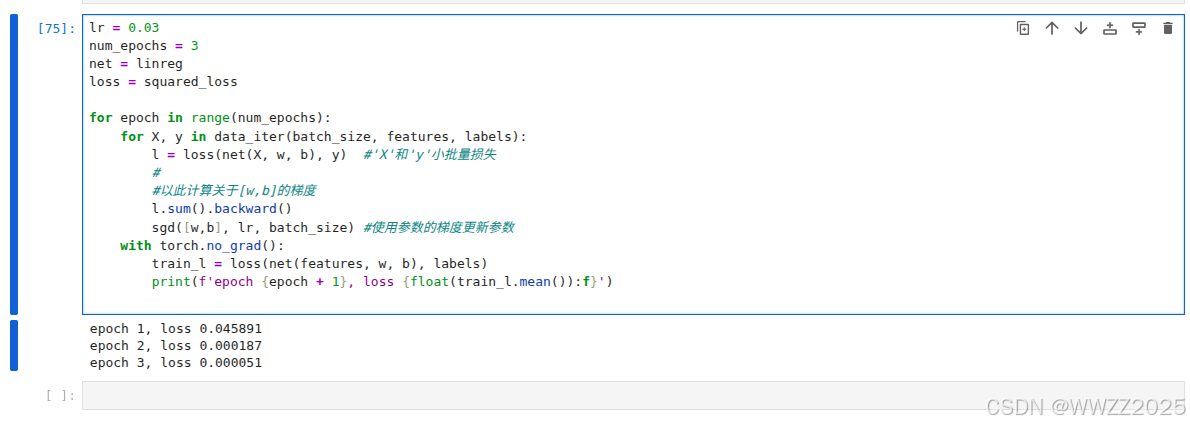
6.6 训练过程

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_lossfor epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y)  #'X'和'y'小批量损失##以此计算关于[w,b]的梯度l.sum().backward()sgd([w,b], lr, batch_size) #使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

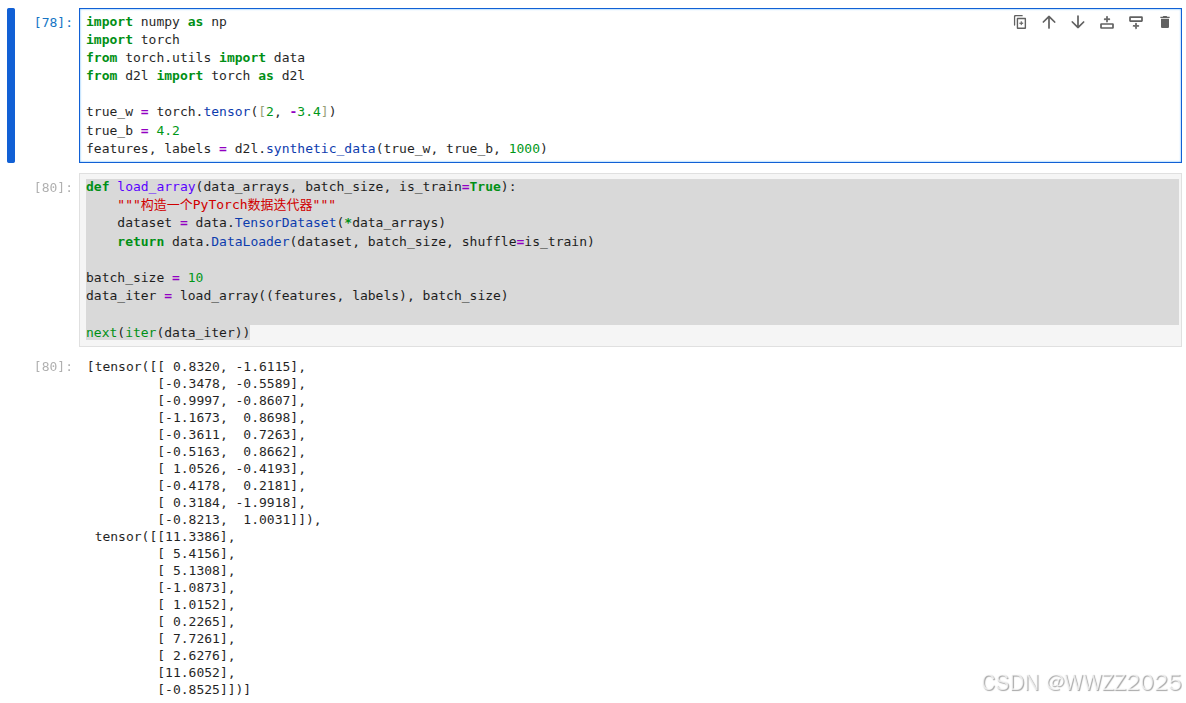
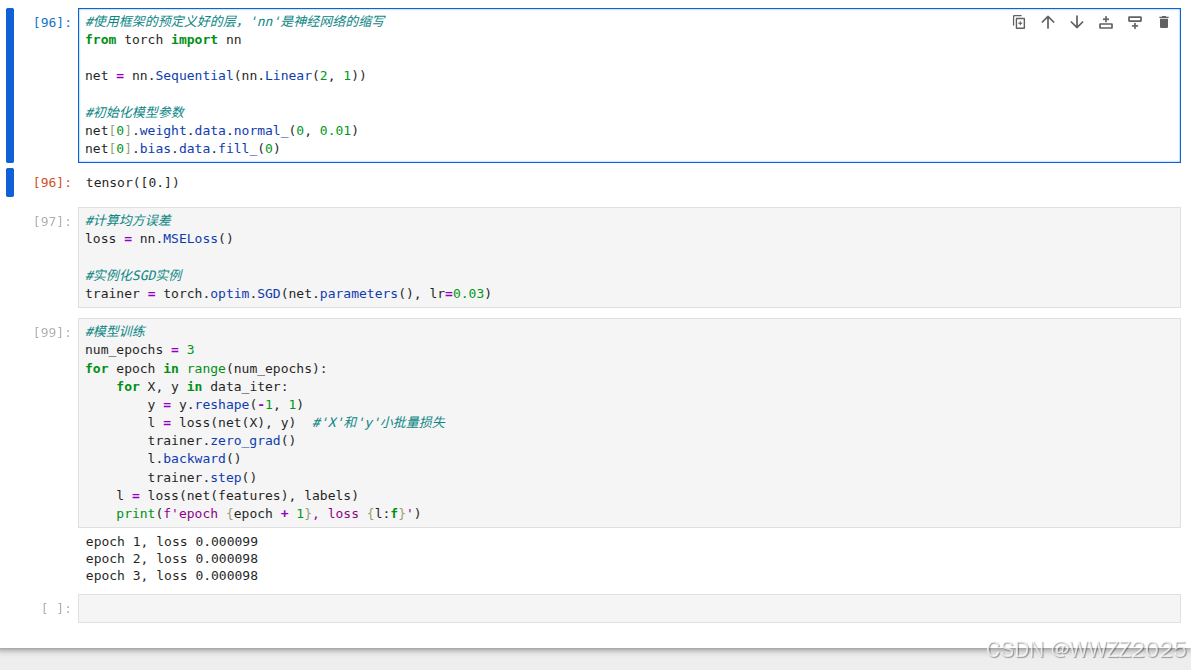
6.7 上述步骤的简洁实现

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2ltrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)def load_array(data_arrays, batch_size, is_train=True):"""构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features, labels), batch_size)next(iter(data_iter))#使用框架的预定义好的层，'nn'是神经网络的缩写
from torch import nnnet = nn.Sequential(nn,Linear(2, 1))#初始化模型参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)#计算均方误差
loss = nn.MSELoss()#实例化SGD实例
trainer = torch.optim.SGD(net.parameters(), lr=0.03)#模型训练
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X), y)  #'X'和'y'小批量损失trainer.zero_grad()l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')