【优先级队列（堆）】数据流的中位数（hard）

数据流的中位数（hard）

题⽬链接：295. 数据流的中位数

题⽬描述：

中位数是有序整数列表中的中间值。如果列表的⼤⼩是偶数，则没有中间值，中位数是两个中间值的平均值。
• 例如 arr = [2,3,4] 的中位数是 3 。
• 例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。
实现 MedianFinder 类:
• MedianFinder() 初始化 MedianFinder 对象。
• void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
• double findMedian() 返回到⽬前为⽌所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。
⽰例 1：
输⼊
[“MedianFinder”, “addNum”, “addNum”, “findMedian”, “addNum”, “findMedian”]
[[], [1], [2], [], [3], []]
输出
[null, null, null, 1.5, null, 2.0]
解释
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = [1]
medianFinder.addNum(2); // arr = [1, 2]
medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2)
medianFinder.addNum(3); // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0
提⽰:
-10⁵ <= num <= 10⁵
在调⽤ findMedian 之前，数据结构中⾄少有⼀个元素
最多 5 * 10⁴次调⽤ addNum 和 findMedian

解法（利⽤两个堆）：

算法思路：

这是⼀道关于「堆」这种数据结构的⼀个「经典应⽤」。
我们可以将整个数组「按照⼤⼩」平分成两部分（如果不能平分，那就让较⼩部分的元素多⼀个），较⼩的部分称为左侧部分，较⼤的部分称为右侧部分：
• 将左侧部分放⼊「⼤根堆」中，然后将右侧元素放⼊「⼩根堆」中；
• 这样就能在 O(1) 的时间内拿到中间的⼀个数或者两个数，进⽽求的平均数。
如下图所⽰：

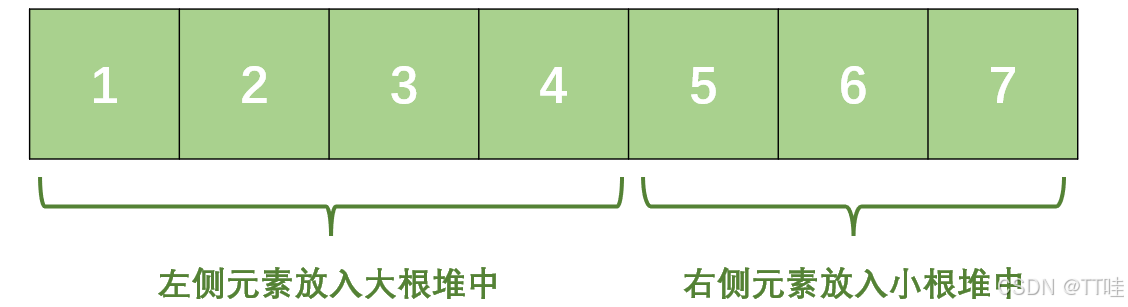
于是问题就变成了「如何将⼀个⼀个从数据流中过来的数据，动态调整到⼤根堆或者⼩根堆中，并且保证两个堆的元素⼀致，或者左侧堆的元素⽐右侧堆的元素多⼀个」
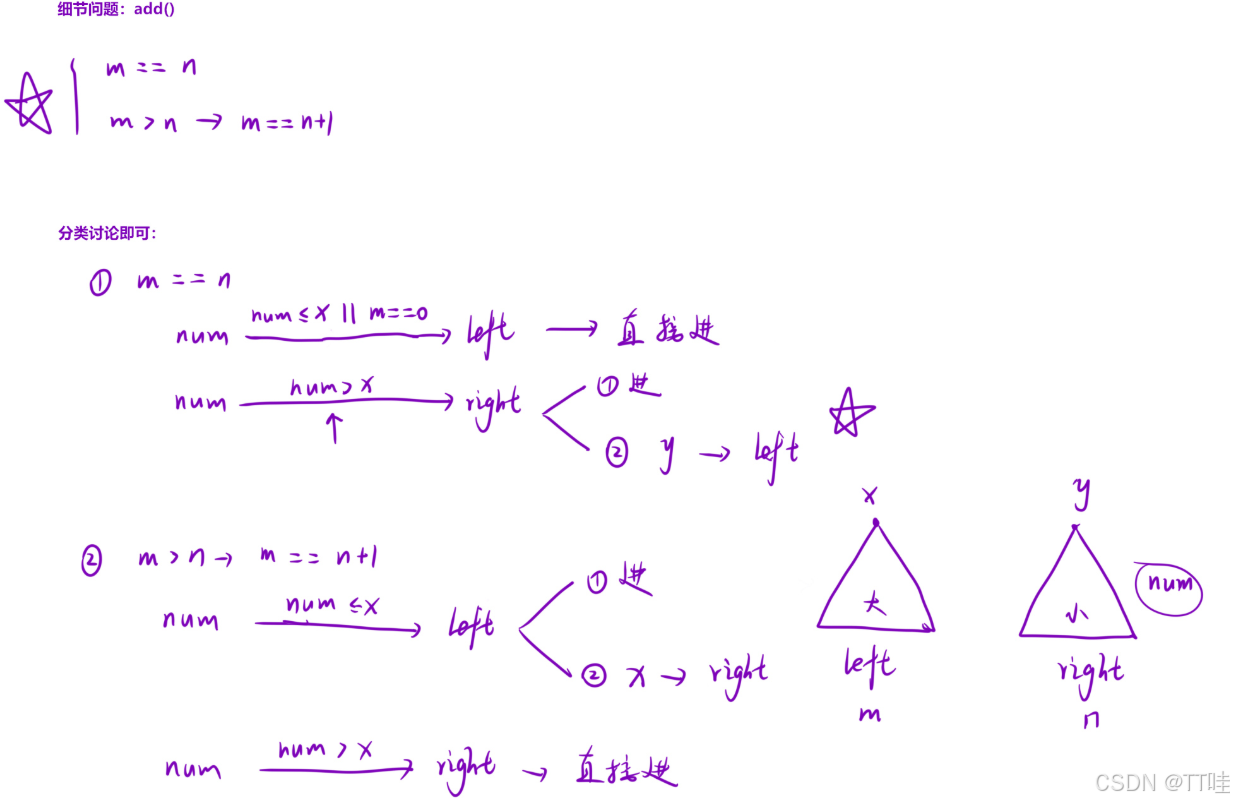
为了⽅便叙述，将左侧的「⼤根堆」记为 left ，右侧的「⼩根堆」记为 right ，数据流中来的「数据」记为 x 。
其实，就是⼀个「分类讨论」的过程：

1. 如果左右堆的「数量相同」， left.size() == right.size() ：
   a. 如果两个堆都是空的，直接将数据 x 放⼊到 left 中；
   b. 如果两个堆⾮空：
   i. 如果元素要放⼊左侧，也就是 x <= left.top() ：那就直接放，因为不会影响我们制定的规则；
   ii. 如果要放⼊右侧
   • 可以先将 x 放⼊ right 中，
   • 然后把 right 的堆顶元素放⼊ left 中 ；
2. 如果左右堆的数量「不相同」，那就是 left.size() > right.size() ：
   a. 这个时候我们关⼼的是 x 是否会放⼊ left 中，导致 left 变得过多：
   i. 如果 x 放⼊ right 中，也就是 x >= right.top() ，直接放；
   ii. 反之，就是需要放⼊ left 中：
   • 可以先将 x 放⼊ left 中，
   • 然后把 left 的堆顶元素放⼊ right 中 ；
   只要每⼀个新来的元素按照「上述规则」执⾏，就能保证 left 中放着整个数组排序后的「左半部分」， right 中放着整个数组排序后的「右半部分」，就能在 O(1) 的时间内求出平均数。

算法代码:

class MedianFinder
{PriorityQueue<Integer> left;PriorityQueue<Integer> right;public MedianFinder() {left = new PriorityQueue<Integer>((a, b) -> b - a); // ⼤根堆right = new PriorityQueue<Integer>((a, b) -> a - b); // ⼩根堆}public void addNum(int num) {// 分情况讨论if(left.size() == right.size()){if(left.isEmpty() || num <= left.peek()){left.offer(num);}else{right.offer(num);left.offer(right.poll());}}else{if(num <= left.peek()){left.offer(num);right.offer(left.poll());}else{right.offer(num);}}}public double findMedian() {if(left.size() == right.size()) return (left.peek() + right.peek()) / 2.0;else return left.peek();}
}