当前位置：首页 > news >正文

VMD分解+核主成分降维+物理信息神经网络！VMD-KPCA-PINN多变量时序光伏功率预测，MATLAB代码

news 2025/10/28 10:29:51

代码实现了一个基于变分模态分解（VMD）、核主成分分析（KPCA）和物理信息神经网络（PINN）的组合预测模型，用于对北半球光伏发电数据进行时间序列预测。以下是详细分析：

一、主要功能
该代码实现了一个多阶段混合预测模型，包括：

VMD分解：将原始光伏特征数据分解为多个分量（IMF）和一个残差项。
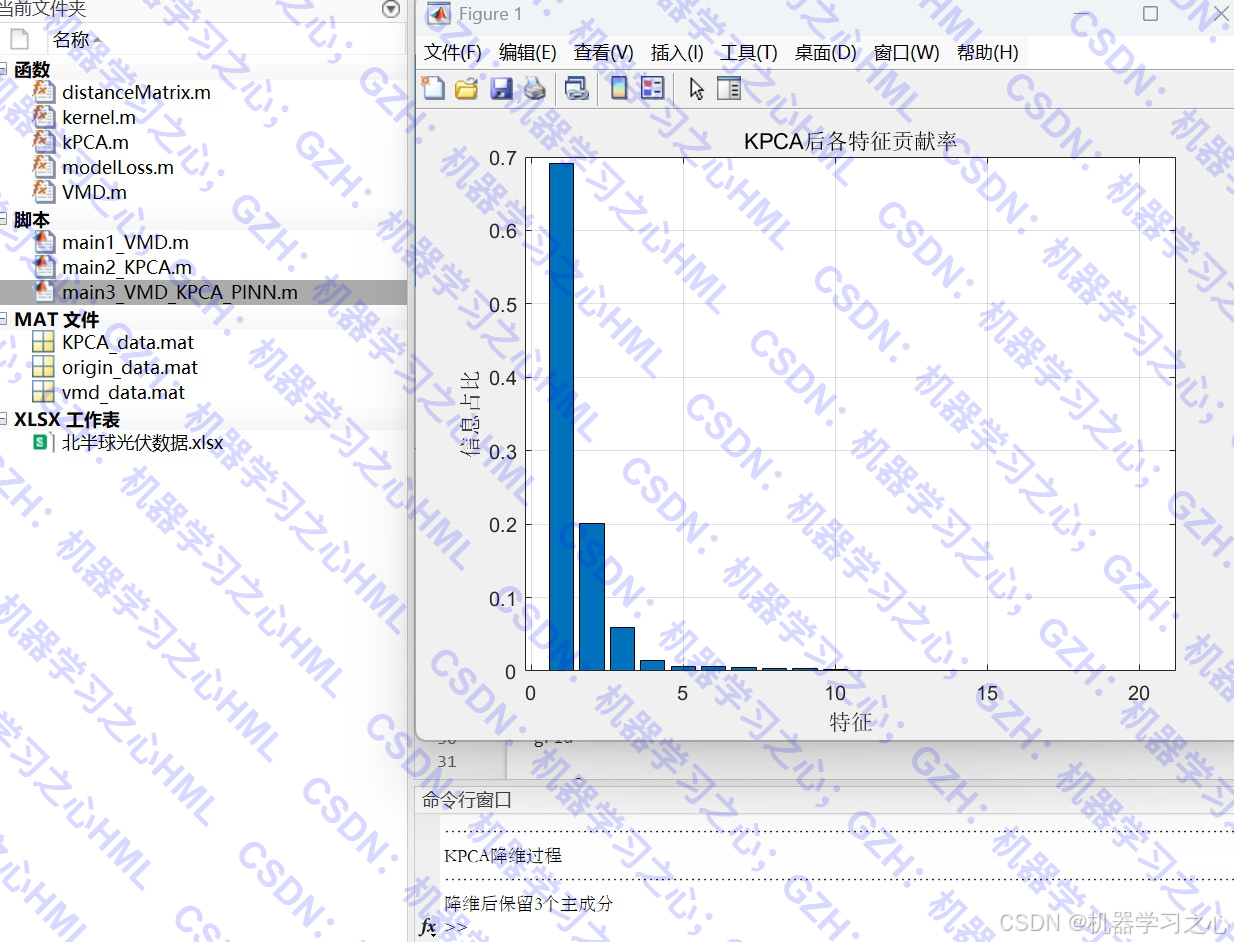
KPCA降维：对IMF进行核主成分分析，提取主要特征。
PINN预测：使用物理信息神经网络对降维后的数据进行训练和预测，引入物理约束提升泛化能力。
二、算法步骤
VMD分解（main1_VMD.m）：
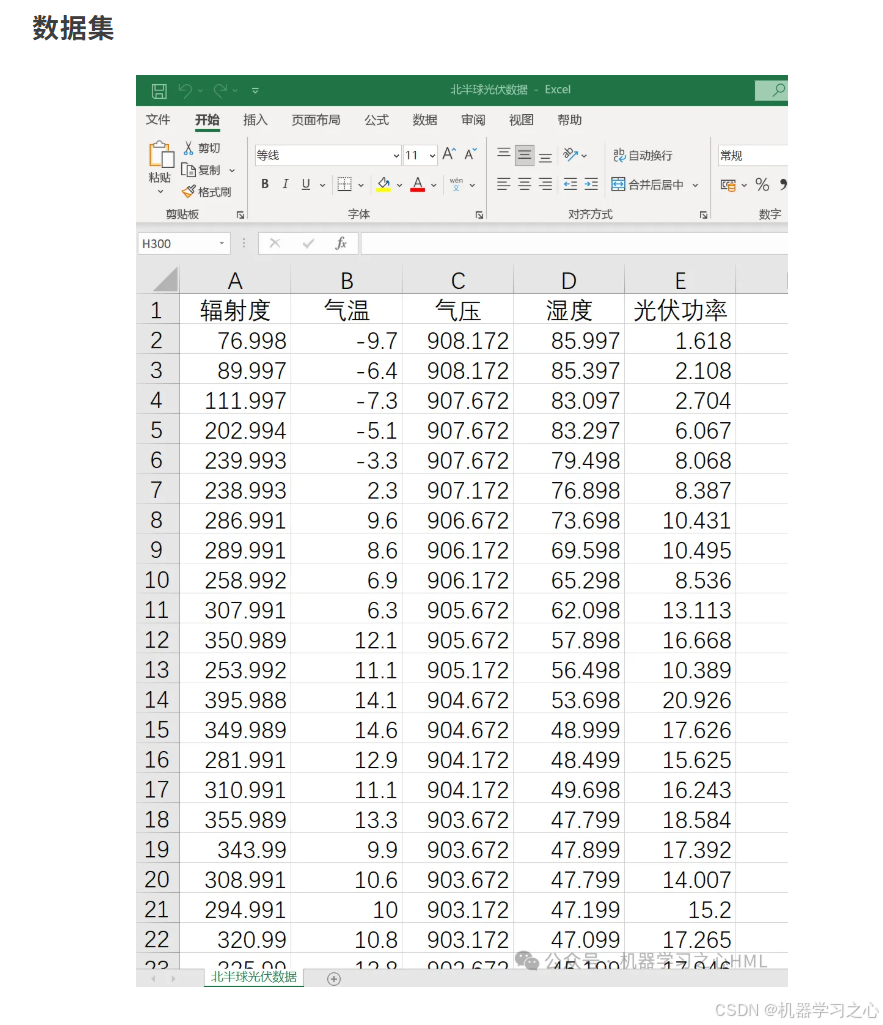
• 读取光伏数据（4个特征 + 1个输出）。
• 对每个特征进行VMD分解，得到多个IMF和残差。
• 可视化分解结果并保存。
KPCA降维（main2_KPCA.m）：
• 加载VMD分解后的IMF数据。
• 使用多项式核函数进行KPCA。
• 保留累计贡献率 >90% 的主成分。
PINN预测（main3_VMD_KPCA_PINN.m）：
• 重构数据集：将历史数据作为输入，未来数据作为输出。
• 划分训练集和测试集。
• 数据归一化。
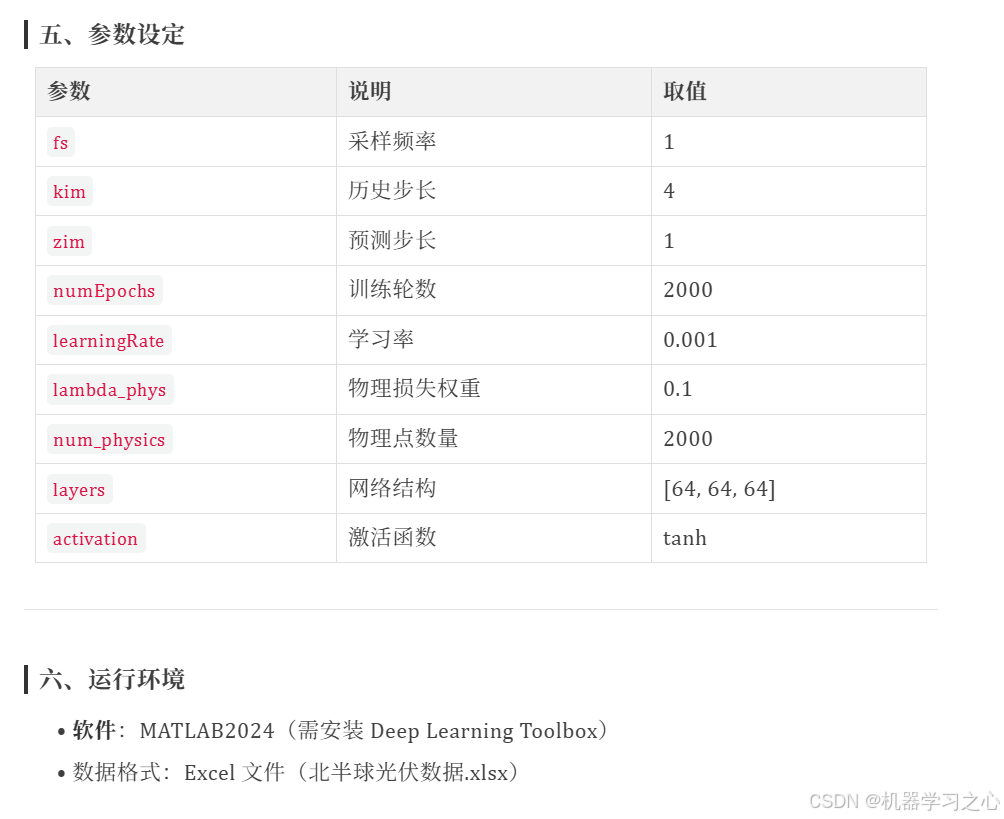
• 构建PINN网络结构（3个隐藏层，64神经元，tanh激活）。
• 引入物理点计算物理残差损失。
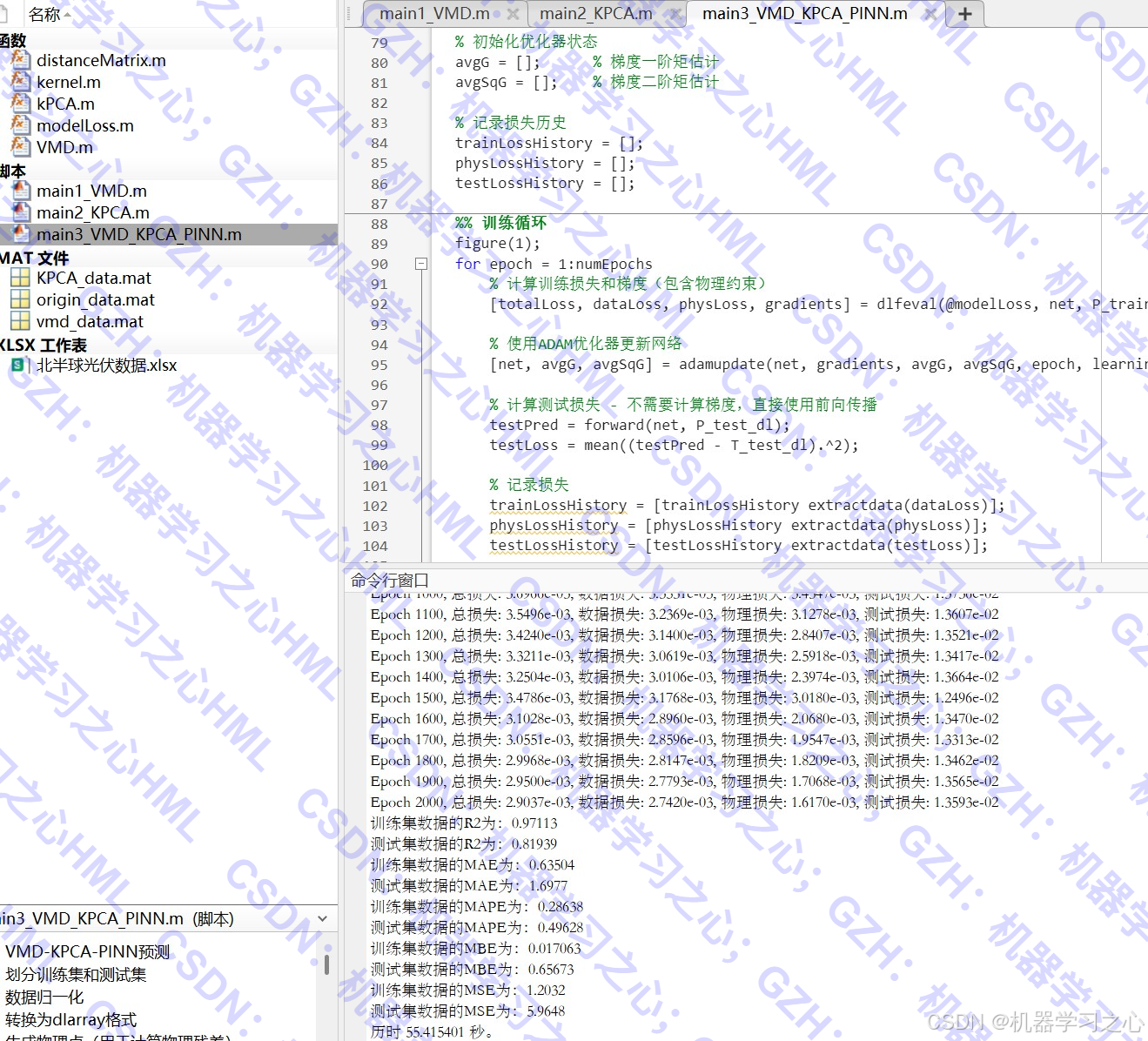
• 使用Adam优化器训练网络。
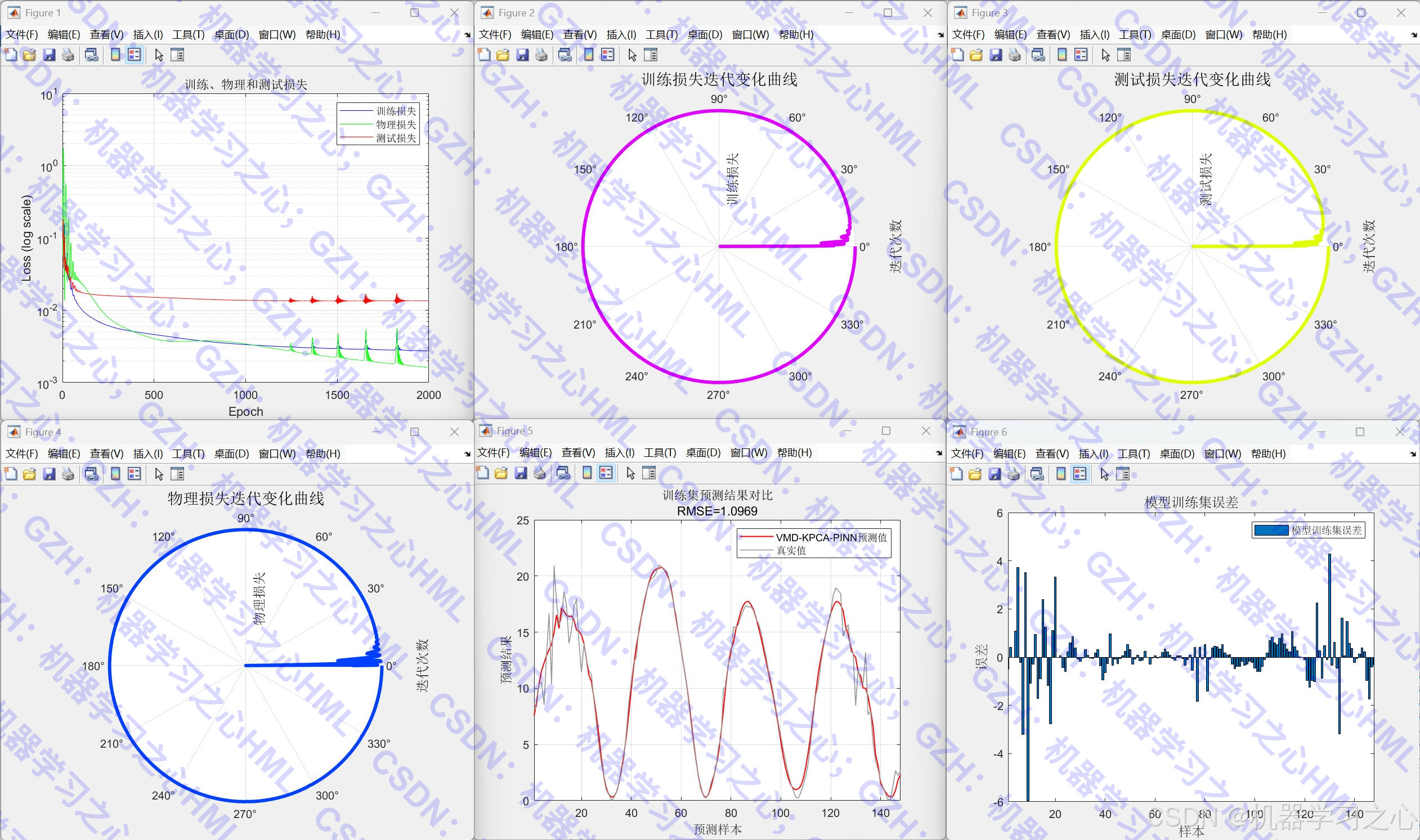
• 反归一化并评估预测结果（RMSE, R², MAE, MAPE, MBE, MSE）。
• 绘制损失曲线、预测对比图、误差图、拟合图等。
三、技术路线
原始数据 → VMD分解 → IMFs → KPCA降维 → 特征选择 → 数据重构 → PINN训练与预测 → 结果评估
四、公式原理

在这里插入图片描述

完整代码私信回复VMD分解+核主成分降维+物理信息神经网络！VMD-KPCA-PINN多变量时序光伏功率预测，MATLAB代码

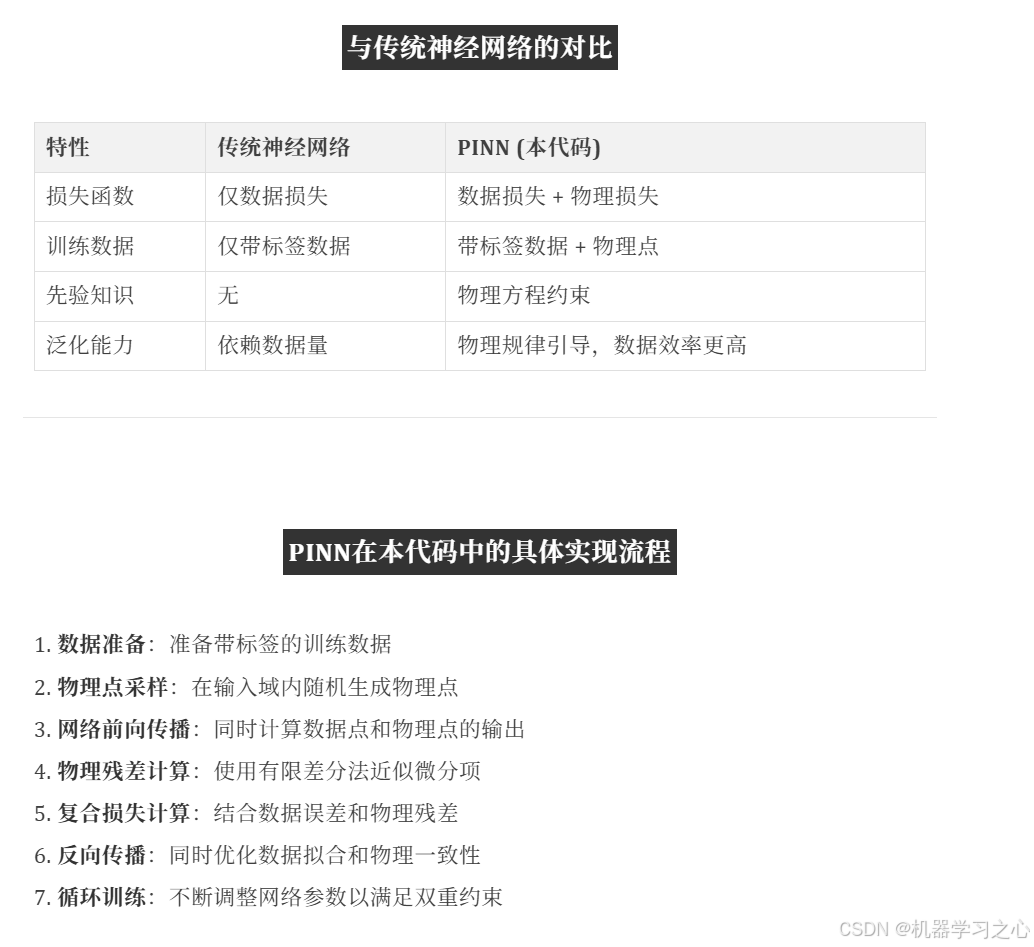
PINN 核心特征在代码中的体现

物理约束的引入 (modelLoss.m)
% 使用有限差分法近似计算导数

% 定义物理方程残差（以常微分方程 du/dt + u = 0 为例）

% 计算物理损失
体现了PINN的核心：不仅拟合数据，还强制网络满足物理规律（微分方程）。

复合损失函数 (modelLoss.m)
% 组合总损失 = 数据损失 + λ * 物理损失
PINN的标志性特征——将物理知识作为正则化项加入损失函数。
物理点生成 (main.m)
% 生成物理点（用于计算物理残差）
num_physics = 1000;
X_physics = rand(f_, num_physics);
PINN需要在物理域内采样点来评估物理残差，这些点不需要有标签数据。
物理损失权重 (main.m)
lambda_phys = 0.1; % 物理损失项的权重
通过超参数λ平衡数据拟合与物理约束的重要性。
训练过程中同时优化两种损失 (main.m)
% 计算包含物理约束的损失和梯度
[totalLoss, dataLoss, physLoss, gradients] = dlfeval(@modelLoss, net, P_train_dl, T_train_dl, X_physics_dl, lambda_phys);
在每次训练迭代中同时考虑数据误差和物理一致性。

在这里插入图片描述
核心思想
代码完整实现了PINN的核心思想：

• ✅ 引入了物理方程作为软约束
• ✅ 使用复合损失函数平衡数据拟合和物理一致性
• ✅ 在无标签的物理点上评估物理残差
• ✅ 通过超参数控制物理约束的强度
• ✅ 同时优化数据误差和物理残差
PINN与传统神经网络的根本区别——将物理先验知识 explicitly 嵌入到学习过程中，而不仅仅依赖数据驱动。

部分源码

.lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, “Courier New”, monospace; font-style: normal; font-weight: normal; }
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 导入数据
%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)‘;
T_train = res(1: num_train_s, f_ + 1: end)’;
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)‘;
T_test = res(num_train_s + 1: end, f_ + 1: end)’;
N = size(P_test, 2);
%% 数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax(‘apply’, P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax(‘apply’, T_test, ps_output);
%% 转换为dlarray格式
P_train_dl = dlarray(P_train, ‘CB’); % 特征在行，样本在列
T_train_dl = dlarray(t_train, ‘CB’);
P_test_dl = dlarray(P_test, ‘CB’);
T_test_dl = dlarray(t_test, ‘CB’);
%% 生成物理点（用于计算物理残差）
% 假设输入特征包含时间和空间信息，这里在[0,1]范围内随机生成物理点
num_physics = 1000; % 物理点数量
X_physics = rand(f_, num_physics); % 随机生成物理点
X_physics_dl = dlarray(X_physics, ‘CB’); % 转换为dlarray
%% 创建PINN模型
layers = [
featureInputLayer(f_, ‘Name’, ‘input’)
fullyConnectedLayer(64, ‘Name’, ‘fc1’)
往期回顾：