当前位置：首页 > news >正文

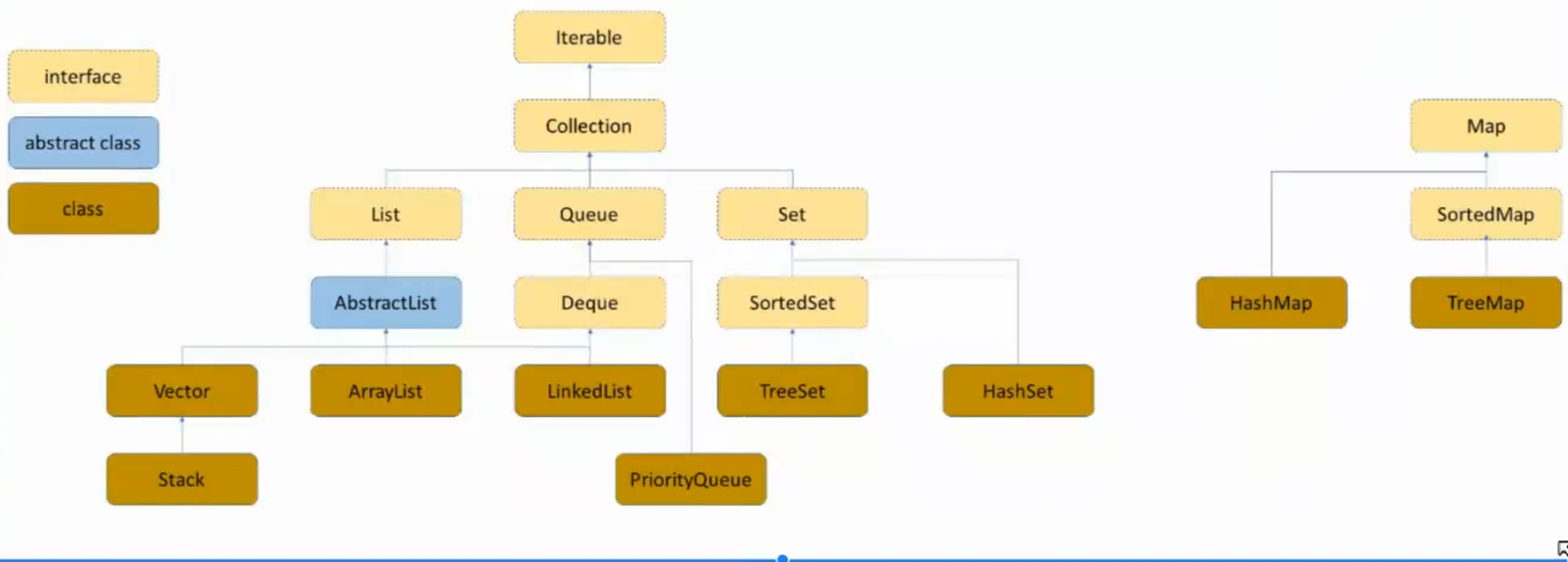
Map Set

news 2025/10/28 8:18:34

1、概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

它的左右子树也分别为二叉搜索树

2.二叉搜索的操作

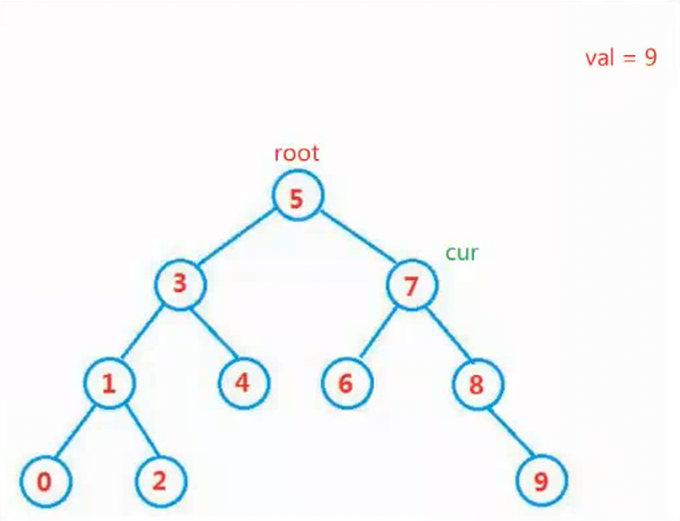
1.查找

边界处理：首先判断根节点是否为空，如果根节点为空，说明树中没有任何节点，直接返回false。
迭代查找：
- 从根节点开始，使用cur指针遍历树
- 比较当前节点cur的值与目标值val：
  - 若cur.val < val：目标值可能在右子树中，将cur移至右子节点
  - 若cur.val > val：目标值可能在左子树中，将cur移至左子节点
  - 若两者相等：找到目标值，返回true
查找结束：当cur指针变为null时，说明遍历完了所有可能的路径却没有找到目标值，返回false

  static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;public boolean search(int val) {if(root == null) {return false;}TreeNode cur = root;while (cur != null) {if(cur.val < val) {cur = cur.right;}else if(cur.val >val) {cur = cur.left;}else {return true;}}return false;}

2.插入

插入一个树的时候就是插入二叉搜索树的叶子节点,在标准的二叉搜索树（BST）插入逻辑中，新节点始终作为叶子节点插入

若插入到非叶子位置（如替换某个中间节点），会导致该节点原有左 / 右子树被迫 “移位”，极易打破 “左小右大” 的规则；
但是我们再刚刚的查找过程中，已经找到应该插入的这个点了，但是继续往下执行了，但是有不能回去了，也没有标记刚刚的节点，就比较麻烦

这时候就用到父亲节点 parent ，设置好 parent 标记好父亲节点

   public void insert(int val) {if(root == null) {root = new TreeNode(val);return;}TreeNode cur = root;TreeNode parent = null;while (cur != null) {if(cur.val < val) {parent = cur;cur = cur.right;}else if(cur.val > val) {parent = cur;cur = cur.left;}else {//一样的值 不进行存储return;}}TreeNode newNode = new TreeNode(val);if(parent.val > val) {parent.left = newNode;}else {parent.right = newNode;}}

新节点始终作为叶子节点添加到树中，通过遍历找到 “应该属于新节点的父节点”，直接将新节点挂在父节点的左 / 右子树位置。这种方式不会修改任何已有节点的值，仅通过调整指针关系就能维持 BST 性质，是 BST 插入的标准实现。

3.删除

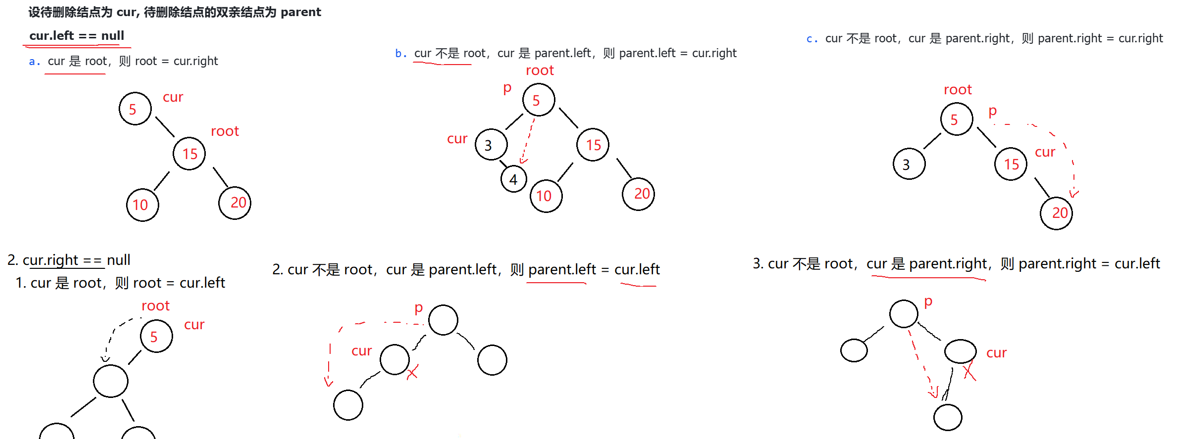
设待删除结点为cur,待删除结点的双亲结点为parent

1. cur.left == null

a. cur是root，则root=cur.right

b. cur不是root，cur是parent.left，则parent.left=cur.right

c. cur不是root，cur是parent.right，则parent.right=cur.right

2. cur.right==null

a. cur是root，则root=cur.left

b. cur不是root，cur是parent.left，则parent.left=cur.left

c. cur不是root，cur是parent.right，则parent.right=cur.left

3. cur.left!=null&&cur.right!=null

a.需要使用替换法继进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题

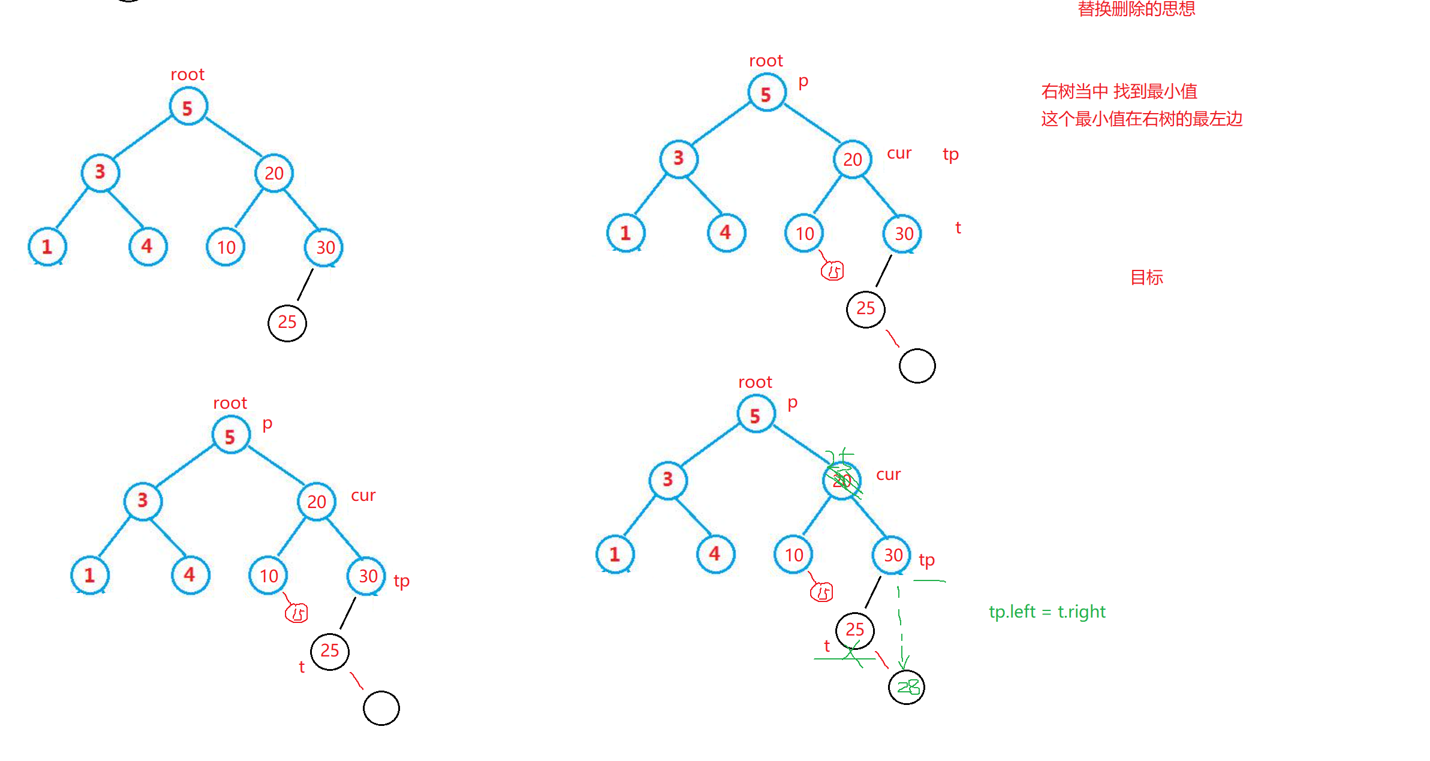
加入说删除的点是20 ，cur = 20，怎么办才能把20 节点给干掉，主要就是谁要往20 这个节点放，放10？n那10 的右边要是有呢，假如说10 的右边是15，先假设一下，那也就是说5 的右节点直接等于10，那10 的右边的数据15往哪里放呢，或者说30放哪里，所以说就很麻烦

用替换思想，删除这个删除节点的左节点的右节点（因为比删除节点的左节点大，比删除节点的右边小）或者删除这个删除节点的右节点的左节点（因为比删除节点的右节点小，比删除节点的左节点大）

但是如果25左右两边都还有节点那就不能放到这，同理15也是，那就是25的左边，就是找删除节点右边最小的如果一直还有节点的前提下，其实就是右树的最左边

注意右树下面不会有比他还小的数了，所以最多只会有一个右树，此时这时候要删除右树最小的数

同理，删除要删除的节点左边的这个树，要找它的最大值的节点，也就是这个替换的这个节点，顶多也就是有一个左节点

其实就是又成上面哪两种情况了

  public void remove(int val) {TreeNode cur = root;TreeNode parent = null;while (cur != null) {if(cur.val < val) {parent = cur;cur = cur.right;}else if(cur.val > val) {parent = cur;cur = cur.left;}else {//开始删除了removeNode(cur,parent);return;}}}/*** 删除节点* @param cur 要删除的节点* @param parent 要删除的节点的父亲节点*/private void removeNode(TreeNode cur, TreeNode parent) {if(cur.left == null) {if(cur == root) {root = cur.right;}else if(cur == parent.left) {parent.left = cur.right;}else {parent.right = cur.right;}}else if(cur.right == null) {if(cur == root) {root = cur.left;}else if(cur == parent.left) {parent.left = cur.left;}else {parent.right = cur.left;}}else {TreeNode target = cur.right;TreeNode targetParent = cur;while (target.left != null) {targetParent = target;target = target.left;}//开始替换值cur.val = target.val;}}

那如果是这样子的图，我们的代码就是有一个小的bug了

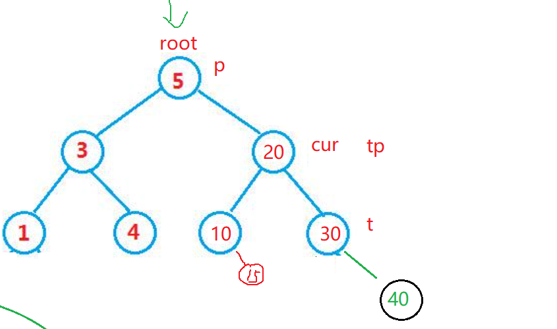
二叉搜索树的删除策略是：用cur的中序后继节点（或前驱节点）的值替换cur的值，然后删除这个后继节点。（中序后继：在中序遍历中紧跟cur的节点，对 BST 而言，是cur右子树中值最小的节点，即右子树的最左节点）

1. `cur.val = target.val`：值的替换

target是前面逻辑中找到的 “中序后继节点”（cur右子树的最左节点，值最小）。
这行代码的作用是：将cur的值替换为target的值。相当于 “间接删除”cur—— 因为cur的原始值已经被移除（被target的值覆盖），而target的位置更容易删除（因为target是最左节点，必然没有左子树，最多只有右子树）。

2. 后续删除`target`的逻辑：调整树结构

由于target是cur右子树的最左节点，它的左子树一定为null（否则会继续向左遍历），因此target只有两种可能：

没有子节点（叶子节点）；
只有右子节点（target.right可能为null或一个子树）。

因此，删除target只需将其右子树 “接” 到它的父节点targetParent上即可，具体分两种情况：

若target是targetParent的右子节点（target == targetParent.right）：说明target是targetParent直接的右孩子（比如cur的右子树本身就是最左节点，即target = cur.right，此时targetParent = cur）。此时只需让targetParent的右指针指向target的右子树（targetParent.right = target.right），即可跳过target，完成删除。
若target是targetParent的左子节点（else 分支）：说明target是targetParent的左孩子（即target在cur的右子树中更深处，经过多次向左遍历才找到）。此时只需让targetParent的左指针指向target的右子树（targetParent.left = target.right），即可跳过target，完成删除。

  public void remove(int val) {TreeNode cur = root;TreeNode parent = null;while (cur != null) {if(cur.val < val) {parent = cur;cur = cur.right;}else if(cur.val > val) {parent = cur;cur = cur.left;}else {//开始删除了removeNode(cur,parent);return;}}}/*** 删除节点* @param cur 要删除的节点* @param parent 要删除的节点的父亲节点*/private void removeNode(TreeNode cur, TreeNode parent) {if(cur.left == null) {if(cur == root) {root = cur.right;}else if(cur == parent.left) {parent.left = cur.right;}else {parent.right = cur.right;}}else if(cur.right == null) {if(cur == root) {root = cur.left;}else if(cur == parent.left) {parent.left = cur.left;}else {parent.right = cur.left;}}else {TreeNode target = cur.right;TreeNode targetParent = cur;while (target.left != null) {targetParent = target;target = target.left;}//开始替换值cur.val = target.val;//删除if(target == targetParent.right) {targetParent.right = target.right;}else {targetParent.left = target.right;}}}

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。

对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。

但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：

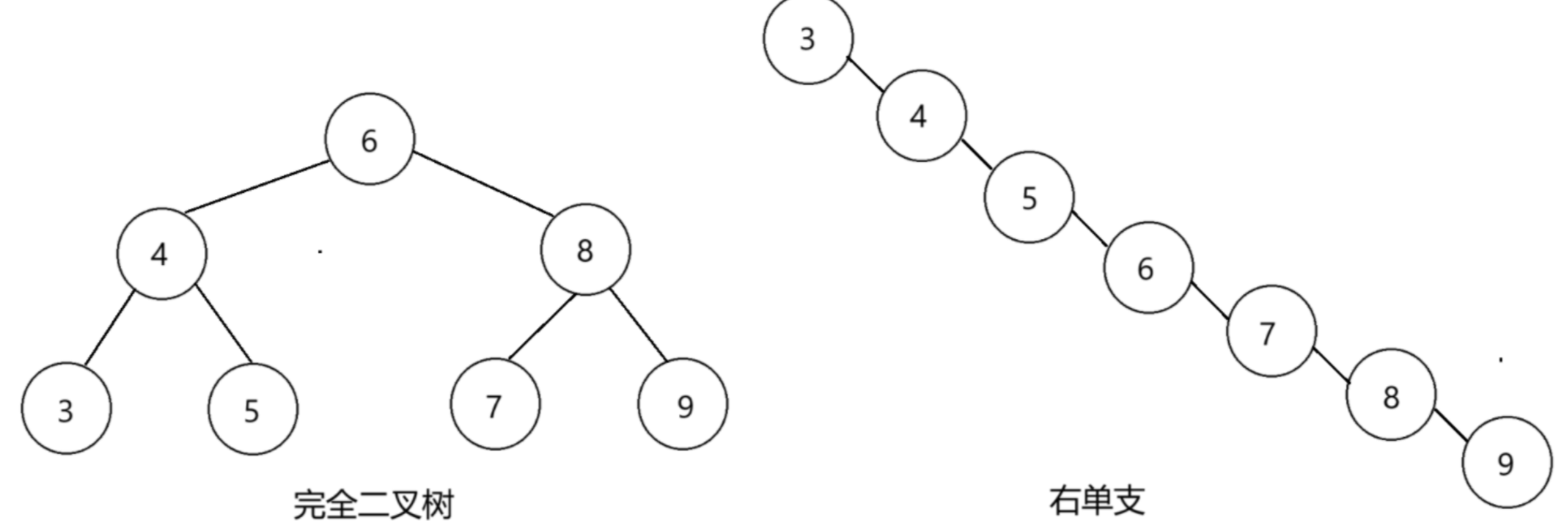
最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：logN

最差情况下，二叉搜索树退化为单支树，其平均比较次数为：n/2

问题：如果退化成单支树，二叉搜索树的性能就失去了。那能否进行改进，不论按照什么次序插入关键码，都可以是二叉搜索树的性能最佳？

7、和 java 类集的关系
TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set；实际上用的是红黑树，而红黑树是一棵近似平衡的二叉搜索树，即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证，关于红黑树的内容后序再进行讲解。（这些就可以解决上面的问题！！！）

二、搜索
1、概念及场景
Map和set是一种专门用来进行搜索的容器或者数据结构，其搜索的效率与其具体的实例化子类有关。以前常见的搜索方式有：

（1）直接遍历，时间复杂度为O(N)，元素如果比较多效率会非常慢

（2）二分查找，时间复杂度为,但搜索前必须要求序列是有序的

上述排序比较适合静态类型的查找，即一般不会对区间进行插入和删除操作了，而现实中的查找比如：

（1）根据姓名查询考试成绩

（2）通讯录，即根据姓名查询联系方式

（3）不重复集合，即需要先搜索关键字是否已经在集合中

可能在查找时进行一些插入和删除的操作，即动态查找，那上述两种方式就不太适合了，本节介绍的Map和Set是一种适合动态查找的集合容器。

2、模型
一般把搜索的数据称为关键字（Key），和关键字对应的称为值（Value），将其称之为Key-value的键值对，所以模型会有两种：

key（键）像 “大名”，是唯一标识；value（值）像 “小名”，是与这个唯一标识绑定的数据。

Map 中 key 必须唯一（重复 put 相同 key 会覆盖原有 value），就像每个人的 “大名” 在特定场景下唯一；但 value 可以重复（多个不同 key 能对应相同 value），比如 “张三” 和 “李四” 的小名可能都是 “小三”，这和现实中 “小名重复” 的情况一致。

（1）纯 key 模型，比如：

有一个英文词典，快速查找一个单词是否在词典中

快速查找某个名字在不在通讯录中

（2）Key-Value 模型，比如：

统计文件中每个单词出现的次数，统计结果是每个单词都有与其对应的次数：<单词，单词出现的次数>

梁山好汉的江湖绰号：每个好汉都有自己的江湖绰号

而Map中存储的就是key-value的键值对，Set中只存储了Key。

三、Map 的使用

Map 的官方文档：

https://docs.oracle.com/javase/8/docs/api/java/util/Map.html

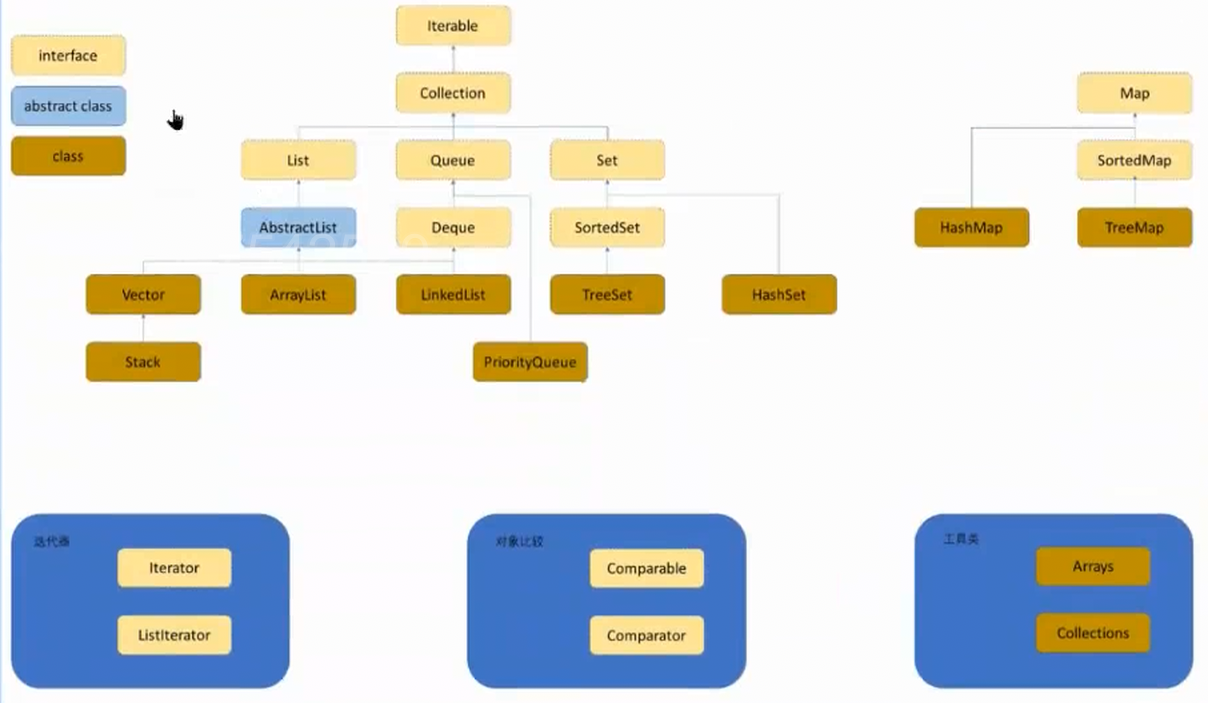
1、关于Map的说明

Map是一个接口类，该类没有继承自Collection，该类中存储的是结构的键值对，并且K一定是唯一的，不能重复。

映射（Map） 是一种键值对（Key-Value Pair）的集合，用于建立 “键” 到 “值” 的关联关系。

2、关于Map.Entry<K,V>的说明

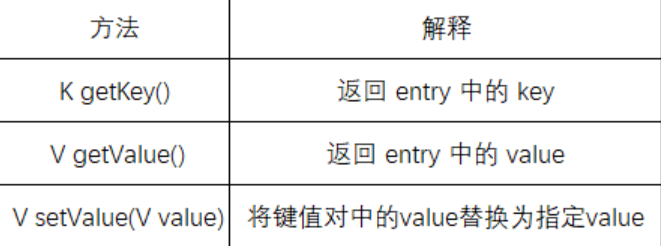
Map.Entry<K,V> 是Map内部实现的用来存放键值对映射关系的内部类，该内部类中主要提供了的获取，value的设置以及Key的比较方式。

1. 作为 `Map.Entry<K, V>` 接口的实现：

它是 Java 集合框架中键值对（Key-Value Pair）的载体，核心作用是封装 Map 中的一组 “键 - 值” 映射关系。

提供 getKey()、getValue()、setValue() 等方法，用于访问和修改键值对（比如遍历 Map 时，每个 Entry 就是一个独立的键值对单元）。

2. 作为红黑树的节点（以 `TreeMap` 底层为例）：

在 TreeMap 的实现中，Entry<K, V> 同时承担了红黑树节点的角色，用于维护有序的键值对结构：

包含 key（键）、value（值），满足键值对的存储需求；
包含 left（左子节点）、right（右子节点）、parent（父节点），构成二叉树的节点关系；
包含 color（颜色标记），这是红黑树的核心属性（用于自平衡调整，保证树的高度均匀）。

 Set<Map.Entry<String, Integer>> entries = map.entrySet();for(Map.Entry<String, Integer> entry : entries) {String key = entry.getKey();Integer val = entry.getValue();System.out.println("key: "+key +" val: "+val);}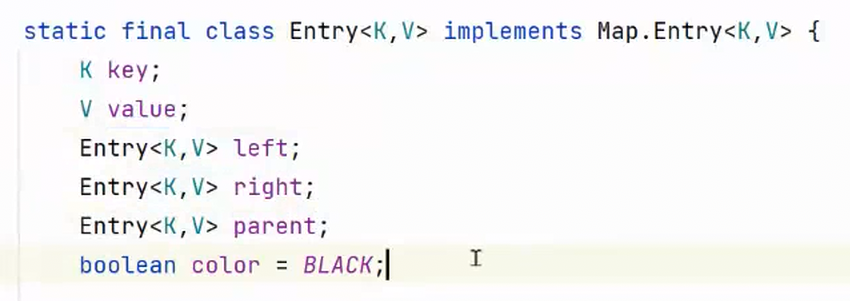

实现Map.Entry<K,V>：表明这是一个存储键值对（key和value）的节点，符合Map中键值对的封装需求（与TreeMap存储键值对的特性一致）。
红黑树节点的核心属性：
- left、right：左、右子节点引用，是二叉树的基本结构；
- parent：父节点引用，用于红黑树旋转、调整时快速定位父节点；
- color：节点颜色（boolean color = BLACK，默认黑色），这是红黑树的标志性属性（红黑树节点只有红、黑两种颜色，用于维持树的平衡）。

Map 本身存储的是一系列键值对，但 Map 接口的设计更偏向于 “通过键找值”（如 get(key)、put(key, value)）。而当需要遍历 Map 中的所有键值对时（比如用 map.entrySet() 遍历），就需要一个对象来单独表示每一组键值对，Map.Entry 正是这个角色。

注：Map.Entry<K,V>并没有提供设置Key的方法

3、Map 的常用方法说明

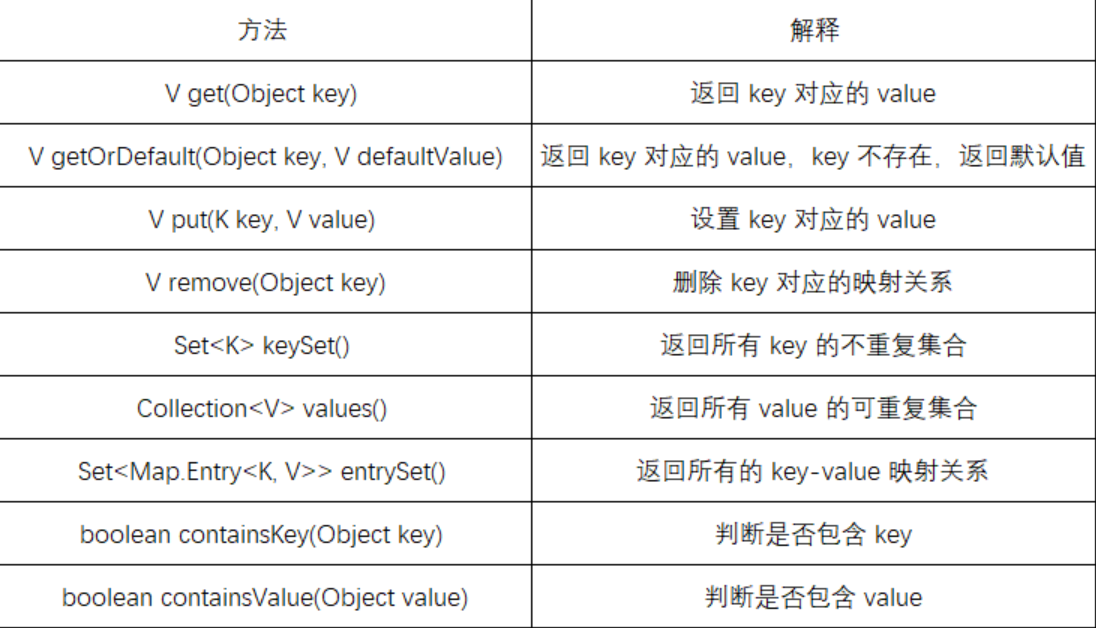
注:

（1）Map是一个接口，不能直接实例化对象，如果要实例化对象只能实例化其实现类TreeMap或者HashMap

（2）Map中存放键值对的Key是唯一的，value是可以重复的

（3）在TreeMap中插入键值对时，key不能为空，否则就会抛NullPointerException异常，value可以为空。但是HashMap的key和value都可以为空。

（4）Map中的Key可以全部分离出来，存储到Set中来进行访问(因为Key不能重复)。

（5）Map中的value可以全部分离出来，存储在Collection的任何一个子集合中(value可能有重复)。

（6）Map中键值对的Key不能直接修改，value可以修改，如果要修改key，只能先将该key删除掉，然后再来进行重新插入。

Set<Map.Entry<K,V>> entrySet 中Map.Entry<K,V>其实就是节点

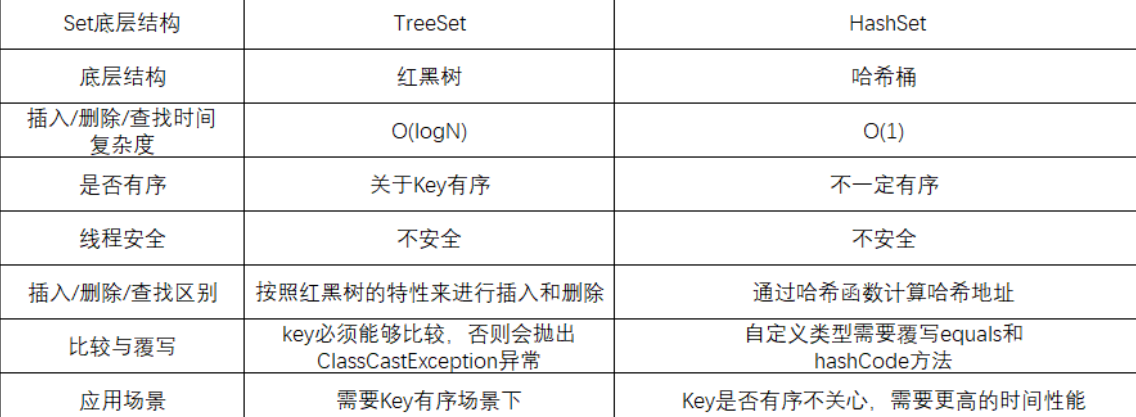
（7）TreeMap和HashMap的区别【HashMap我们在最后会讲到】

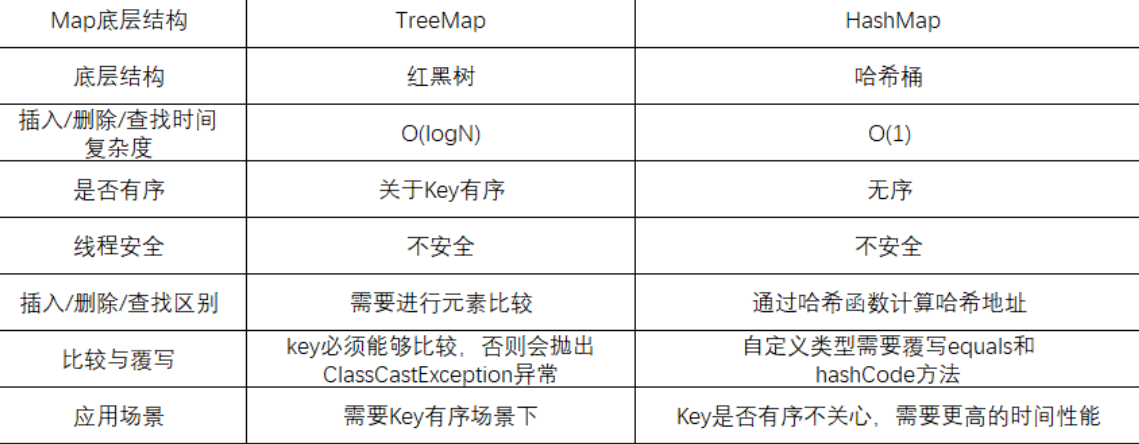
3.Map 的使用案例

import java.util.TreeMap;
import java.util.Map;public static void TestMap(){Map<String, String> m = new TreeMap<>();// put(key, value):插入key-value的键值对// 如果key不存在，会将key-value的键值对插入到map中,返回nullm.put("林冲", "豹子头");m.put("鲁智深", "花和尚");m.put("武松", "行者");m.put("宋江", "及时雨");String str = m.put("李逵", "黑旋风");System.out.println(m.size());System.out.println(m);// put(key,value): 注意key不能为空，但是value可以为空// key如果为空，会抛出空指针异常//m.put(null, "花名");str = m.put("无名", null);System.out.println(m.size());// put(key, value):// 如果key存在，会使用value替换原来key所对应的value，返回旧valuestr = m.put("李逵", "铁牛");// get(key): 返回key所对应的value// 如果key存在，返回key所对应的value// 如果key不存在，返回nullSystem.out.println(m.get("鲁智深"));System.out.println(m.get("史进"));//GetOrDefault(): 如果key存在，返回与key所对应的value，如果key不存在，返回一个默认值System.out.println(m.getOrDefault("李逵", "铁牛"));System.out.println(m.getOrDefault("史进", "九纹龙"));System.out.println(m.size());//containKey(key)：检测key是否包含在Map中，时间复杂度：O(logN)// 按照红黑树的性质来进行查找// 找到返回true，否则返回falseSystem.out.println(m.containsKey("林冲"));System.out.println(m.containsKey("史进"));// containValue(value): 检测value是否包含在Map中，时间复杂度: O(N)// 找到返回true，否则返回falseSystem.out.println(m.containsValue("豹子头"));System.out.println(m.containsValue("九纹龙"));// 打印所有的key// keySet是将map中的key防止在Set中返回的for(String s : m.keySet()){System.out.print(s + " ");}System.out.println();// 打印所有的value// values()是将map中的value放在collect的一个集合中返回的for(String s : m.values()){System.out.print(s + " ");}System.out.println();// 打印所有的键值对// entrySet(): 将Map中的键值对放在Set中返回了for(Map.Entry<String, String> entry : m.entrySet()){System.out.println(entry.getKey() + "--->" + entry.getValue());}System.out.println();
}

二、Set 的说明

Set 的官方文档https://docs.oracle.com/javase/8/docs/api/java/util/Set.html Set与Map主要的不同有两点：Set是继承自Collection的接口类，Set中只存储了Key。

在 Java 集合框架中，Set 是一个接口，它继承自Collection接口，用于存储不允许重复的元素，且不保证元素的顺序（部分实现类如TreeSet除外）。

核心特性

元素唯一性：Set中不会存储重复的元素（判断重复的依据是元素的equals()方法和hashCode()方法，若自定义类需重写这两个方法以保证逻辑正确）。
无索引：Set没有像List那样的索引机制，因此无法通过下标访问元素。
部分实现有序：
- HashSet：无序（基于哈希表实现）。
- LinkedHashSet：保持元素的插入顺序（基于哈希表 + 链表实现）。
- TreeSet：按元素的自然顺序或自定义比较器顺序排列（基于红黑树实现）。

1、常见方法说明

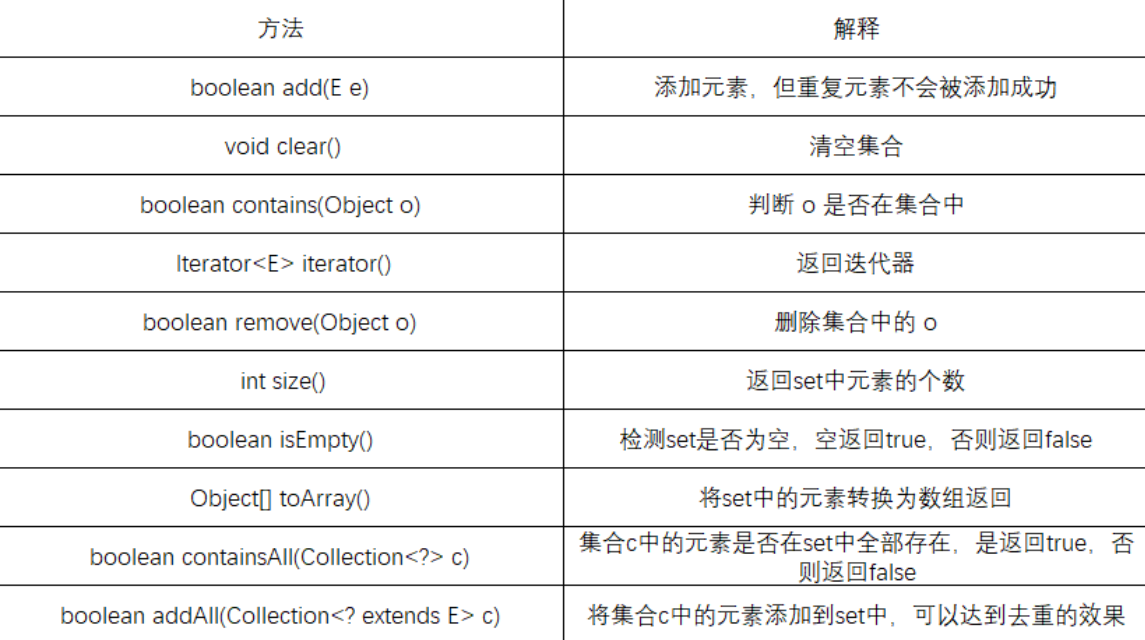
 public static void main2(String[] args) {Set<String> set = new TreeSet<>();set.add("abc");set.add("hello");set.add("ok");set.add("main");System.out.println(set);}

发现调用的是TreeSet

其实这个放到元素是放到TreeMap 里面，换句话说，我不管再Set里add 什么元素，key 的值是指定的，value 都是默认的Object 对象

注：

（1）Set是继承自Collection的一个接口类

（2）Set中只存储了key，并且要求key一定要唯一

（3）TreeSet的底层是使用Map来实现的，其使用key与Object的一个默认对象作为键值对插入到Map中的

（4）Set最大的功能就是对集合中的元素进行去重

（5）实现Set接口的常用类有TreeSet和HashSet，还有一个LinkedHashSet，LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。

（6）Set中的Key不能修改，如果要修改，先将原来的删除掉，然后再重新插入

（7）TreeSet中不能插入null的key，HashSet可以。

（8）TreeSet和HashSet的区别【HashSet我们在后面最后会讲到】

Set 的使用案例

import java.util.TreeSet;
import java.util.Iterator;
import java.util.Set;public static void TestSet(){Set<String> s = new TreeSet<>();// add(key): 如果key不存在，则插入，返回ture// 如果key存在，返回falseboolean isIn = s.add("apple");s.add("orange");s.add("peach");s.add("banana");System.out.println(s.size());System.out.println(s);isIn = s.add("apple");// add(key): key如果是空，抛出空指针异常//s.add(null);// contains(key): 如果key存在，返回true，否则返回falseSystem.out.println(s.contains("apple"));System.out.println(s.contains("watermelen"));// remove(key): key存在，删除成功返回true//              key不存在，删除失败返回false//              key为空，抛出空指针异常s.remove("apple");System.out.println(s);s.remove("watermelen");System.out.println(s);Iterator<String> it = s.iterator();while(it.hasNext()){System.out.print(it.next() + " ");}System.out.println();
}

1、概念

2.二叉搜索的操作

1.查找

3.删除

1. cur.val = target.val：值的替换

2. 后续删除target的逻辑：调整树结构

三、Map 的使用

1、关于Map的说明

2、关于Map.Entry的说明

1. 作为 Map.Entry接口的实现：

2. 作为红黑树的节点（以 TreeMap 底层为例）：

3、Map 的常用方法说明