03-Machine-4-fft.py K230进行快速傅里叶变换、频率计算及幅值计算功能演示
fft.py 主要实现了K230进行快速傅里叶变换、频率计算及幅值计算功能演示。
K230 canMV的FFT 模块提供了一个 FFT 类,支持三个主要函数:run()、freq() 和 amplitude(),用于分别进行快速傅里叶变换、频率计算及幅值计算。
FFT(快速傅里叶变换)模块用于对输入的时域数据进行傅里叶变换,将其转换为频域数据并返回相应的频率幅值。通过 FFT 运算,可以有效地将时域信号转换为频域信号,便于分析信号的频率成分。换句话说,FFT 能告诉我们:
信号中有哪些频率
各个频率对应的强度(幅值)
res = FFT.run()
返回值
返回值 | 描述 |
|---|---|
| 返回一个包含频域数据的 |
res = FFT.freq(points, sample_rate)
参数
参数名称 | 描述 | 输入/输出 |
|---|---|---|
| 参与 FFT 运算的点数。 | 输入 |
| 数据采样率。 | 输入 |
返回值
返回值 | 描述 |
|---|---|
| 返回一个列表,包含运算后各频率点的频率值。 |
mp = FFT.amplitude(FFT_res)
参数
参数名称 | 描述 | 输入/输出 |
|---|---|---|
| 函数 | 输入 |
返回值
返回值 | 描述 |
|---|---|
| 返回一个列表,包含各个频率点的幅值。 |
FFT 广泛应用于:
音频频谱分析(如音乐可视化)
图像频率分析(如滤波)
通信系统(调制、解调)
振动分析、雷达信号处理
FFT(data, 64, 0x555):data: 输入信号数据64: FFT点数(与采样点数相同)0x555: 可能是硬件相关的配置参数或偏移量
演示程序的主要功能如下:
生成一个由5个不同频率和幅度的余弦波叠加而成的信号。
对这个信号进行FFT变换,得到频域表示。
计算频域中各频率点的幅度。
计算各频率点对应的实际频率。
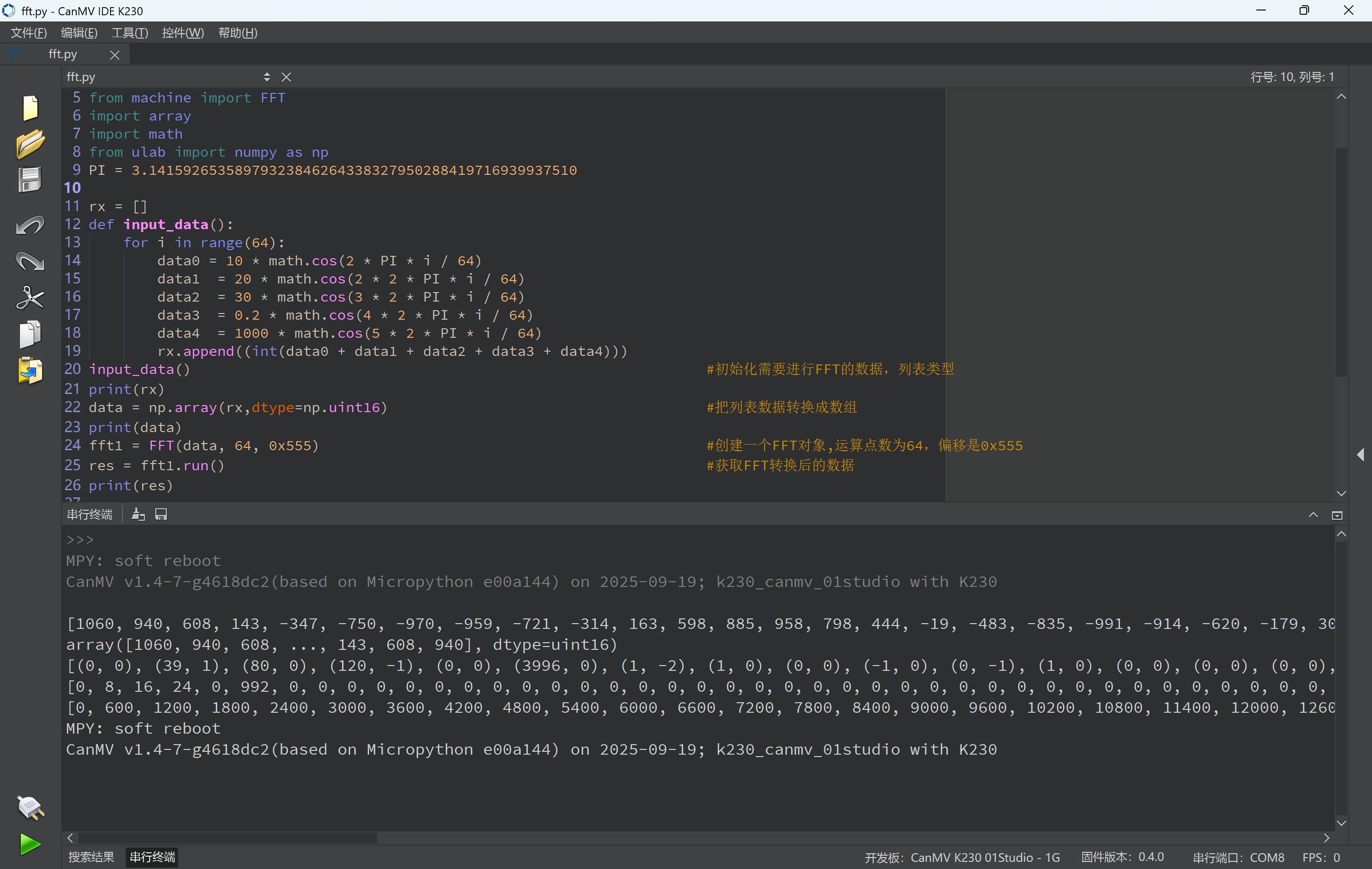
>>>
MPY: soft reboot
CanMV v1.4-7-g4618dc2(based on Micropython e00a144) on 2025-09-19; k230_canmv_01studio with K230[1060, 940, 608, 143, -347, -750, -970, -959, -721, -314, 163, 598, 885, 958, 798, 444, -19, -483, -835, -991, -914, -620, -179, 306, 721, 967, 985, 772, 376, -109, -571, -900, -1019, -900, -571, -109, 376, 772, 985, 967, 721, 306, -179, -620, -914, -991, -835, -483, -19, 444, 798, 958, 885, 598, 163, -314, -721, -959, -970, -750, -347, 143, 608, 940]
array([1060, 940, 608, ..., 143, 608, 940], dtype=uint16)
[(0, 0), (39, 1), (80, 0), (120, -1), (0, 0), (3996, 0), (1, -2), (1, 0), (0, 0), (-1, 0), (0, -1), (1, 0), (0, 0), (0, 0), (0, 0), (1, 0), (0, 0), (1, 0), (0, 0), (0, 0), (0, 0), (-1, 0), (0, 1), (-1, 0), (0, 0), (-1, 0), (-1, 0), (0, 0), (0, 0), (0, -1), (0, 0), (1, 1), (0, 0), (1, -1), (0, 0), (0, 1), (0, 0), (0, 0), (-1, 0), (-1, 0), (0, 0), (-1, 0), (0, -1), (-1, 0), (0, 0), (0, 0), (0, 0), (1, 0), (0, 0), (1, 0), (0, 0), (0, 0), (0, 0), (1, 0), (0, 1), (-1, 0), (0, 0), (1, 0), (1, 2), (3996, 0), (0, 0), (120, 1), (80, 0), (39, -1)]
[0, 8, 16, 24, 0, 992, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 992, 0, 24, 16, 8]
[0, 600, 1200, 1800, 2400, 3000, 3600, 4200, 4800, 5400, 6000, 6600, 7200, 7800, 8400, 9000, 9600, 10200, 10800, 11400, 12000, 12600, 13200, 13800, 14400, 15000, 15600, 16200, 16800, 17400, 18000, 18600, 19200, 19800, 20400, 21000, 21600, 22200, 22800, 23400, 24000, 24600, 25200, 25800, 26400, 27000, 27600, 28200, 28800, 29400, 30000, 30600, 31200, 31800, 32400, 33000, 33600, 34200, 34800, 35400, 36000, 36600, 37200, 37800]
MPY: soft reboot
CanMV v1.4-7-g4618dc2(based on Micropython e00a144) on 2025-09-19; k230_canmv_01studio with K230生成的信号成分:
| 成分 | 幅度 | 相对频率 | 说明 |
|---|---|---|---|
| data0 | 10 | 1×基频 | 主要成分 |
| data1 | 20 | 2×基频 | 二次谐波 |
| data2 | 30 | 3×基频 | 三次谐波 |
| data3 | 0.2 | 4×基频 | 微弱成分 |
| data4 | 1000 | 5×基频 | 强干扰信号 |
源代码如下:
# 基础示例
#
# 欢迎使用CanMV IDE, 点击IDE左下角的绿色按钮开始执行脚本from machine import FFT
import array
import math
from ulab import numpy as np
PI = 3.14159265358979323846264338327950288419716939937510rx = []
def input_data():for i in range(64):data0 = 10 * math.cos(2 * PI * i / 64)data1 = 20 * math.cos(2 * 2 * PI * i / 64)data2 = 30 * math.cos(3 * 2 * PI * i / 64)data3 = 0.2 * math.cos(4 * 2 * PI * i / 64)data4 = 1000 * math.cos(5 * 2 * PI * i / 64)rx.append((int(data0 + data1 + data2 + data3 + data4)))
input_data() #初始化需要进行FFT的数据,列表类型
print(rx)
data = np.array(rx,dtype=np.uint16) #把列表数据转换成数组
print(data)
fft1 = FFT(data, 64, 0x555) #创建一个FFT对象,运算点数为64,偏移是0x555
res = fft1.run() #获取FFT转换后的数据
print(res)res = fft1.amplitude(res) #获取各个频率点的幅值
print(res)res = fft1.freq(64,38400) #获取所有频率点的频率值
print(res)