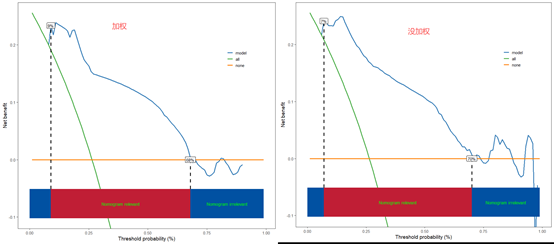
R语言绘制复杂加权数据(nhanes数据)生存分析决策曲线
决策曲线分析(Decision Curve Analysis, DCA)是一种用于评估、比较和优化诊断试验、预测模型或分子标志物临床实用性的统计方法。它由Andrew J. Vickers和Eugene B. Elkin于2006年提出,旨在弥补传统统计指标(如灵敏度、特异度、ROC曲线下面积)在评估模型临床价值方面的不足。

传统的统计指标主要关注模型的区分度(discrimination) 和 校准度(calibration),但它们无法直接回答一个关键的临床问题:“使用这个模型来指导临床决策,是否能为患者带来净收益(net benefit)?”
决策曲线分析的核心思想正是解决这个问题。它通过模拟在不同阈值概率(threshold probability) 下做出临床决策的过程,来量化模型的临床净收益。
在既往文章,本人介绍了我的ggscidca包,可以用于逻辑回归,生存分析等各种决策曲线绘制,但是据我所知,目前还没有R包能支持复杂加权数据(nhanes数据)生存分析决策曲线,因此本次升级了新版本的ggscidca包添加了nhanes数据生存分析决策曲线功能
下面我来演示一下,使用我自己提取的一个nhanes数据
好的,废话不多说,先导入数据和R包
library(survey)
library(ggscidca)
library(scinhanes)
bc<-read.csv("E:/r/test/nahnesme.csv",sep=',',header=TRUE)
bc <- na.omit(bc)
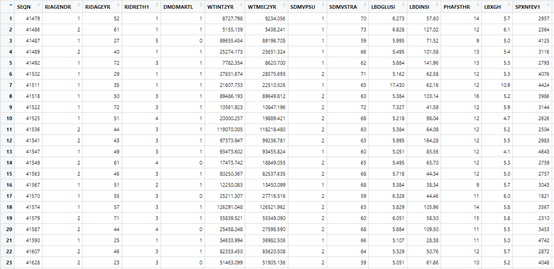
我介绍一下数据,SEQN:序列号,RIAGENDR, # 性别, RIDAGEYR, # 年龄,RIDRETH1, # 种族,DMDMARTL, # 婚姻状况,WTINT2YR,WTMEC2YR, # 权重,SDMVPSU, # psu,SDMVSTRA,# strata,LBDGLUSI, #血糖mmol表示,LBDINSI, #胰岛素( pmmol/L),PHAFSTHR #餐后血糖,LBXGH #糖化血红蛋白,SPXNFEV1, #FEV1:第一秒用力呼气量,SPXNFVC #FVC:用力肺活量,ml(估计肺容量),LBDGLTSI #餐后2小时血糖,factor.FVC是我把肺活量分为了2分类,方便用于测试。
把分类变量转成因子
bc$DMDMARTL<-ifelse(bc$DMDMARTL==1,1,0)
bc$RIAGENDR<-as.factor(bc$RIAGENDR)
bc$RIDRETH1<-as.factor(bc$RIDRETH1)
bc$DMDMARTL<-as.factor(bc$DMDMARTL)
bc$oGTT2<-as.factor(bc$oGTT2)
如果做预测模型要拆分成建模集和验证集。我这里拆分一下
set.seed(123)
tr1<- sample(nrow(bc),0.7*nrow(bc))##随机无放抽取
bc_train <- bc[tr1,]#70%数据集
bc_test<- bc[-tr1,]#30%数据集
建立抽样调查函数
bcSvy2<- svydesign(ids = ~ SDMVPSU, strata = ~ SDMVSTRA, weights = ~ WTMEC2YR,nest=TRUE,data = bc_train)
建立生存分析模型
svyfit <- svycoxph(Surv(time, factor.FVC) ~ RIDAGEYR+RIAGENDR+LBDINSI+RIDRETH1, x = TRUE,design = bcSvy2)
绘制复杂加权数据(nhanes数据)决策曲线一共需要2步:
1. 第一步,把模型变成ggscidca包能够识别的类型
fit<-scisvycoxphmodel(svyfit,username=username,token=token)
2. 绘制决策曲线
scidca(fit)
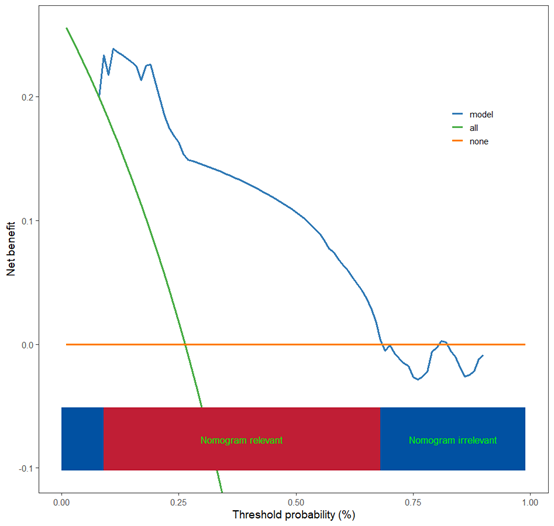
还可以修饰一下
scidca(fit,threshold.text=T,threshold.line=T)
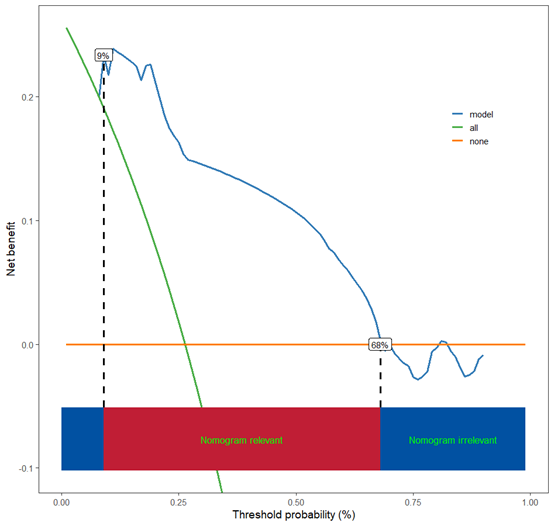
如果咱们想看验证集的决策曲线
fit<-scisvycoxphmodel(svyfit,newdata =bc_test,username=username,token=token)
scidca(fit,newdata =bc_test)
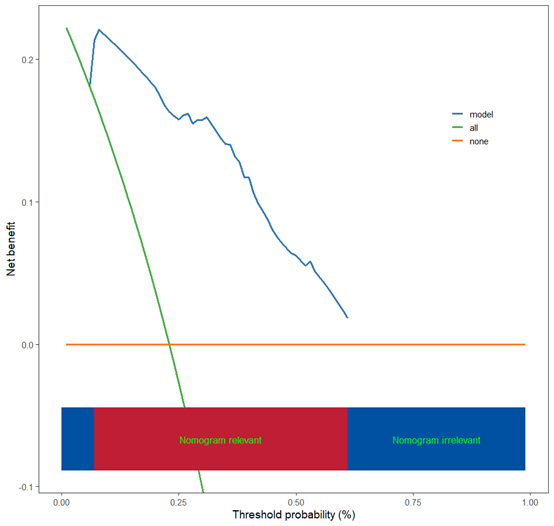
这样就轻松放入把验证集的决策曲线也做出来了,如果咱们按照普通方法来做nhanes的加权cox回归决策曲线看看
#####普通做法
f1<-coxph(Surv(time, factor.FVC) ~ RIDAGEYR+RIAGENDR+LBDINSI+RIDRETH1,bc_train)
scidca(f1,threshold.text=T,threshold.line=T)
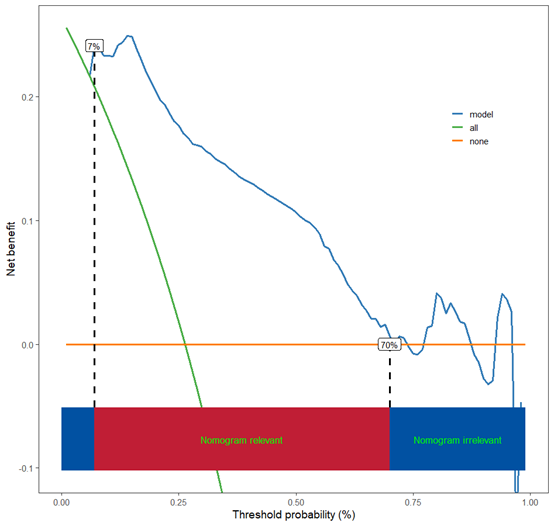
咱们可以看到,加权的和普通的不加权决策曲线无论是阈值还是图形都是有区别的