「用Python来学微积分」17. 导数与导函数
导数不仅是微积分的核心概念,更是描述变化率的有力工具。本文将带你从几何直观和物理意义的角度,深入理解导数与导函数的概念体系。
一、函数在一点的导数:变化率的精确刻画
1.1 导数的定义与数学表达
导数的概念源于对瞬时变化率的精确描述。设函数 y=f(x)y=f(x)y=f(x) 在点 x0x_0x0 的某个邻域内有定义,当自变量 xxx 在 x0x_0x0 处有增量 ΔxΔxΔx(且 x0+Δxx_0+Δxx0+Δx 仍在该邻域内),函数相应取得增量 Δy=f(x0+Δx)−f(x0)Δy=f(x_0+Δx)-f(x_0)Δy=f(x0+Δx)−f(x0)。
导数定义:如果极限 limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δx\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0) 存在,则称函数 y=f(x)y=f(x)y=f(x) 在点 x0x_0x0 处可导,并称该极限值为函数在点 x0x_0x0 处的导数,记作 f′(x0)f'(x_0)f′(x0),或 dydx∣x=x0\frac{dy}{dx}|_{x=x_0}dxdy∣x=x0 或 df(x)dx∣x=x0\frac{df(x)}{dx}|_{x=x_0}dxdf(x)∣x=x0。
1.2 导数的物理意义:从平均变化率到瞬时变化率
导数的本质是平均变化率在自变量增量趋于零时的极限,即瞬时变化率。这一概念在物理学中有广泛应用:
- 瞬时速度:物体位移 s(t)s(t)s(t) 对时间 ttt 的导数表示瞬时速度 v(t)=s′(t)v(t)=s'(t)v(t)=s′(t)
- 瞬时加速度:速度 v(t)v(t)v(t) 对时间 ttt 的导数表示瞬时加速度 a(t)=v′(t)a(t)=v'(t)a(t)=v′(t)
- 线密度:细杆质量 m(l)m(l)m(l) 对长度 lll 的导数表示线密度 ρ(l)=m′(l)ρ(l)=m'(l)ρ(l)=m′(l)
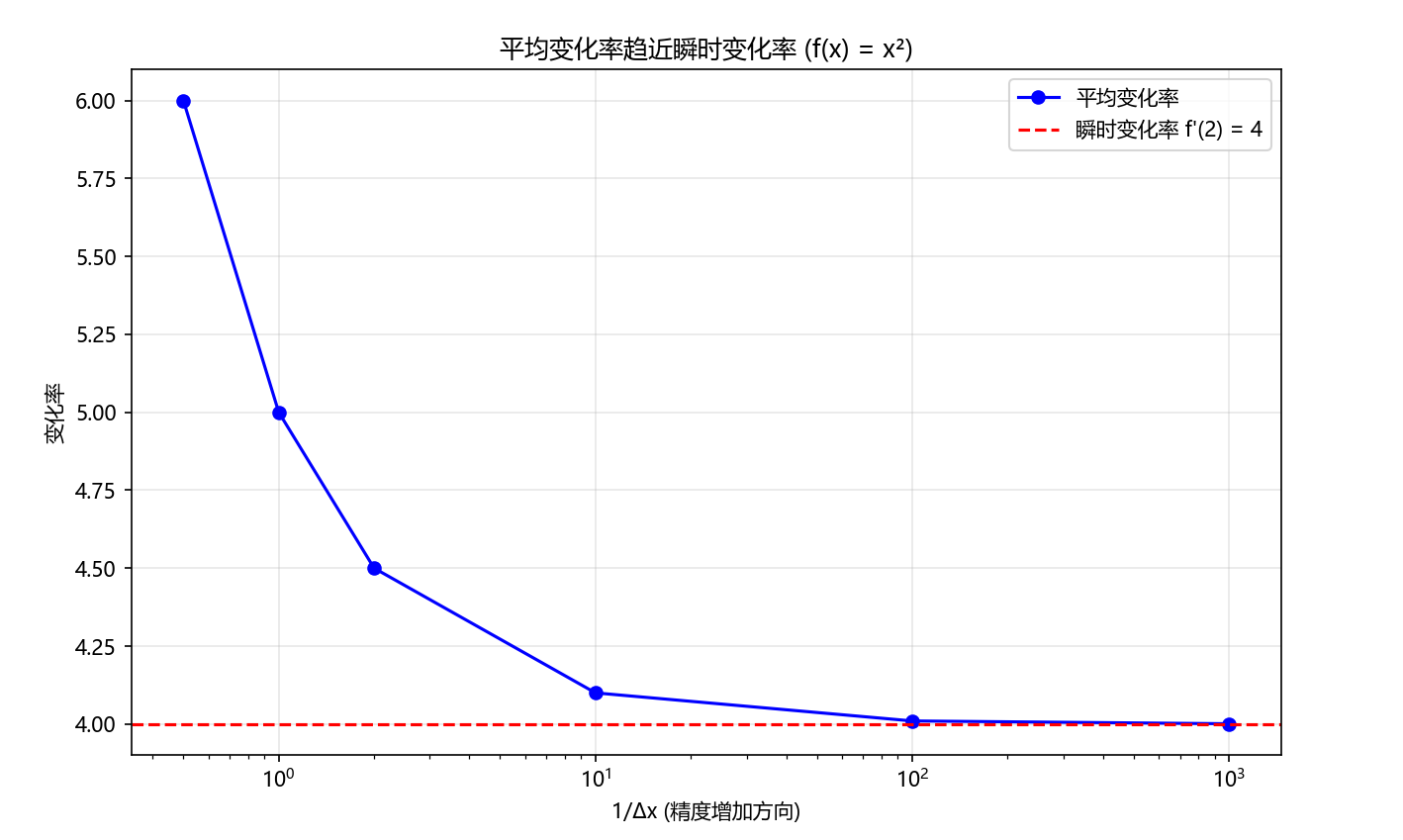
Python可视化:平均变化率趋近瞬时变化率
import matplotlib.pyplot as plt
import numpy as npdef demonstrate_instantaneous_rate():"""演示平均变化率如何趋近瞬时变化率"""# 定义函数:f(x) = x^2f = lambda x: x**2x0 = 2exact_derivative = 4 # f'(x) = 2x, f'(2)=4# 不同的Δx值delta_x_values = [2.0, 1.0, 0.5, 0.1, 0.01, 0.001]average_rates = []for dx in delta_x_values:average_rate = (f(x0 + dx) - f(x0)) / dxaverage_rates.append(average_rate)error = abs(average_rate - exact_derivative)print(f"Δx = {dx:.4f}, 平均变化率 = {average_rate:.4f}, 误差 = {error:.4f}")# 可视化plt.figure(figsize=(10, 6))plt.plot([1/dx for dx in delta_x_values], average_rates, 'bo-', label='平均变化率')plt.axhline(y=exact_derivative, color='r', linestyle='--', label=f'瞬时变化率 f\'({x0}) = {exact_derivative}')plt.xlabel('1/Δx (精度增加方向)')plt.ylabel('变化率')plt.title('平均变化率趋近瞬时变化率 (f(x) = x²)')plt.legend()plt.grid(True, alpha=0.3)plt.xscale('log')plt.show()demonstrate_instantaneous_rate()
运行结果:
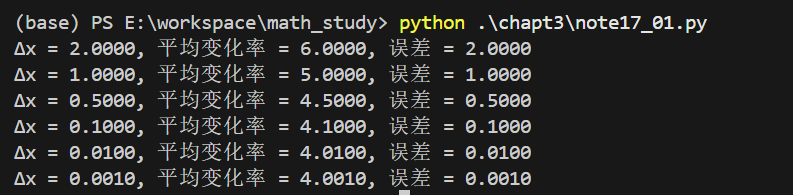
二、函数在一点的单侧导数:处理特殊点的利器
2.1 单侧导数的定义
对于定义在闭区间或分段函数,我们需要引入单侧导数的概念:
- 右导数:函数 f(x)f(x)f(x) 在点 x0x_0x0 处的右导数定义为 f+′(x0)=limΔx→0+f(x0+Δx)−f(x0)Δxf'_+(x_0) = \lim_{\Delta x \to 0^+} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}f+′(x0)=Δx→0+limΔxf(x0+Δx)−f(x0)
- 左导数:函数 f(x)f(x)f(x) 在点 x0x_0x0 处的左导数定义为 f−′(x0)=limΔx→0−f(x0+Δx)−f(x0)Δxf'_-(x_0) = \lim_{\Delta x \to 0^-} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}f−′(x0)=Δx→0−limΔxf(x0+Δx)−f(x0)
其中 Δx→0+\Delta x \to 0^+Δx→0+ 表示 Δx\Delta xΔx 从正方向趋于0,Δx→0−\Delta x \to 0^-Δx→0− 表示 Δx\Delta xΔx 从负方向趋于0。
2.2 可导的充要条件
函数 f(x)f(x)f(x) 在点 x0x_0x0 处可导的充分必要条件是:左导数 f−′(x0)f'_-(x_0)f−′(x0) 和右导数 f+′(x0)f'_+(x_0)f+′(x0) 都存在且相等。
当左右导数存在但不相等时,函数在该点不可导,图像在该点会出现"尖点"。
2.3 典型应用:绝对值函数的可导性分析
经典例子:函数 f(x)=∣x∣f(x)=|x|f(x)=∣x∣ 在 x=0x=0x=0 处的可导性
- 右导数:f+′(0)=limΔx→0+∣Δx∣−0Δx=limΔx→0+ΔxΔx=1f'_+(0) = \lim_{\Delta x \to 0^+} \frac{|\Delta x|-0}{\Delta x} = \lim_{\Delta x \to 0^+} \frac{\Delta x}{\Delta x} = 1f+′(0)=limΔx→0+Δx∣Δx∣−0=limΔx→0+ΔxΔx=1
- 左导数:f−′(0)=limΔx→0−∣Δx∣−0Δx=limΔx→0−−ΔxΔx=−1f'_-(0) = \lim_{\Delta x \to 0^-} \frac{|\Delta x|-0}{\Delta x} = \lim_{\Delta x \to 0^-} \frac{-\Delta x}{\Delta x} = -1f−′(0)=limΔx→0−Δx∣Δx∣−0=limΔx→0−Δx−Δx=−1
由于左导数 (−1)(-1)(−1) 不等于右导数 (1)(1)(1),所以 f(x)=∣x∣f(x)=|x|f(x)=∣x∣ 在 x=0x=0x=0 处不可导。
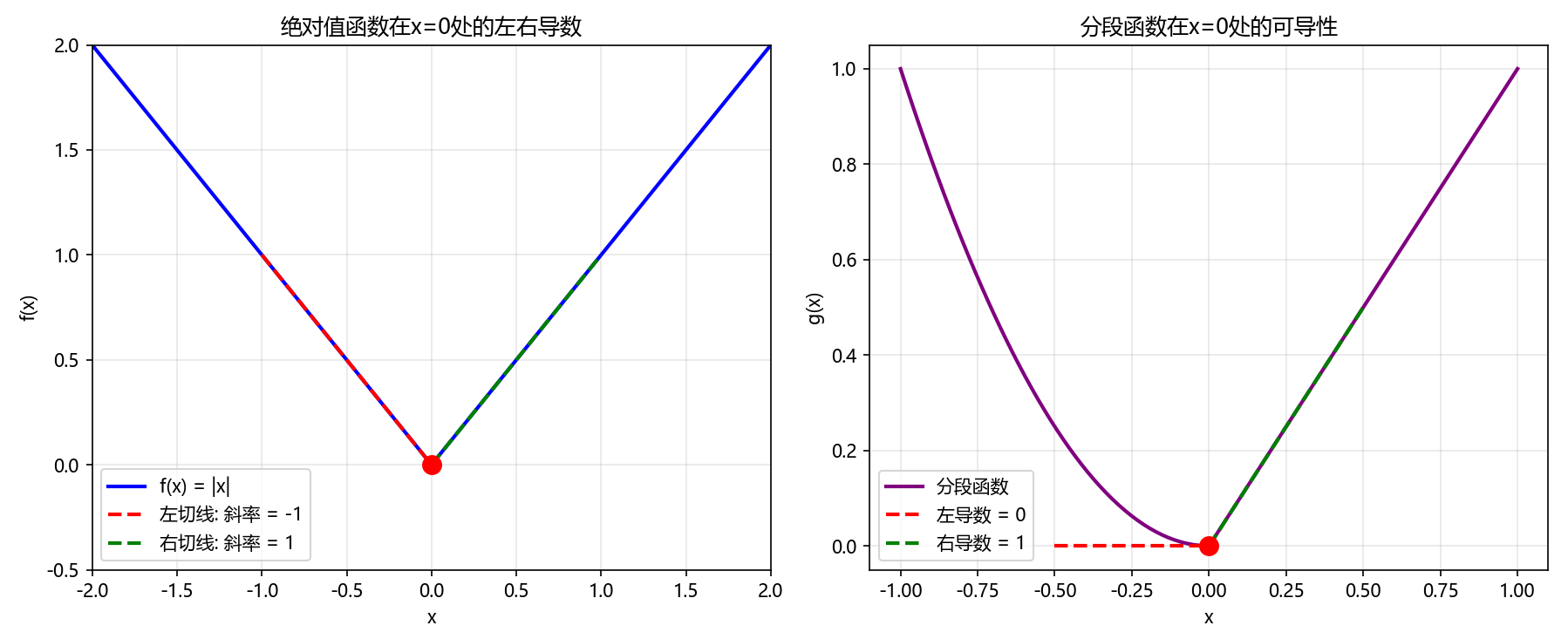
Python可视化:绝对值函数的单侧导数
def demonstrate_one_sided_derivatives():"""演示单侧导数的几何意义"""x_left = np.linspace(-2, 0, 100)x_right = np.linspace(0, 2, 100)f = lambda x: np.abs(x)# 计算左右导数left_derivative = -1 # 左导数right_derivative = 1 # 右导数plt.figure(figsize=(12, 5))# 函数图像plt.subplot(1, 2, 1)plt.plot(x_left, f(x_left), 'b-', linewidth=2, label='f(x) = |x|')plt.plot(x_right, f(x_right), 'b-', linewidth=2)# 左右切线x_tangent_left = np.linspace(-1, 0, 50)left_tangent = left_derivative * x_tangent_leftplt.plot(x_tangent_left, left_tangent, 'r--', linewidth=2, label=f'左切线: 斜率 = {left_derivative}')x_tangent_right = np.linspace(0, 1, 50)right_tangent = right_derivative * x_tangent_rightplt.plot(x_tangent_right, right_tangent, 'g--', linewidth=2, label=f'右切线: 斜率 = {right_derivative}')plt.scatter([0], [0], color='red', s=100, zorder=5)plt.title('绝对值函数在x=0处的左右导数')plt.xlabel('x')plt.ylabel('f(x)')plt.legend()plt.grid(True, alpha=0.3)plt.axis([-2, 2, -0.5, 2])# 另一个例子:分段函数plt.subplot(1, 2, 2)x1 = np.linspace(-1, 1, 100)g = lambda x: np.piecewise(x, [x < 0, x >= 0], [lambda x: x**2, lambda x: x])plt.plot(x1, g(x1), 'purple', linewidth=2, label='分段函数')# 在x=0处的左右导数g_left_deriv = 0 # (x²)' = 2x, 在x=0处为0g_right_deriv = 1 # (x)' = 1x_left_tangent = np.linspace(-0.5, 0, 50)left_tangent_g = g_left_deriv * x_left_tangentplt.plot(x_left_tangent, left_tangent_g, 'r--', linewidth=2, label=f'左导数 = {g_left_deriv}')x_right_tangent = np.linspace(0, 0.5, 50)right_tangent_g = g_right_deriv * x_right_tangentplt.plot(x_right_tangent, right_tangent_g, 'g--', linewidth=2, label=f'右导数 = {g_right_deriv}')plt.scatter([0], [0], color='red', s=100, zorder=5)plt.title('分段函数在x=0处的可导性')plt.xlabel('x')plt.ylabel('g(x)')plt.legend()plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()demonstrate_one_sided_derivatives()
运行结果:
三、导数的几何意义:切线与变化率的可视化理解
3.1 切线斜率的精确化
从几何角度看,导数 f′(x0)f'(x_0)f′(x0) 表示曲线 y=f(x)y=f(x)y=f(x) 在点 P0(x0,f(x0))P_0(x_0, f(x_0))P0(x0,f(x0)) 处的切线斜率。
割线到切线的演变过程:
- 割线斜率:通过点 P0(x0,f(x0))P_0(x_0, f(x_0))P0(x0,f(x0)) 和 P(x,f(x))P(x, f(x))P(x,f(x)) 的割线斜率为 f(x)−f(x0)x−x0\frac{f(x)-f(x_0)}{x-x_0}x−x0f(x)−f(x0)
- 切线定义:当 x→x0x \to x_0x→x0 时,割线 P0PP_0PP0P 趋近于一个极限位置,这个极限位置的直线称为曲线在点 P0P_0P0 处的切线
- 切线斜率:切线斜率即为割线斜率的极限值:k=limx→x0f(x)−f(x0)x−x0=f′(x0)k = \lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0} = f'(x_0)k=limx→x0x−x0f(x)−f(x0)=f′(x0)
3.2 切线方程与法线方程
知道切线斜率后,我们可以写出:
- 切线方程:y−f(x0)=f′(x0)(x−x0)y - f(x_0) = f'(x_0)(x - x_0)y−f(x0)=f′(x0)(x−x0)
- 法线方程(与切线垂直的直线):y−f(x0)=−1f′(x0)(x−x0)y - f(x_0) = -\frac{1}{f'(x_0)}(x - x_0)y−f(x0)=−f′(x0)1(x−x0)(当 f′(x0)≠0f'(x_0) \neq 0f′(x0)=0)
Python可视化:导数与切线关系
def demonstrate_tangent_line():"""演示导数的几何意义:切线斜率"""# 定义函数和点f = lambda x: np.sin(x) + 0.1*x**2x0 = 1.5derivative_at_x0 = np.cos(x0) + 0.2*x0 # f'(x) = cos(x) + 0.2xx = np.linspace(0, 3, 1000)y = f(x)plt.figure(figsize=(12, 5))# 主图:函数曲线和切线plt.subplot(1, 2, 1)plt.plot(x, y, 'b-', linewidth=2, label='f(x) = sin(x) + 0.1x²')plt.scatter([x0], [f(x0)], color='red', s=100, zorder=5)# 切线tangent_line = f(x0) + derivative_at_x0 * (x - x0)plt.plot(x, tangent_line, 'r--', linewidth=2, label=f'切线: 斜率 = {derivative_at_x0:.3f}')# 割线(不同Δx值)for dx in [1.0, 0.5, 0.2]:x1 = x0 + dxslope_secent = (f(x1) - f(x0)) / (x1 - x0)secent_line = f(x0) + slope_secent * (x - x0)plt.plot(x, secent_line, ':', alpha=0.7, label=f'割线(Δx={dx}): 斜率 = {slope_secent:.3f}')plt.title('从割线到切线的演变过程')plt.xlabel('x')plt.ylabel('f(x)')plt.legend()plt.grid(True, alpha=0.3)# 局部放大图plt.subplot(1, 2, 2)x_zoom = np.linspace(x0-0.5, x0+0.5, 200)y_zoom = f(x_zoom)tangent_zoom = f(x0) + derivative_at_x0 * (x_zoom - x0)plt.plot(x_zoom, y_zoom, 'b-', linewidth=2, label='f(x)')plt.plot(x_zoom, tangent_zoom, 'r--', linewidth=2, label='切线')# 标记点和斜率plt.scatter([x0], [f(x0)], color='red', s=100, zorder=5)plt.annotate(f'点P({x0:.1f}, {f(x0):.2f})', (x0, f(x0)), xytext=(x0+0.1, f(x0)-0.2))plt.title('切线斜率的局部放大图')plt.xlabel('x')plt.ylabel('f(x)')plt.legend()plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()demonstrate_tangent_line()
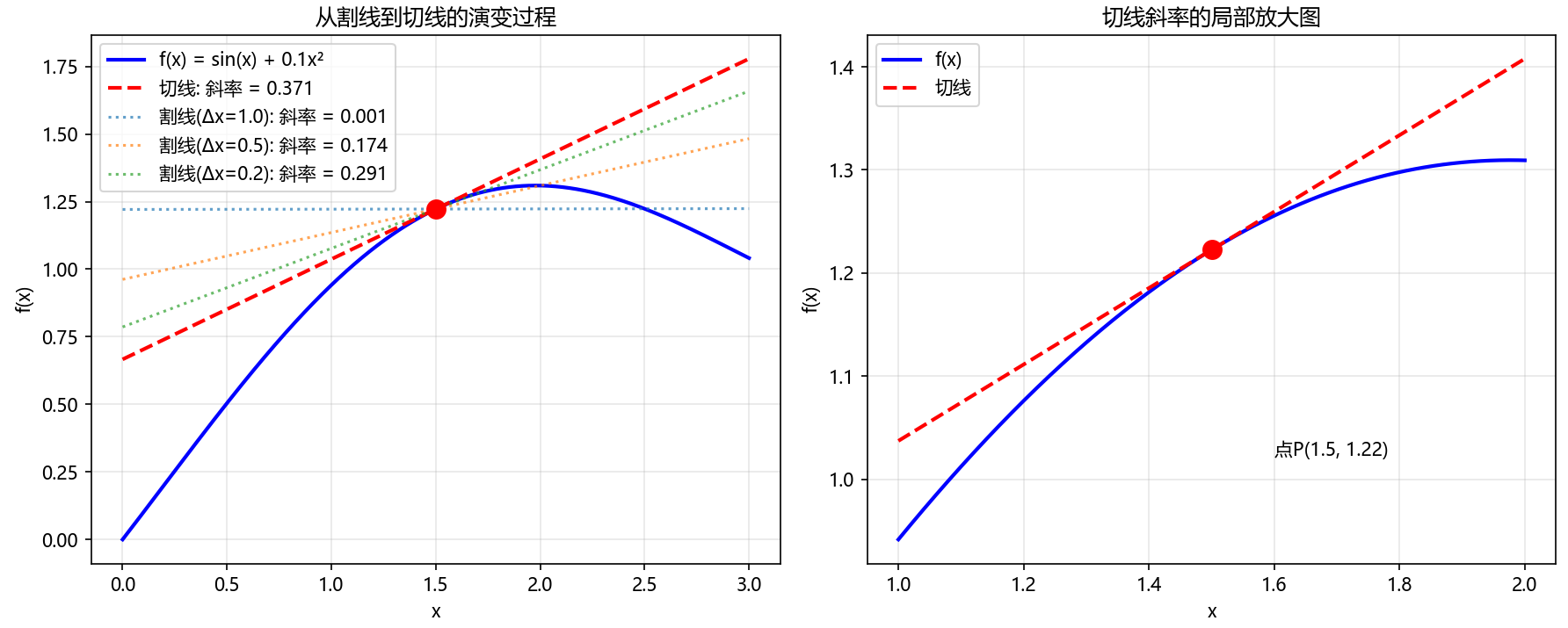
四、函数在一点可导与连续的关系
4.1 重要定理:可导必连续
这是一个微积分中的基本定理:如果函数 f(x)f(x)f(x) 在点 x0x_0x0 处可导,那么它在点 x0x_0x0 处一定连续。
证明思路: 如果 f(x)f(x)f(x) 在 x0x_0x0 处可导,则极限 limΔx→0f(x0+Δx)−f(x0)Δx\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}limΔx→0Δxf(x0+Δx)−f(x0) 存在(设为 f′(x0)f'(x_0)f′(x0))。考虑: limΔx→0[f(x0+Δx)−f(x0)]=limΔx→0f(x0+Δx)−f(x0)Δx⋅Δx=f′(x0)⋅0=0\lim_{\Delta x \to 0} [f(x_0+\Delta x)-f(x_0)] = \lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \cdot \Delta x = f'(x_0) \cdot 0 = 0Δx→0lim[f(x0+Δx)−f(x0)]=Δx→0limΔxf(x0+Δx)−f(x0)⋅Δx=f′(x0)⋅0=0 这说明 limΔx→0f(x0+Δx)=f(x0)\lim_{\Delta x \to 0} f(x_0+\Delta x) = f(x_0)limΔx→0f(x0+Δx)=f(x0),即 f(x)f(x)f(x) 在 x0x_0x0 处连续。
4.2 逆命题不成立:连续不一定可导
关键点:连续只是可导的必要条件而非充分条件。存在许多函数在一点连续但不可导的例子:
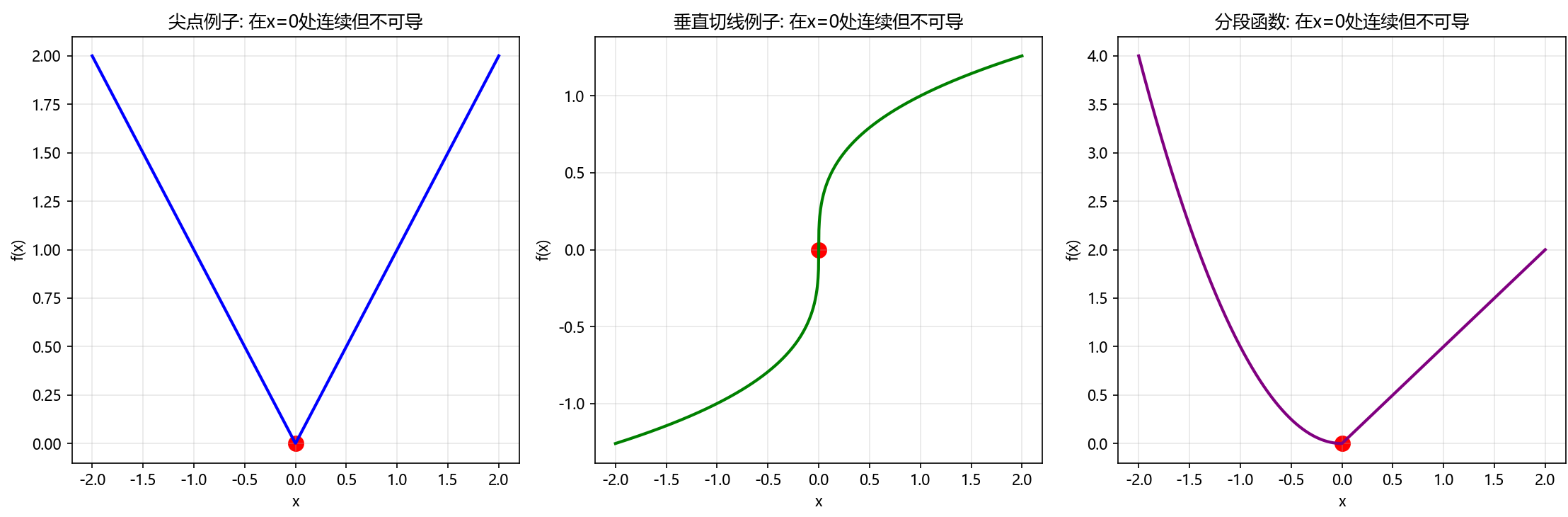
- 尖点例子:f(x)=∣x∣f(x)=|x|f(x)=∣x∣ 在 x=0x=0x=0 处连续但不可导(左右导数不相等)
- 垂直切线例子:f(x)=x3f(x)=\sqrt[3]{x}f(x)=3x 在 x=0x=0x=0 处连续但导数无穷大
- 振荡例子:某些病态函数可能处处连续但处处不可导
Python可视化:连续但不可导的函数
def demonstrate_continuous_but_not_differentiable():"""演示连续但不可导的函数例子"""x = np.linspace(-2, 2, 1000)plt.figure(figsize=(15, 5))# 例子1:绝对值函数(尖点)plt.subplot(1, 3, 1)y1 = np.abs(x)plt.plot(x, y1, 'b-', linewidth=2, label='f(x) = |x|')plt.scatter([0], [0], color='red', s=100)plt.title('尖点例子: 在x=0处连续但不可导')plt.xlabel('x')plt.ylabel('f(x)')plt.grid(True, alpha=0.3)# 例子2:立方根函数(垂直切线)plt.subplot(1, 3, 2)y2 = np.cbrt(x)plt.plot(x, y2, 'green', linewidth=2, label='f(x) = ∛x')plt.scatter([0], [0], color='red', s=100)plt.title('垂直切线例子: 在x=0处连续但不可导')plt.xlabel('x')plt.ylabel('f(x)')plt.grid(True, alpha=0.3)# 例子3:分段函数(跳跃导数)plt.subplot(1, 3, 3)y3 = np.piecewise(x, [x < 0, x >= 0], [lambda x: x**2, lambda x: x])plt.plot(x, y3, 'purple', linewidth=2, label='分段函数')plt.scatter([0], [0], color='red', s=100)plt.title('分段函数: 在x=0处连续但不可导')plt.xlabel('x')plt.ylabel('f(x)')plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()demonstrate_continuous_but_not_differentiable()
五、知识总结与思维导图
核心概念关系
导数概念体系
├── 一点处的导数
│ ├── 定义:Δy/Δx当Δx→0的极限
│ ├── 物理意义:瞬时变化率
│ └── 单侧导数(左导数、右导数)
│ └── 可导充要条件:左导数=右导数
├── 几何意义
│ ├── 切线斜率
│ ├── 切线方程:y-f(x₀)=f'(x₀)(x-x₀)
│ └── 法线方程
└── 可导与连续的关系├── 可导 ⇒ 连续(定理)└── 连续 ⇏ 可导(有反例)
🔍 思考题(评论区讨论)
- 几何直观:如果一个函数在某点的切线是垂直的,该点是否可导?为什么?
- 物理类比:瞬时速度为零的物体,其加速度是否一定为零?用导数概念解释。
- 反例构造:你能构造一个在x=0处连续但不可导的函数吗?(除了绝对值函数)
- 实际应用:在经济学中,边际成本是导数的概念吗?它反映了什么变化率?
💻 Python探索挑战
# 挑战1:绘制函数 f(x) = x*sin(1/x) 在x=0附近的行为,分析其在x=0处的连续性和可导性
# 挑战2:创建一个交互式可视化,让用户输入Δx值,观察平均变化率如何趋近瞬时变化率
# 挑战3:验证三次函数 f(x) = x³ 在所有点都可导,并解释为什么
下节预告:在下一篇文章中,我们将学习微分的概念及其应用,包括微分的定义、几何意义、与导数的关系,以及微分在近似计算和误差估计中的实际应用。
参考资料:
- 同济大学《高等数学》第七版
- 扈志明《微积分》教材
互动邀请:如果你对导数概念有独特的理解或在实际应用中遇到过有趣的问题,欢迎在评论区分享交流!
