华为OD算法开发指导-比赛的冠亚季军

算法描述

存在N个运动员，他们的id编号为0到N-1，他们的实力值用N个正整数表示，其中，N的范围在[3,10000]，比赛的规则为，每轮相邻的运动员之间举行比赛，例如，id编号为0的运动员与id编号为1的运动员之间举行比赛，id编号为2的运动员与id编号为3的运动员之间举行比赛，以此类推，当N为奇数时，id编号为N-1的运动员直接晋级到下一轮比赛，运动员的实力值大者为胜，当运动员的实力值相等，则id编号小者为胜，直到最后一轮决赛，决出前三名的冠亚季军。

输入描述

输入一行N个正整数，表示N个远动员的实力值。

输出描述

输出前三名冠亚季军的id编号以及实力值。

测试用例

输入： 99 98 92 97 96 96 95

输出： TOP1,id:0,value:99 TOP2,id:4,value:96 TOP3,id:3,value:97

算法逻辑分析

使用二维数组记录参赛的运动员，二维数组的每个元素表示一个运动员，其数据结构：[[0,93],[1,96],[2,98]]，其中，[0,93]表示id编号为0的运动员的实力值是93，以此类推。

使用递归算法，每次递归表示举办一轮比赛，在每轮比赛中，循环地对相邻的运动员举行比赛，将胜者保存在二维数组中，保存的位置从二维数组的索引0开始计算，将该轮比赛的结果对应的二维数组以及运动员的总数传入到下一次的递归算法中，以此类推，最后一次递归比赛结束，返回包括冠亚季军的二维数组。

比赛条件判断，循环地对相邻的运动员举行比赛的时候，如果N为偶数，则循环的开始条件为0结束条件为N-1，如果N为奇数，循环的开始条件为0结束条件为N-2，N-1索引位置的运动员直接进入下一轮比赛。 胜负条件判断，运动员的实力值大者为胜，当运动员的实力值相等，则id编号小者为胜。 冠军条件判断，当N为3或者4，循环地对相邻运动员举行比赛，最后决出冠亚军。 季军条件判断，当N为3或者4，在二维数组的前3位或者4位运动员中，除去冠亚军，剩下的1位运动员或者2位运动员中的胜者为季军。

Java算法代码

主函数以及测试函数：

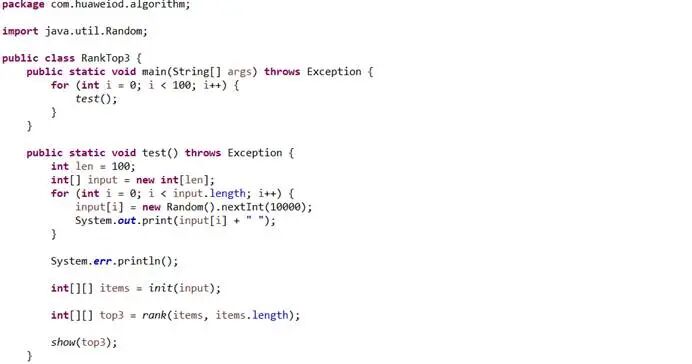
显示冠亚季军的信息：

初始化输入的运动员数据到指定的数据结构中：

比赛递归主函数：

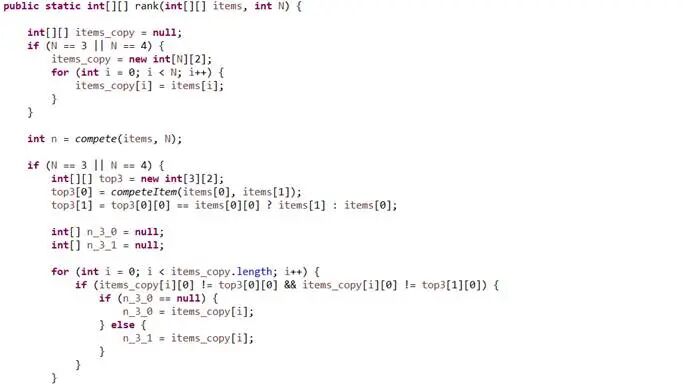
比赛轮次主函数：

运动员比赛函数：

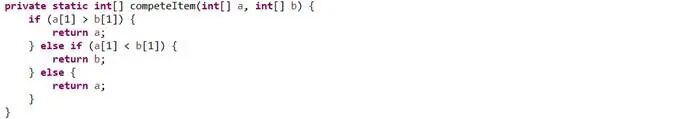
算法测试

12位运动员的测试数据：

13位运动员的测试数据：

20位运动员的测试数据：