当前位置：首页 > news >正文

神经学习（4）神经网络的向量化实现与TensorFlow训练流程

news 2025/10/27 12:59:14

一、向量化实现神经网络中的前向传播

1. 前向传播的基本过程

神经网络的核心思想是“输入 → 线性变换 → 激活函数 → 输出”。例如在一个简单的两层神经网络中：

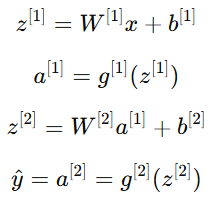
其中：

x：输入向量（input vector）
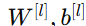：第 lll 层的参数（权重与偏置）
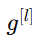：激活函数（activation function）
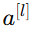：第 lll 层的输出（也称为激活值）

2. 非向量化与向量化的区别

（1）非向量化实现

早期写法中，我们可能会用循环遍历每个样本或每个神经元：

for i in range(m):z[i] = np.dot(W, x[i]) + ba[i] = sigmoid(z[i])

这种方式逻辑清晰，但在处理大量样本时效率极低，因为循环会反复进行矩阵运算。

（2）向量化实现

向量化（Vectorization）可以通过 NumPy 的矩阵运算一次性完成所有样本的计算：

Z = np.dot(W, X) + b
A = sigmoid(Z)

这样不仅更简洁，而且可以充分利用底层的 BLAS / GPU 并行计算，使得速度提升几十倍到上百倍。

优点总结：

避免显式循环，提高运算效率；
代码更简洁易读；
便于与深度学习框架（TensorFlow、PyTorch）集成。

二、如何在 TensorFlow 中训练神经网络

TensorFlow（TF）高度封装了神经网络的训练过程，可以通过三个主要步骤实现：

1. 指定模型结构（Define the Model）

你需要定义网络层的结构，比如输入层、隐藏层、输出层。

import tensorflow as tf
from tensorflow import kerasmodel = keras.Sequential([keras.layers.Dense(10, activation='relu', input_shape=(2,)),keras.layers.Dense(1, activation='sigmoid')
])

2. 编译模型（Compile the Model）

编译模型时，需要指定：

损失函数（Loss Function）：用于衡量预测与真实值的差距；
优化器（Optimizer）：用于更新参数；
评估指标（Metrics）：用于监控训练效果。

model.compile(optimizer='adam',loss='binary_crossentropy',metrics=['accuracy'])

3. 训练模型（Train the Model）

使用 .fit() 方法进行训练：

model.fit(X_train, y_train, epochs=50, batch_size=32)

三、训练细节：逻辑回归与神经网络

训练逻辑回归（Logistic Regression）或神经网络的步骤非常类似：

1. 指定如何计算输出

给定输入 x 和参数 W,b，模型计算预测输出：

2. 指定损失函数

对于二分类问题，常用 二元交叉熵损失函数（Binary Cross Entropy Loss）：

这里的 “二元” 指的是输出只有两类：0 或 1。

3. 调用优化算法

优化器会自动计算梯度并最小化损失函数，例如使用梯度下降（Gradient Descent）或 Adam 优化器。

四、常见激活函数（Activation Functions）

激活函数决定了神经网络的非线性特征，不同任务中会选择不同的函数：

激活函数	特点	常用场景
线性函数（Linear）	无非线性	回归任务
Sigmoid	输出范围 (0,1)，可解释为概率	二分类输出层
ReLU（Rectified Linear Unit）	收敛快，避免梯度消失	隐藏层常用
Softmax	多分类概率分布	多分类输出层