高级机器学习作业（一）岭回归 + 信息熵 + Sigmoid + Softmax + PCA
目录
1. 最小二乘与岭回归
1.1 中心化
2. 信息熵与信息增益
1. 信息熵的上下界
2. 证明信息增益非负
3. Sigmoid 与 Softmax
3.1 Sigmoid
3.2 多元与Softmax l对β求导
3.3 Sigmoid 与 Softmax 关系
4. PCA 降维
4.1 X^T X
4.2 奇异值分解
4.3 将下列矩阵降至二维
1. 最小二乘与岭回归
左右把逆都乘到对面，X (X^T X + λI) = (X*X^T + λI) X
（2）给出岭回归 w*，b*的闭式解表达式，并与原始线性回归的结果比较。
闭式解 指的是可以通过显式的数学表达式直接求解的解，不需要通过迭代、逼近等数值方法。
岭回归则设置正则项 Ω(w) = ||w||^2
对 w 求偏导：
对 b 求偏导：
把 b代入，并整理得：
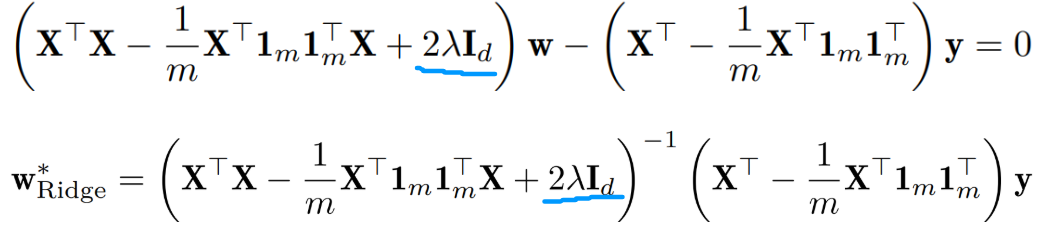
与普通最小二乘相比，b*是一样的，w*前面的 逆多了一项 2λI，
新增的一项能够避免矩阵的特征值趋于 0，从而方便矩阵的求逆操作。
1.1 中心化
z 先乘上一个全1行向量，得到每列求和，除以m即为每列平均值。
再乘上纵向量 1，即每列都减去均值。
目的：通过中心化，让 “均值信息” 被偏置b 单独捕捉，w捕捉特征波动对标签的影响。
可把之前的 w* 简化为：
2. 信息熵与信息增益
1. 信息熵的上下界
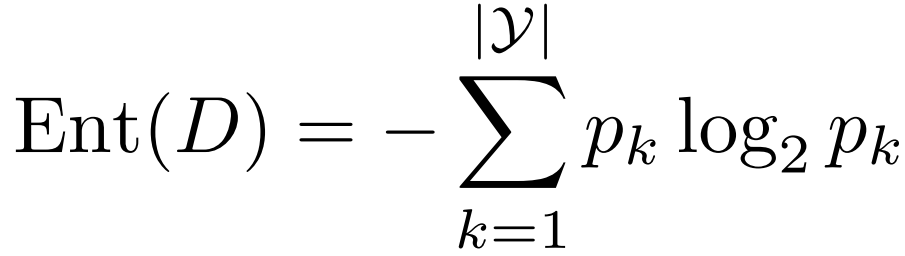证明 
信息熵下界：全是同一类，结果即为0
上界：p*log(1/p) Jensen不等式 （系数移到里面 正好是1） log x 是凹函数
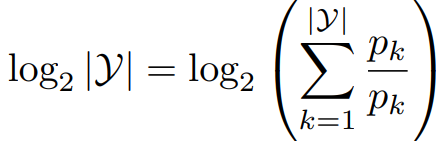
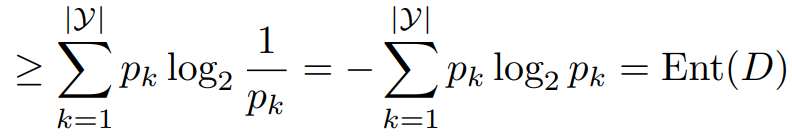
2. 证明信息增益非负
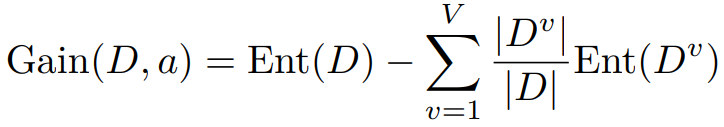
定义随机变量 Y 为类别标记，定义随机变量 A 为属性 a 的取值。可得条件熵 H(Y|A)为
即为对 A,Y的二维求和：
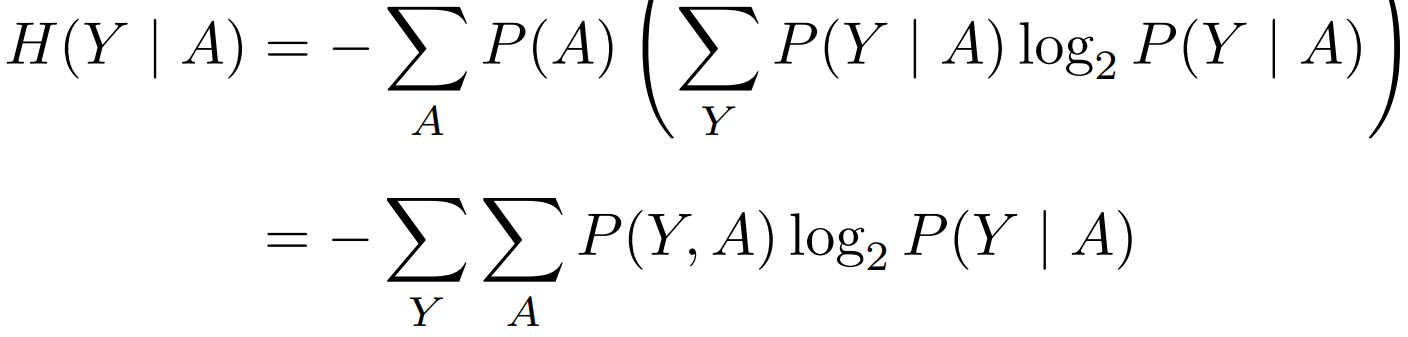
信息增益即可写为 H(Y) - H(Y|A).
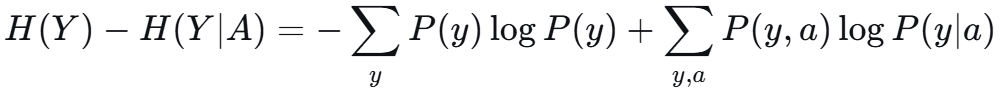
前者也拆为 二维累加
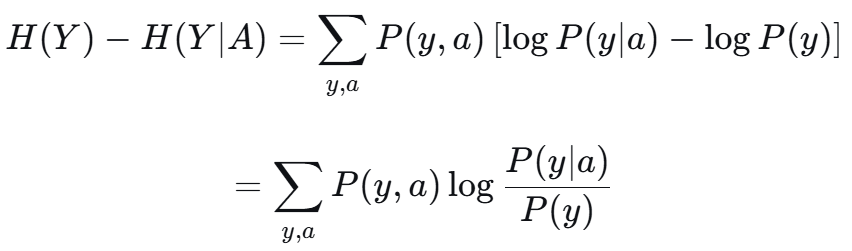
可以看做 P = P(y,a) Q = P(y)P(a) 两个分布的 KL散度 是非负的。
3. Sigmoid 与 Softmax
3.1 Sigmoid
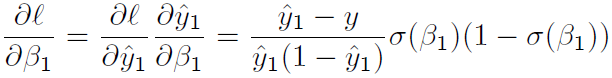
3.2 多元与Softmax l对β求导
多元损失函数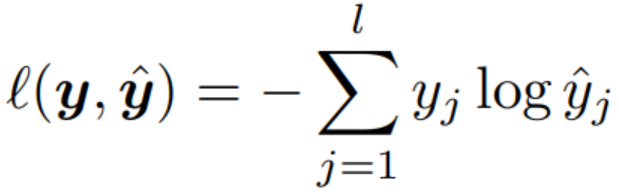
Softmax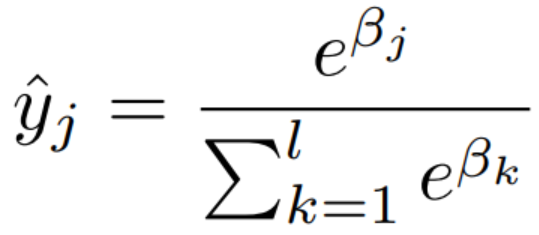 
单元素求导与整个向量：
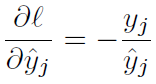
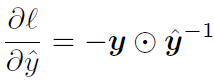逐元素除法
对 Softmax 求导，分母设为 Z。yi 对 βj 求导，
若 i ≠ j，分子是常数，即为 
若 i = j，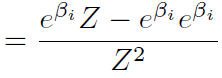
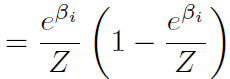
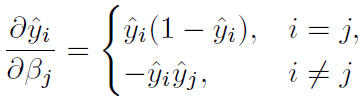写成矩阵形式为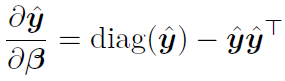 
链式法则相乘得：
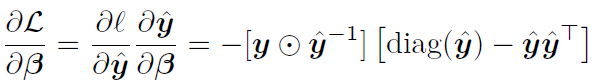
3.3 Sigmoid 与 Softmax 关系
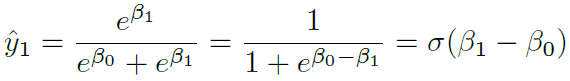
所以 Softmax 函数可以看成 Sigmoid 函数在多分类问题中的一个推广。
4. PCA 降维
给定 d 维空间中 m 个样本构成的矩阵为 
下面的讨论中 忽略系数 1/(m-1)
4.1 X^T X
二者的特征值有什么联系？受此启发，请思考当特征维度远大于样本个数时(d ≫ m)，使用特征值分解求解PCA 应如何执行将更加高效？
对称，并且
d>>m时，X^T X 是d*d的，X X^T是m*m的，后者小 所以特征值分解的成本 d*m^2 低于前者。
启发：d>>m 时，先算 X X^T 的特征值 λ 和特征向量 u，通过 X^T u 得到 X^T X 的特征向量。
4.2 奇异值分解
对角线元素从大到小排序，截胡非零项前 r 个。
维度分别为 (m*r) * (r*r) * (r*d)
在实现 PCA 时，往往使用奇异值分解(SVD) 而非特征值分解求解。
（1）请说明奇异值与特征值的关系。
所以 协方差矩阵的特征值分解的向量矩阵 -> 对应奇异值分解的向量矩阵。
特征值为奇异值的平方。
（2）如果可以获得 X 的奇异值分解，应如何使用PCA 对 X 进行降维？
对 d 维度进行截尾，
V的列向量即为投影特征向量， U Σ 即为降维后的结果。
（3） 请分析使用SVD 求解PCA 相比于使用特征值分解求解PCA 的优势。
时间复杂度分析：
都要（1）数据中心化：遍历整个矩阵来计算每个特征的均值并减去它。 O(m*d)
（2）计算协方差矩阵 O(d*m*d) d*d 的矩阵特征值分解 O(d^3)
如果是 SVD 复杂度 O(min(m,d)*m*d)，随机 SVD 复杂度 O (k*m*d)
4.3 将下列矩阵降至二维
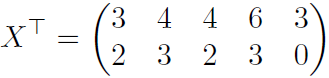
对 X 求列均值为 (4,2) 中心化后为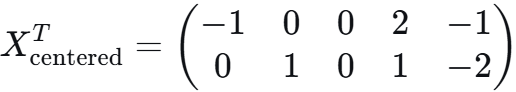 
协方差矩阵求特征值和特征向量
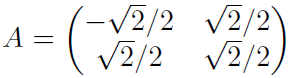
投影与变换回来 分别为
