机器学习日报05

摘要

今天的学习主要围绕神经网络的不同类型和模型评估方法展开。首先，我了解了除了常见的密集层之外，还有像卷积层这样更高效的网络结构。卷积层通过让每个神经元只关注输入数据的局部区域，不仅加快了计算速度，还减少了过拟合的风险。接着，我学习了如何系统评估模型性能，重点掌握了将数据集划分为训练集、交叉验证集和测试集的方法，以及它们各自在模型训练和选择中的作用。这些内容帮助我理解了如何更科学地构建和优化机器学习模型。

Abstract

Today’s study focused on different types of neural networks and methods for model evaluation. I first explored convolutional layers, which differ from dense layers by having each neuron process only a limited region of the input. This design improves computational efficiency and reduces overfitting. I then learned systematic approaches to evaluate model performance, including splitting data into training, cross-validation, and test sets. These subsets play distinct roles in training models, selecting parameters, and providing unbiased estimates of generalization error. This knowledge is crucial for building robust and effective machine learning systems.

一、不同类型的神经网络

到目前为止，我们使用的所有神经网络都是密集层，其中每个层中的每个神经元都将前一层的所有激活作为输入，事实证明，还有一些具有其他特征的层类型

回顾一下，我们一直在使用的密集层

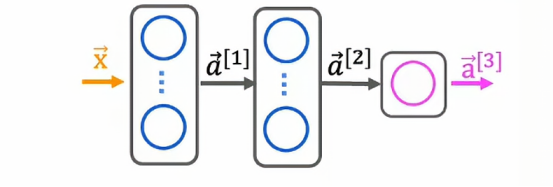
神经元的激活是依赖上一层的输出，比如上图的第二隐藏层的输出a2，其实是依靠第一隐藏层的输出a1

1、卷积层

有时设计神经网络的人可能会选择使用不同类型的层，在一些工作中我们可能会看到另一种层类型叫做卷积层，让我们用一个例子来说明这一点，这是手写的数字9

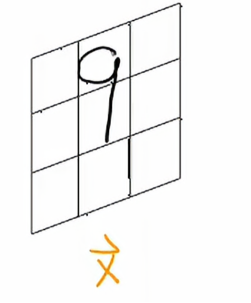
我要做的是构建一个隐藏层，它将计算不同的激活值作为此输入图像x的函数

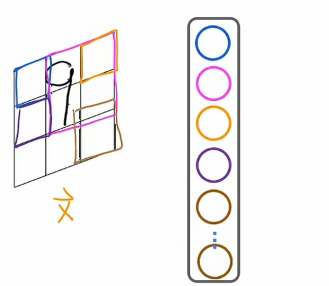
对于第一个神经元，我们用蓝色标记出来，这个蓝色神经元只能查看这个小矩形区域中的像素，第二个神经元，我们用洋红色标记出，他只能查看图像中有限区域的像素，第三个神经元也是如此，第四个神经元也是如此，直到最后一个神经元，它只能查看图像中的某个区域。

为什么使用这样的神经网络，首先它加快了计算速度，第二个优势是使用这种类型层的神经网络更不容易过拟合

这种类型的神经网络，每个神经网络只查看输入图像的一个区域，称为卷积层

1、例子：心电图

我们再来看一个例子，这次为了更好地理解卷积层，我们引入一个一维的例子，就是我们经常在医院看到的心电图

现在我们是医疗团队中的一员，我们负责记录电压，看起来像这样的心跳对应信号

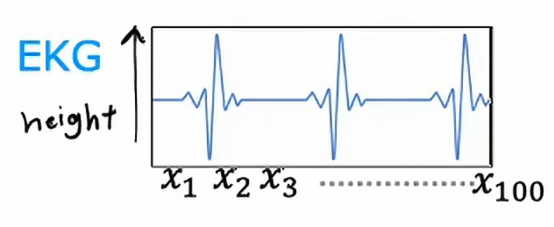
我们正在读取类似这样的心电信号，以尝试诊断患者是否有心脏问题，EKG则是表示对于不同时间点该表面高度的数字列表，100个信号对应这条曲线在100个不同时间点的高度，学习任务是来分类是否患者患有心脏病或者某种可诊断的心脏状况

现在，让我们把心电图旋转90

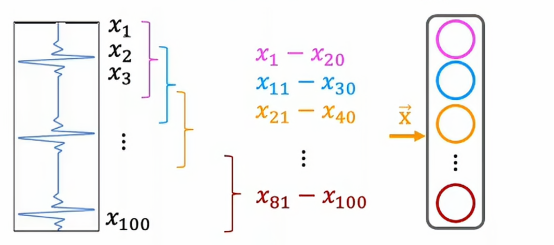
从上往下看第一个神经元负责的是x1到x20这段心电图，而第二个负责x11到x30、第三个负责的是x21到x40，最后一个负责的是x81到x100，按照上面我们介绍的卷积层概念，我们能够很容易判断出来这是一个卷积层，因为每个神经元都之查看输入的有限窗口，而在下一层，我们同样能创造一个卷积层

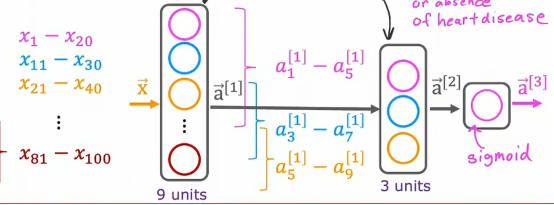
下一层的神经元从上往下我们可以看到，第一个负责查看上一层的a1到a5，第二个负责查看a3到a7，第三个负责查看a5到a9，然后最后输出层选择一个sigmoid函数，因为我们最终的目标是对心脏病的二元判断，用sigmoid函数再合适不过了

由此我们可以看出卷积层在某些方面的效率是比密集层的效率要高的

二、模型评估

假设我们已经训练了一个机器学习模型，我们应该如何评估模型的性能？我们会发现拥有一个系统的方法来评估性能，也将有助于为接下来的步骤指明更清晰的道路，那么，我们来看看如何评估一个模型

1、平方误差成本的回归

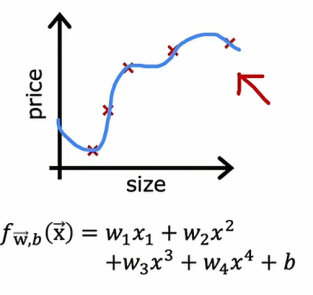
让我们以根据房屋面积预测房价为例，假设我们已经训练了一个模型，用来根据面积x预测房价，对于模型，它是一个四阶多项式

从图中我们可以看出，我们用了五个数据点来拟合了一个四阶多项式，但是这里有一个我们之前提到的问题，就是尽管该模型适合训练数据，但无法推广到不在训练集中的新示例，所以仅用房屋面积这个单一特征来预测价格时，我们可以看到曲线非常波动，因此我们知道这可能不是一个好模型，但是如果我们用更多的特征来拟合这个模型，比如我们有x1房屋面积、卧室数量、房屋的楼层数、房子的年龄，然后绘制f就变得困难了，因为f现在是x1到x4的函数，我们该如何绘制一个思维函数？

所以为了判断我们的模型表现是否良好，特别是在有多于一或两个特征的应用中，我们需要一个更系统的方法来评估我们的模型表现如何

这里有一个办法，这里有一个10个示例的小型训练集，但是我们不用所有数据来训练模型，而是给它们分为两个子集

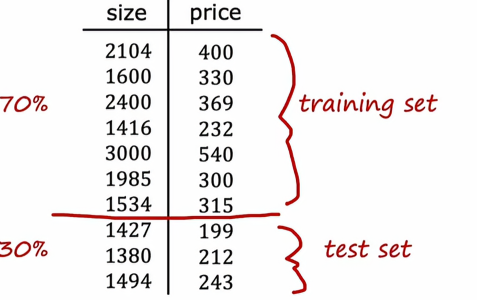
我们将上方的百分之70放入训练集当中，将下面的百分之20放入测试集中，训练集就是训练模型的参数，而测试集，顾名思义就是测试模型的性能，这里需要说明一下，在符号表示上需要区别两者：

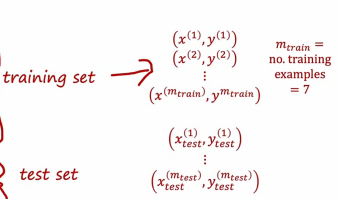
大部分数据都是划入到训练集上，只有小部分被放入测试集上，因此，为了训练一个模型并对其进行评估，如果我们用的是带有平方误差的线性回归，结果将是这样

首先通过最小化成本函数的j的wb来拟合参数，这是一种常见的成本函数，然后我们看Jtest,m是测试样本的数量，需要注意的是测试误差公式中没有正则化参数，这将让我们了解我们的学习算法表现如何另外一个很有用的参数是训练误差，这是衡量我们的学习算法在训练集上的表现情况

结合我们在本节开始时的图片，Jtrain会很低，因为我们的样本都拿来训练模型了，所以平均误差非常接近0，但如果我们是把数据集分成2个部分的话，可能看起来是这样的

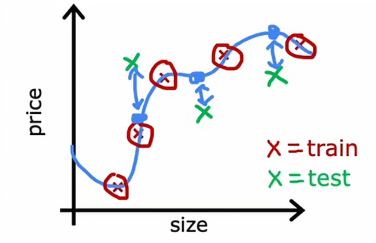
这样算法预测的房价估计值与实际值之间有很大的差距，所以Jtest会很高，这样会让我们意识到即使它在训练模型上表现好，但它实际上并不能很好地泛化到新样本上，所以这是平方误差成本的回归

2、分类问题的评估

现在让我们看看如何将这个过程应用到分类问题中去，例如我们在分别手写数字0和1
，与之前一样，我们会通过最小化代价函数来拟合参数，从而找到参数wb，例如我们现在在训练逻辑回归，那么这些参数的计算如下图所示：

实际上还有另外一种定义Jtest和jtrain更为常用，就是不使用逻辑损失来计算测试误差和训练误差，而是测量算法在测试集和训练集中分类错误的比例，具体来说在测试集上，算法可以对每个测试样本做出0或1的预测，回想一下，若f(x)大于等于0.5我们就预测y-hat为1，如果小于0.5则预测为0，然后我们可以统计测试函数集中y-hat不等于实际真实值的样本比例，在测试集中的标签y，具体来说，如果我们在新的分类任务中对手写数字0或1进行分类，那么j测试就是测试集中0被分类为1或1被分类为0的比例，同样地j训练是训练集中被错误分类的比例。

将数据集分成训练集和单独的测试集，为我们提供了一种系统化的方法，评估我们的学习算法表现如何，我们现在可以衡量它在测试集和训练集上的表现如何，这个过程是自动选择一个模型用于给定机器学习任务的一个步骤。

三、模型选择和训练交叉验证测试集

在上一个小节中，我们看到了如何使用测试集来评估模型的性能，在本节中，让我们对这个想法进一步优化，它可以让我们使用一种技术，自动选择一个合适的机器学习算法的模型

我们看到的一件事，一旦模型的参数W和B适配了训练集，训练误差可能并不是很好地指示算法的表现，或者算法对新数据的泛化能力如何在训练集中没有出现的样本

特别是对于这个例子而言，这可能远低于实际的泛化误差，我的意思是指那些不在训练集中的新样本上的平均误差，我们在上一节中看到的是Jtest算法在未训练样本上的表现，这将更好地指示模型在新数据上的表现状况，当然是训练集之外的其他数据，让我们看看这如何影响我们使用测试集来为特定机器学习选择模型应用

如果我们在拟合一个函数来预测房价或解决其他回归问题，我们可能会考虑的一种模型是拟合像这样的线性模型

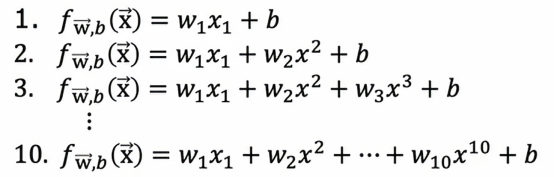
在这个例子中，我们将用d=1来表示拟合一个一阶多项式，d=2即来表示拟合一个二阶多项式，以此类推，最终到d=10，如果我们用这样的模型拟合到我们的训练集，我们会得到一些参数w和b，然后我们可以计算Jtest来估计这个模型在新数据上的泛化效果，我们可以查看从d=1到d=10，哪个Jtest值最低，假设我们发现五阶多项式的Jtest是最低的，那么我们可以认为五阶多项式d=5最优，并选择该模型应用于我们的模型，如果我们想要评估这个模型的表现，我们可以做的是报告测试集误差Jtest w5 b5。

这个程序有缺陷的原因是Jtest对于w5 b5可能是一个乐观的泛化误差估计，换句话说，它可能低于实际的泛化误差，原因是，我们在上面讨论的程序中，我们实际上拟合了一个额外的参数，即d多项式的度数，并使用测试集选择了这个参数，所以在前面，我们看到如果我们将wb拟合到训练集数据上，那么训练数据会对泛化误差产生过于乐观的估计，结果也是，如果我们使用测试集选择参数d，那么测试集Jtest现在也是过于乐观的，也就是说低于泛化误差的实际估计，因此，这一页上的程序是有缺陷的。

相反，如果我们想自动选择一个模型，比如决定使用哪个阶数的多项式，我们有一些修改和测试程序以进行模型选择的方法，通过在不同模型的选择

现在，让我们把原来的数据集分为三个部分，原来我们是分了两个部分

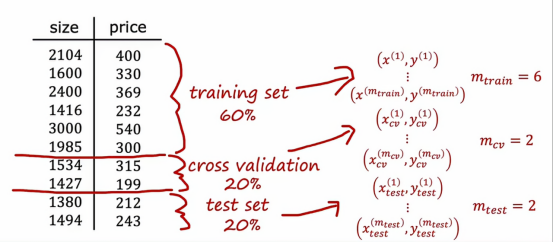
百分之60是训练集，用来训练模型，百分之20是交叉验证样本，用于使用这20的数据集来交叉检查有效性或不同模型的准确性，百分之20是测试集，用来评估模型的优劣

所以拥有这三个数据子集，训练集、交叉验证集、测试集，我们可以计算训练误差、交叉验证误差和测试误差，使用这三个公式，通常这些术语都不包括正则化项，正则化只包含在训练目标中

而中间这个新术语，交叉验证误差，只是我们交叉验证例子的平均值，例如平方误差，而这个术语，除了叫交叉验证误差，也简称为验证误差。

掌握了这三个学习算法性能的衡量标准，我们就可以进行模型选择了，让我们回到之前谈论的情况

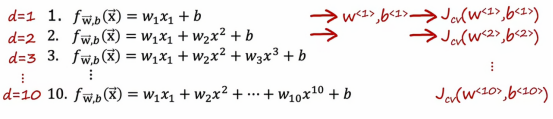
我们把误差换为交叉验证误差，我们现在验证的是看哪个模型有最低的交叉验证误差，假设当d=4时，交叉验证误差是最小的这意味着我们会选择这个四阶多项式作为你在这个应用中使用的模型，最后，如果我们想报告这个模型在新数据上的泛化误差估计，我们应该用第三个数据子集测试集并报告w4的Jtest，我们会注意到在整个过程中，我们用训练集来拟合这些参数，然后我们使用交叉验证集选择参数d或选择多项式的阶数，直到这一点，我们还没有拟合任何参数，这就是为什么在这个例子中Jtest会是对这个模型的泛化误差的公平估计，所以这提供了一种更好的模型选择程序，它可以让我们自动决定为线性回归模型选择什么阶数的多项式，这种模型选择程序同样适用于其他类型的模型选择

1、新奇角度的理解

一开始，我对这理解不来，直到我看到视频弹幕中有人举了几个例子，感觉豁然开朗了，
他说：“训练集、交叉训练集、测试集就好比考试学习，训练集就是平时老师上课讲的书本上的例题或者是课后作业上的习题；而交叉训练集是我们在校外买的模拟卷，模拟考试时的情况；而测试集就是高考，里面的题目我们都没有见过，需要通过我们平常从习题中学习的方法去解决高考中遇到的题目。”

还有一个角度的看法，有人说：“为什么加了交叉验证集，模型输出结果才是公正且不怎么乐观的？就好似我们先和一个人讨论做出决定，然后让第三个人评估，这样的结果公正合理。如果参与评估的人参与了决策，那么这个结果就不那么公平客观合理了。”

总而言之，训练集和交叉验证集用来选择模型，确定模型之后才使用测试集。

总结

今天的学习让我对神经网络的多样性和模型评估的重要性有了更深入的理解。卷积层的引入展示了如何通过结构设计提升模型的效率和泛化能力，特别是在图像、信号等数据上。而在模型评估部分，我认识到单纯依赖训练误差很容易导致过拟合，因此必须通过交叉验证和测试集来客观衡量模型在新数据上的表现。这种划分数据集的思路不仅适用于回归和分类问题，也为后续的模型选择提供了可靠依据。