当前位置：首页 > news >正文

数据结构-并查集

news 2025/10/27 10:30:32

一、并查集的核心原理

1. 初始化：每个元素都是独立集合

2. 查找（Find）：找根节点的 “路径”

3. 合并（Union）：合并两个集合

二、并查集的通用类实现

三、并查集的实战应用

案例 1：省份数量（LCR 116 / 并查集版）

案例 2：等式方程的可满足性（LeetCode 990 / 并查集版）

四、并查集的拓展应用场景

1. 图的连通分量问题

2. 网络连通性分析

3. 基因族谱与集合划分

五、总结

在算法的世界里，有一类问题总是围绕 “集合” 展开 —— 如何快速判断两个元素是否属于同一集合？如何高效合并两个集合？并查集（Union-Find Set）就是为这类问题量身定制的高效数据结构。本文将从原理、实现到多场景实战，带你彻底掌握并查集的精髓。

一、并查集的核心原理

并查集的本质是用树形结构管理多个不相交的集合，它支持三大核心操作：查找（Find）、合并（Union）、统计集合数量。其设计巧妙之处在于通过 “路径压缩” 和 “按大小合并”，将时间复杂度优化到近乎常数级别。

1. 初始化：每个元素都是独立集合

初始时，我们为每个元素创建一个独立的集合。用一个数组 _ufs 来维护元素的父节点关系：

若 _ufs[i] = -k，表示 i 是该集合的根节点，且集合大小为 k（k 为正整数）。

例如，10 个互不相关的元素（编号 0~9），初始时每个元素都是自己的根，集合大小为 1，数组表示为：_ufs = [-1, -1, -1, -1, -1, -1, -1, -1, -1, -1]

分队s1={0,6,7,8}，分队s2={1,4,9}，分队s3={2,3,5}就相互认识了，10个元素形成了三个小团体。假设右三个群主0,1,2担任队长，负责大家的出行
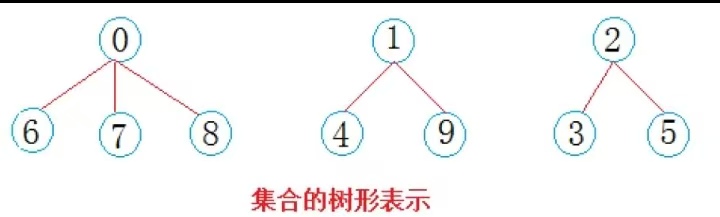
仔细观察数组中内融化，可以得出以下结论：
1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素双亲在数组中的下标

2. 查找（Find）：找根节点的 “路径”

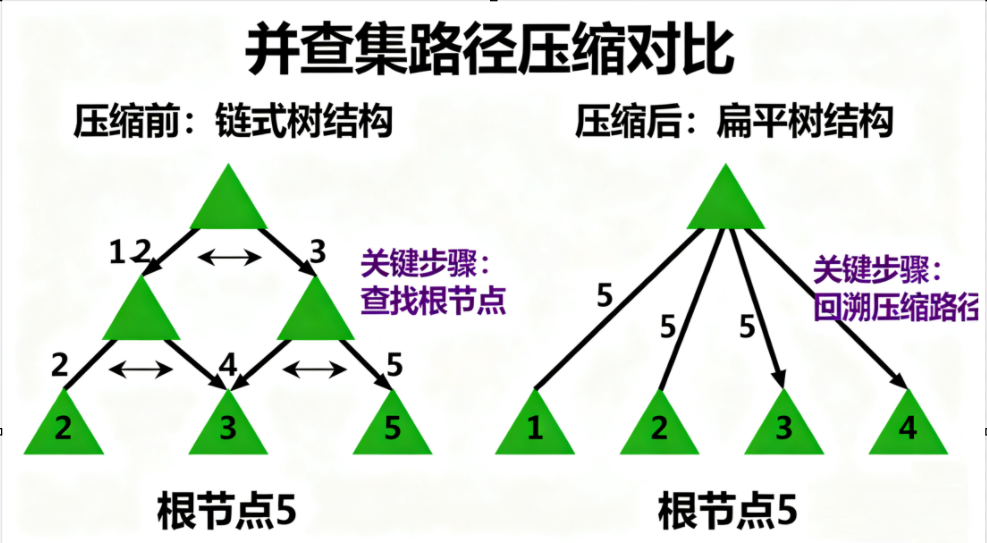
查找操作的目标是找到元素所属集合的根节点。为了避免树退化成链表，我们引入路径压缩—— 在查找过程中，将路径上的所有节点直接指向根节点，从而把树的高度压缩到最低（几乎为 1）。

路径压缩的查找函数示例：

int FindRoot(int x) {int parent = x;// 循环找到根节点（_ufs[parent] < 0 时为根）while (_ufs[parent] >= 0) {parent = _ufs[parent];}// 路径压缩（可选，递归实现更简洁）// 此处用循环实现，将路径上的节点直接指向根int root = parent;parent = x;whileuf (_s[parent] >= 0) {int next = _ufs[parent];_ufs[parent] = root;parent = next;}return root;
}

3. 合并（Union）：合并两个集合

合并操作的核心是将一个集合的根节点指向另一个集合的根节点。为了让树的高度尽可能小（避免退化），我们采用按大小合并—— 将较小的集合合并到较大的集合中。

按大小合并的函数示例：

void Union(int x1, int x2) {int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2) return; // 已同属一个集合，无需合并// 按大小合并：小集合合并到大集合中if (_ufs[root1] > _ufs[root2]) {swap(root1, root2);}_ufs[root1] += _ufs[root2]; // 大集合的大小增加_ufs[root2] = root1;       // 小集合的根指向大集合的根
}

二、并查集的通用类实现

基于上述原理，我们可以封装一个通用的并查集类 UnionFindSet，支持 “合并、查找、判断同集合、统计集合数量” 等操作：

#pragma once
#include <iostream>
#include <vector>
using namespace std;class UnionFindSet {
public:// 初始化：n个元素，每个元素自成一个集合UnionFindSet(int n) : _ufs(n, -1) {}// 合并两个元素所在的集合void Union(int x1, int x2) {int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2) return;// 按大小合并：小集合合并到大集合if (_ufs[root1] > _ufs[root2]) {swap(root1, root2);}_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}// 查找元素的根节点（带路径压缩）int FindRoot(int x) {int parent = x;// 循环找根while (_ufs[parent] >= 0) {parent = _ufs[parent];}// 路径压缩（优化后续查找效率）int root = parent;parent = x;while (_ufs[parent] >= 0) {int next = _ufs[parent];_ufs[parent] = root;parent = next;}return root;}// 判断两个元素是否在同一集合bool InSet(int x1, int x2) {return FindRoot(x1) == FindRoot(x2);}// 统计集合的数量（根节点的数量）size_t SetSize() {int size = 0;for (int i = 0; i < _ufs.size(); ++i) {if (_ufs[i] < 0) {size++;}}return size;}private:vector<int> _ufs; // 父节点数组，负数表示根，其绝对值为集合大小
};

三、并查集的实战应用

并查集的应用场景非常广泛，以下是两个典型的算法题实战案例。

案例 1：省份数量（LCR 116 / 并查集版）

题目：有n个城市，若城市a与b直接相连，b与c直接相连，则a与c间接相连。“省份” 是一组直接或间接相连的城市，求省份的数量。

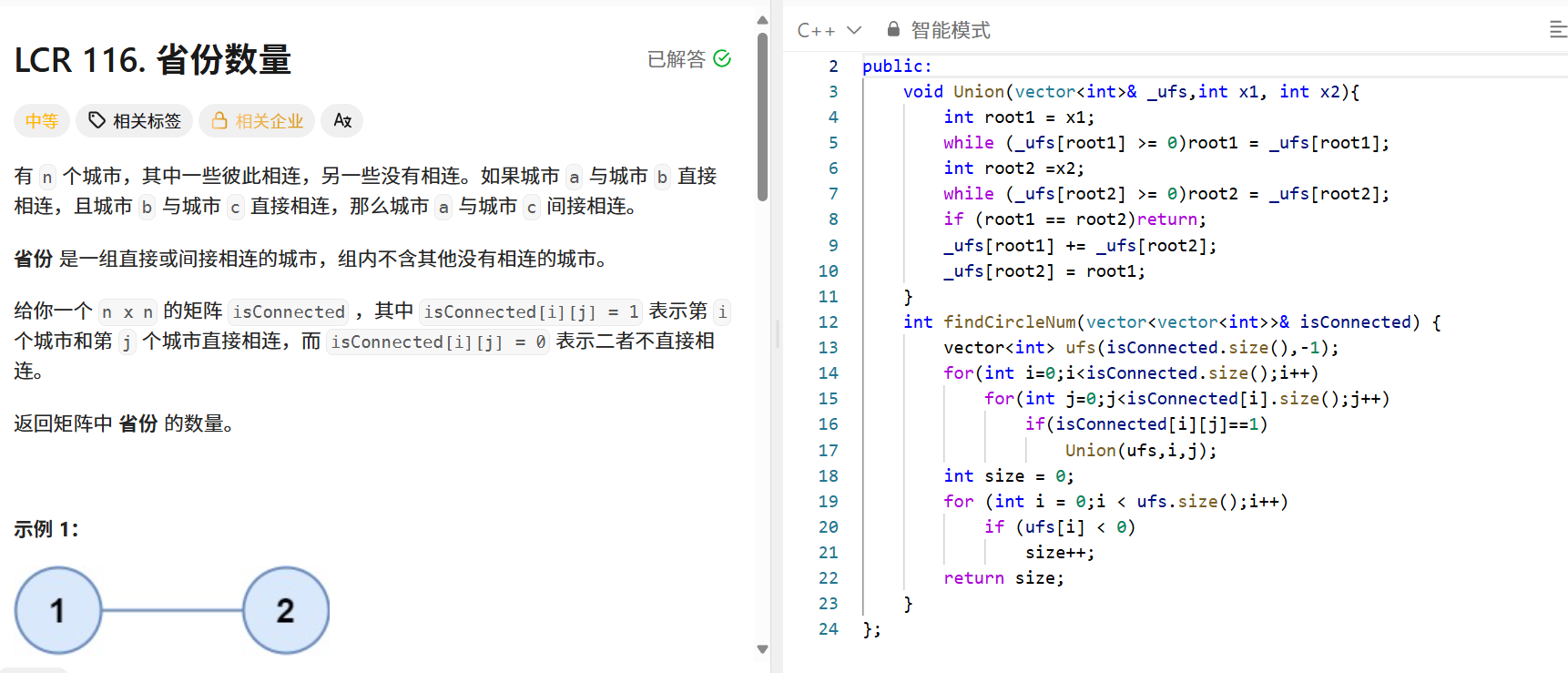
思路：

遍历城市连接矩阵，若城市i与j直接相连，则用并查集合并它们。
最终统计并查集中根节点的数量（即_ufs[i] < 0的元素个数），即为省份数量。

代码实现：

#include "UnionFindSet.hpp"
#include <vector>
using namespace std;class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {int n = isConnected.size();UnionFindSet ufs(n); // 初始化n个城市，每个城市自成一个省份// 合并直接相连的城市for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (isConnected[i][j] == 1) {ufs.Union(i, j);}}}// 统计省份数量（根节点的数量）return ufs.SetSize();}
};

案例 2：等式方程的可满足性（LeetCode 990 / 并查集版）

题目：给定一组等式（如"a==b"）和不等式（如"a!=b"），判断是否存在一种变量赋值，使得所有等式和不等式同时成立。

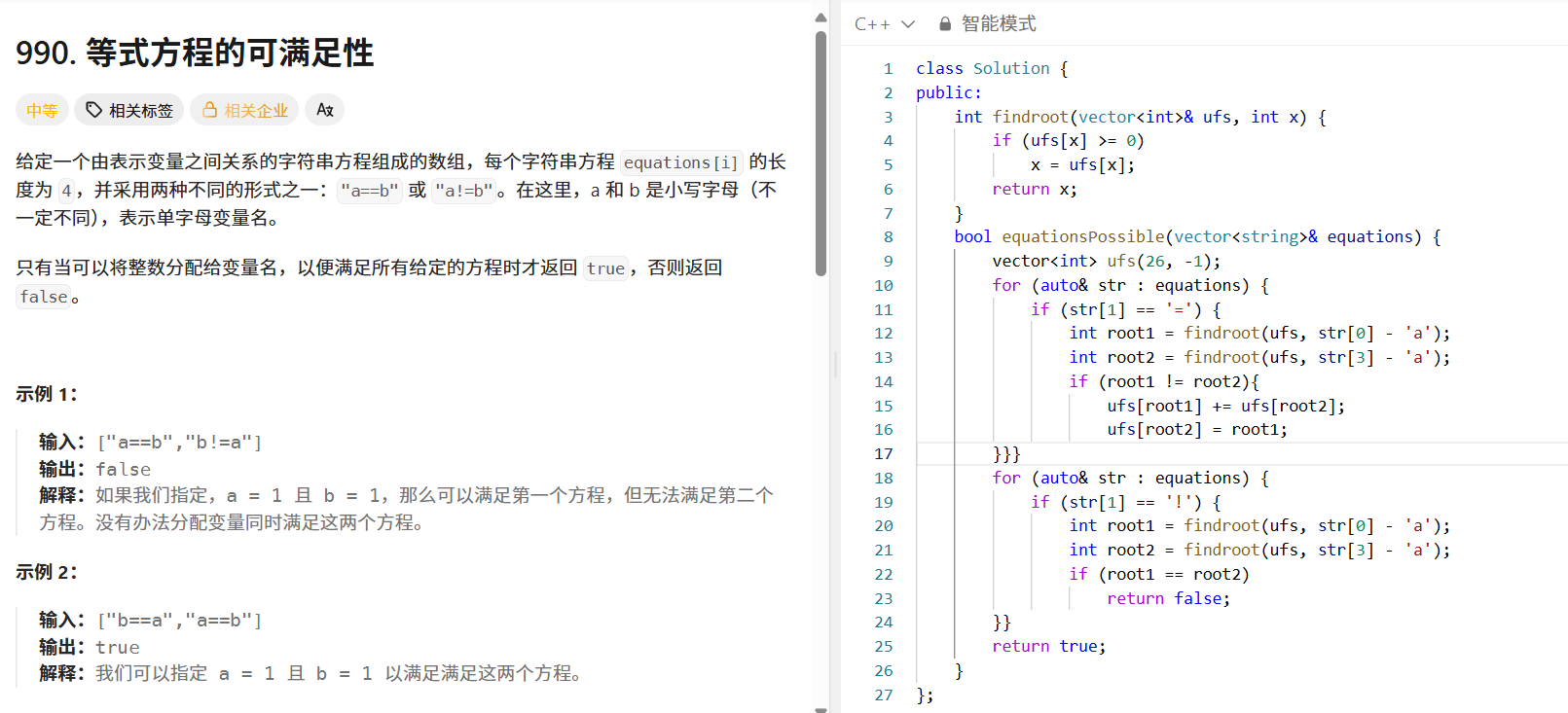
思路：

先用并查集处理所有等式，将相等的变量合并到同一集合。
再遍历所有不等式，若两个变量属于同一集合，则矛盾，返回false；否则最终返回true。

代码实现：

#include "UnionFindSet.hpp"
#include <vector>
#include <string>
using namespace std;class Solution {
public:bool equationsPossible(vector<string>& equations) {UnionFindSet ufs(26); // 26个小写字母，初始每个独立// 第一步：处理所有等式，合并相等的变量for (auto& eq : equations) {if (eq[1] == '=') {int a = eq[0] - 'a';int b = eq[3] - 'a';ufs.Union(a, b);}}// 第二步：处理所有不等式，检查是否矛盾for (auto& eq : equations) {if (eq[1] == '!') {int a = eq[0] - 'a';int b = eq[3] - 'a';if (ufs.InSet(a, b)) {return false; // 矛盾，无法满足}}}return true;}
};