当前位置：首页 > news >正文

数据结构 —— 堆

news 2025/10/27 9:58:18

一、堆(Heap)

1.堆的概念

堆（heap）：一种有特殊用途的数据结构——用来在一组变化频繁（发生增删查改的频率较高）的数据集中查找最值。

堆在物理层面上，表现为一组连续的数组区间：long[] array ；将整个数组看作是堆。

堆在逻辑结构上，一般被视为是一颗完全二叉树。

堆可分为：

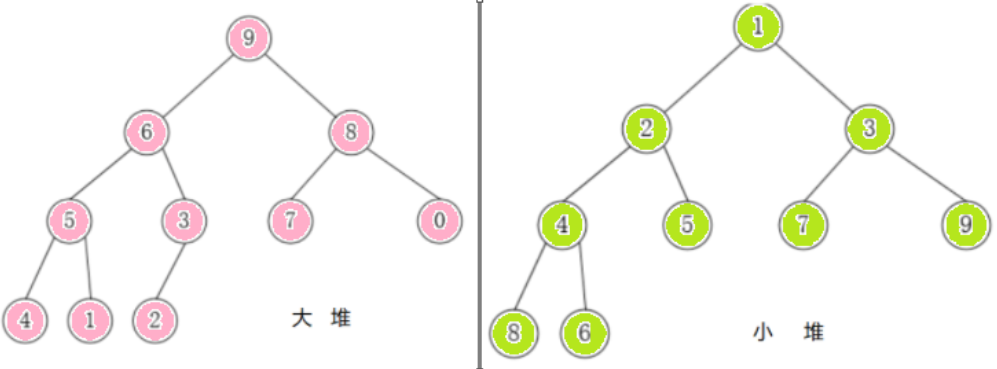
大根堆：满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆。一个堆为大根堆时，它的每一棵子树都是大根堆。

小根堆：满足任意结点的值都小于其子树中结点的值，叫做小堆，或者小根堆，或者最小堆。一个堆为小根堆时，它的每一棵子树都是小根堆。

2.堆的存储方式

堆是一棵完全二叉树，因此可以利用层序的规则进行顺序的方式来高效存储。

若假设 i 为节点在数组中的下标,则有以下规则：

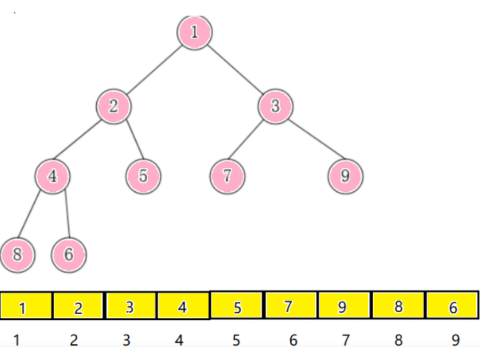
1.如果 i 为 0，则 i 表示的节点为根节点，否则 i 节点的双亲节点为(i - 1)/2;

2.如果 2*i + 1 小于节点个数，则节点 i 的左孩子的下标为 2*i + 1,否则没有左孩子；

3.如果 2*i + 2 小于节点个数，则节点 i 的右孩子的下标为 2*i + 2,否则没有有孩子。

3.堆的基本操作

堆的核心操作围绕 “维护堆特性” 展开，主要包括 堆化（Heapify）、插入（Insert）、删除堆顶（Extract Max/Min），所有操作的时间复杂度均与树的高度相关（完全二叉树高度为 log₂n，因此操作时间复杂度为 O(log n)）。

1.堆化(Heapify)：修复堆结构

堆化是堆的基础操作，指当某个节点破坏了堆特性（如父节点小于子节点）时，通过 “下沉” (向下调整)或 “上浮”(向上调整) 调整，恢复堆的正确性。分为两种场景：

向下堆化（Sift Down）：从指定节点开始，与左右子节点比较，将最大（大顶堆）的子节点与当前节点交换，重复此过程直到节点下沉到正确位置（常用于删除堆顶后修复堆）。
向上堆化（Sift Up）：从指定节点开始，与父节点比较，若当前节点更大（大顶堆）则交换，重复此过程直到节点上浮到正确位置（常用于插入新节点后修复堆）。

具体过程(以小顶堆为例)：

1️⃣. 把 parent 标记需要调整的节点，child 标记 parent 的左孩子(注意：parent 如果有孩子，则一定先是有左孩子)。

2️⃣. 如果 parent 的左孩子存在，即: child < size，进行以下操作，直到 parent 的左孩子不存在：

⏩看 parent 右孩子是否存在，若存在，找到左右孩子中最小的孩子，child 标记为两者中最小的那个；

⏩将 parent 与较小的孩子 child 比较，如果：

parent 小于 child，不做交换，调整结束；

parent 大于 child, 交换 parent 与 child，交换完成之后，目前位置的 parent 可能与它新的孩子节点不满足堆的性质，因此需要继续向下调整，即 parent = child;child = parent*2+1;然后继续2️⃣。

代码实现：

（1）向下堆化（Sift Down）代码实现（大顶堆）

// 数组存储堆，size为堆的实际大小，i为需要下沉的节点索引
public void siftDown(int[] heap, int size, int i) {while (true) {int maxIndex = i; // 初始化当前节点为最大值节点int left = 2 * i + 1; // 左子节点索引int right = 2 * i + 2; // 右子节点索引// 若左子节点存在且大于当前最大值，更新maxIndexif (left < size && heap[left] > heap[maxIndex]) {maxIndex = left;}// 若右子节点存在且大于当前最大值，更新maxIndexif (right < size && heap[right] > heap[maxIndex]) {maxIndex = right;}// 若当前节点已是最大值，无需继续下沉，退出循环if (maxIndex == i) {break;}// 交换当前节点与最大值节点swap(heap, i, maxIndex);// 继续下沉交换后的节点（原最大值节点的位置）i = maxIndex;}
}// 辅助方法：交换数组中两个索引的元素
private void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}

（2）向上堆化（Sift Up）代码实现（大顶堆）

// 数组存储堆，i为需要上浮的节点索引
public void siftUp(int[] heap, int i) {while (true) {int parentIndex = (i - 1) / 2; // 父节点索引// 若父节点不存在（当前节点是根节点）或当前节点小于等于父节点，无需继续上浮if (parentIndex < 0 || heap[i] <= heap[parentIndex]) {break;}// 交换当前节点与父节点swap(heap, i, parentIndex);// 继续上浮父节点位置的节点（原当前节点的位置）i = parentIndex;}
}

2.堆的构建

堆的构建是指将一个无序数组转换为符合堆特性的数组，核心思路是 “从最后一个非叶子节点开始，依次对每个节点执行向下堆化”（叶子节点无需调整，因为它们本身已是 “单个节点的堆”）。

构建步骤（大顶堆）

找到最后一个非叶子节点的索引：lastNonLeafIndex = (n / 2) - 1（n 为数组长度）；
从 lastNonLeafIndex 开始，向前遍历到 0，对每个节点执行向下堆化；
遍历结束后，数组即成为大顶堆。

代码实现：

// 将无序数组构建为大顶堆
public void buildMaxHeap(int[] arr) {int n = arr.length;// 从最后一个非叶子节点开始，依次向下堆化int lastNonLeafIndex = (n / 2) - 1;for (int i = lastNonLeafIndex; i >= 0; i--) {siftDown(arr, n, i);}
}

3.插入元素

插入元素的核心是 “先将新元素放到堆的末尾（数组最后一位），再通过向上堆化恢复堆特性”，确保插入后仍满足大顶堆 / 小顶堆规则。

插入步骤（大顶堆）

1️⃣. 先将元素放入到底层空间中(注意：空间不够时需要扩容)

2️⃣. 将最后新插入的节点向上调整，直到满足堆的性质；

将新元素追加到数组末尾（堆的最后一层最右侧，保持完全二叉树结构）；
对新元素（数组最后一位索引）执行向上堆化；
堆的大小 size 加 1。

代码实现：

// 向大顶堆中插入元素（假设heap数组已预留足够空间）
public void insert(int[] heap, int size, int value) {// 1. 将新元素放到堆的末尾heap[size] = value;// 2. 对新元素执行向上堆化siftUp(heap, size);// 3. 堆大小加1（实际场景中需注意数组扩容，此处简化）
}// 测试：向大顶堆 [9, 6, 8, 5, 4] 插入 7
public static void main(String[] args) {int[] heap = new int[10]; // 预留空间heap[0] = 9; heap[1] = 6; heap[2] = 8; heap[3] = 5; heap[4] = 4;int size = 5;HeapDemo demo = new HeapDemo();demo.insert(heap, size, 7);size++;System.out.println(Arrays.toString(Arrays.copyOf(heap, size))); // 输出：[9, 7, 8, 5, 4, 6]（插入后仍为大顶堆）
}

4.删除堆顶

堆顶是堆的极值（大顶堆的最大值、小顶堆的最小值），删除堆顶后需通过 “替换 + 向下堆化” 恢复堆特性，步骤如下（大顶堆为例）：

删除步骤（大顶堆）

注意：堆的删除一定删除的是堆顶元素。

1️⃣. 将堆顶元素对堆中最后一个元素交换；

2️⃣. 将堆中有效数据个数减少一个；

3️⃣. 对堆顶元素进行向下调整；

保存堆顶元素（待返回的最大值）；
将堆的最后一个元素（数组最后一位）移动到堆顶（替换堆顶，保持完全二叉树结构）；
堆的大小 size 减 1；
对新堆顶（索引 0）执行向下堆化；
返回步骤 1 保存的堆顶元素。

代码实现：

// 从大顶堆中删除并返回堆顶元素（最大值）
public int extractMax(int[] heap, int size) {// 1. 保存堆顶元素int max = heap[0];// 2. 将最后一个元素移到堆顶heap[0] = heap[size - 1];// 3. 堆大小减1size--;// 4. 对新堆顶执行向下堆化siftDown(heap, size, 0);// 5. 返回最大值return max;
}// 测试：删除大顶堆 [9, 7, 8, 5, 4, 6] 的堆顶
public static void main(String[] args) {int[] heap = {9, 7, 8, 5, 4, 6};int size = 6;HeapDemo demo = new HeapDemo();int max = demo.extractMax(heap, size);size--;System.out.println("删除的最大值：" + max); // 输出：9System.out.println("删除后的堆：" + Arrays.toString(Arrays.copyOf(heap, size))); // 输出：[8, 7, 6, 5, 4]（仍为大顶堆）
}

4.堆的时间复杂度分析

堆的所有核心操作均与完全二叉树的高度相关，而完全二叉树的高度 h = log₂n（n 为节点数），因此各操作的时间复杂度如下：

操作	时间复杂度	分析
向下堆化	O(log n)	最坏情况需从根节点下沉到叶子节点，共 `h`次交换和比较，`h = log₂n`
向上堆化	O(log n)	最坏情况需从叶子节点上浮到根节点，共 `h`次交换和比较，`h = log₂n`
堆的构建	O(n)	表面看是 “n/2 次向下堆化”，但底层节点的堆化次数少，数学推导总复杂度为 O (n)
插入元素	O(log n)	仅需一次向上堆化，复杂度为 O (log n)
删除堆顶	O(log n)	仅需一次向下堆化，复杂度为 O (log n)

5.堆的经典应用场景

1. 优先队列（Priority Queue）

优先队列是堆最直接的应用，它的核心需求是 “每次取出优先级最高的元素”（如任务调度中优先执行高优先级任务）。

Java 中的 PriorityQueue 底层就是小顶堆（默认），可通过传入 Comparator 改为大顶堆；
优先队列的 offer()（插入）和 poll()（删除队首）操作，本质就是堆的插入和删除堆顶操作，时间复杂度 O (log n)。

Java PriorityQueue 示例（大顶堆）

// 初始化大顶堆（通过Comparator指定排序规则）
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);// 插入元素（offer() = 堆的insert）
maxHeap.offer(5);
maxHeap.offer(3);
maxHeap.offer(8);
maxHeap.offer(1);// 删除并获取堆顶（poll() = 堆的extractMax）
while (!maxHeap.isEmpty()) {System.out.print(maxHeap.poll() + " "); // 输出：8 5 3 1（按优先级从高到低）
}

2.堆排序（Heap Sort）

堆排序是一种基于堆的排序算法，核心思路是 “利用大顶堆的堆顶是最大值” 的特性，逐步将最大值放到数组末尾，最终得到有序数组。

堆排序步骤：

1. 将无序数组构建为大顶堆；

2. 交换堆顶（最大值）与数组最后一位元素，此时最大值已 “归位”；

3. 对前 n-1 个元素执行向下堆化，恢复大顶堆；

4. 重复步骤 2-3，直到所有元素归位。

堆排序的时间复杂度为 O (n log n)，空间复杂度为 O (1)（原地排序），但不稳定（相同元素的相对位置可能变化）。

public void heapSort(int[] arr) {int n = arr.length;// 步骤1：构建大顶堆buildMaxHeap(arr);// 步骤2-3：逐步将最大值归位并恢复堆for (int i = n - 1; i > 0; i--) {// 交换堆顶（最大值）与当前未排序部分的最后一位swap(arr, 0, i);// 对前i个元素（未排序部分）执行向下堆化siftDown(arr, i, 0);}
}// 测试：对无序数组 [4, 6, 8, 5, 9] 进行堆排序
public static void main(String[] args) {int[] arr = {4, 6, 8, 5, 9};HeapDemo demo = new HeapDemo();demo.heapSort(arr);System.out.println(Arrays.toString(arr)); // 输出：[4, 5, 6, 8, 9]（升序）
}

3.Top-K 问题（获取前 K 个最大 / 最小元素）

Top-K 问题是高频面试题（如 “从 100 万个数中找出前 10 个最大的数”），用堆解决可大幅优化性能，避免全量排序（全量排序复杂度 O (n log n)，堆解法复杂度 O (n log K)）。

解决思路（找前 K 个最大元素）：

1. 用数组的前 K 个元素构建小顶堆（堆顶是当前 K 个元素中的最小值）；
2. 遍历数组剩余元素，若元素大于堆顶，则替换堆顶，并执行向下堆化；
3. 遍历结束后，小顶堆中的 K 个元素就是前 K 个最大元素。

优势：仅需维护大小为 K 的堆，内存占用低，适合大数据量场景。

Top-K 问题代码实现（找前 3 个最大元素）：

public int[] findTopK(int[] arr, int k) {if (k <= 0 || k > arr.length) {throw new IllegalArgumentException("K值无效");}// 步骤1：用前K个元素构建小顶堆int[] heap = new int[k];System.arraycopy(arr, 0, heap, 0, k);// 构建小顶堆（修改siftDown为“父节点小于等于子节点”）buildMinHeap(heap);// 步骤2：遍历剩余元素，更新小顶堆for (int i = k; i < arr.length; i++) {if (arr[i] > heap[0]) { // 若当前元素大于堆顶（小顶堆的最小值）heap[0] = arr[i];siftDownMin(heap, k, 0); // 向下堆化（小顶堆版）}}return heap;
}// 构建小顶堆（参考大顶堆，仅修改比较逻辑）
private void buildMinHeap(int[] arr) {int n = arr.length;int lastNonLeafIndex = (n / 2) - 1;for (int i = lastNonLeafIndex; i >= 0; i--) {siftDownMin(arr, n, i);}
}// 小顶堆的向下堆化（父节点小于等于子节点）
private void siftDownMin(int[] heap, int size, int i) {while (true) {int minIndex = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < size && heap[left] < heap[minIndex]) {minIndex = left;}if (right < size && heap[right] < heap[minIndex]) {minIndex = right;}if (minIndex == i) break;swap(heap, i, minIndex);i = minIndex;}
}// 测试：从 [3, 1, 4, 1, 5, 9, 2, 6] 中找前3个最大元素
public static void main(String[] args) {int[] arr = {3, 1, 4, 1, 5, 9, 2, 6};HeapDemo demo = new HeapDemo();int[] top3 = demo.findTopK(arr, 3);System.out.println(Arrays.toString(top3)); // 输出：[5, 6, 9]（小顶堆形式，排序后为[9,6,5]）
}

6.堆的常见问题和注意事项

堆与二叉搜索树（BST）的区别：

- 堆是 “完全二叉树”，仅保证父子节点的优先级关系，不保证左右子树的大小关系；
- BST 是 “任意二叉树”，保证左子树所有节点小于根节点，右子树所有节点大于根节点，可通过中序遍历得到有序序列；
- 堆的优势是 “快速获取极值”（O (log n)），BST 的优势是 “有序查找 / 插入 / 删除”（平衡 BST 如红黑树，复杂度 O (log n)）。

堆的稳定性：堆是不稳定的数据结构，因为在堆化过程中，相同值的节点可能会交换位置（如堆排序中，相同元素的相对位置会变化）。
堆的扩容：若用数组存储堆，当元素数量超过数组长度时，需手动扩容（如 Java 的ArrayList一样，创建新数组并复制元素），扩容时间复杂度为 O (n)，但属于低频操作，不影响堆的整体性能。
小顶堆与大顶堆的选择：