MATLAB基于灰靶决策模型的高校信息化设备供应商选择研究
一、 引言
研究背景与意义:
背景:高校信息化建设是推动教育现代化的重要引擎,而设备采购是其中的关键环节。供应商的选择直接关系到项目投资效益、设备运行稳定性与后期服务保障。
问题提出:供应商选择是一个典型的多属性群决策问题,指标间存在矛盾性(如价格低往往与技术新矛盾),且信息具有灰色性(如企业信誉、服务响应速度难以精确量化)。
研究意义:引入灰靶决策模型,能够将定性判断与定量分析相结合,在信息不完全的情况下,科学、客观地遴选出最优供应商,降低采购风险,提升资金使用效率。
文献综述:
回顾供应商选择方法(如招标法、成本法、线性加权法、模糊综合评价法、数据包络分析法等)的优缺点。
综述灰靶决策理论在供应链管理、物流供应商选择等领域的研究进展。
指出当前研究在高校这一特定领域,尤其是在信息化设备采购这一具体场景中的应用尚不充分,从而确立本研究的立足点和创新性。
二、 高校信息化设备供应商评价指标体系构建
构建原则:系统性、科学性、可操作性、定性与定量相结合。
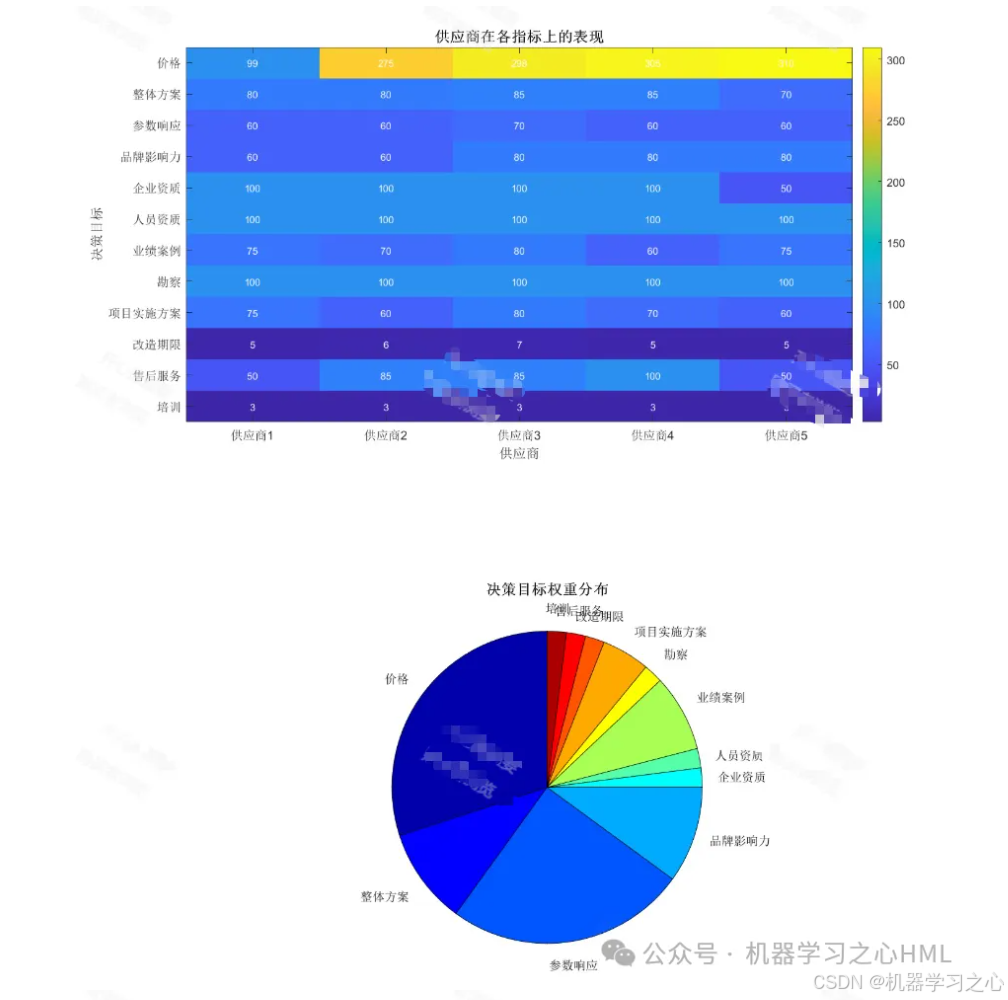
指标体系(示例):
二级指标:产品报价(成本型)、生命周期成本(成本型)、付款方式灵活性(效益型)
二级指标:企业规模与行业地位(效益型)、过往成功案例(效益型)、合同履约率(效益型)
二级指标:售后服务响应时间(成本型)、技术培训支持力度(效益型)、备件供应能力(效益型)
二级指标:研发投入占比(效益型)、技术方案成熟度(效益型)、与现有系统兼容性(效益型)
二级指标:产品合格率(效益型)、产品性能先进性(效益型)、平均无故障时间(效益型)
一级指标B1:产品质量
一级指标B2:技术能力
一级指标B3:服务水平
一级指标B4:企业资质与信誉
一级指标B5:成本效益
三、 基于组合赋权-灰靶决策的供应商选择模型
阶段一:确定指标组合权重
主观权重(α):采用层次分析法(AHP)。邀请高校信息中心、财务处、使用院系的专家组成决策小组,通过两两比较判断矩阵,计算得出主观权重向量α。
客观权重(β):采用熵权法。根据各候选供应商在所有指标上的原始数据,计算其信息熵,从而确定客观权重向量β。熵权法能有效放大指标数据的差异程度。
组合权重(W):为平衡主观偏好与客观数据,采用线性加权法计算综合权重:
W = θ * α + (1-θ) * β
。其中θ(0≤θ≤1)为偏好系数,可由决策者根据实际情况设定(如θ=0.5表示主客观同等重要)。
阶段二:灰靶决策模型构建与求解
构造决策矩阵:设有m个候选供应商,n个评价指标,构造初始决策矩阵
A = (a_ij)_{m×n}
。
数据标准化(无量纲化):
对效益型指标(越大越好):
b_ij = [a_ij - min(a_j)] / [max(a_j) - min(a_j)]
对成本型指标(越小越好):
b_ij = [max(a_j) - a_ij] / [max(a_j) - min(a_j)]
得到标准化矩阵
B = (b_ij)_{m×n}
。
确定靶心(理想供应商):
从标准化矩阵B的每一列中选取最优值,构成靶心向量B0。
B0 = (b_01, b_02, …, b_0n) = (max(b_i1), max(b_i2), …, max(b_in))
。(对于成本型指标,标准化后已转化为效益型,故统一取最大值)。
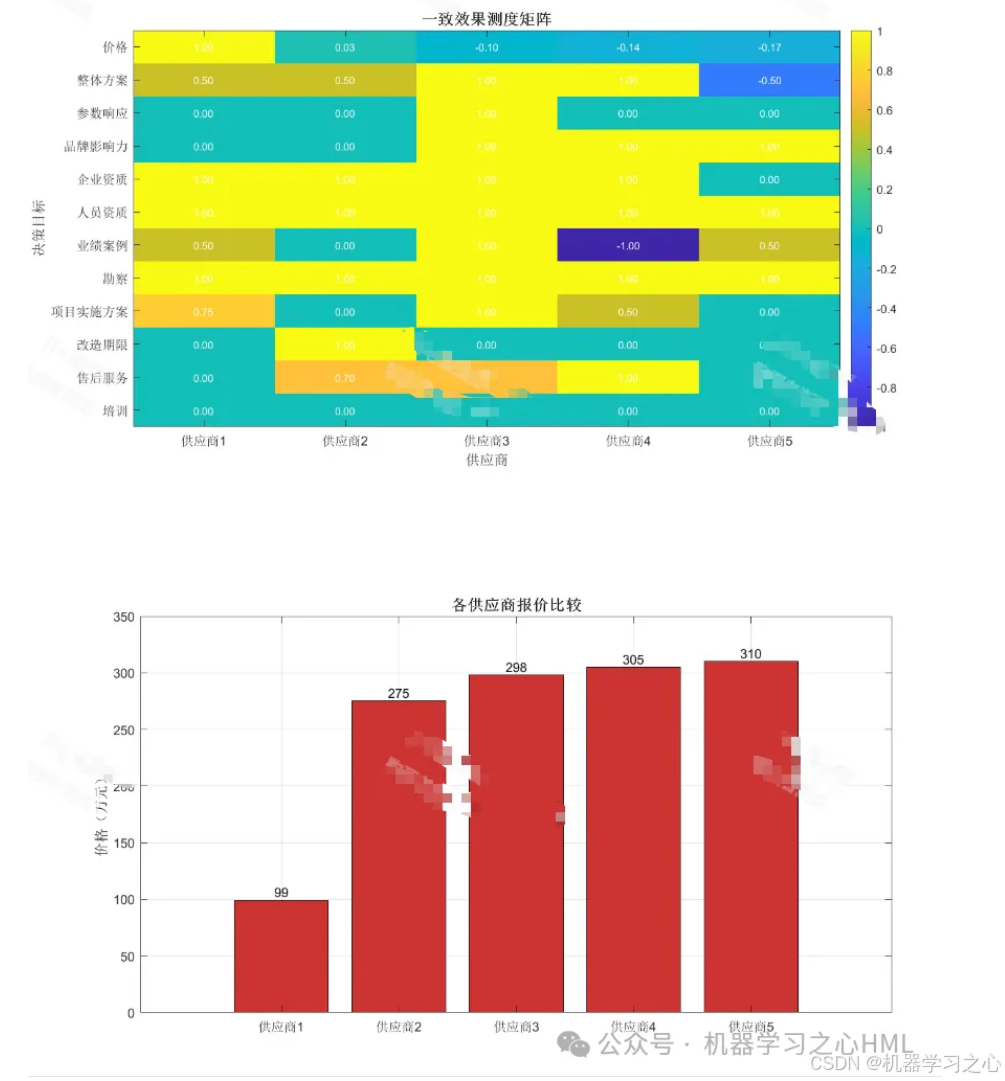
计算加权靶心度:
计算关联系数:计算各供应商与靶心在每个指标上的关联系数
ξ_i(j)
。
ξ_i(j) = (min_min |b_0j - b_ij| + ρ * max_max |b_0j - b_ij|) / (|b_0j - b_ij| + ρ * max_max |b_0j - b_ij|)
其中,
ρ
为分辨系数,通常取0.5。
计算加权靶心度:利用阶段一求得的组合权重W,计算每个供应商的综合靶心度
γ_i
。
γ_i = Σ (w_j * ξ_i(j))
,其中
j=1 to n
。
γ_i
的取值范围为(0, 1],其值越大,表示该供应商与理想供应商越接近,综合表现越优。
四、 实例分析
场景设定:假设某高校计划采购一批核心网络交换机,现有4家供应商(S1, S2, S3, S4)通过初选。
数据收集与处理:
收集4家供应商在上述指标体系下的原始数据(部分定性指标通过专家打分量化)。
按照阶段一的方法,计算主、客观及组合权重。例如,计算得出组合权重W = (0.15, 0.20, 0.25, 0.25, 0.15) [对应5个一级指标]。
模型运算:
假设计算结果为:
γ_S1 = 0.85
,
γ_S2 = 0.72
,
γ_S3 = 0.65
,
γ_S4 = 0.78
。
对原始数据进行标准化。
确定靶心向量B0。
计算各供应商与B0的关联系数矩阵。
结合权重W,计算各供应商的最终靶心度
γ_i
。
结果分析与决策:
排序选择:根据靶心度排序为 S1 > S4 > S2 > S3。因此,供应商S1为最优选择。
方法对比:将本模型结果与单纯使用AHP加权求和法或价格最低法得到的结果进行对比,分析差异原因,凸显灰靶模型在综合权衡和处理灰色信息方面的优势。
敏感性分析:改变偏好系数θ,观察组合权重和最终排序是否稳定,验证模型的鲁棒性。
五、 结论与展望
研究结论:
本研究成功将灰靶决策模型应用于高校信息化设备供应商选择,构建了一套科学的评价与决策流程。
通过组合赋权,有效融合了决策者的主观经验和指标数据的客观信息,使权重设定更为合理。
实例证明,该模型逻辑清晰,计算简便,结果直观,具有很高的实用价值和推广潜力。
不足与展望:
指标体系的普适性与特定项目(如软件采购、硬件采购)的个性化需求之间可能存在矛盾,未来可研究动态指标体系。
可考虑将模型与采购管理系统集成,开发成辅助决策支持模块,实现智能化评选。
未来可引入更复杂的权重模型(如博弈论组合赋权)或与其他决策方法(如TOPSIS, VIKOR)进行对比融合研究。
