MATLAB基于博弈论组合赋权灰靶模型的煤矿安全综合评价
一、 引言
研究背景与意义:
背景:煤矿安全生产事关重大,但其系统复杂、致灾因素多,是一个典型的灰色系统(信息不完全、不确定)。
问题提出:传统安全评价方法(如安全检查表、LEC法、模糊综合评价)在权重确定上,或过于主观(专家打分),或过于机械(纯数据驱动),难以兼顾决策者意图与数据内在规律。
研究意义:博弈论组合赋权旨在寻求主客观权重的最优均衡,灰靶模型善于在“贫信息”下进行优劣排序。二者结合,为煤矿安全状态的精准诊断和动态评价提供了创新性解决方案。
文献综述:
综述煤矿安全评价方法的发展(从定性到定量,从单一到综合)。
综述权重确定方法的研究(主观法、客观法及组合赋权法),指出简单线性组合的不足,引出博弈论组合赋权的优越性。
综述灰靶理论在安全、风险评价领域的应用,指出其处理不确定性的潜力。
总结:明确提出将“博弈论组合赋权”与“灰靶模型”进行深度融合,应用于煤矿安全综合评价,是本研究的创新点。
二、 理论基础与模型构建
- 煤矿安全评价指标体系构建
原则:科学性、系统性、可操作性、动态性。
体系结构(示例):
A1:人员安全素质 (U1)
A2:设备安全状态 (U2)
A3:环境安全状况 (U3)
A4:安全管理效能 (U4)
二级指标:安全培训合格率(效益型),违章作业率(成本型),特种作业持证率(效益型)
二级指标:设备完好率(效益型),安全防护装置完好率(效益型),故障停机率(成本型)
二级指标:瓦斯浓度超限次数(成本型),粉尘合格率(效益型),顶板支护合格率(效益型)
二级指标:安全投入强度(效益型),应急预案完备率(效益型),事故隐患排查率(效益型)
一级指标(类别):
- 博弈论组合赋权模型
步骤1:计算基础权重向量
设共有
n
个评价指标。
主观权重向量
α
:使用AHP法,通过专家评判矩阵计算得出。
α = (α1, α2, …, αn)
。
客观权重向量
β
:使用熵权法,根据各煤矿的指标原始数据计算得出。
β = (β1, β2, …, βn)
。
步骤2:构建组合权重模型
设组合权重为:
W = λ1 * α + λ2 * β
,其中
λ1
和
λ2
为线性组合系数,且
λ1 + λ2 = 1
。
博弈论的思想是寻找
λ1
和
λ2
,使
W
与
α
和
β
的离差极小化,即寻求一种“一致”或“妥协”。
步骤3:求解最优组合系数
根据博弈论模型,转化为最优化问题,目标函数为:
min || W - α ||^2 + || W - β ||^2
代入
W = λ1 * α + λ2 * β
,并根据一阶导数条件,可得到如下线性方程组:
text
[ α·α α·β ] [λ1] [α·α] [ ] [ ] = [ ] [ α·β β·β ] [λ2] [β·α]
(其中
·
表示向量的内积)
解出
λ1*
和
λ2*
,并进行归一化处理:
λ1’ = λ1* / (λ1* + λ2*)
,
λ2’ = λ2* / (λ1* + λ2*)
。
步骤4:计算最优组合权重
W* = λ1’ * α + λ2’ * β
。此权重
W*
即为主客观信息博弈均衡后的最优权重。
- 加权灰靶决策模型
步骤1:构造初始决策矩阵
假设有
m
个待评价煤矿(或同一煤矿
m
个不同时期),
n
个指标。构造矩阵
A = (a_ij)_{m×n}
。
步骤2:数据无量纲化(灰靶变换)
针对效益型(越大越好)和成本型(越小越好)指标,分别采用相应的公式进行标准化处理,得到标准矩阵
B = (b_ij)_{m×n}
。
步骤3:确定靶心(标准模式)
从标准矩阵
B
的每一列中选取最优值,构成靶心向量
B0 = (b_01, b_02, …, b_0n)
。
效益型取最大值,成本型取最小值。
步骤4:计算加权靶心度
传统的灰靶模型计算关联系数后求平均。此处引入组合权重
W*
,计算加权综合靶心度。
首先,计算各方案(煤矿)与靶心在各指标上的关联系数
ξ_i(j)
。
然后,计算加权靶心度
γ_i
:
γ_i = Σ [ w_j * ξ_i(j) ]
,其中
j=1 to n
,
w_j
为第
j
个指标的组合权重。
γ_i
越接近1,说明该煤矿的安全状态越接近理想最优水平。
三、 实例分析
数据收集:选取5个典型煤矿(A, B, C, D, E)或同一煤矿连续5年的数据。
权重计算:
邀请专家,通过AHP法计算得到主观权重
α
。
收集原始数据,通过熵权法计算得到客观权重
β
。
运用博弈论模型,求解最优组合系数
λ1’
和
λ2’
,并计算最终组合权重
W*
。
灰靶评价:
将原始数据标准化,确定靶心
B0
。
计算各煤矿与靶心的关联系数矩阵。
利用组合权重
W*
,计算各煤矿的加权靶心度
γ_i
。
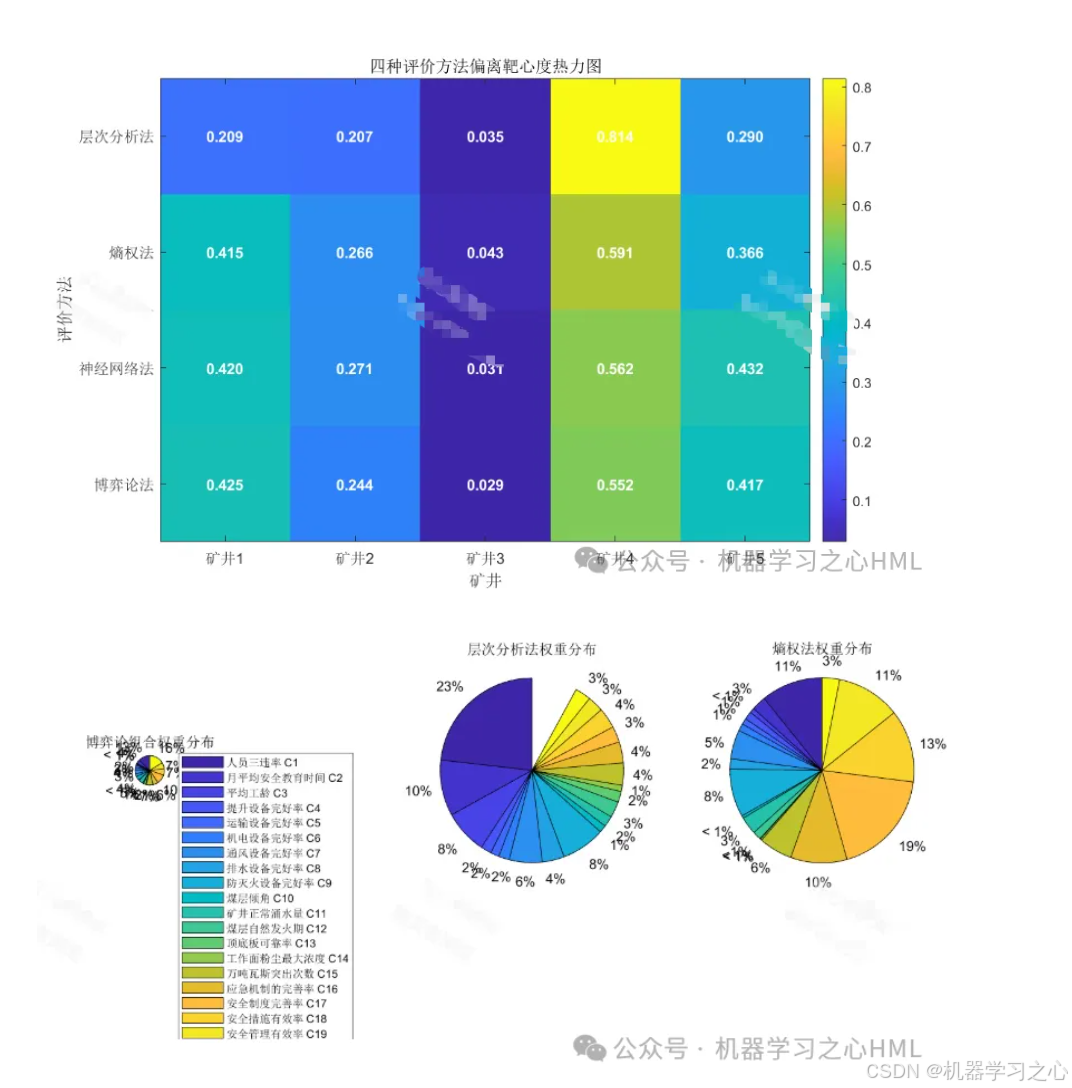
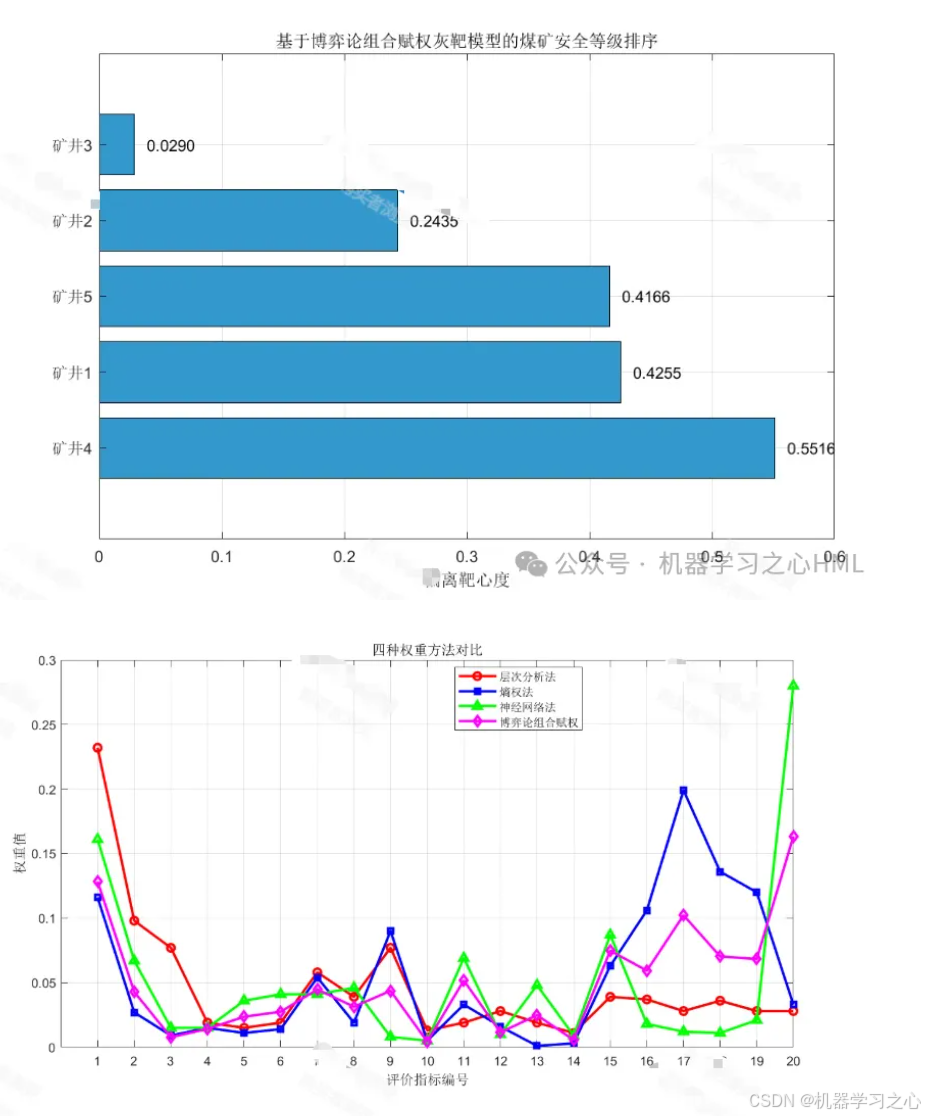
结果与分析:
排序与分级:根据
γ_i
对5个煤矿进行安全状况排序。可设定阈值,如:
γ>0.8
(优秀),
0.6<γ≤0.8
(良好),
γ≤0.6
(待改进)。
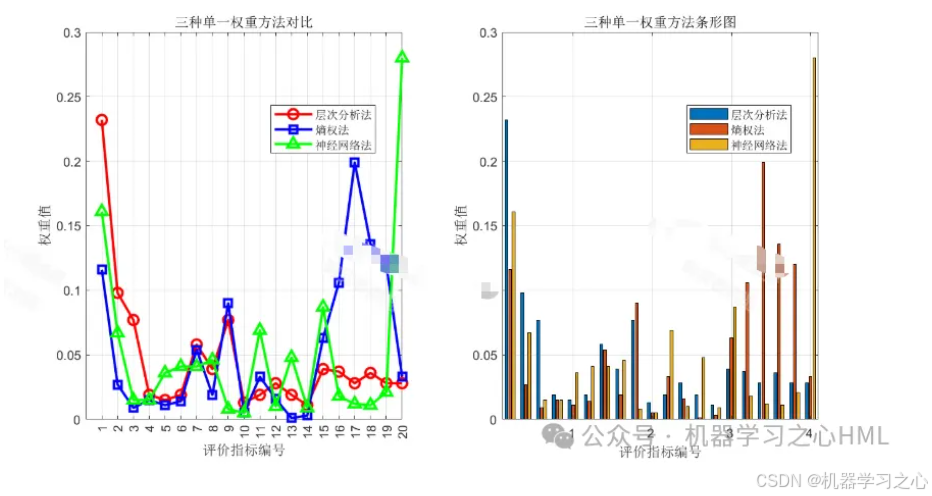
方法对比:将本模型(博弈论组合赋权-灰靶)的评价结果与单一AHP-灰靶、单一熵权-灰靶模型的评价结果进行对比,分析排序差异,论证组合赋权模型的优越性和稳定性。
诊断分析:对于靶心度低的煤矿,分析其在不同一级指标(人、机、环、管)上的得分情况,找出安全管理的薄弱环节,为制定针对性整改措施提供精确依据。
四、 结论与展望
研究结论:
构建的博弈论组合赋权灰靶模型,成功地实现了煤矿安全评价中主客观信息的集成与均衡,权重设定更为科学。
灰靶模型有效处理了安全信息的不确定性和灰色性,评价结果直观(靶心度),具有良好的区分度和诊断功能。
实例证明,该模型在煤矿安全综合评价中是可行、有效且优越的,是一种科学的辅助决策工具。
不足与展望:
指标体系的构建可以进一步动态化,纳入实时监测数据。
博弈论模型可以考虑更多种基础权重方法(如CRITIC法、离差最大化法等)进行组合。
未来可将该模型与GIS、BIM或数字孪生技术结合,开发智能化的煤矿安全动态评价与预警平台。
