链表-循环双向链表【node4】

基本结构

循环双向链表中的每个节点包含三部分：数据域、前向指针域和后向指针域。

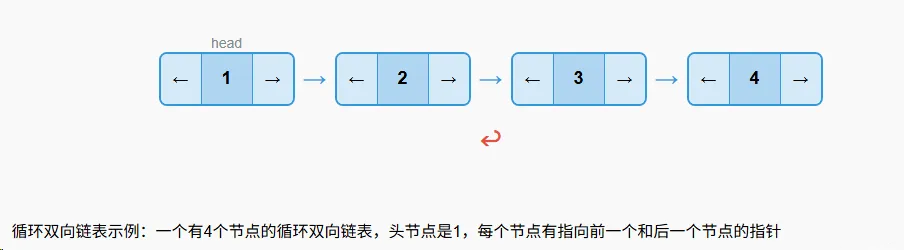
// 循环双向链表的节点内部类
static class DoublyNode {double data;       // 支持整数/小数（适配原代码测试数据）DoublyNode next;   // 指向下一个节点的引用DoublyNode prev;   // 指向前一个节点的引用// 节点构造方法public DoublyNode(double data) {this.data = data;this.next = null;this.prev = null;}
}private DoublyNode head;  // 链表头节点（唯一入口，尾节点通过head.prev获取）// 循环双向链表构造方法（初始化空链表）
public CircularDoublyLinkedList() {this.head = null;
}

遍历

循环双向链表可以进行正向和反向遍历。

正向遍历

算法步骤

1. 如果链表为空（head为None），则返回空列表
2. 初始化一个结果列表，并设置当前指针current为head
3. 将当前节点的数据添加到结果列表中
4. 移动当前指针到下一个节点(current = current.next)
5. 如果当前指针不等于头节点，重复步骤3和4
6. 返回结果列表

/*** 正向遍历链表（从头→尾）* @return 存储节点数据的List集合*/
public List<Double> traverse() {List<Double> result = new ArrayList<>();if (head == null) {return result;}// 采用do-while逻辑：先添加头节点，再循环遍历后续节点DoublyNode current = head;result.add(current.data);current = current.next;// 指针回到头节点时停止（循环链表闭环特性）while (current != head) {result.add(current.data);current = current.next;}return result;
}

反向遍历

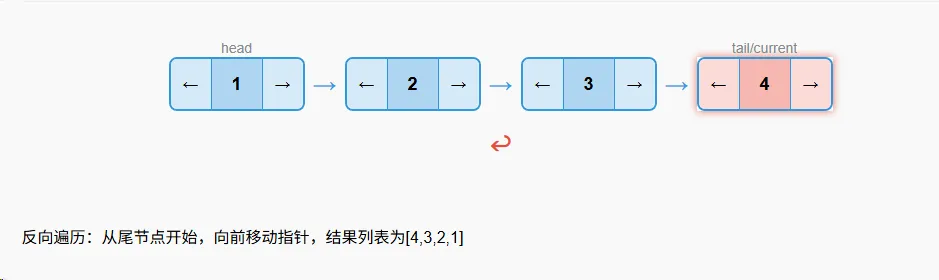
算法**步骤**

1. 如果链表为空（head为None），则返回空列表
2. 初始化一个结果列表，并设置当前指针current为尾节点(head.prev)
3. 将当前节点的数据添加到结果列表中
4. 移动当前指针到前一个节点(current = current.prev)
5. 如果当前指针不等于尾节点，重复步骤3和4
6. 返回结果列表

/*** 反向遍历链表（从尾→头）* @return 存储节点数据的List集合*/
public List<Double> reverseTraverse() {List<Double> result = new ArrayList<>();if (head == null) {return result;}// 尾节点 = 头节点的prev，从尾节点开始遍历DoublyNode current = head.prev;result.add(current.data);current = current.prev;// 指针回到尾节点时停止while (current != head.prev) {result.add(current.data);current = current.prev;}return result;
}

插入

空链表插入

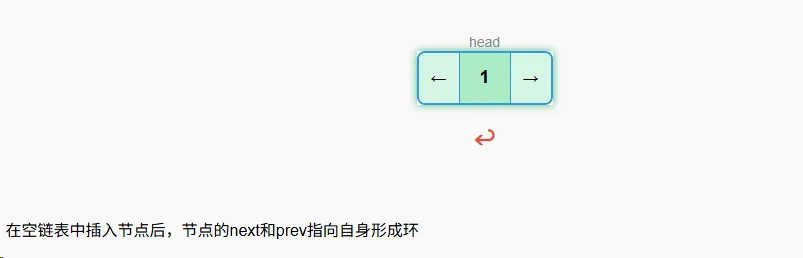
算法

1. 创建新节点
2. 将头指针指向新节点
3. 将新节点的next和prev都指向自身，形成环

/*** 空链表专用：插入第一个节点（形成自闭环）* @param data 节点数据* @return 插入成功返回true*/
private boolean insertEmpty(double data) {DoublyNode newNode = new DoublyNode(data);head = newNode;// 自闭环：节点的next和prev都指向自身newNode.next = newNode;newNode.prev = newNode;return true;
}

尾部插入

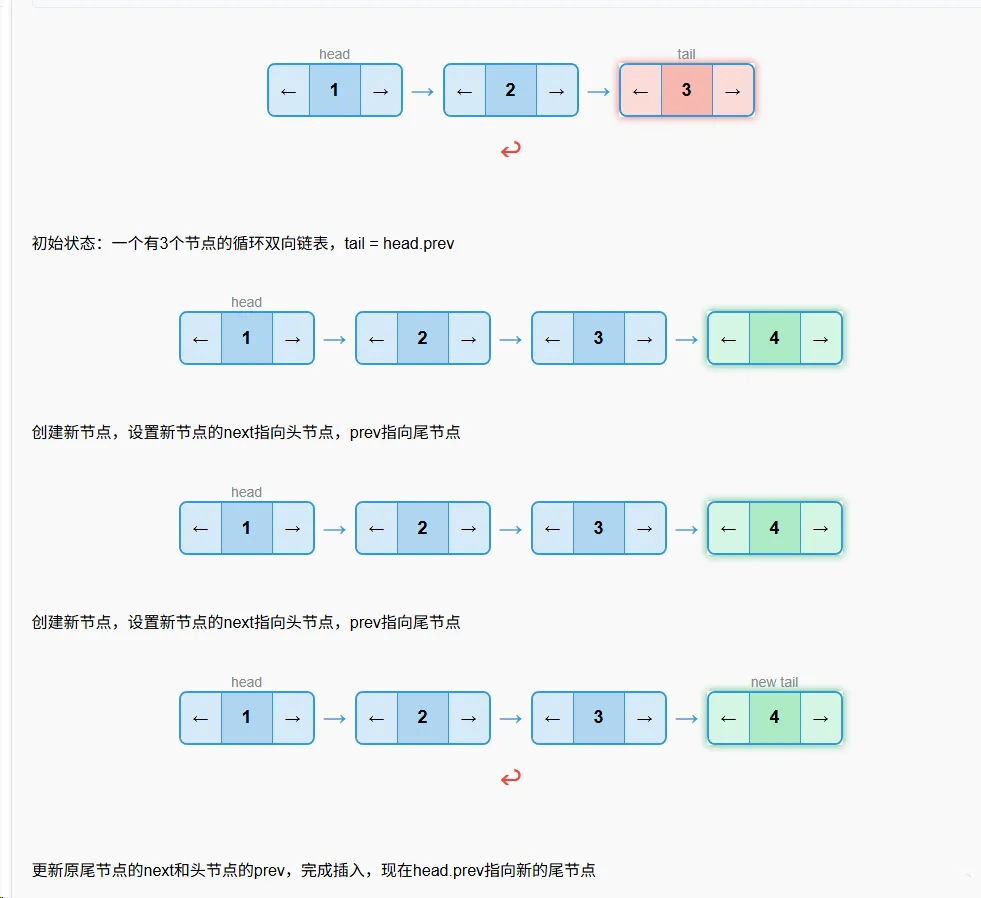
算法步骤

1. 如果链表为空，调用insert_empty方法
2. 创建新节点
3. 获取当前尾节点(head.prev)
4. 设置新节点的next指向头节点，prev指向尾节点
5. 更新原尾节点的next指向新节点
6. 更新头节点的prev指向新节点

/*** 尾插法：在链表尾部插入节点* @param data 节点数据* @return 插入成功返回true*/
public boolean append(double data) {// 空链表直接调用专用插入方法if (head == null) {return insertEmpty(data);}DoublyNode newNode = new DoublyNode(data);DoublyNode tail = head.prev;  // 快速获取尾节点（无需遍历）// 1. 新节点建立双向连接：prev连尾节点，next连头节点（维持闭环）newNode.prev = tail;newNode.next = head;// 2. 更新原尾节点和头节点的连接tail.next = newNode;head.prev = newNode;return true;
}

头部插入

算法步骤

1. 先在尾部添加节点(使用append方法)
2. 更新头指针指向新添加的节点(head = head.prev)

/**
* 头插法：在链表头部插入节点
* @param data 节点数据
* @return 插入成功返回true
*/
public boolean prepend(double data) {// 复用append逻辑：先插入到尾部，再将头节点指向新节点（原尾部）append(data);head = head.prev;  // 新节点是原尾部，head.prev指向它return true;
}

在指定数据的节点后插入新节点

/*** 在指定数据的节点后插入新节点* @param targetData 目标节点的数据* @param data 新节点的数据* @return 插入成功返回true，失败返回false*/
public boolean insertAfter(double targetData, double data) {if (head == null) {return false;}DoublyNode current = head;// 循环查找目标节点（遍历闭环）while (true) {if (current.data == targetData) {// 找到目标节点，执行双向插入DoublyNode newNode = new DoublyNode(data);// 1. 新节点连接：prev连目标节点，next连目标节点的原后继newNode.prev = current;newNode.next = current.next;// 2. 原后继节点的prev指向新节点current.next.prev = newNode;// 3. 目标节点的next指向新节点current.next = newNode;return true;}current = current.next;// 指针回到头节点 → 遍历完成未找到目标if (current == head) {break;}}return false;
}

在指定数据的节点前插入新节点

/*** 在指定数据的节点前插入新节点* @param targetData 目标节点的数据* @param data 新节点的数据* @return 插入成功返回true，失败返回false*/
public boolean insertBefore(double targetData, double data) {if (head == null) {return false;}// 目标是头节点 → 直接复用prepend（头插法）if (head.data == targetData) {return prepend(data);}// 从第二个节点开始查找（避免重复检查头节点）DoublyNode current = head.next;// 遍历到回到头节点为止while (current != head) {if (current.data == targetData) {// 找到目标节点，执行双向插入DoublyNode newNode = new DoublyNode(data);// 1. 新节点连接：prev连目标节点的原前驱，next连目标节点newNode.prev = current.prev;newNode.next = current;// 2. 原前驱节点的next指向新节点current.prev.next = newNode;// 3. 目标节点的prev指向新节点current.prev = newNode;return true;}current = current.next;}return false;  // 未找到目标节点
}

删除

头节点删除

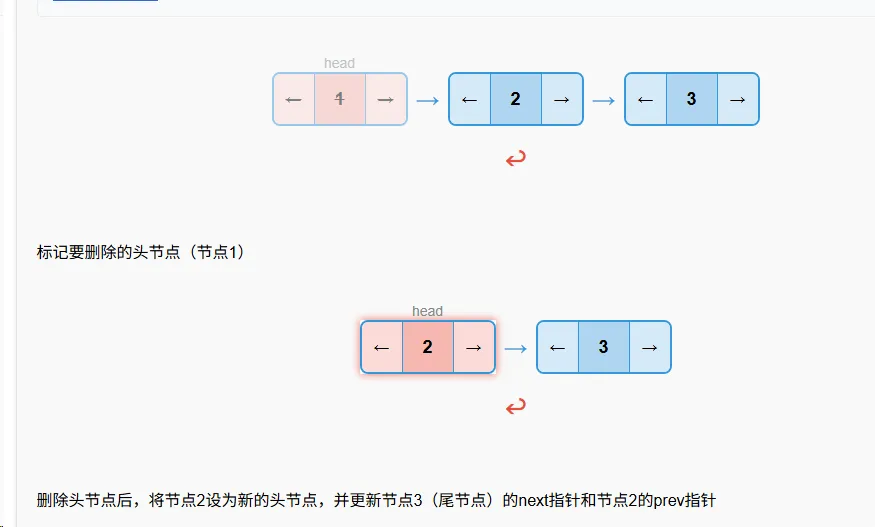
算法步骤

1. 如果链表为空，返回失败
2. 如果链表只有一个节点，则删除该节点并将head设为None
3. 保存当前头节点，尾节点和新头节点的引用
4. 更新尾节点的next指向新头节点
5. 更新新头节点的prev指向尾节点
6. 更新头指针指向新头节点

/*** 删除头节点* @return 删除成功返回true，失败返回false*/
public boolean deleteHead() {if (head == null) {return false;}// 单节点链表 → 调用专用删除方法if (head.next == head) {return deleteOnlyNode();}DoublyNode oldHead = head;DoublyNode tail = oldHead.prev;    // 尾节点DoublyNode newHead = oldHead.next; // 新头节点（原头节点的后继）// 1. 尾节点与新头节点建立双向连接（跳过原头节点）tail.next = newHead;newHead.prev = tail;// 2. 更新头节点为新头节点head = newHead;return true;
}

尾节点删除

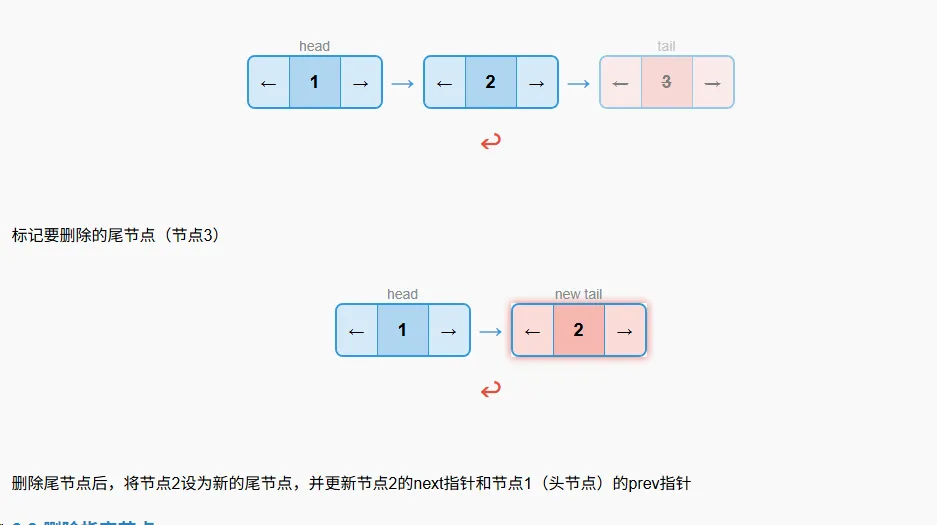
算法步骤

1. 如果链表为空，返回失败
2. 如果链表只有一个节点，则删除该节点并将head设为None
3. 获取当前尾节点和新尾节点（当前尾节点的前一个节点）
4. 更新新尾节点的next指向头节点
5. 更新头节点的prev指向新尾节点

/*** 删除尾节点* @return 删除成功返回true，失败返回false*/
public boolean deleteTail() {if (head == null) {return false;}// 单节点链表 → 调用专用删除方法if (head.next == head) {return deleteOnlyNode();}DoublyNode oldTail = head.prev;    // 原尾节点DoublyNode newTail = oldTail.prev; // 新尾节点（原尾节点的前驱）// 1. 新尾节点与头节点建立双向连接（跳过原尾节点）newTail.next = head;head.prev = newTail;return true;
}

指定节点删除

算法步骤

1. 如果链表为空，返回失败
2. 遍历链表查找目标节点
3. 如果找到目标节点：
   1. 如果目标节点是头节点，调用delete_head方法
   2. 如果目标节点是尾节点，调用delete_tail方法
   3. 否则，更新目标节点前后节点的连接，删除目标节点

/*** 删除指定数据的节点（支持头/尾/中间节点）* @param data 要删除的节点数据* @return 删除成功返回true，失败返回false*/
public boolean delete(double data) {if (head == null) {return false;}// 1. 单节点链表且匹配数据 → 删除唯一节点if (head.next == head && head.data == data) {return deleteOnlyNode();}// 2. 目标是头节点 → 复用deleteHeadif (head.data == data) {return deleteHead();}// 3. 目标是尾节点 → 复用deleteTailif (head.prev.data == data) {return deleteTail();}// 4. 查找中间节点（从第二个节点到倒数第二个节点）DoublyNode current = head.next;while (current != head.prev) {if (current.data == data) {// 双向跳过当前节点：前驱连后继，后继连前驱current.prev.next = current.next;current.next.prev = current.prev;return true;}current = current.next;}return false;  // 未找到目标节点
}

查找

算法步骤

1. 如果链表为空，返回None
2. 遍历链表查找目标节点
3. 如果找到目标节点，返回该节点
4. 如果遍历完整个链表都没有找到，返回None

正向查找指定数据的节点（从头→尾）

/*** 正向查找指定数据的节点（从头→尾）* @param data 要查找的数据* @return 存在返回true，不存在返回false*/
public boolean search(double data) {if (head == null) {return false;}DoublyNode current = head;while (true) {if (current.data == data) {return true;}current = current.next;// 指针回到头节点 → 遍历完成未找到if (current == head) {break;}}return false;
}

反向查找指定数据的节点（从尾→头）

/*** 反向查找指定数据的节点（从尾→头）* @param data 要查找的数据* @return 存在返回true，不存在返回false*/
public boolean searchFromTail(double data) {if (head == null) {return false;}// 从尾节点开始查找DoublyNode current = head.prev;while (true) {if (current.data == data) {return true;}current = current.prev;// 指针回到尾节点 → 遍历完成未找到if (current == head.prev) {break;}}return false;
}

更新

算法步骤

1. 如果链表为空，返回失败
2. 遍历链表查找目标节点
3. 如果找到目标节点，更新其数据并返回True
4. 如果遍历完整个链表都没有找到，返回False

/*** 更新指定旧数据的节点为新数据* @param oldData 旧数据* @param newData 新数据* @return 更新成功返回true，失败返回false*/
public boolean update(double oldData, double newData) {if (head == null) {return false;}DoublyNode current = head;while (true) {if (current.data == oldData) {current.data = newData;return true;}current = current.next;// 指针回到头节点 → 遍历完成未找到if (current == head) {break;}}return false;
}

完整代码

import java.util.ArrayList;
import java.util.List;
/*** @Author Stringzhua* @Date 2025/10/23 16:55* description:循环双向链表*/
public class CircularDoublyLinkedList {// 循环双向链表的节点内部类static class DoublyNode {double data;       // 支持整数/小数（适配原代码测试数据）DoublyNode next;   // 指向下一个节点的引用DoublyNode prev;   // 指向前一个节点的引用// 节点构造方法public DoublyNode(double data) {this.data = data;this.next = null;this.prev = null;}}private DoublyNode head;  // 链表头节点（唯一入口，尾节点通过head.prev获取）// 循环双向链表构造方法（初始化空链表）public CircularDoublyLinkedList() {this.head = null;}/*** 检查链表是否为空* @return 空返回true，非空返回false*/public boolean isEmpty() {return head == null;}/*** 正向遍历链表（从头→尾）* @return 存储节点数据的List集合*/public List<Double> traverse() {List<Double> result = new ArrayList<>();if (head == null) {return result;}// 采用do-while逻辑：先添加头节点，再循环遍历后续节点DoublyNode current = head;result.add(current.data);current = current.next;// 指针回到头节点时停止（循环链表闭环特性）while (current != head) {result.add(current.data);current = current.next;}return result;}/*** 反向遍历链表（从尾→头）* @return 存储节点数据的List集合*/public List<Double> reverseTraverse() {List<Double> result = new ArrayList<>();if (head == null) {return result;}// 尾节点 = 头节点的prev，从尾节点开始遍历DoublyNode current = head.prev;result.add(current.data);current = current.prev;// 指针回到尾节点时停止while (current != head.prev) {result.add(current.data);current = current.prev;}return result;}/*** 空链表专用：插入第一个节点（形成自闭环）* @param data 节点数据* @return 插入成功返回true*/private boolean insertEmpty(double data) {DoublyNode newNode = new DoublyNode(data);head = newNode;// 自闭环：节点的next和prev都指向自身newNode.next = newNode;newNode.prev = newNode;return true;}/*** 尾插法：在链表尾部插入节点* @param data 节点数据* @return 插入成功返回true*/public boolean append(double data) {// 空链表直接调用专用插入方法if (head == null) {return insertEmpty(data);}DoublyNode newNode = new DoublyNode(data);DoublyNode tail = head.prev;  // 快速获取尾节点（无需遍历）// 1. 新节点建立双向连接：prev连尾节点，next连头节点（维持闭环）newNode.prev = tail;newNode.next = head;// 2. 更新原尾节点和头节点的连接tail.next = newNode;head.prev = newNode;return true;}/*** 头插法：在链表头部插入节点* @param data 节点数据* @return 插入成功返回true*/public boolean prepend(double data) {// 复用append逻辑：先插入到尾部，再将头节点指向新节点（原尾部）append(data);head = head.prev;  // 新节点是原尾部，head.prev指向它return true;}/*** 在指定数据的节点后插入新节点* @param targetData 目标节点的数据* @param data 新节点的数据* @return 插入成功返回true，失败返回false*/public boolean insertAfter(double targetData, double data) {if (head == null) {return false;}DoublyNode current = head;// 循环查找目标节点（遍历闭环）while (true) {if (current.data == targetData) {// 找到目标节点，执行双向插入DoublyNode newNode = new DoublyNode(data);// 1. 新节点连接：prev连目标节点，next连目标节点的原后继newNode.prev = current;newNode.next = current.next;// 2. 原后继节点的prev指向新节点current.next.prev = newNode;// 3. 目标节点的next指向新节点current.next = newNode;return true;}current = current.next;// 指针回到头节点 → 遍历完成未找到目标if (current == head) {break;}}return false;}/*** 在指定数据的节点前插入新节点* @param targetData 目标节点的数据* @param data 新节点的数据* @return 插入成功返回true，失败返回false*/public boolean insertBefore(double targetData, double data) {if (head == null) {return false;}// 目标是头节点 → 直接复用prepend（头插法）if (head.data == targetData) {return prepend(data);}// 从第二个节点开始查找（避免重复检查头节点）DoublyNode current = head.next;// 遍历到回到头节点为止while (current != head) {if (current.data == targetData) {// 找到目标节点，执行双向插入DoublyNode newNode = new DoublyNode(data);// 1. 新节点连接：prev连目标节点的原前驱，next连目标节点newNode.prev = current.prev;newNode.next = current;// 2. 原前驱节点的next指向新节点current.prev.next = newNode;// 3. 目标节点的prev指向新节点current.prev = newNode;return true;}current = current.next;}return false;  // 未找到目标节点}/*** 单节点链表专用：删除唯一节点（清空链表）* @return 删除成功返回true*/private boolean deleteOnlyNode() {head = null;  // 置空head，链表变为空return true;}/*** 删除头节点* @return 删除成功返回true，失败返回false*/public boolean deleteHead() {if (head == null) {return false;}// 单节点链表 → 调用专用删除方法if (head.next == head) {return deleteOnlyNode();}DoublyNode oldHead = head;DoublyNode tail = oldHead.prev;    // 尾节点DoublyNode newHead = oldHead.next; // 新头节点（原头节点的后继）// 1. 尾节点与新头节点建立双向连接（跳过原头节点）tail.next = newHead;newHead.prev = tail;// 2. 更新头节点为新头节点head = newHead;return true;}/*** 删除尾节点* @return 删除成功返回true，失败返回false*/public boolean deleteTail() {if (head == null) {return false;}// 单节点链表 → 调用专用删除方法if (head.next == head) {return deleteOnlyNode();}DoublyNode oldTail = head.prev;    // 原尾节点DoublyNode newTail = oldTail.prev; // 新尾节点（原尾节点的前驱）// 1. 新尾节点与头节点建立双向连接（跳过原尾节点）newTail.next = head;head.prev = newTail;return true;}/*** 删除指定数据的节点（支持头/尾/中间节点）* @param data 要删除的节点数据* @return 删除成功返回true，失败返回false*/public boolean delete(double data) {if (head == null) {return false;}// 1. 单节点链表且匹配数据 → 删除唯一节点if (head.next == head && head.data == data) {return deleteOnlyNode();}// 2. 目标是头节点 → 复用deleteHeadif (head.data == data) {return deleteHead();}// 3. 目标是尾节点 → 复用deleteTailif (head.prev.data == data) {return deleteTail();}// 4. 查找中间节点（从第二个节点到倒数第二个节点）DoublyNode current = head.next;while (current != head.prev) {if (current.data == data) {// 双向跳过当前节点：前驱连后继，后继连前驱current.prev.next = current.next;current.next.prev = current.prev;return true;}current = current.next;}return false;  // 未找到目标节点}/*** 正向查找指定数据的节点（从头→尾）* @param data 要查找的数据* @return 存在返回true，不存在返回false*/public boolean search(double data) {if (head == null) {return false;}DoublyNode current = head;while (true) {if (current.data == data) {return true;}current = current.next;// 指针回到头节点 → 遍历完成未找到if (current == head) {break;}}return false;}/*** 反向查找指定数据的节点（从尾→头）* @param data 要查找的数据* @return 存在返回true，不存在返回false*/public boolean searchFromTail(double data) {if (head == null) {return false;}// 从尾节点开始查找DoublyNode current = head.prev;while (true) {if (current.data == data) {return true;}current = current.prev;// 指针回到尾节点 → 遍历完成未找到if (current == head.prev) {break;}}return false;}/*** 更新指定旧数据的节点为新数据* @param oldData 旧数据* @param newData 新数据* @return 更新成功返回true，失败返回false*/public boolean update(double oldData, double newData) {if (head == null) {return false;}DoublyNode current = head;while (true) {if (current.data == oldData) {current.data = newData;return true;}current = current.next;// 指针回到头节点 → 遍历完成未找到if (current == head) {break;}}return false;}/*** 获取链表长度（节点总数）* @return 链表长度（空链表返回0）*/public int getLength() {if (head == null) {return 0;}int count = 1;  // 初始计数：头节点DoublyNode current = head.next;// 遍历到回到头节点为止while (current != head) {count++;current = current.next;}return count;}/*** 重写toString：自定义链表字符串格式（与Python原代码输出一致）* @return 链表的字符串表示*/@Overridepublic String toString() {if (head == null) {return "空循环双向链表";}List<Double> elements = traverse();StringBuilder sb = new StringBuilder();for (double elem : elements) {// 优化显示：整数（如1.0）显示为1，小数（如2.5）保持原格式if (elem == Math.floor(elem)) {sb.append((long) elem);} else {sb.append(elem);}sb.append(" <-> ");}sb.append("...");  // 表示闭环return "循环双向链表: " + sb.toString();}// 主方法：测试循环双向链表的所有功能（与Python原代码测试逻辑完全一致）public static void main(String[] args) {CircularDoublyLinkedList dlist = new CircularDoublyLinkedList();// 1. 测试空链表System.out.println("链表为空: " + dlist.isEmpty());    // 输出：trueSystem.out.println("链表长度: " + dlist.getLength());  // 输出：0System.out.println(dlist);                            // 输出：空循环双向链表// 2. 尾插法添加元素（1→2→3→4→5）System.out.println("\n添加元素: 1, 2, 3, 4, 5");dlist.append(1);dlist.append(2);dlist.append(3);dlist.append(4);dlist.append(5);System.out.println(dlist);                            // 输出：循环双向链表: 1 <-> 2 <-> 3 <-> 4 <-> 5 <-> ...System.out.println("链表长度: " + dlist.getLength());  // 输出：5// 3. 头插法添加元素（0→1→2→3→4→5）System.out.println("\n在头部添加元素: 0");dlist.prepend(0);System.out.println(dlist);                            // 输出：循环双向链表: 0 <-> 1 <-> 2 <-> 3 <-> 4 <-> 5 <-> ...// 4. 在指定节点后插入（3后插入3.5）System.out.println("\n在3后插入: 3.5");dlist.insertAfter(3, 3.5);System.out.println(dlist);                            // 输出：循环双向链表: 0 <-> 1 <-> 2 <-> 3 <-> 3.5 <-> 4 <-> 5 <-> ...// 5. 在指定节点前插入（3前插入2.5）System.out.println("\n在3前插入: 2.5");dlist.insertBefore(3, 2.5);System.out.println(dlist);                            // 输出：循环双向链表: 0 <-> 1 <-> 2 <-> 2.5 <-> 3 <-> 3.5 <-> 4 <-> 5 <-> ...// 6. 正向/反向遍历System.out.println("\n正向遍历:");System.out.println(dlist.traverse());                 // 输出：[0.0, 1.0, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0]System.out.println("反向遍历:");System.out.println(dlist.reverseTraverse());          // 输出：[5.0, 4.0, 3.5, 3.0, 2.5, 2.0, 1.0, 0.0]// 7. 查找元素System.out.println("\n查找元素:");System.out.println("查找3: " + dlist.search(3));      // 输出：trueSystem.out.println("查找10: " + dlist.search(10));    // 输出：falseSystem.out.println("从尾部查找3: " + dlist.searchFromTail(3));  // 输出：true// 8. 更新元素（3.5→3.75）System.out.println("\n更新元素 3.5 -> 3.75");dlist.update(3.5, 3.75);System.out.println(dlist);                            // 输出：循环双向链表: 0 <-> 1 <-> 2 <-> 2.5 <-> 3 <-> 3.75 <-> 4 <-> 5 <-> ...// 9. 删除操作System.out.println("\n删除头节点");dlist.deleteHead();System.out.println(dlist);                            // 输出：循环双向链表: 1 <-> 2 <-> 2.5 <-> 3 <-> 3.75 <-> 4 <-> 5 <-> ...System.out.println("\n删除尾节点");dlist.deleteTail();System.out.println(dlist);                            // 输出：循环双向链表: 1 <-> 2 <-> 2.5 <-> 3 <-> 3.75 <-> 4 <-> ...System.out.println("\n删除节点: 3");dlist.delete(3);System.out.println(dlist);                            // 输出：循环双向链表: 1 <-> 2 <-> 2.5 <-> 3.75 <-> 4 <-> ...// 10. 清空链表System.out.println("\n删除所有节点");while (!dlist.isEmpty()) {dlist.deleteHead();}System.out.println(dlist);                            // 输出：空循环双向链表}
}

时间空间复杂度

操作	时间复杂度	说明
在头部/尾部插入	O(1)	无需遍历即可完成操作
在中间位置插入	O(n)	需要先查找插入位置
删除头部/尾部节点	O(1)	无需遍历即可完成操作
删除中间节点	O(n)	需要先查找目标节点
查找节点	O(n)	最坏情况下需要遍历整个链表
访问任意节点	O(n)	链表不支持随机访问
遍历（正向/反向）	O(n)	需要访问所有节点

循环双向链表的空间复杂度为O(n)，其中n是节点数量。每个节点需要额外存储两个指针（prev和next）。