「用Python来学微积分」14. 连续函数的运算与初等函数的连续性

一、连续函数的四则运算

定理2 如果函数 f(x) 和 g(x) 均在 x₀ 处连续，那么它们的和、差、积、商函数 f(x)±g(x)，f(x)g(x)，f(x)/g(x)（g(x₀)≠0）均在 x₀ 处连续。

下面通过Python可视化来直观理解这个定理：

import matplotlib.pyplot as plt
import numpy as npdef demonstrate_continuous_operations():x = np.linspace(-2, 2, 1000)# 定义两个连续函数f = lambda x: np.sin(x)  # 连续函数g = lambda x: x**2 + 1   # 连续函数# 计算各种运算结果f_plus_g = f(x) + g(x)   # 和函数f_minus_g = f(x) - g(x)  # 差函数f_times_g = f(x) * g(x)  # 积函数f_div_g = f(x) / g(x)    # 商函数（g(x) ≠ 0）fig, axes = plt.subplots(2, 3, figsize=(15, 10))# 原始函数axes[0,0].plot(x, f(x), 'b-', linewidth=2, label='f(x) = sin(x)')axes[0,0].set_title('连续函数 f(x)')axes[0,0].grid(True)axes[0,0].legend()axes[0,1].plot(x, g(x), 'r-', linewidth=2, label='g(x) = x² + 1')axes[0,1].set_title('连续函数 g(x)')axes[0,1].grid(True)axes[0,1].legend()# 四则运算结果axes[0,2].plot(x, f_plus_g, 'g-', linewidth=2, label='f(x) + g(x)')axes[0,2].set_title('和函数: f(x) + g(x)')axes[0,2].grid(True)axes[0,2].legend()axes[1,0].plot(x, f_minus_g, 'purple', linewidth=2, label='f(x) - g(x)')axes[1,0].set_title('差函数: f(x) - g(x)')axes[1,0].grid(True)axes[1,0].legend()axes[1,1].plot(x, f_times_g, 'orange', linewidth=2, label='f(x) × g(x)')axes[1,1].set_title('积函数: f(x) × g(x)')axes[1,1].grid(True)axes[1,1].legend()# 商函数（注意去除g(x)=0的点）mask = g(x) != 0axes[1,2].plot(x[mask], f_div_g[mask], 'brown', linewidth=2, label='f(x) / g(x)')axes[1,2].set_title('商函数: f(x) / g(x)')axes[1,2].grid(True)axes[1,2].legend()plt.tight_layout()plt.show()# 验证在x=0处的连续性x0 = 0print(f"在 x = {x0} 处:")print(f"f({x0}) = {f(x0):.6f}, g({x0}) = {g(x0):.6f}")print(f"f+g({x0}) = {f(x0) + g(x0):.6f}")print(f"f-g({x0}) = {f(x0) - g(x0):.6f}")print(f"f×g({x0}) = {f(x0) * g(x0):.6f}")print(f"f/g({x0}) = {f(x0) / g(x0):.6f}")demonstrate_continuous_operations()

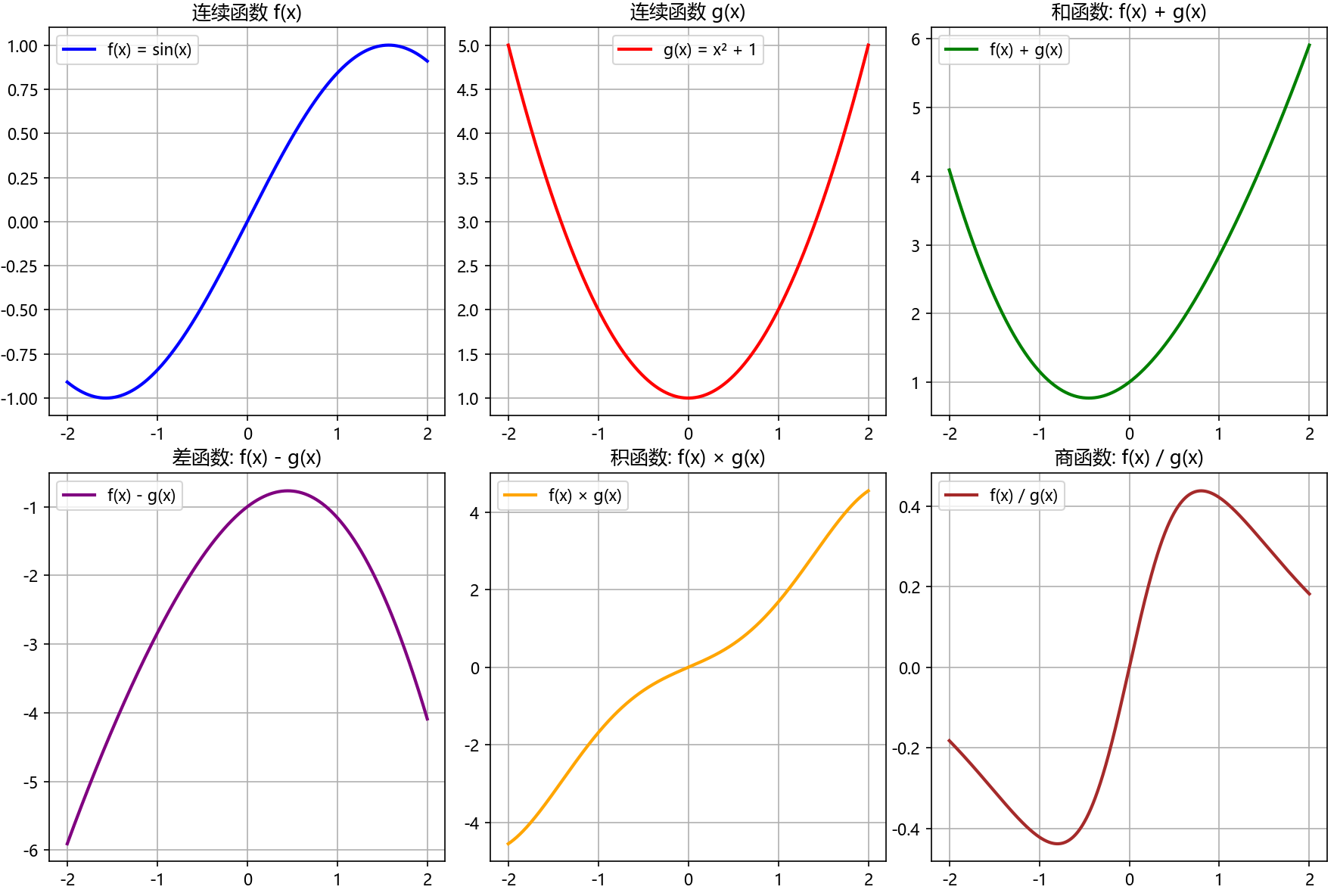
运行结果分析： 从图像可以看出，两个连续函数的和、差、积、商（分母不为零时）仍然是连续函数，验证了定理2的正确性。

二、复合函数的连续性

定理3 如果函数 f(u) 在 u₀ 处连续，函数 g(x) 在 x₀ 处连续，且 u₀ = g(x₀)，那么复合函数 f(g(x)) 在 x₀ 处连续。

从运算的角度看，在定理3的条件下，有： $$\underset{x\to x_0}{\lim }f(g(x))=f(\underset{x\to x_0}{\lim }g(x))=f(g(\underset{x\to x_0}{\lim }x))$$ 成立，即对连续函数来说，极限求值运算与函数求值运算可以交换次序。

import matplotlib.pyplot as plt
import numpy as np# 设置支持 Unicode 的字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei','DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = Falsedef demonstrate_composite_continuity():x = np.linspace(-2, 2, 1000)# 内层函数g = lambda x: x**2 + 1# 外层函数f = lambda u: np.sin(u)# 复合函数fog = lambda x: f(g(x))# 验证在x=1处的连续性x0 = 1u0 = g(x0)print("复合函数连续性验证:")print(f"x₀ = {x0}, g(x₀) = {u0:.6f}, f(g(x₀)) = {fog(x0):.6f}")print(f"lim(x→{x0}) g(x) = {g(x0):.6f}")print(f"lim(u→{u0}) f(u) = {f(u0):.6f}")print(f"lim(x→{x0}) f(g(x)) = {fog(x0):.6f}")print("由于 f(g(x₀)) = lim(x→x₀) f(g(x))，复合函数在 x₀ 处连续")# 绘制图像plt.figure(figsize=(12, 4))plt.subplot(1, 3, 1)plt.plot(x, g(x), 'b-', linewidth=2)plt.axvline(x=x0, color='r', linestyle='--', alpha=0.7)plt.axhline(y=u0, color='r', linestyle='--', alpha=0.7)plt.scatter([x0], [u0], color='red', s=50)plt.title('内层函数: g(x) = x² + 1')plt.grid(True)plt.subplot(1, 3, 2)u_values = np.linspace(0.5, 3, 1000)plt.plot(u_values, f(u_values), 'g-', linewidth=2)plt.axvline(x=u0, color='r', linestyle='--', alpha=0.7)plt.axhline(y=f(u0), color='r', linestyle='--', alpha=0.7)plt.scatter([u0], [f(u0)], color='red', s=50)plt.title('外层函数: f(u) = sin(u)')plt.grid(True)plt.subplot(1, 3, 3)plt.plot(x, fog(x), 'purple', linewidth=2)plt.axvline(x=x0, color='r', linestyle='--', alpha=0.7)plt.axhline(y=fog(x0), color='r', linestyle='--', alpha=0.7)plt.scatter([x0], [fog(x0)], color='red', s=50)plt.title('复合函数: f(g(x)) = sin(x² + 1)')plt.grid(True)plt.tight_layout()plt.show()demonstrate_composite_continuity()

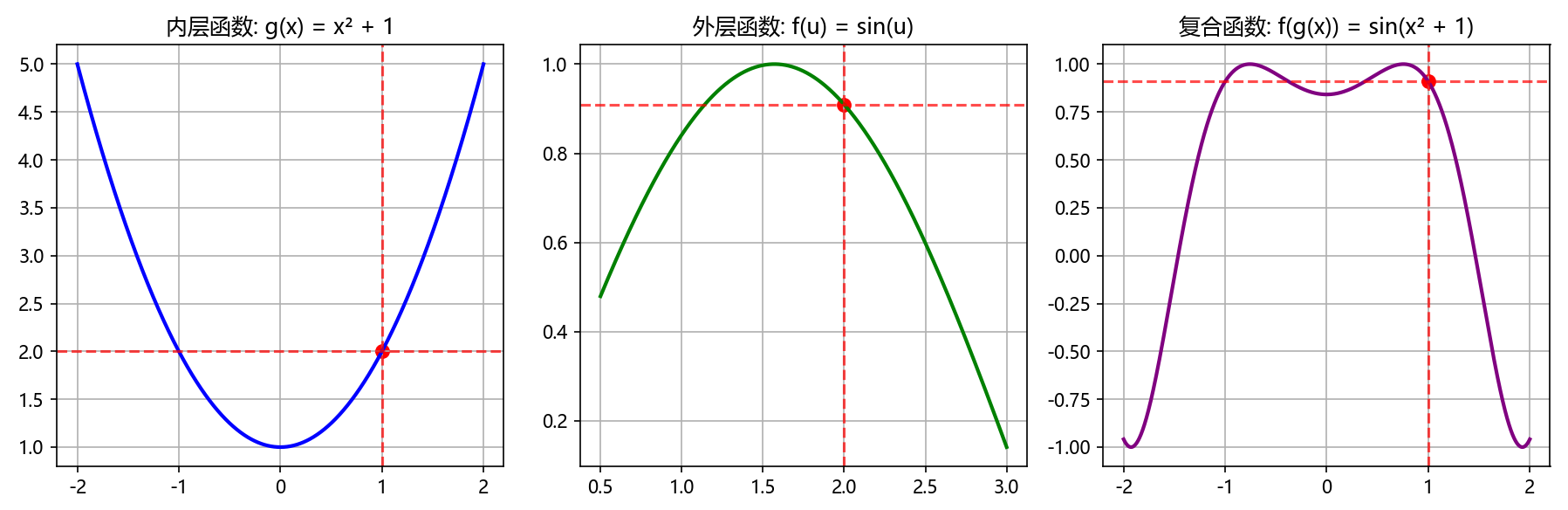
三、初等函数的连续性证明

例1：幂函数的连续性证明

证明：幂函数 $y=x^{\alpha }$ 在 $(0,+\infty )$ 内连续。

证明过程：当 $x\in (0,+\infty )$ 时，根据指数函数与对数函数的性质，得： $$y=x^{\alpha }=e^{\ln x^{\alpha }}=e^{\alpha \ln x}$$

由于对数函数与指数函数都是连续的，因此对任意的 $x_0\in (0,+\infty )$，因为函数 $\alpha \ln x$ 在 $x_0$ 处连续，且指数函数 $e^x$ 在 $u_0=\alpha \ln x_0$ 处连续，所以根据复合函数的连续性可知，幂函数 $y=x^{\alpha }=e^{\alpha \ln x}$ 在 $x_0$ 处连续。

由 $x_0$ 的任意性可知：幂函数 $y=x^{\alpha }$ 在 $(0,+\infty )$ 内连续。

def demonstrate_power_function_continuity():x = np.linspace(0.1, 3, 1000)alpha_values = [0.5, 1, 1.5, 2]  # 不同的指数plt.figure(figsize=(12, 8))for i, alpha in enumerate(alpha_values):y = x**alphaplt.subplot(2, 2, i+1)plt.plot(x, y, 'b-', linewidth=2, label=f'$y = x^{{{alpha}}}$')# 标记几个点验证连续性test_points = [0.5, 1.0, 2.0]for x0 in test_points:y0 = x0**alphaplt.scatter([x0], [y0], color='red', s=50)plt.annotate(f'({x0}, {y0:.2f})', (x0, y0), xytext=(10, 10), textcoords='offset points')plt.title(f'幂函数 $y = x^{{{alpha}}}$ 的连续性')plt.xlabel('x')plt.ylabel('y')plt.grid(True, alpha=0.3)plt.legend()plt.tight_layout()plt.show()# 验证极限运算x0 = 2for alpha in alpha_values:limit_left = (x0 - 0.001)**alphalimit_right = (x0 + 0.001)**alphaactual_value = x0**alphaprint(f"幂函数 y = x^{alpha}:")print(f"  lim(x→{x0}-) y = {limit_left:.6f}")print(f"  lim(x→{x0}+) y = {limit_right:.6f}")print(f"  y({x0}) = {actual_value:.6f}")print(f"  连续性验证: {abs(limit_left - actual_value) < 1e-5 and abs(limit_right - actual_value) < 1e-5}")print()demonstrate_power_function_continuity()

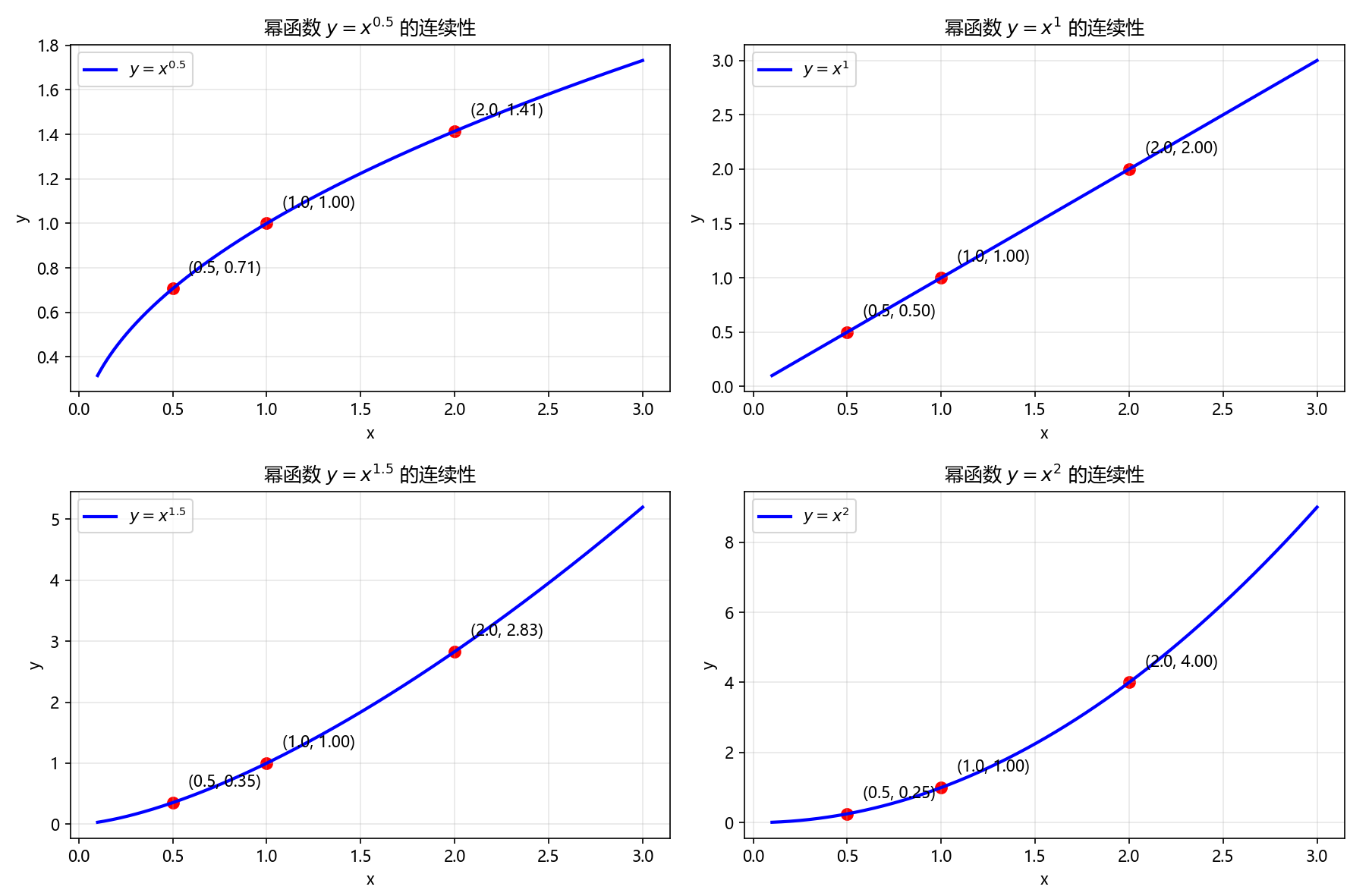
例2：指数型复合函数的连续性

证明：如果函数 f(x) 和 g(x) 均在 x₀ 处连续，且 f(x₀) > 0，则函数 $y=f(x{)}^{g(x)}$ 在 x₀ 处连续。

证明过程：根据指数函数与对数函数的性质，得： $$y=f(x{)}^{g(x)}=e^{\ln f(x{)}^{g(x)}}=e^{g(x)\ln f(x)}$$

因为函数 f(x) 在 x₀ 处连续，对数函数 $\ln u$ 在 f(x₀) 处连续，所以函数 $\ln f(x)$ 在 x₀ 处连续。

因为函数 g(x) 在 x₀ 处连续，所以函数 $g(x)\ln f(x)$ 在 x₀ 处连续。

又因为指数函数 $e^x$ 在 $v_0=g(x_0)\ln f(x_0)$ 处连续，所以 $y=e^{g(x)\ln f(x)}$ 在 x₀ 处连续。

import matplotlib.pyplot as plt
import numpy as np# 设置支持 Unicode 的字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = Falsedef demonstrate_exponential_composite_continuity():x = np.linspace(0.5, 2.5, 1000)# 定义f(x)和g(x)，在x=1处都连续f = lambda x: x**2 + 1  # f(1) = 2 > 0g = lambda x: 2*x + 1# 指数型复合函数y = f(x)**g(x)# 验证在x=1处的连续性x0 = 1f_x0 = f(x0)g_x0 = g(x0)y_x0 = f_x0**g_x0print("指数型复合函数连续性验证:")print(f"在 x = {x0} 处:")print(f"f({x0}) = {f_x0} > 0")print(f"g({x0}) = {g_x0}")# 修复这里：使用g(x0)而不是g({x0})print(f"y({x0}) = f({x0})^{g(x0)} = {y_x0:.6f}")# 计算左右极限x_left = x0 - 0.001x_right = x0 + 0.001y_left = f(x_left)**g(x_left)y_right = f(x_right)**g(x_right)print(f"lim(x→{x0}-) y = {y_left:.6f}")print(f"lim(x→{x0}+) y = {y_right:.6f}")print(f"连续性成立: {abs(y_left - y_x0) < 1e-4 and abs(y_right - y_x0) < 1e-4}")# 绘制图像plt.figure(figsize=(10, 8))plt.subplot(2, 2, 1)plt.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x² + 1')plt.axvline(x=x0, color='r', linestyle='--', alpha=0.7)plt.scatter([x0], [f_x0], color='red', s=50)plt.title('函数 f(x)')plt.grid(True)plt.legend()plt.subplot(2, 2, 2)plt.plot(x, g(x), 'g-', linewidth=2, label='g(x) = 2x + 1')plt.axvline(x=x0, color='r', linestyle='--', alpha=0.7)plt.scatter([x0], [g_x0], color='red', s=50)plt.title('函数 g(x)')plt.grid(True)plt.legend()plt.subplot(2, 2, 3)# 使用对数变换避免数值问题log_y = g(x) * np.log(f(x))plt.plot(x, log_y, 'orange', linewidth=2, label='g(x)lnf(x)')plt.axvline(x=x0, color='r', linestyle='--', alpha=0.7)plt.scatter([x0], [g_x0 * np.log(f_x0)], color='red', s=50)plt.title('中间函数: g(x)lnf(x)')plt.grid(True)plt.legend()plt.subplot(2, 2, 4)plt.plot(x, y, 'purple', linewidth=2, label='y = f(x)^g(x)')plt.axvline(x=x0, color='r', linestyle='--', alpha=0.7)plt.scatter([x0], [y_x0], color='red', s=50)plt.title('指数型复合函数')plt.grid(True)plt.legend()plt.tight_layout()plt.show()# 调用函数
demonstrate_exponential_composite_continuity()

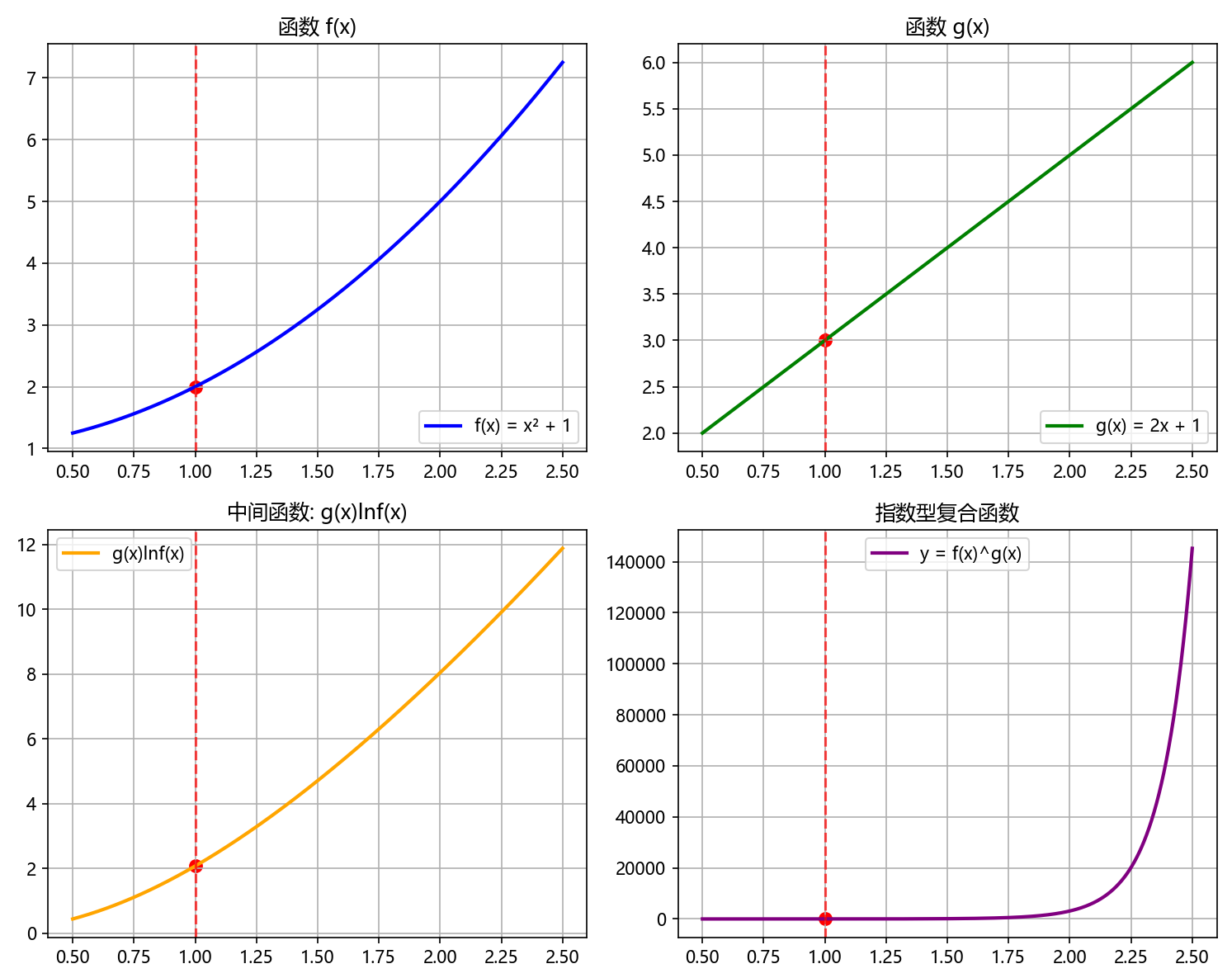
四、初等函数连续性总结

基于前面的证明，我们可以总结出以下重要结论：

1. 基本初等函数（幂函数、指数函数、对数函数、三角函数、反三角函数）在其定义域内都是连续的
2. 连续函数的四则运算结果仍然是连续函数（除法要求分母不为零）
3. 复合函数在满足条件时也是连续的
4. 所有初等函数在其定义区间内都是连续的

五、应用实例：连续函数在极限计算中的应用

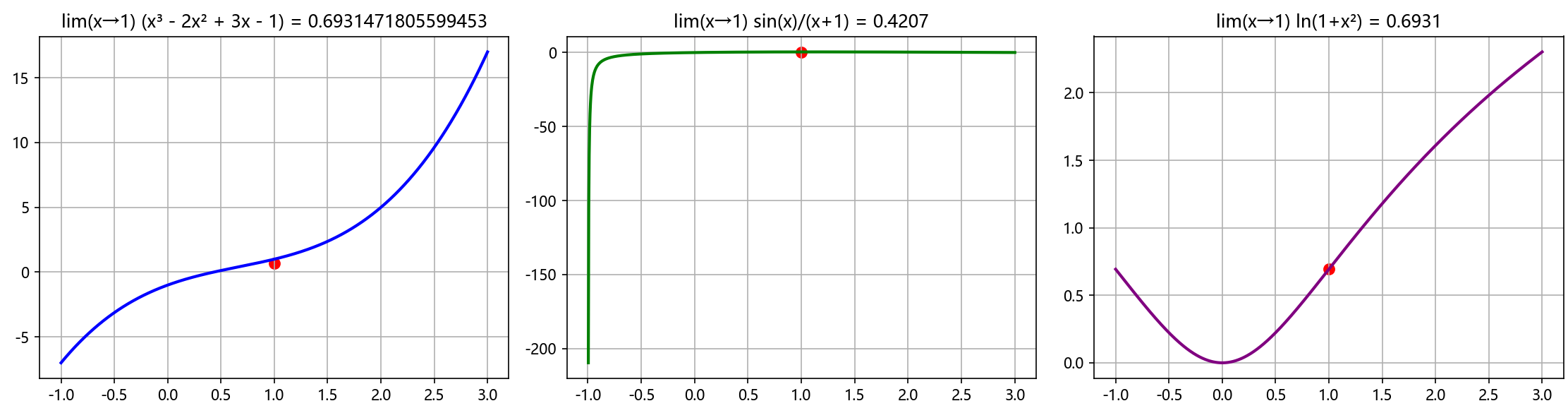
连续函数的性质在极限计算中有着重要应用。由于初等函数在其定义域内连续，我们可以直接代入计算极限值。

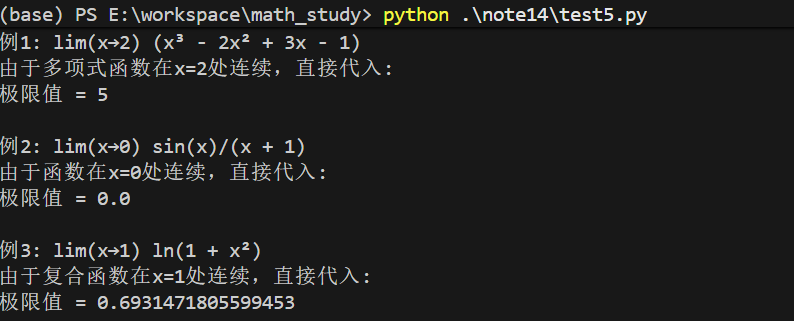
def demonstrate_continuity_in_limit_calculation():print("连续函数在极限计算中的应用示例:")print("=" * 50)# 示例1：多项式函数的极限def poly_func(x):return x**3 - 2*x**2 + 3*x - 1x0 = 2limit_value = poly_func(x0)print(f"例1: lim(x→{x0}) (x³ - 2x² + 3x - 1)")print(f"由于多项式函数在x={x0}处连续，直接代入:")print(f"极限值 = {limit_value}")print()# 示例2：三角函数的极限def trig_func(x):return np.sin(x) / (x + 1)  # 在x=0处连续x0 = 0limit_value = trig_func(x0)print(f"例2: lim(x→{x0}) sin(x)/(x + 1)")print(f"由于函数在x={x0}处连续，直接代入:")print(f"极限值 = {limit_value}")print()# 示例3：复合函数的极限def composite_func(x):return np.log(1 + x**2)  # 在x=1处连续x0 = 1limit_value = composite_func(x0)print(f"例3: lim(x→{x0}) ln(1 + x²)")print(f"由于复合函数在x={x0}处连续，直接代入:")print(f"极限值 = {limit_value}")print()# 可视化验证x = np.linspace(-1, 3, 1000)plt.figure(figsize=(15, 4))plt.subplot(1, 3, 1)y1 = poly_func(x)plt.plot(x, y1, 'b-', linewidth=2)plt.scatter([x0], [limit_value], color='red', s=50)plt.title(f'lim(x→{x0}) (x³ - 2x² + 3x - 1) = {limit_value}')plt.grid(True)plt.subplot(1, 3, 2)y2 = trig_func(x)plt.plot(x, y2, 'g-', linewidth=2)plt.scatter([x0], [trig_func(x0)], color='red', s=50)plt.title(f'lim(x→{x0}) sin(x)/(x+1) = {trig_func(x0):.4f}')plt.grid(True)plt.subplot(1, 3, 3)y3 = composite_func(x)plt.plot(x, y3, 'purple', linewidth=2)plt.scatter([x0], [composite_func(x0)], color='red', s=50)plt.title(f'lim(x→{x0}) ln(1+x²) = {composite_func(x0):.4f}')plt.grid(True)plt.tight_layout()plt.show()demonstrate_continuity_in_limit_calculation()

总结

通过本文的分析和Python可视化，我们可以清晰地看到：

1. 连续函数的运算性质：连续函数经过四则运算和复合运算后，在满足条件的情况下仍然保持连续性
2. 初等函数的连续性：所有初等函数在其定义域内都是连续的
3. 实际应用价值：连续性性质大大简化了极限计算，对于连续函数可以直接代入求极限

这些性质不仅是数学分析的理论基础，也在工程计算和科学研究中有着广泛的应用。通过Python可视化，我们能够更直观地理解这些抽象的数学概念，将理论与实践完美结合。

关键词：连续函数、初等函数、极限计算、Python可视化、微积分

---

参考资料：

1. 扈志明，《微积分》，高等教育出版社

欢迎点赞、收藏、评论，您的支持是我持续创作的最大动力！如有任何疑问，欢迎在评论区提出，我会尽快解答。。