当前位置：首页 > news >正文

022数据结构之树状数组——算法备赛

news 2025/10/25 7:47:32

树状数组

树状数组是用来解决动态数组（会多次修改其中的元素值）多次求区间和的效率瓶颈问题的。

在树状数组没有发明出来之前，求动态数组的区间和会怎么做呢？

对于一个数组a，维护它的前缀和数组sum，sum[i]表示a数组[0,i]的区间和，对于任意的[i,j]区间和可以用sum[j]-sum[i-1]求出。当数组a是静止（元素不发生改变）的时，求区间和的时间复杂度为O(1)；当数组a动态时，求区间和的复杂度最坏是O(n)。如：修改a[i],连带得sum[i],sum[i+1],...,sum[n-1]都需要修改。

树状数组就是解决这个需要大量连带修改的效率低的问题的。它具体是怎么做的，且听我娓娓道来…

树状数组解决的痛点问题

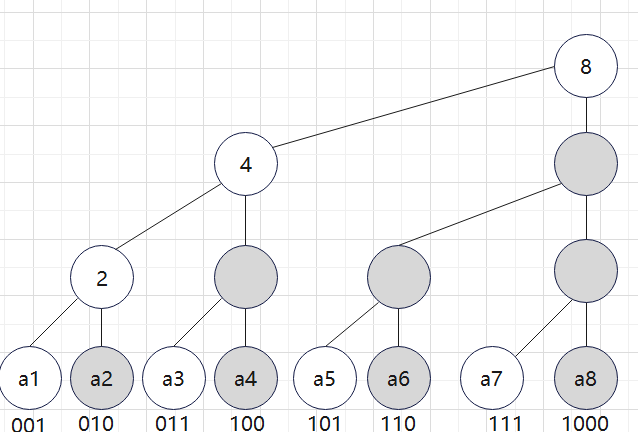
树状数组是利用数的二进制特征进行检索的一种树状结构，可实现高效率查询和维护前缀和。

树状数组的内部维护的是一个数组tree，他是根据对原数组a特殊计算而来(下文中的tree和a都是这个含义)。令i的二进制的最后一个1是t tree[i]储存的是a( i-t , i ]的区间和（注意不包含a[i-t]）。特殊地，tree[0] = 0。

如：tree[0x1100] = a[0x1000]+a[0x1001]+...+a[0x1100]即：tree[12] = tree[8]+tree[9]+...+tree[12]。

由上述定义，可推导出原数组a的前缀和sum(i)等于 i的所有【二进制为1的位向后截断】后的值对应的tree值的和，

如：sum(0x10110) = tree[0x10] + tree[0x110] + tr[0x10110]即：sum(22) = tree[2] + tree[6] + tree[22]

求前缀和的最坏时间复杂度为O(logn)。
一开始求sum(i)直接与数组a有关，现在求sum(i)只与数组有关tree，当a[i]修改，不需要连带修改sum[i],sum[i+1],...sum[n-1]了，而是修改tree，设a的数组最大下标为0x11011(27)，修改a[0x11]，只需修改tree[1011],tree[11011]，

单点修改a[i]的最坏时间复杂度为O(logn)。
有了求原数组a的前缀和的sum(i)方法，任意的区间[i,j]的和就是sum[j] - sum[i-1]。

神奇的lowbit(x)

lowbit(x)=x&(-x) ,功能就是找到x的二进制的最后一个1。

其原理是利用了负数的补码表示形式。

负数的补码为对应正数补码按位取反再加1 例6—>00000110 -6—>11111010.

令m=lowbit(x); tree[x]的值是将a[x]和它后面共m个数相加的结果。

由此可得tree[x]的标准定义：tree[x]中储存的是原数组a的[x-lowbit(x)+1,x]区间和。

横条上的黑色部分表示tree[x],它表示横条上元素相加的和。

在这里插入图片描述

查询的过程

查询过程每次减lowbit（x）

定义树状数组 tree[]

例 7的二进制为111，去掉最后一个1，得110，即tree[6];
去掉6的二进制的110的最后一个1，得100，即tree[4];
4的二进制100，去掉1后没有了，结束。

维护过程

维护过程每次加lowbit（x）

维护的过程是在二进制最后的1加上1.例如更新了a3，需要修改tree[3],tree[4],tree[8]等。

3的二进制为11，最后的1加1得100，即修改tree[4];
4的二进制为100，最后的1加1得1000，即修改tree[8];
继续修改tree[16]，tree[32]等。

在这里插入图片描述

单点修改+区间查询

const int N=1000;
#define lowbit(x) ((x)&(-x))
int tree[N]={0};  //初始化都为0  用可变数组vector<int>tree(n,0);
void update(int x,int d){  //单点修改：修改元素a[x],a[x]=a[x]+dwhile(x<=N){  //N对应tree.size()tree[x]+=d;x+=lowbit(x);}//for(int i=x;x<=N;i+=lowbit(i)) tree[x]+=d;  //向上维护
}
int sum(int x){  //查询前缀和int ans=0;//for(int i=x;x>0;i-=lowbit(i)) ans+=tree[x]; //向下查找while(x>0){ans+=tree[x];x-=lowbit(x);}    return ans;
}
//以上是树状数组
int a[11]={0,4,5,6,7,8,9,10,11,12,13}  //注意，a[0]不用
void Init(){  //初始化for(int i=1;i<=10;i++){update(i,a[i]);}
}
//查询任意区间[i,j]的前缀和为  sum(j)-sum(i-1);

模版封装

封装成类Class（更通用）

class Fenwick {
private:vector<int> tree;  public:Fenwick(int n) : tree(n+2, 0) {}  //0下标不用,最后多一个下标防止change方法越界报错void add(int i) {  //单点a[i]加1，虚拟sum[i,n-1]全部加1while (i < tree.size()) {tree[i]++;i += i & -i;}}void add(int i,int d){  //单点a[i]+d,虚拟sum[i,n-1]全部加d，方法重载while (i < tree.size()) {tree[i]+=d;i += i & -i;}}void change(int l,int r){  //单点a[l]+1,a[r+1]-1,tree区间修改add(l);add(r+1,-1);}void change(int l,int r,int d){  //单点a[l]+d,a[r+1]-d,tree区间修改,方法重载add(l,d);add(r+1,-d);}// [1,i] 中的元素和，前缀和int sum(int i) {int res = 0;while (i > 0) {res += tree[i];i -= i & -i;}return res;}// [l,r] 中的元素和，区间和int query(int l, int r) {return sum(r) - sum(l - 1);}
};

add(i,d)为单点修改操作，相当于对原数组a做修改操作：a[i]+=d
change(l,r,d)为两次单点修改，相当于对原数组a做两次修改操作：a[l]+=d,a[r+1]-=d，若a是sum数组的差分数组，相当于对sum区间[l,r]内所有元素都加d。这里需要注意并不是对原数组 a 做区间修改操作。

封装成数据结构struct（更适合比赛时手搓）

struct F {int n;vector<int> v;F(int n) : n(n), v(n + 1) {};  //原数组下标从0开始void add(int i, int d=1) {for (++i; i <= n; i += i & -i)v[i] += d;}int sum(int i) const {int s = 0;for (++i; i; i -= i & -i)s += v[i];return s;}int query(int l, int r) const { return l > r ? 0 : sum(r) - (l ? sum(l - 1) : 0); }
};

应用

偏序问题

一维偏序问题

问题描述

给定数列a，求i<j且ai>aj的二元组的数量。

逆序对问题有两种标准解法，即归并排序和树状数组。他们的复杂度均是O(nlogn),

不过归并排序有一个固有的缺点，就是它需要多次复制数组。

分析

把数字看作树状数组下标，{5,4,2,6,3,1}对应a[5],a[4],a[2],a[6],a[3],a[1]。初始元素值为0，每处理一个数字，树状数组的原数组下标对应的元素值加一，统计前缀和，就是逆序对的数量。
用树状数组倒序处理数列，当前数字的前一个数的前缀和即为以该数为较大数的逆序对个数。例

从数列末端开始

数字1，把a[1]加1，计算a[1]前一个数的前缀和sum(0),逆序对数量ans+=sum(0)=0;

数字3，把a[3]加1，计算a[3]前一个数的前缀和sum(2),逆序对数量ans+=sum(2)=1;

数字6，把a[6]加1，计算a[6]前一个数的前缀和sum(5),逆序对数量ans+=sum(5)=3;

…

每次更改a[i]，sum[i] , sum[i+1] , sum[i+2]…都要做更新，使用树状数组能在O（logn）时间复杂度内完成。
上面的处理方法有一个问题，如果数字过大，那么树状数组的空间就远远超过题目限制。用离散化能很好解决这个问题。

离散化就是把原来的数值用他的相对大小替代，而顺序任然不变，不影响实际计算。有多少个数值，离散化后的N就有多大。

代码

const N=500010；
int tree[N]={0},r[N],n;  //tree为树状数组，r为离散化的元素数组，n为数组大小。
struct point{int num,val;}a[N];
bool cmp(point x,point y){  //离散化需要用到排序if(x.val==y.val) return x.num<y,num;  //如果值相等，让先出现（下标小的）的排在前面return x,val<y.val;
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i].val;a[i].num=i;  //记录a数组顺序（原数组下标）}sort(a+1,a+n+1,cmp); //升序排序for(int i=1;i<=n;i++) r[a[i].num]=i;  //离散化，得到新的数字序列r，r为后续要处理的数组。long long ans=0;for(int i=n;i>0;i--){  //倒序处理update(r[i],1);  //update(),sum()代码前面已给出。ans+=sum(r[i]-1);}cout<<ans;return 0;
}

压制二元组的总价值

问题描述

给定大小为N的排列A，B 若一对二元组下标满足以下关系，则被称为压制二元组。

1<=i<j<=n;
p(Ai)<p(Aj); (P(x)为x在B数组中的下标)

一对压制二元组的价值为 j-i，请计算所有压制二元组价值之和。

代码

#include <iostream>
#include<algorithm>
#include<vector>
#define ll long long
#define lowbit(x) ((x)&(-x))
using namespace std;
class Tree{private:vector<ll>date1;vector<ll>date2;public:Tree(int n){  //初始化date1和date2.date1=vector<ll>(n+1,0);date2=vector<ll>(n+1,0);}void update(int x,int d){long long t=x;int s=date1.size();while(x<=s){date1[x]+=d;  //每次加d，即1date2[x]+=t;  //每次加x 即data2下标x+=lowbit(x);}}long long sum(int x){int t=x+1;  //t代表【i,j】中的jll ans1=0,ans2=0;  //ans1为个数前缀和（即前面有多少个A下标值小于等于x的个数），ans2为数量前缀合（即前面A下标值小于等于x的下标量之和）while(x>0){ans1+=date1[x];ans2+=date2[x];x-=lowbit(x);}return t*ans1-ans2; //返回[1,x]中以x为较大值 的压制二元组价值之和}
};
struct pr{int num,val;};
int main()
{// 请在此输入您的代码int n;ll ans=0;cin>>n;Tree tree(n); vector<pr>A(n+1);vector<int>C(n+1); //C[i]储存的是B中i的下标for(int i=1;i<=n;i++){cin>>A[i].val;  //储存值A[i].num=i;  //储存下标}for(int i=1;i<=n;i++){int x;cin>>x;C[x]=i;  //记录x的下标}auto cmp=[&](pr x,pr y){return C[x.val]<C[y.val];};sort(A.begin(),A.end(),cmp);  //按A[i].val在B中的下标大小排序for(int i=1;i<=n;i++){ans+=tree.sum(A[i].num-1);tree.update(A[i].num,1);  //每次计算完更新。}cout<<ans;
}

翻转对

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。

你需要返回给定数组中的重要翻转对的数量。

代码

class BIT {
private:vector<int> tree;int n;public:BIT(int _n) : n(_n), tree(_n + 1) {}static constexpr int lowbit(int x) {return x & (-x);}void update(int x, int d) {while (x <= n) {tree[x] += d;x += lowbit(x);}}int query(int x) const {int ans = 0;while (x) {ans += tree[x];x -= lowbit(x);}return ans;}
};class Solution {
public:int reversePairs(vector<int>& nums) {set<long long> allNumbers;  //有序哈希容器，不允许重复for (int x : nums) {allNumbers.insert(x);allNumbers.insert((long long)x * 2);}//利用哈希表进行离散化unordered_map<long long, int> values;int idx = 0;for(long long x:allNumbers){values[x]=++idx;}int ret = 0;BIT bit(values.size());int n=values.size();for (int i = 0; i < nums.size(); i++) {int left = values[(long long)nums[i] * 2];  //查询nums[i]*2在原数组的下标//查询值大于nums[i] * 2的数量，bit.query(n)为当前统计总数，bit.query(left)为前面统计的小于等于nums[i]*2的总数ret += bit.query(n) - bit.query(left);  bit.update(values[nums[i]], 1);  //每次查询完做更新前缀和}return ret;}
};

其他问题

用点构造面积最大的矩形||

问题描述

在无限平面上有 n 个点。给定两个整数数组 xCoord 和 yCoord，其中 (xCoord[i], yCoord[i]) 表示第 i 个点的坐标。

你的任务是找出满足以下条件的矩形可能的最大面积：

矩形的四个顶点必须是数组中的四个点。
矩形的内部或边界上不能包含任何其他点。
矩形的边与坐标轴平行。

返回可以获得的 最大面积 ，如果无法形成这样的矩形，则返回 -1。

原题链接

代码

class Fenwick {
private:vector<int> tree;  public:Fenwick(int n) : tree(n+2, 0) {}  //0下标不用,最后多一个下标防止change方法越界报错void add(int i) {  //单点a[i]加1，虚拟sum[i,n-1]全部加1while (i < tree.size()) {tree[i]++;i += i & -i;}}void add(int i,int d){  //单点a[i]+d,虚拟sum[i,n-1]全部加d，方法重载while (i < tree.size()) {tree[i]+=d;i += i & -i;}}void change(int l,int r){  //单点a[l]+1,a[r+1]-1,tree区间修改add(l);add(r+1,-1);}void change(int l,int r,int d){  //单点a[l]+d,a[r+1]-d,tree区间修改,方法重载add(l,d);add(r+1,-d);}// [1,i] 中的元素和，前缀和int sum(int i) {int res = 0;while (i > 0) {res += tree[i];i -= i & -i;}return res;}// [l,r] 中的元素和，区间和int query(int l, int r) {return sum(r) - sum(l - 1);}
};
class Solution{
public:
long long maxRectangleArea(vector<int>& xCoord, vector<int>& ys) {vector<pair<int, int>> points;for (int i = 0; i < xCoord.size(); i++) {points.emplace_back(xCoord[i], ys[i]);}ranges::sort(points);// 离散化用ranges::sort(ys);unordered_map<int,int>mp;int cnt=2; mp[ys[0]]=1;for(int i=1;i<ys.size();i++){if(ys[i]!=ys[i-1]) mp[ys[i]]=cnt++;}long long ans = -1;Fenwick tree(ys.size());tree.add(mp[points[0].second]);vector<tuple<int, int, int>> pre(mp.size(), {-1, -1, -1});for (int i = 1; i < points.size(); i++) {auto& [x1, y1] = points[i - 1];auto& [x2, y2] = points[i];int y = mp[y2]; // 离散化tree.add(y);if (x1 != x2) { // 两点不在同一列continue;}int cur = tree.query(mp[y1], y);auto& [pre_x, pre_y, p] = pre[y-1];if (pre_y == y1 && p + 2 == cur) {ans = max(ans, (long long) (x2 - pre_x) * (y2 - y1));}pre[y-1] = {x1, y1, cur};}return ans;}
};

位计数深度为k的整数数目||

问题描述

给你一个整数数组 nums。

对于任意正整数 x，定义以下序列：

p0 = x
pi+1 = popcount(pi)，对于所有 i >= 0，其中 popcount(y) 表示整数 y 的二进制表示中 1 的个数。

这个序列最终会收敛到值 1。

popcount-depth（位计数深度）定义为满足 pd = 1 的最小整数 d >= 0。

例如，当 x = 7（二进制表示为 "111"）时，该序列为：7 → 3 → 2 → 1，因此 7 的 popcount-depth 为 3。

此外，给定一个二维整数数组 queries，其中每个 queries[i] 可以是以下两种类型之一：

[1, l, r, k] - 计算在区间 [l, r] 中，满足 nums[j] 的 popcount-depth 等于 k 的索引 j 的数量。
[2, idx, val] - 将 nums[idx] 更新为 val。

返回一个整数数组 answer，其中 answer[i] 表示第 i 个类型为 [1, l, r, k] 的查询的结果。

原题链接

代码

struct F {int n;vector<int> v;F(int n) : n(n), v(n + 1) {};  //原数组下标从0开始void add(int i, int d=1) {for (++i; i <= n; i += i & -i)v[i] += d;}int sum(int i) const {int s = 0;for (++i; i; i -= i & -i)s += v[i];return s;}int query(int l, int r) const { return l > r ? 0 : sum(r) - (l ? sum(l - 1) : 0); }
};class Solution {int getDeep(long long x) {int d = 0;while (x > 1) {x = __builtin_popcountll(x);++d;}return d;}public:vector<int> popcountDepth(vector<long long>& A,vector<vector<long long>>& Q) {int n = A.size();vector<int> d(n), ans;vector<F> Fens(6,F(n));for (int i = 0; i < n; ++i) {d[i] = getDeep(A[i]);Fens[d[i]].add(i, 1);}for (auto& q : Q) {if (q[0] == 1) {ans.push_back(Fens[q[3]].query(q[1], q[2]));  //查询答案} else {int i = q[1], oldDeep = d[i], newDeep = getDeep(q[2]);if (oldDeep != newDeep) {Fens[oldDeep].add(i, -1);Fens[newDeep].add(i);d[i] = newDeep;  //更新深度值}}}return ans;}
};