当前位置：首页 > news >正文

【C++闯关笔记】map与set底层：二叉搜索树

news 2025/10/24 17:09:43

系列文章目录

上篇笔记：【C++闯关笔记】深究继承-CSDN博客

文章目录

目录

系列文章目录

文章目录

前言

一、什么是二叉搜索树

1.二叉搜索树的概念

2.为什么设计出二叉搜索树——性能分析

二、搜索二叉树如何插入、删除数据

1.插入数据

2.删除数据

3.在已有数据种查找数据

三、综上完整搜索二叉树代码

前言

为什么要了解二叉搜索树？

因为map/set/multimap/multiset系列容器底层就是二叉搜索树实现的，而 map 和 set 又是STL中使用频率非常高的容器，为此本文将详细介绍二叉搜索树的概念与性质，最后尝试模拟实现它。

一、什么是二叉搜索树

二叉搜索树是基于二叉树的基础之上衍生而出的一个子类，而二叉树就是形如下的一种数据结构——模拟现实世界中的“二叉树”，即使不了解二叉树相关内容也不妨碍阅读本文。

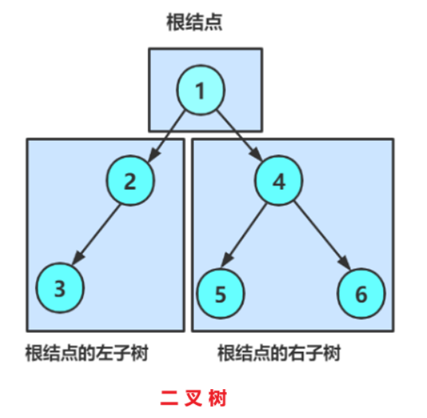
1.二叉搜索树的概念

二叉搜索树又称二叉排序树，它是具有以下性质的二叉树：

①若左子树不为空，则左子树上所有结点的值都小于等于根结点的值；

②若右子树不为空，则右子树上所有结点的值都大于等于根结点的值；

③它的左右子树也分别为二叉搜索树。

如下图所示：

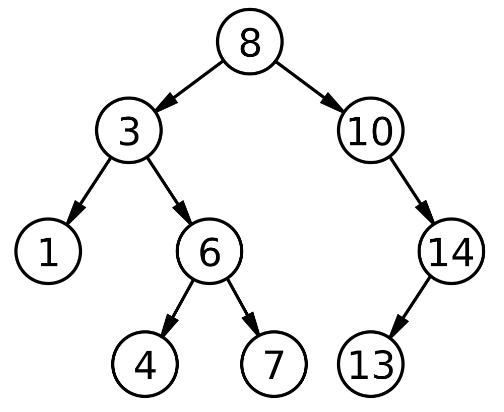
2.为什么设计出二叉搜索树——性能分析

由于二叉搜索树的性质，用于存储数据十分便捷：查找数据时，与根节点对比一次就可以排除 1/2 的数据。

在最优的情况下，即二叉搜索树为完全二叉树(或者接近完全二叉树，如上图所示)，排查数据的时间复杂度可以达到 O(log2N)；最坏的情况下，即树只有一侧有数据，时间复杂读也有O(N)。

相较于同为O(log2N)二分查找，二叉搜索树却没有以下缺陷：

1).需要存储在支持下标随机访问的结构中，并且有序。

2).插入和删除数据效率很低，因为存储在下标随机访问的结构中，插入和删除数据一般需要挪动数据。

在之后的AVL树与红黑树正是通过一些算法平衡之后的搜索二叉树，使其时间复杂度稳定在O(log2N)附近，由此也可以看出二叉搜索树的重要性与价值。

二、搜索二叉树如何插入、删除数据

搜索二叉树的节点定义与类成员变量，同链式二叉树、链表结构类似，这里就直接给出，若有疑问欢迎在评论区讨论：

namespace karsen
{template<class K>struct BSTNode{K _key;BSTNode* _left;BSTNode* _right;BSTNode(const K& key):_key(key),_left(nullptr),_right(nullptr){ }};template<class K>class BSTree{public:typedef BSTNode<K> BSTNode;private:BSTNode* _root = nullptr;};
}

1.插入数据

inta[]={8,3,1,10,6,4,7,14,13};

具体过程分三种情形：

1.树本身为空，则直接数据作为根节点；

2.树不空，按二叉搜索树性质，插入值比当前结点大往右走，插入值比当前结点小往左走，找到空位置，插入新结点。

3.如果支持插入相等的值，插入值跟当前结点相等的值可以往右走，也可以往左走，找到空位置，插入新结点。（支持插入相等节点，即multiset / multmap；不支持插入相同节点，即set / map)。

依照上述内容，那么a[ ]数组排成的搜索二叉树如下所示：

将插入的可能情形与处理，用代码给出：

	template<class K>class BSTree{public:typedef BSTNode<K> BSTNode;bool Insert(const K& k){//情况一if (_root == nullptr){_root = new BSTNode(k);return true;}//情况二，这里不允许相同值else{BSTNode* parent = _root;BSTNode* cur = parent;while (cur){if (k < cur->_key){parent = cur;cur = cur->_left;}else if (k > cur->_key){parent = cur;cur = cur->_right;}else{//不允许插入相等值return false;}}BSTNode* newNode = new BSTNode(k);if (k <= parent->_key){parent->_left = newNode;return true;}else{parent->_right = newNode;return true;}return false;}private:BSTNode* _root = nullptr;};

2.删除数据

首先分为两类：

1）元素是否在二叉搜索树中，如果不存在，则不用其他操作直接返回false。

2）如果查找元素存在，则分以下四种情况分别处理：（假设要删除的结点为N）

①要删除结点N左右孩子均为空；

②要删除的结点N左孩子空，右孩子结点不为空；

③要删除的结点N右孩子空，左孩子结点不为空；

④要删除的结点N左右孩子结点均不为空；

对应以上四种情况的解决方案：

①把N结点的父亲对应孩子的指针指向空，直接删除N结点；

②把N结点的父亲对应孩子的指针指向N的右孩子，直接删除N结点；

③把N结点的父亲对应孩子的指针指向N的左孩子，直接删除N结点；

④不能直接删除N结点，因为N的两个孩子无处安放，只能用替换法删除。找N左子树的值最大结点R(最右结点)或者N右子树的值最小结点R(最左结点)替代N，因为这两个结点中任意一个的值，与N节点值交换，然后再删除被替换节点。

将删除的情况，用代码给出：

	template<class K>class BSTree{public:typedef BSTNode<K> BSTNode;bool Erase(const K& val){//cur表示将要删除节点，parent为cur的父节点BSTNode* cur = _root;BSTNode* parent = nullptr;//先试着找将要被删的节点，如果最后cur为nullptr，就表示没找到while (cur && cur->_key!= val){if (val < cur->_key){parent = cur;cur = cur->_left;}else if (val > cur->_key){parent = cur;cur = cur->_right;}}//没找到if (cur == nullptr){return false;}//第一种情况：被删节点没有左右孩子else if (cur->_left == nullptr && cur->_right == nullptr){//因为parent == nullptr意味着上面的while循环没进//被删节点是根，且没有左右孩子if (parent == nullptr){_root = nullptr;}//被删节点是父节点左孩子else if (parent->_left == cur){parent->_left = nullptr;}//被删节点是父节点右孩子else{parent->_right = nullptr;}delete cur;return true;}//第二种情况：删除的节点只有左子树else if (cur->_left != nullptr && cur->_right == nullptr){//同上if (parent == nullptr){_root = cur->_left;}else if(parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;return true;}//第三种情况：删除的节点只有右子树else if (cur->_left == nullptr && cur->_right != nullptr){//同上if (parent == nullptr){_root = cur->_right;}else if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;return true;}//与第四种情况：左右都不为空。这里找右树的最左值else{BSTNode* replace = cur->_right;BSTNode* replace_parent = cur;while (replace->_left){replace_parent = replace;replace = replace->_left;}std::swap(replace->_key, cur->_key);//被删除的节点左边肯定没了，但右边有没有还不知道，//不管他有没有直接连接上，哪怕是空if (replace_parent->_left == replace){replace_parent->_left = replace->_left;}else{replace_parent->_right = replace->_right;}delete replace;return true;}return false;}private:BSTNode* _root = nullptr;};

3.在已有数据种查找数据

依旧分为三种情况

1）从根开始比较，查找x（被查找数据），x比根的值大则往右边走查找，x比根值小则往左边走查找。

2）最多查找高度次，走到到空，还没找到，这个值不存在。

3）如果不支持插入相等的值，找到x即可返回。

4）如果支持插入相等的值，意味着有多个x存在，一般要求查找中序的第一个x

将上述三种的情况，用代码给出：

		bool find(const K& val){BSTNode* cur = _root;while (cur){if (val > cur->_key){cur = cur->_right;}else if (val < cur->_key){cur = cur->_left;}else{return true;}			 }//走到空，循环条件不满足执行return false;return false;}

注意搜索二叉树不支持更改节点数据，因为更改节点数据可能会导致整棵树的性质得不到满足。

三、综上完整搜索二叉树代码

包括中序遍历函数InOrder。

#pragma once
#include<iostream>
namespace karsen
{template<class T>struct BSTNode{T _val;BSTNode* _left;BSTNode* _right;BSTNode(const T& val):_val(val),_left(nullptr),_right(nullptr){ }};template<class K>class BSTree{public:typedef BSTNode<K> BSTNode;BSTree() = default;BSTree(const BSTree& t){_root = _Copy(t._root);}BSTree& operator=( BSTree bt){std::swap(_root, bt._root);return *this;}~BSTree(){_Destroy(_root);_root = nullptr;}void InOrder(){_InOrder(_root);std::cout << std::endl;}bool Insert(const K& k){if (_root == nullptr){_root = new BSTNode(k);return true;}else{BSTNode* parent = _root;BSTNode* cur = parent;while (cur){if (k < cur->_val){parent = cur;cur = cur->_left;}else if (k > cur->_val){parent = cur;cur = cur->_right;}else{//不允许插入相等值return false;}}BSTNode* newNode = new BSTNode(k);if (k <= parent->_val){parent->_left = newNode;return true;}else{parent->_right = newNode;return true;}return false;}bool Erase(const K& val){BSTNode* cur = _root;BSTNode* parent = nullptr;while (cur && cur->_val != val){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}}//没找到if (cur == nullptr){return false;}//第一种情况：叶子节点else if (cur->_left == nullptr && cur->_right == nullptr){//根就是叶子if (parent == nullptr){_root = nullptr;}else if (parent->_left == cur){parent->_left = nullptr;}else{parent->_right = nullptr;}delete cur;return true;}//第二种情况：删除的节点只有左子树else if (cur->_left != nullptr && cur->_right == nullptr){//删除根if (parent == nullptr){_root = cur->_left;}else if(parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;return true;}//第三种情况：删除的节点只有右子树else if (cur->_left == nullptr && cur->_right != nullptr){//删除根if (parent == nullptr){_root = cur->_right;}else if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;return true;}//与第四种情况：左右都不为空。找右树的最左值else{BSTNode* replace = cur->_right;BSTNode* replace_parent = cur;while (replace->_left){replace_parent = replace;replace = replace->_left;}std::swap(replace->_val, cur->_val);//被删除的节点左边肯定没了，但右边有没有还不知道，//不管他有没有直接连接上，哪怕是空if (replace_parent->_left == replace){replace_parent->_left = replace->_left;}else{replace_parent->_right = replace->_right;}delete replace;return true;}return false;}bool find(const K& val){BSTNode* cur = _root;while (cur){if (val > cur->_val){cur = cur->_right;}else if (val < cur->_val){cur = cur->_left;}else{return true;}			 }return false;}private:void _InOrder(BSTNode* root){if (root == nullptr)return;_InOrder(root->_left);std::cout << root->_key << ' '<< std::endl;_InOrder(root->_right);}//类似前序BSTNode* _Copy(BSTNode* root){if (root == nullptr)return nullptr;BSTNode* newNode = new BSTNode(root->_val);newNode->_left = _Copy(root->_left);newNode->_right = _Copy(root->_right);return newNode;}void _Destroy(BSTNode*root){if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;}private:BSTNode* _root = nullptr;};
}

四、k/v模型的二叉搜索树

k/v模型的二叉搜索树，相较于普通二叉树搜索树，无非是节点中多出一个成员变量 val 。k/v中的k，指的是key码，充当标签的作用，目的是发挥二叉搜索树的性质；而v即 val 才是真正存储的数据。

	template<class K,class V>struct BSTNode{K _key;V _val;BSTNode* _left;BSTNode* _right;BSTNode(const K& key,const V& val):_key(key),_val(val), _left(nullptr), _right(nullptr){}};

由于是在普通二叉搜索树的基础上，设计出的k/v二叉搜索树，所以k/v二叉搜索树的内部代码与普通二叉搜索树几乎无异。

不同之处有：

①insert插入时，不仅要传key，也要传val。比如模拟翻译字典， “English”是key，那么 “英语” 就是val，其中key与val都是string类型的。

②find搜索到后就返回该节点的指针，没找到则返回nullptr。

③InOrder打印时，要将val的值也打印出。

其他则没什么区别。

下面给出k/v模型二叉树的代码

namespace key_val
{template<class K,class V>struct BSTNode{K _key;V _val;BSTNode* _left;BSTNode* _right;BSTNode(const K& key,const V& val):_key(key),_val(val), _left(nullptr), _right(nullptr){}};template<class K, class V>class BSTree{public:typedef BSTNode<K,V> BSTNode;BSTree() = default;BSTree(const BSTree& t){_root = _Copy(t._root);}BSTree& operator=( BSTree bt){std::swap(_root, bt._root);return *this;}~BSTree(){_Destroy(_root);_root = nullptr;}void InOrder(){_InOrder(_root);std::cout << std::endl;}bool Insert(const K& k,const V& val){if (_root == nullptr){_root = new BSTNode(k,val);return true;}else{BSTNode* parent = _root;BSTNode* cur = parent;while (cur){if (k < cur->_key){parent = cur;cur = cur->_left;}else if (k > cur->_key){parent = cur;cur = cur->_right;}else{//不允许插入相等值return false;}}BSTNode* newNode = new BSTNode(k, val);if (k <= parent->_key){parent->_left = newNode;return true;}else{parent->_right = newNode;return true;}}return false;}bool Erase(const K& key){BSTNode* cur = _root;BSTNode* parent = nullptr;while (cur && cur->_key != key){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}}//没找到if (cur == nullptr){return false;}//第一种情况：叶子节点else if (cur->_left == nullptr && cur->_right == nullptr){//根就是叶子if (parent == nullptr){_root = nullptr;}else if (parent->_left == cur){parent->_left = nullptr;}else{parent->_right = nullptr;}delete cur;return true;}//第二种情况：删除的节点只有左子树else if (cur->_left != nullptr && cur->_right == nullptr){//删除根if (parent == nullptr){_root = cur->_left;}else if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;return true;}//第三种情况：删除的节点只有右子树else if (cur->_left == nullptr && cur->_right != nullptr){//删除根if (parent == nullptr){_root = cur->_right;}else if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;return true;}//与第四种情况：左右都不为空。找右树的最左值else{BSTNode* replace = cur->_right;BSTNode* replace_parent = cur;while (replace->_left){replace_parent = replace;replace = replace->_left;}std::swap(replace->_key, cur->_key);//被删除的节点左边肯定没了，但右边有没有还不知道，//不管他有没有直接连接上，哪怕是空if (replace_parent->_left == replace){replace_parent->_left = replace->_left;}else{replace_parent->_right = replace->_right;}delete replace;return true;}return false;}BSTNode* find(const K& val){BSTNode* cur = _root;while (cur){if (val > cur->_key){cur = cur->_right;}else if (val < cur->_key){cur = cur->_left;}else{return cur;}}return nullptr;}private:void _InOrder(BSTNode* root){if (root == nullptr)return;_InOrder(root->_left);std::cout << root->_key << "->" << root->_val << std::endl;_InOrder(root->_right);}//类似前序BSTNode* _Copy(BSTNode* root){if (root == nullptr)return nullptr;BSTNode* newNode = new BSTNode(root->_key,root->_val);newNode->_left = _Copy(root->_left);newNode->_right = _Copy(root->_right);return newNode;}void _Destroy(BSTNode*root){if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;}private:BSTNode* _root = nullptr;};
}

本文详细介绍了二叉搜索树的概念、性质及实现方法。

读完点赞，手留余香~

查看全文

http://www.dtcms.com/a/521946.html