《基本函数的统一算法》

《基本函数的统一算法》

概要 

本文描述了一种统一的算法，用于在数字计算机上生成三角函数、双曲函数、指数函数、对数函数等基本函数及其反函数。此外，该算法还能执行乘法、除法以及二进制/十进制、十进制/二进制转换。该算法是坐标旋转数字计算机（CORDIC）计算技术的扩展，其特点是采用固定的程序、循环迭代，并且只使用**移位、加法、减法、表查找和位计数**等基本操作。该算法的规整性使其特别适合在只读存储器（ROM）或可编程逻辑阵列（PLA）中实现。

---

简介 

在数字计算机发展的早期，计算基本函数的方法通常依赖于多项式或有理分式逼近。这些方法需要乘法运算，而在早期计算机中，乘法器的硬件实现成本高昂或速度较慢。坐标旋转数字计算机（CORDIC）算法，由 Jack Volder [1] 首次提出，提供了一种替代方案。它通过一系列由移位和加法构成的微旋转来逼近目标角度，从而避免了显式的乘法运算。

Volder 的工作主要集中于三角计算。本文旨在展示如何将 CORDIC 技术**统一和扩展**，使其能够在**圆周、线性、双曲**三种坐标系下运行，并通过同一套硬件架构计算出一大批基本函数。表 I 总结了该统一算法在不同模式和坐标系下所能实现的核心功能。

表 I：统一算法功能摘要**

坐标系	模式	初始值	结果
圆周 (m=1)	旋转	x0=K,y0=0,z0=θx0​=K,y0​=0,z0​=θ	xn=cos⁡θ,yn=sin⁡θ,zn=0xn​=cosθ,yn​=sinθ,zn​=0
	向量化	x0=X,y0=Y,z0=0x0​=X,y0​=Y,z0​=0	xn=X2+Y2,yn=0,zn=tan⁡−1(Y/X)xn​=X2+Y2​,yn​=0,zn​=tan−1(Y/X)
线性 (m=0)	旋转	x0=x,y0=0,z0=yx0​=x,y0​=0,z0​=y	xn=x,yn=0,zn=0xn​=x,yn​=0,zn​=0 (在此过程中，乘积 x⋅yx⋅y 被累积在 yy 寄存器中)
	向量化	x0=x,y0=y,z0=0x0​=x,y0​=y,z0​=0	xn=x,yn=0,zn=y/xxn​=x,yn​=0,zn​=y/x
双曲 (m=-1)	旋转	x0=K′,y0=0,z0=θx0​=K′,y0​=0,z0​=θ	xn=cosh⁡θ,yn=sinh⁡θ,zn=0xn​=coshθ,yn​=sinhθ,zn​=0
	向量化	x0=X,y0=Y,z0=0x0​=X,y0​=Y,z0​=0	xn=X2−Y2,yn=0,zn=tanh⁡−1(Y/X)xn​=X2−Y2​,yn​=0,zn​=tanh−1(Y/X)

*注：K 和 K' 分别为圆周和双曲系统的比例因子常数。*

坐标系统 

CORDIC 算法的统一性体现在参数 mm 上，它定义了三种不同的坐标系：

1. 圆周坐标系 (Circular Coordinate System, m=1)：这是 Volder 原始算法的基础。其微旋转角度为 ei=arctan⁡(2−i)。用于计算正弦、余弦、反正切、模值等。

2. 线性坐标系 (Linear Coordinate System, m=0)：在此模式下，迭代方程退化为简单的移位-累加操作。微旋转被微平移取代，其增量为 ei=2−iei​=2−i。用于实现乘法、除法等基本运算。

3. 双曲坐标系 (Hyperbolic Coordinate System, m=−1)：其微旋转角度基于双曲函数，。用于计算双曲正弦、双曲余弦、指数函数、对数函数等

迭代方程 (Iteration Equations)

统一算法的核心是以下三个迭代方程，它们在每个计算步骤 \( i \) 中同时执行：

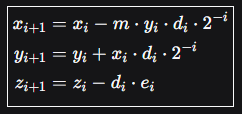
其中：
*   \( m \in \{1, 0, -1\} \) 标识坐标系。
*   \( d_i \in \{+1, -1\} \) 是方向因子。
*   \( e_i \) 是预定义的微角度/值序列，取决于 \( m \)。
*   操作模式决定了 \( d_i \) 的符号：
*   **旋转模式 (Rotation Mode)**：\( d_i = \text{sign}(z_i) \)。目标是驱使残余角度 \( z_i \) 趋于零。
*   **向量化模式 (Vectoring Mode)**：\( d_i = -\text{sign}(y_i) \)。目标是驱使 \( y_i \) 分量趋于零。

---

转换策略 (Conversion Tactics)

为了实现高精度计算，必须解决两个关键问题：**比例因子** 和 **收敛域**。

**1. 比例因子 (Scale Factor)**
在圆周和双曲系统中，每次迭代都会改变向量的模长。可以证明，总比例因子 \( K \) 为：

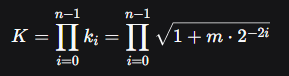
对于圆周系统 (\( m=1 \))，\( K \approx 0.60725 \)。对于双曲系统 (\( m=-1 \))，\( K' \approx 0.82816 \)。处理策略包括：
*   **预缩放 (Prescaling)**：将初始输入 \( x_0 \), \( y_0 \) 乘以 \( 1/K \)。
*   **后缩放 (Postscaling)**：将最终输出乘以 \( 1/K \)。
*   **融合缩放 (Integrated Scaling)**：将缩放操作融入迭代过程，增加额外的迭代步骤。

**2. 收敛域与重复迭代 (Convergence and Repeated Iterations)**
双曲系统 (\( m=-1 \)) 的收敛性需要特别处理。因为序列 \( \arctanh(2^{-i}) \) 的收敛域存在间隙，必须重复特定的迭代索引（例如，i=4, 13, 40, ...）以确保算法对所有有效输入都能收敛。这是该算法实现中的一个关键细节。

---

### **移位器使用 (Shifter Usage)**

CORDIC 算法的效率很大程度上源于对**移位器**的巧妙使用。
*   **常数移位**：在每次迭代 \( i \) 中，移位量 \( 2^{-i} \) 是固定的。这意味着硬件实现时，移位器可以是非常简单的、预定义的连线模式，而不是复杂的桶式移位器。
*   **规整性**：这种“移位-加”的操作序列非常规整，使得算法极易在微代码ROM或硬件状态机中实现。

---

域拓展

通过结合不同坐标系和模式，该统一算法可以计算大量函数。以下是几个典型示例：

*   **计算正弦和余弦**：使用圆周旋转模式，设置 \( x_0 = 1/K, y_0=0, z_0=\theta \)。
*   **计算模和幅角**：使用圆周向量化模式，设置 \( x_0=X, y_0=Y, z_0=0 \)。
*   **计算乘法**：使用线性旋转模式，设置 \( x_0=x, y_0=0, z_0=y \)，结果 \( x \cdot y \) 出现在 \( y_n \) 中。
*   **计算指数**：使用双曲旋转模式，设置 \( x_0=1/K', y_0=0, z_0=a \)，则 \( e^a \approx \sinh a + \cosh a = y_n + x_n \)。
*   **计算自然对数**：使用双曲向量化模式，设置 \( x_0 = w+1, y_0 = w-1, z_0 = 0 \)，则 \( \ln w = 2 \cdot z_n \)。

---

硬件实现 (Hardware Implementation)

CORDIC 算法的硬件架构非常简洁和规整。图 1 展示了一个典型 CORDIC 计算引擎的框图。

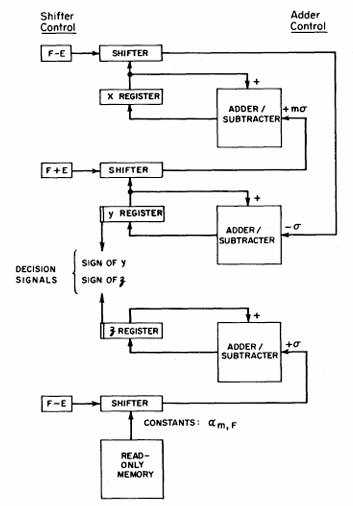
该引擎包含三个主要寄存器（X, Y, Z）和三个功能单元：
1.  **两个移位器**：用于对 Y 和 X 寄存器进行 \( 2^{-i} \) 位的移位。移位量由迭代计数器 \( i \) 控制。
2.  **三个加法器/减法器**：用于根据符号位 \( d_i \) 执行 X, Y, Z 的加/减操作。
3.  **一个只读存储器 (ROM)**：用于存储预先计算好的基本角度/值序列 \( e_i \)。
4.  **一个控制逻辑**：用于生成迭代索引 \( i \)，控制移位量，并根据当前模式（旋转/向量化）和 \( y_i \) 或 \( z_i \) 的符号来决定 \( d_i \)。

工作流程是循环的：
1.  初始化寄存器 \( X, Y, Z \)。
2.  对于 \( i = 0 \) 到 \( n-1 \)：
a. 根据 \( i \) 设置移位量。
b. 从 ROM 中查找 \( e_i \)。
c. 根据模式计算 \( d_i \)。
d. 在一个时钟周期内，并行更新 X, Y, Z 寄存器。
3.  输出最终结果。

这种结构可以实现为**时序型**（一个核心，循环使用）或**流水线型**（多个核心串联，吞吐量极高）。

---

结论 (Conclusion)

本文提出了一种用于计算基本函数的统一算法。该算法是原始 CORDIC 技术的扩展，通过引入坐标系参数 \( m \)，将三角、乘除、双曲等计算统一到同一框架下。其主要优点包括：

1.  **统一性**：同一套硬件可用于计算多种不同函数。
2.  **简洁性**：只需要基本的加、减、移位和表查找操作，无需复杂的乘法器。
3.  **规整性**：算法结构规整，非常适合在 ROM、PLA 或简单的微程序控制中实现。
4.  **效率**：对于 n 位精度，大约需要 n 次迭代，计算速度与软件乘法相当或更快，且硬件成本低。

该算法特别适用于专用计算机、计算器、数字信号处理器以及任何需要高效计算基本函数的嵌入式系统。它为硬件功能单元的设计提供了一种强大而优雅的范式。

[1] Volder, J. E. "The CORDIC Trigonometric Computing Technique." IRE Transactions on Electronic Computers, Vol. EC-8, Sept. 1959, pp. 330-334.