当前位置：首页 > news >正文

从 DeepWalk 到 Node2Vec：如何让图学习“更聪明”？

news 2025/10/24 9:30:08

在图神经网络（GNN）兴起之前，图嵌入（Graph Embedding） 是处理社交网络、知识图谱等复杂结构数据的重要手段。其中，DeepWalk 和 Node2Vec 是两个里程碑式的工作。它们将自然语言处理中的 Word2Vec 思想迁移到图结构中，实现了节点的低维向量表示。

本文将带你深入理解 Node2Vec 的核心思想——为什么它比 DeepWalk 更智能？ 我们将通过手绘图示、数学公式和实际案例，一步步揭示其背后的奥秘。

本文总结:

🔍 一、从 DeepWalk 开始：图上的“词向量”

1.1 DeepWalk 的基本思路

DeepWalk 的灵感来源于 Word2Vec：

把图中的节点看作“词”，把随机游走生成的路径看作“句子”，然后用 Skip-gram 模型训练这些“句子”，得到每个节点的向量表示。

例如，在一个社交网络中：

A → B → C → D → E

这条路径就像一句话：“A 和 B 是朋友，B 和 C 是朋友……”
我们可以通过这个序列来学习 A、B、C 等节点之间的关系。

1.2 DeepWalk 的局限性

然而，DeepWalk 的随机游走是均匀采样邻居节点，即每个邻居被选中的概率相等。这导致了两个问题：

无法控制探索策略：既不能深入局部结构（DFS），也不能广泛探索全局结构（BFS）
信息利用不充分：忽略了节点之间的拓扑距离和上下文关系

👉 这正是 Node2Vec 出现的原因！

🚀 二、Node2Vec：可调的智能游走

2.1 Node2Vec 的核心改进

Node2Vec 在 DeepWalk 基础上做了两大升级：

特性	DeepWalk	Node2Vec
随机游走方式	均匀采样	可控偏置
是否支持 DFS/BFS	否	✅ 支持
参数调节能力	无	有 `p` 和 `q`

✅ Node2Vec 保留了 DeepWalk 的随机游走 + Word2Vec 的训练框架，但引入了搜索偏差（search bias） 来指导游走方向。

🧠 三、Node2Vec 的三大关键设计

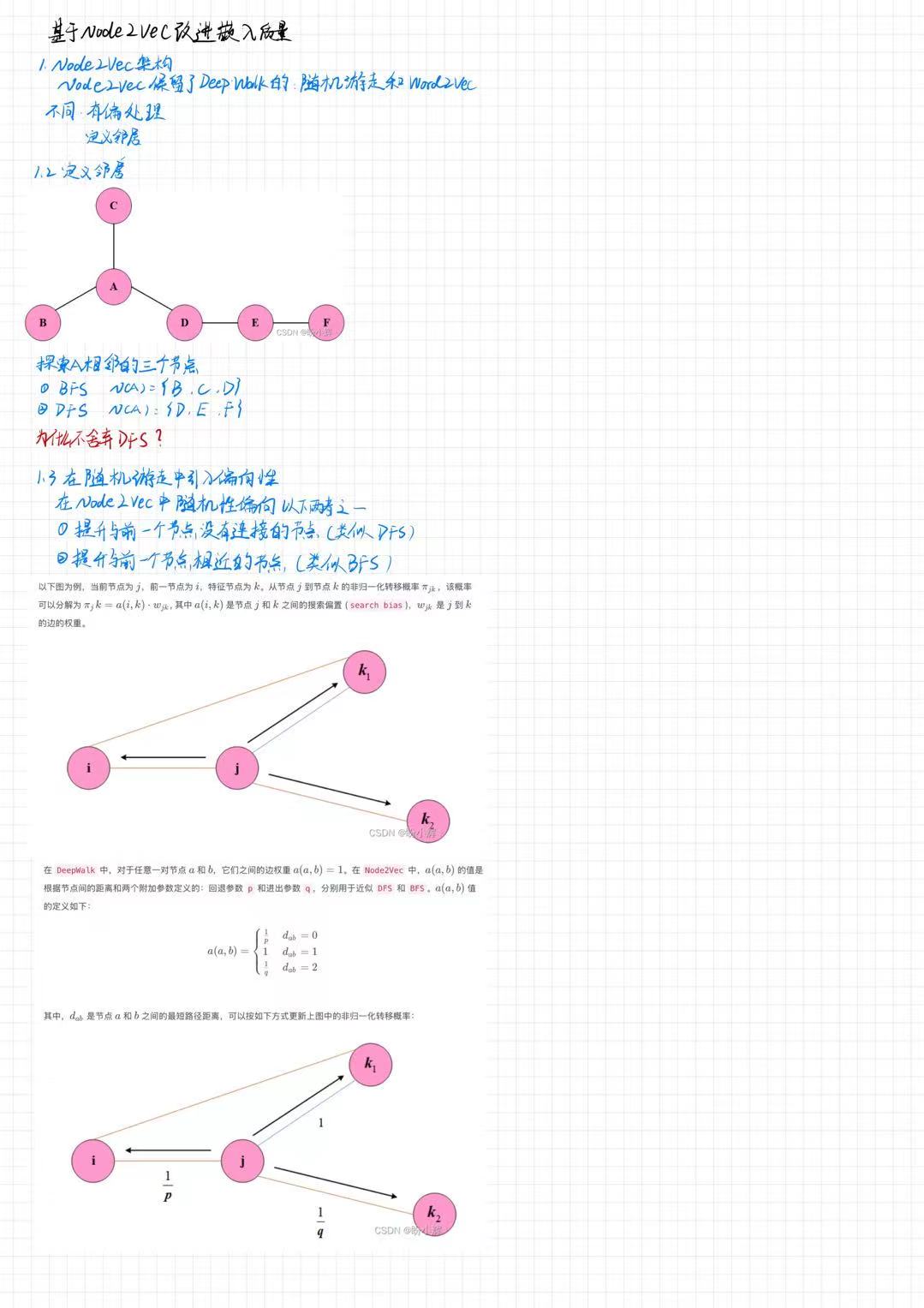
3.1 定义邻域：BFS vs DFS

以如下图为例：

      C|A/ \B   D - E - F

假设当前节点为 A，前一节点为 B。

我们可以定义两种邻域：

BFS 邻域（广度优先）：{B, C, D} —— 包括直接邻居和回退点
DFS 邻域（深度优先）：{D, E, F} —— 沿着一条路径深入探索

⚠️ 但注意：Node2Vec 并不会“选择”某个邻域，而是通过参数调节游走倾向。

3.2 引入搜索偏差：a(i,k)

这是 Node2Vec 的灵魂所在！

核心思想：

当我们在节点 j 上，前一节点是 i，要决定下一步去哪个邻居 k 时，不应该完全随机，而应考虑：
k 是否是前一节点 i？
k 是否靠近 i？
我们希望是“深入探索”还是“广泛扫描”？

为此，Node2Vec 定义了一个非归一化转移概率：

其中：

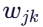：边 (j,k) 的权重（通常为 1）
a(i,k) ：搜索偏差（search bias），取决于 i 和 k 之间的距离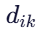

3.3 搜索偏差函数 a(i,k)

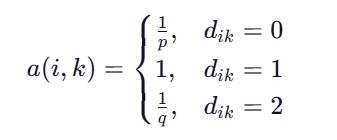
参数含义：

距离	含义	示例
= 0	`k == i`，即回到前一节点	回退
= 1	`k` 是 `j` 的邻居，且不是 `i`	普通邻居
= 2	`k` 是 `j` 的邻居，但与 `i` 不直接相连	探索新区域

参数作用：

参数	作用	效果
`p`（返回参数）	控制是否回退到前一节点	- `p < 1`：鼓励回退 → 类似 DFS - `p > 1`：抑制回退 → 类似 BFS
`q`（进出参数）	控制是否探索远离当前子图的节点	- `q < 1`：倾向于访问远距离节点 → 类似 BFS - `q > 1`：倾向于停留在局部 → 类似 DFS

3.4 图解：非归一化转移概率

以下图为例：

        k₁/  \/    \i ---- j ---- k₂

当前节点：j
前一节点：i
邻居：k₁, k₂

假设：

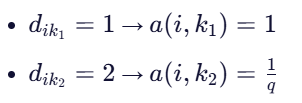
则非归一化概率为：

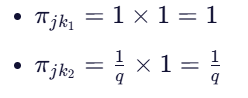
最终归一化后：

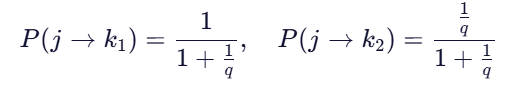
💡 如果 q = 0.5，则 k₂ 的概率更高 → 更愿意探索远方！

🎯 四、为什么 Node2Vec 更强大？

1. 灵活可控的游走策略

p	q	游走风格	适用场景
1	1	随机游走	通用任务
0.5	1	深入局部（DFS）	社区发现、聚类
1	0.5	广泛探索（BFS）	全局结构建模、推荐系统

2. 兼顾局部与全局结构

小 q → 探索更多节点 → 学习全局结构
小 p → 回溯频繁 → 深入局部结构

3. 数学表达清晰，可解释性强

使用 a(i,k) 显式建模了“上下文”对转移的影响
参数直观，便于调参和分析

🧪 五、实战应用建议

任务	推荐参数
社区发现	`p=0.5, q=1`（强调局部结构）
推荐系统	`p=1, q=0.5`（强调全局连接）
图分类	`p=1, q=1`（平衡）

✅ 实际使用中，可通过网格搜索寻找最优 p 和 q。

📚 六、总结：Node2Vec 的本质

Node2Vec 的核心是：让图上的随机游走变得“智能”。

它没有改变 DeepWalk 的整体框架，却通过引入 搜索偏差 和 两个可调参数 p 和 q，实现了对游走行为的精细控制。这使得它既能像 DFS 一样深入挖掘局部社区，也能像 BFS 一样广泛扫描全局结构。

🧩 附录：Node2Vec vs DeepWalk 对比表

特性	DeepWalk	Node2Vec
随机游走方式	均匀采样	偏置采样
是否支持 DFS/BFS	否	✅ 支持
参数调节	无	有 `p`, `q`
局部结构捕捉	一般	强
全局结构捕捉	一般	强
可解释性	低	高

📖 参考资料

Perozzi, B., et al. (2014). "DeepWalk: Online Learning of Social Representations."
Grover, A., & Leskovec, J. (2016). "node2vec: Scalable Feature Learning for Networks."