数据结构10:树和二叉树

简介

前面我们讲到的线性表、队列和栈都是一对一的数据结构，下面我们要讲的树是一种一对多的数据结构----树。
树的严格定义如下：
树：树是n(n=>0)个节点的有限集。 n=0时成为空树。在任意一颗非空树中：（1）有且仅有一个称为根的节点；（2）当n>0时，其余节点可分为m(m>0)个互不相交的有限集T1、T2、T3、Tm，其中每个节点又是一棵树，并且称为根的子树。
树的结构图1所示:

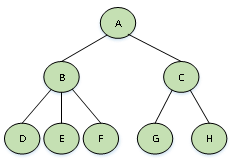
在图1中，A作为树的根节点，它有B和C两个节点；同时B和C也是一颗树，分别有3个和2个节点。
树这种数据结构在实际中有很多的应用，例如文件目录，如图2所示。

二叉树
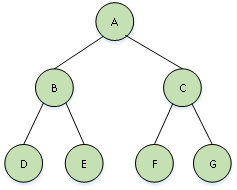
二叉树是一种特殊的树，它的每个节点上最多只能有两个子节点（简称为左孩子和右孩子），它的结构如3所示。A作为根节点，它的左孩子是B，右孩子是C；同时B和C也都是一棵树，D、E和F、G分别是它们的孩子。二叉树较为简单，并且易于理解，我将它作为重点，进行详细讲解。

二叉树中的术语

结点度：节点所拥有的孩子的个数成为该节点的度，在二叉树中度的取值只能是0,1,2。图3中A、B、C它们的度为2，D、E、F、G的度为0。
叶节点：度为0的节点成为叶结点或终端结点。图3中，D、E、F、G都为终端节点。
左孩子、右孩子、双亲：树中一个结点的子树的根结点称为这个结点的孩子。这个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。在图3中，D是B左孩子，E是B的右孩子，B是D和E的双亲，D和E互为兄弟。
结点的层数：规定树的根结点的层数为1，其余结点的层数等于它的双亲结点的层数加1。在图3中，A的层数为1，B的层数为2，D的层数为3。
树的深度：树中所有结点的最大层数称为树的深度。图3中的树就是一个深度为3的树。
满二叉树：在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的一棵二叉树称作满二叉树。图3中的树就是一棵满二叉树。
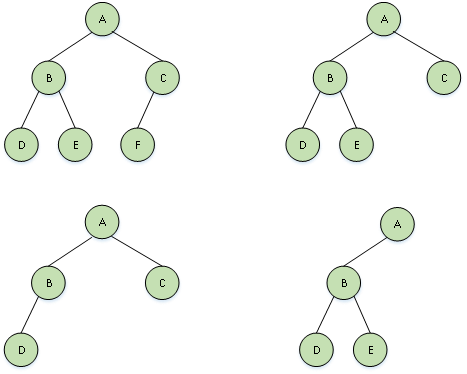
完全二叉树：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为 i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。完全二叉树的特点是：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。完全二叉树如图4所示。

二叉树的性质

1：二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
2：深度为k的二叉树至多有2{k}-1个结点(k≥1)。
3：包含n个结点的二叉树的高度至少为log2(n+1)。
4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。

本节主要介绍了树的和二叉树的基本概念，并对二叉树中的术语和性质进行了简单的介绍。在下一章节中，我们将对二叉树的遍历方式、数据结构和API函数进行介绍。