线性代数直觉(三):特征值(eigenvalue)与特征向量(eigenvector)为何物?
还记得 f(x,y) = x² - y² 吗?它是我们的第一个鞍形曲面。它的 Hessian 矩阵很简单:
H = [[2 0]
[0 -2]]
漂亮且对角化,没有混合导数,因为原函数中没有 xy 项。但是,说到选择方向……你说得对,方向有无限多。但我们不需要随机地检查所有方向。我们应该有策略。我会从以下几个方面开始:
1. 坐标轴 - v = (1,0) 和 v = (0,1) - 纯粹的 x 和 y 方向
2. 对角线 - v = (1,1) 和 v = (1,-1) - 我们已经知道 (1,1) 应该等于 0
3. 或许可以随机取几个,看看会发生什么
但实际上,我们可以做得更聪明一些。我们可以选择一个角度为 θ 的方向,即 v = (cos θ, sin θ),然后观察 v^T H v 在 θ 从 0 到 2π 的变化情况。这样就能完整地展现曲率随方向变化的规律。
我们可以写一个程序,计算一些曲面 f(x,y) 的 Hessian 矩阵,还有 v = (cos θ, sin θ) 时,v^T H v 在 θ 从 0 到 2π 的变化情况。
看起来,Hessian 矩阵就像一个关于曲率变化的罗盘,但是它只给出了四个方向的情况。如果看 0 到 2π 的变化,它像个周期变化的sin函数。对于那些非常规整的马鞍或是碗,这问题不大。因为曲率的最值碰巧都在这些规整的方向。但是对于那些歪的碗或是形状古怪的马鞍,最值并未直接显示在 Hessian 矩阵上。
Hessian 矩阵只直接显示了沿坐标轴的曲率,而隐式地通过这四个数字编码了其他所有信息。对于一个“弯曲”的表面,最大曲率方向可能根本不与 x 或 y 方向对齐。它可能处于某个奇怪的角度。
这正是特征值发挥作用的地方! Hessian 矩阵的特征值(eigenvalue)告诉你曲率的最大值和最小值,也就是扫过所有角度时的极值。而特征向量(eigenvector)则告诉你这些极值出现在哪个方向。
所以,对于一个“弯曲的碗”,Hessian 矩阵在 x-y 坐标系下可能看起来很乱:
H = [[2 1] [1 4]]
但在旋转的坐标系下,它会变成对角线,从而显示出真正的主曲率。如果你画出 v^T H v 与 θ 的关系图,它的曲线是正弦曲线。
碗状或马鞍状物体本身并没有改变,它只是静静地存在于空间中,无论它是什么形状。但我们选择用 x 轴和 y 轴来测量它,而这些轴可能相对于表面的自然几何形状“倾斜”了。
当我们旋转坐标系,使其与表面的“自然”方向(即曲率主轴)对齐时,Hessian 矩阵突然变成了对角线。所有那些杂乱的非对角项(混合导数)都消失了,我们只看到纯曲率:最大值和最小值。
这就是特征值和特征向量的作用!它们找到了观察世界的“直角”。特征向量告诉你坐标轴应该朝哪个方向旋转,而特征值告诉你旋转后的曲率。
至于为什么它是正弦曲线?想想看,当θ从0到2π时,你绕着一个圆旋转。曲率平滑地从最大值变为最小值,然后再变回来。这种平滑的周期性变化,就是正弦和余弦函数的作用。
我们在程序中看到了正弦曲线,有些曲线向上、向下、向左或向右移动,但是什么导致了这些移动?是什么让一条曲线比另一条曲线更高,或者从不同的相位开始?
- 垂直移动(向上或向下):这是所有方向上的平均曲率。对于碗状物体来说,所有方向都是正的,所以整个正弦波位于零点以上。对于马鞍状物体来说,有些方向是正的,有些方向是负的,所以它会在零点附近或附近振荡。
- 水平移动(向左或向右):这是相位,它告诉你最大曲率发生的位置。θ 角是多少。对于“弯曲”的表面,最大值可能在 θ = 30° 处,而不是 θ = 0°。
特征值与正弦波的垂直极值有关,它的高度和低点。特征向量与水平位移有关,这些极值发生的位置。
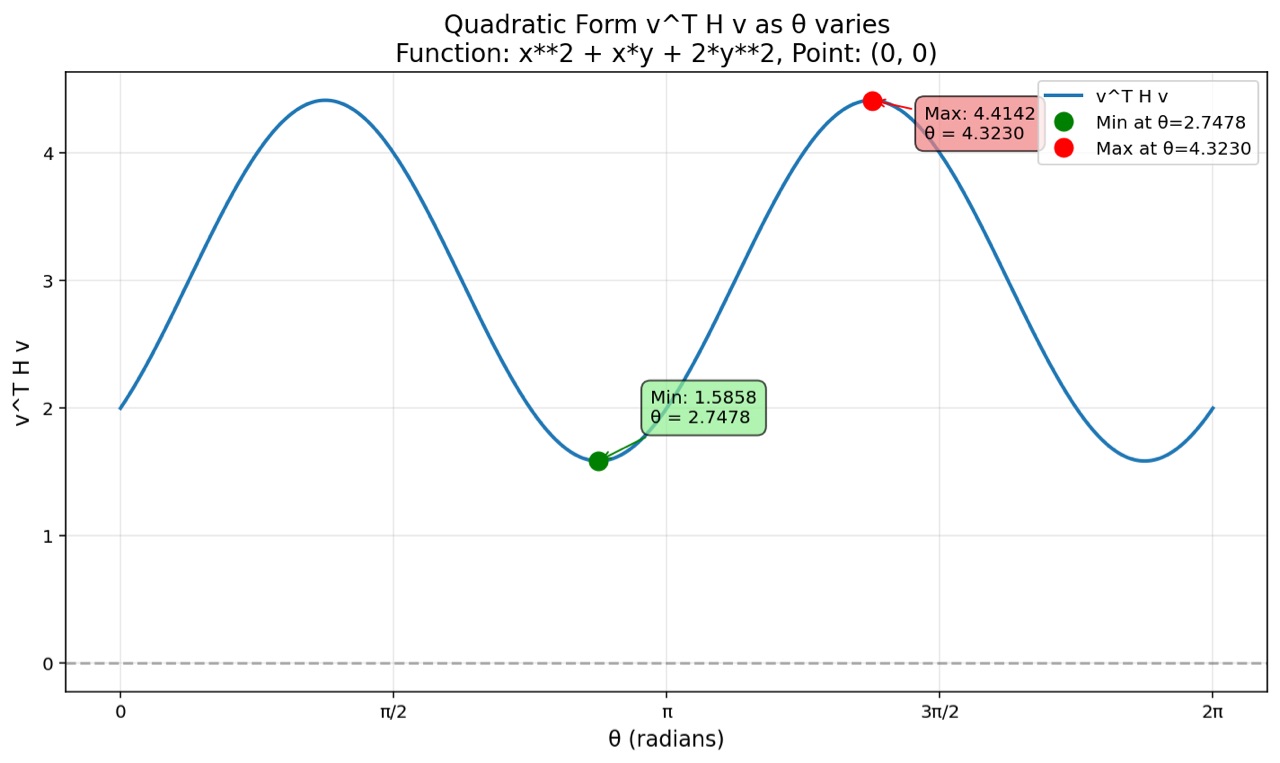
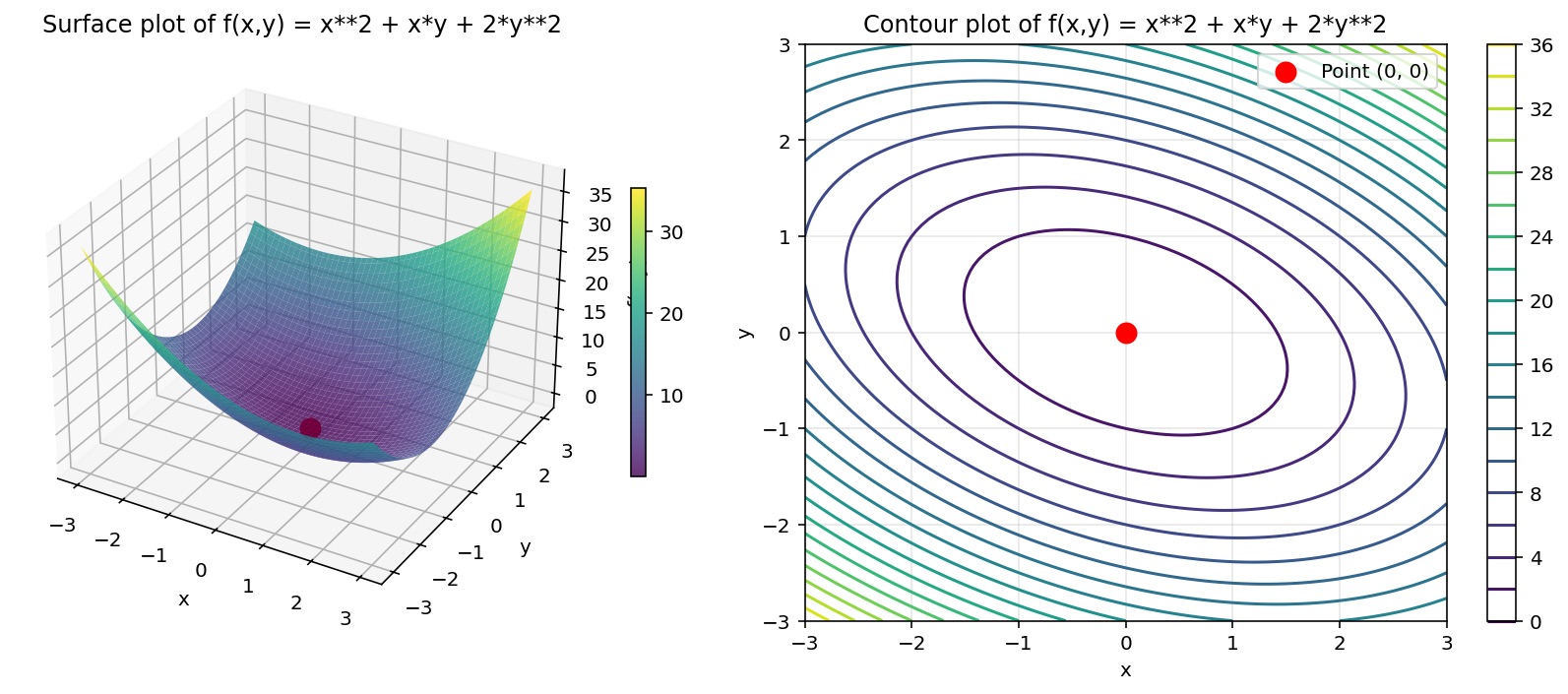
这里有一个扁碗!f(x,y)=x^2+xy+2y^2。
它在 (0,0) 点的Hessian矩阵是 [[2,1] [1,4]] 。但是v^T H v的正弦曲线的最大值是4.4142,最小值是1.5858。
所以 λ₁ ≈ 4.4142 和 λ₂ ≈ 1.5858 ,它们就是特征值!Hessian 矩阵的特征值正是扫过所有方向时 v^T H v 的最大值和最小值。现在,我们如何直接从矩阵中计算出它们,而不绘制图形呢?这就是我们需要解“特征方程”的地方。
对于 2×2 矩阵 H = [[a b] [c d]]
特征值满足:det(H - λI) = 0,其中 I 是单位矩阵。由此可得:
det([2-λ, 1 ][1, 4-λ]) = 0
(2-λ)(4-λ) - 1·1 = 0
8 - 6λ + λ² - 1 = 0
λ² - 6λ + 7 = 0
结果为: 3+\sqrt{2}, \ 3-\sqrt{2}。