当前位置：首页 > news >正文

希尔排序详解

news 2025/10/23 11:05:19

前言：我们之前了解直接插入排序，知道如果待排序数组越有序的话，则直接插入排序的时间效率越高，直接插入排序慢就慢在如果小的数在后面大的数在前面则每一个数要移动很多项，如果能够让大的数基本都在后面，小的数基本都在前面则大大提高直接插入排序的时间效率。那我们今天的希尔排序便是从这个视角优化直接插入排序而演变出来的。

希尔排序

算法思想：先选定一个整数gap，将待排序的序列按照按照gap的距离分成若干分组，并对每一组数进行直接插入排序，然后gap=gap/3+1得到下⼀个整数gap，再次分组排序，直到gap=1再进行最后一次直接插入排序，得到排序好的新序列

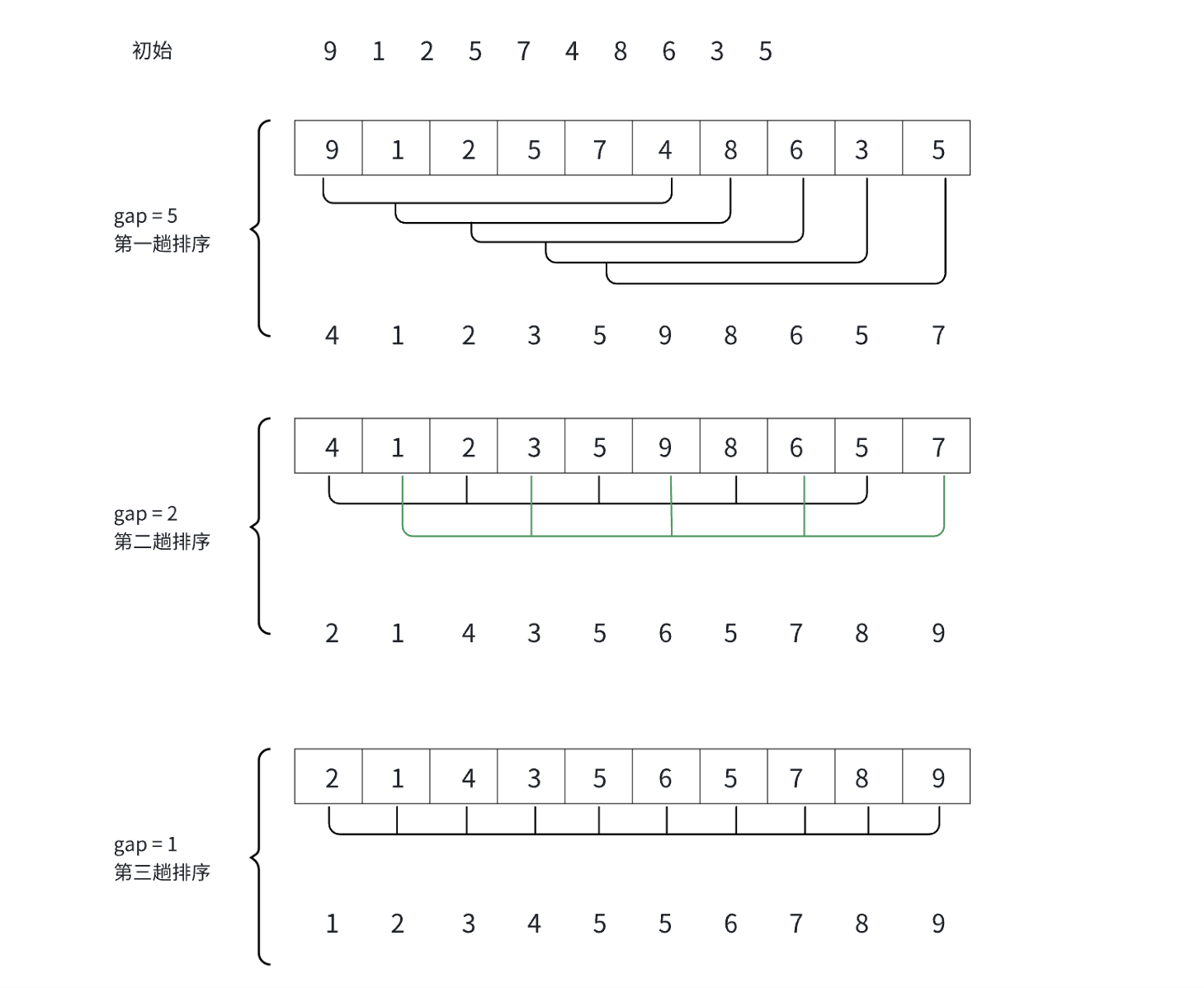
在这里插入图片描述
gap>1都是预排序目的是让序列更趋近于有序化（即小的在前大的在后），当gap==1时序列已经接近有序最后再整体直接插入排序使得有序化

希尔排序正是将我们先要排序得序列先分成一个个小的部分，但是增加排序序列个数，并最后形成较为有序得序列并运用直接插入排序形成新的有序序列，所以希尔排序也被称为缩小增量法。

希尔排序动态图

在这里插入图片描述

代码实现

void ShellSort(int arr[],int size)
{int gap = size;int temp = 0;int end = 0;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < size - gap; i++){end = i;temp = arr[end +gap];while (end >= 0){if (arr[end] > temp){arr[end + gap] = arr[end];end = end - gap;}else{break;}}arr[end + gap] = temp;}}}

希尔排序代码详解

第一部分：

for (int i = 0; i < size - gap; i++){end = i;temp = arr[end +gap];while (end >= 0){if (arr[end] > temp){arr[end + gap] = arr[end];end = end - gap;}else{break;}}arr[end + gap] = temp;}

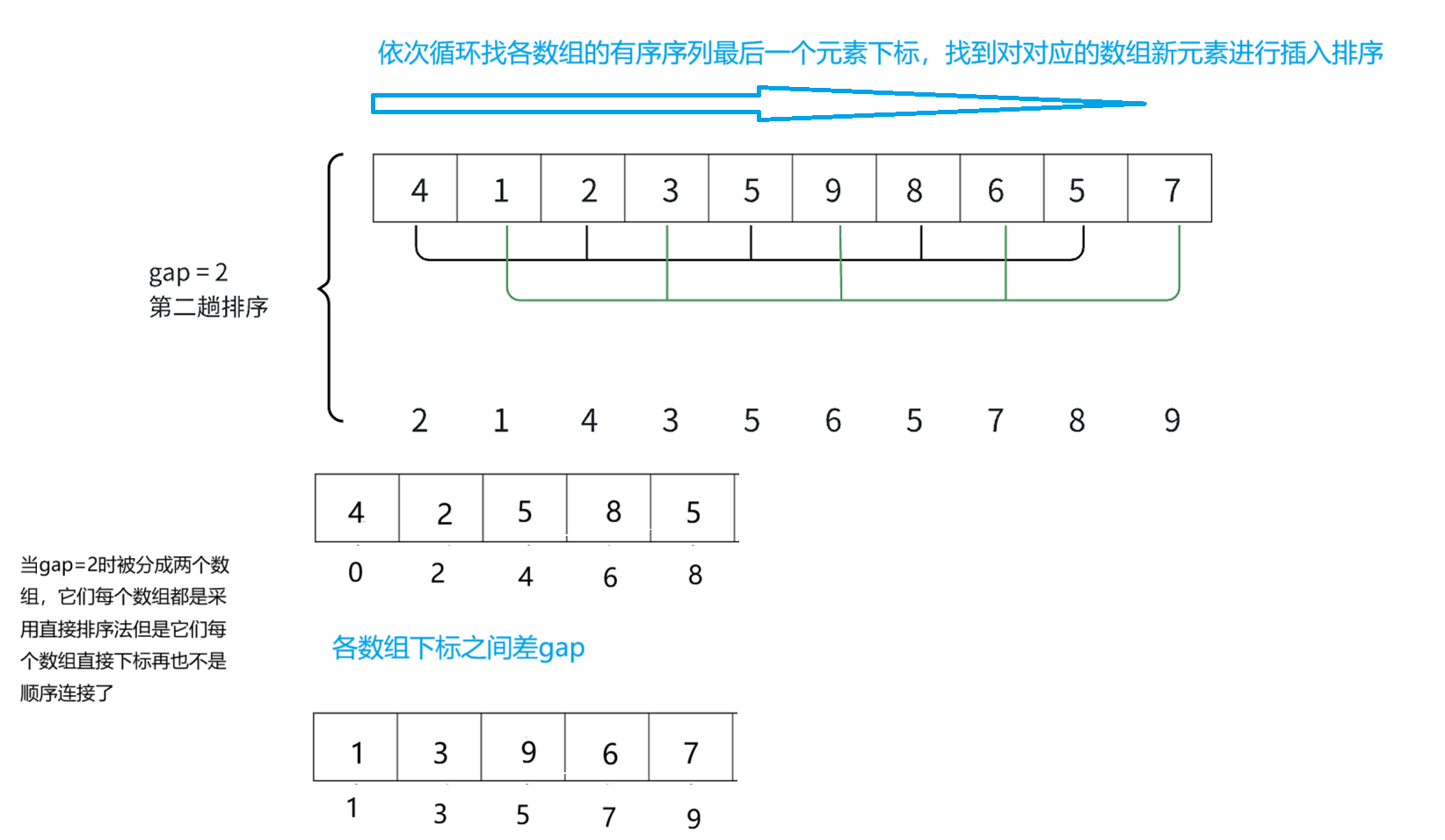
在这里插入图片描述

以gap将序列分成多个序列，在每一个分组中我们都用到直接插入排序，我们for (int i = 0; i < size - gap; i++)依次找到各数组有序序列最后一个元素下标，并将待插入元素插入其中。其最后一个有序序列的元素下标为n-gap-1所以循环结束条件为i < size - gap。

关于最后循环条件i < size - gap的特别说明：
最后一个数组元素就是最后一个要插入的数据，所以最后一个数要插入的分割数组的有序序列下标即为最后一个有序序列的尾部即n-gap-1(下标)，在图中即为元素6对应的下标。

第二部分：

while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < size - gap; i++){......}}

这部分主要将是依次调整各分割出来的数组之间的距离，让距离逐渐减小。gap = gap / 3 + 1的设置保证了gap最后能取到1从而进行最后的整个数组的直接插入排序，从而使数组有序。并在再次为1是不满足gap>1从而跳出循环。（gap也可以取gap = gap / 2 + 1）

希尔排序的时间复杂度计算

外层循环：

while (gap > 1){gap = gap / 3 + 1;	......}

外层时间复杂度为O(log~2~n)（gap = gap / 2 + 1）或者O(log~3~n)（gap = gap / 3 + 1），即O（logn）

内层循环：

for (int i = 0; i < size - gap; i++){end = i;temp = arr[end +gap];while (end >= 0){......}arr[end + gap] = temp;}

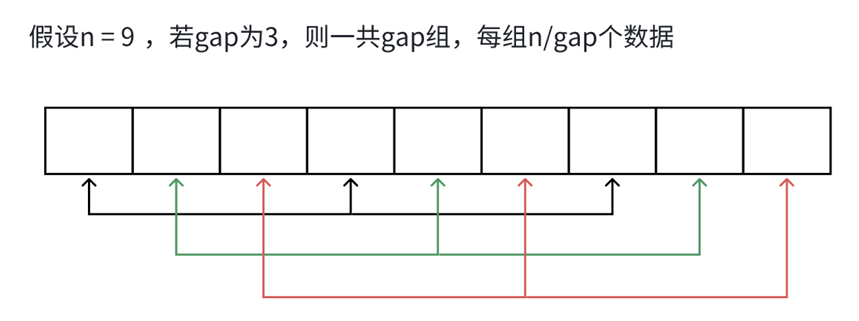
在这里插入图片描述
假设⼀共有n个数据，合计gap组，则每组为 $ngap{n\over gap}$ 个；在每组中，插⼊移动的次数最坏的情况下为gap*[1 +2+3+…+( $ngap{n\over gap}$ -1)]
gap取值有（以除3为例）： $n3{n\over 3}$ $n9{n\over 9}$ $n27{n\over 27}$ … 2 1

当当gap为 $n3{n\over 3}$ 时，移动总次数为 $n3{n\over 3}$ *（1+2）= n
当gap为 $n9{n\over 9}$ 时，移动总数为： $n9{n\over 9}$ *(1 +2+3+…+8) = $n9{n\over 9}$ * $8(1+8)2{8(1+8)\over 2}$ = 4n
最后一趟，gap=1即直接插⼊排序，内层循环排序消耗为n
通过上面的分析，我们可以画出下面的曲线

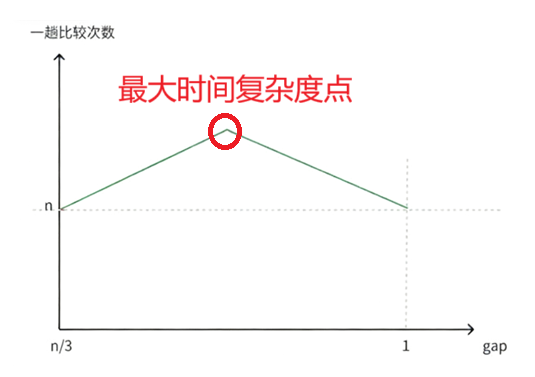
因此，希尔排序在最初和最后的排序的次数都为n，即前⼀阶段排序次数是逐渐上升的状态，当到达某⼀顶点时，排序次数逐渐下降⾄n，⽽该顶点的计算暂时⽆法给出具体的计算过程

对这个图像的分析：
一开始的增大时由于随着gap的减小for (int i = 0; i < size - gap; i++)这个循环次数变多，而由于刚开始数组还没有很大的有序化while (end >= 0)的循环次数改变还不明显，所以一开始逐渐增加，但随着数组逐渐有序化while (end >= 0)的循环开始减小，虽然for (int i = 0; i < size - gap; i++)还是增加，但总体呈现下降趋势。