数据库（6）

目录

树和森林

一、二叉树还原为森林

二、树和森林的存储方式

1、双亲表示法

2、孩子表示法

3、孩子兄弟表示法

4、总结

三、关系结构图

树和森林

一、二叉树还原为森林

方法：把最右边的子树变为一棵树，其余右子树为兄弟

二叉树还原为森林的核心是拆分 “右指针串联” 的根节点，并将每棵子二叉树还原为普通树。具体步骤基于森林转二叉树的逆过程：

1、拆分根节点的右子树：从二叉树的根节点开始，沿右指针依次拆分出所有 “子根节点”（每个子根对应原森林中一棵树的根）。例如，若二叉树根节点 A 的右指针指向 E，E 的右指针指向 F，则拆分出 A、E、F 三个子根，分别对应森林中的三棵树。

2、单棵二叉树还原为普通树：对每个拆分出的子根对应的二叉树，按 “左孩子为原树孩子，右孩子为原树兄弟” 的规则还原：

（1）节点的左子树保留为原树的 “第一个孩子”；

（2）节点的右子树（及右子树的右子树）均视为原节点的 “兄弟”，需将这些右子树节点转为原节点的直接兄弟（即同一父节点的孩子）。

3、所有还原后的普通树共同组成原森林。

二、树和森林的存储方式

1、双亲表示法

定义：以 “节点 - 父节点” 的映射关系存储树或森林，每个节点记录其双亲（父节点）的位置，根节点的双亲标记为特殊值（如 - 1）。

结构设计：

• 用数组存储所有节点，每个元素包含两部分：节点值、父节点索引（数组下标）。

• 示例（树结构：A 是根，孩子 B、C；B 的孩子 D）：

  索引	节点值	父节点索引
  0	A	-1（根）
  1	B	0（父为 A）
  2	C	0（父为 A）
  3	D	1（父为 B）

特点：

• 优点：查询节点的双亲效率高（O (1)），适合 “向上追溯” 场景（如找祖先）。
• 缺点：查询节点的孩子需遍历整个数组（O (n)），不适合频繁访问孩子的操作。
• 适用场景：森林（多棵树）存储（只需为每棵树根节点标记父节点为 - 1），或需频繁查找父节点的场景。

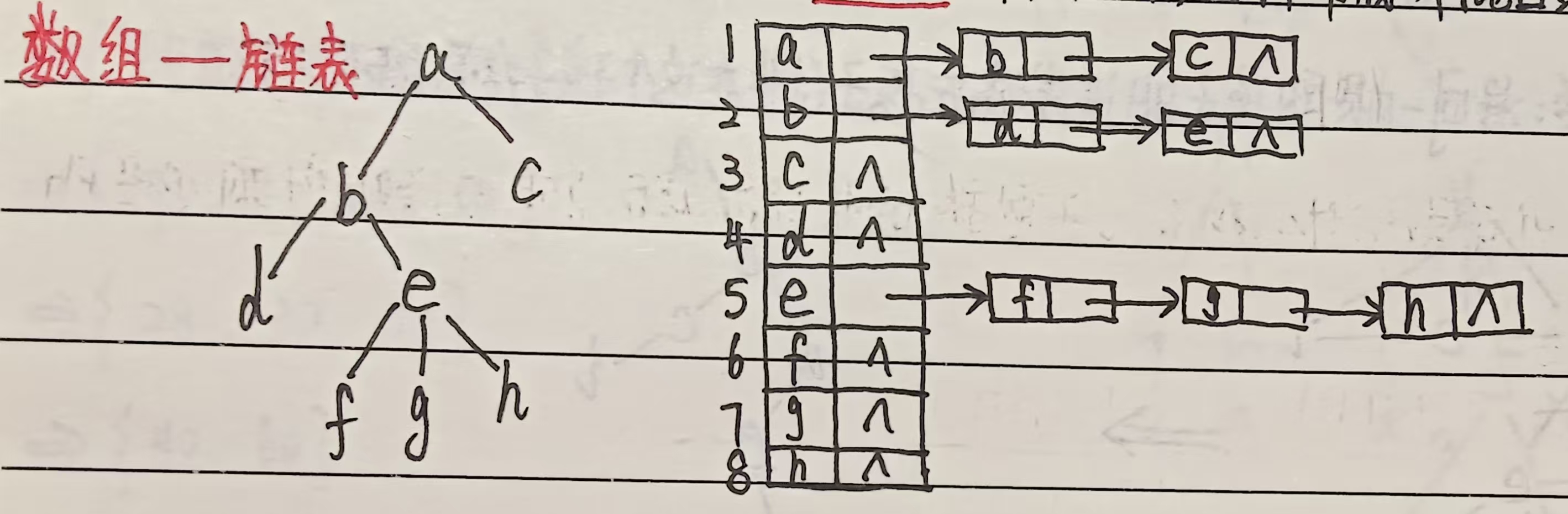
2、孩子表示法

定义：以 “节点 - 孩子列表” 的映射关系存储树或森林，每个节点记录其所有直接孩子的位置，形成 “父节点指向孩子集合” 的结构。

结构设计：

• 主数组存储所有节点，每个元素包含：节点值、指向孩子链表的指针。

• 孩子链表：每个节点的所有直接孩子按顺序组成链表（便于动态增删孩子）。

• 示例（同上树结构）：

  主数组：
  [A -> [B, C],  B -> [D],  C -> [],  D -> []]
  （A的孩子链表为B→C，B的孩子链表为D，C和D无孩子）
  

特点：

• 优点：查询节点的所有孩子效率高（直接遍历链表），适合 “向下访问” 场景（如遍历子树）。
• 缺点：查询节点的双亲需遍历所有节点的孩子链表（O (n)），结构较复杂（需维护数组和链表）。
• 适用场景：单棵树或森林中需频繁访问孩子的场景（如树的层次遍历）。

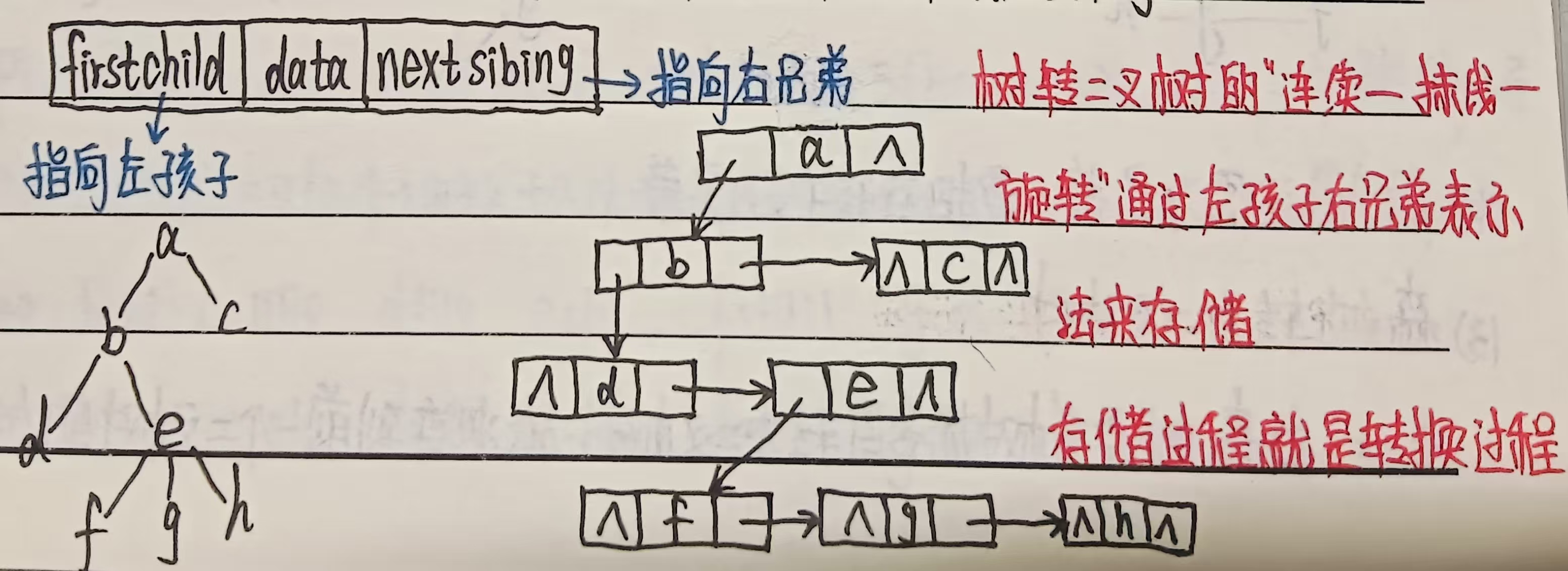
3、孩子兄弟表示法

定义：又称 “二叉树表示法”，通过二叉树的结构存储树或森林：每个节点包含三个部分 —— 节点值、指向第一个孩子的指针（左指针）、指向第一个兄弟的指针（右指针）。

结构设计：

• 节点 =（值，左孩子指针，右兄弟指针）。
• 规则：
  • 左指针：指向节点的第一个直接孩子；
  • 右指针：指向节点的下一个兄弟节点（同一父节点的其他孩子）。
• 示例（同上树结构）：

  A的左指针→B（第一个孩子），A的右指针→null（无兄弟）；  
  B的左指针→D（第一个孩子），B的右指针→C（下一个兄弟）；  
  C的左指针→null，C的右指针→null；  
  D的左指针→null，D的右指针→null。  
  

特点：

• 优点：结构简洁（仅用两个指针），可直接复用二叉树的操作算法（如遍历、插入），同时支持树和森林的存储（森林可通过根节点的右指针串联，如森林中树 T1 的根右指针→T2 的根）。
• 缺点：理解较抽象（右指针表示兄弟而非右孩子），查询节点的所有兄弟需沿右指针遍历。
• 适用场景：树与二叉树的转化（核心存储方式）、需统一树和森林操作逻辑的场景（如编译器的语法树）。

4、总结

三种存储方式各有侧重：

• 双亲表示法：高效查父，适合向上追溯；
• 孩子表示法：高效查子，适合向下遍历；
• 孩子兄弟表示法：结构灵活，是树与二叉树转化的桥梁，适用范围最广。实际应用中需根据操作需求（查父 / 查子 / 转化）选择合适的存储方式。

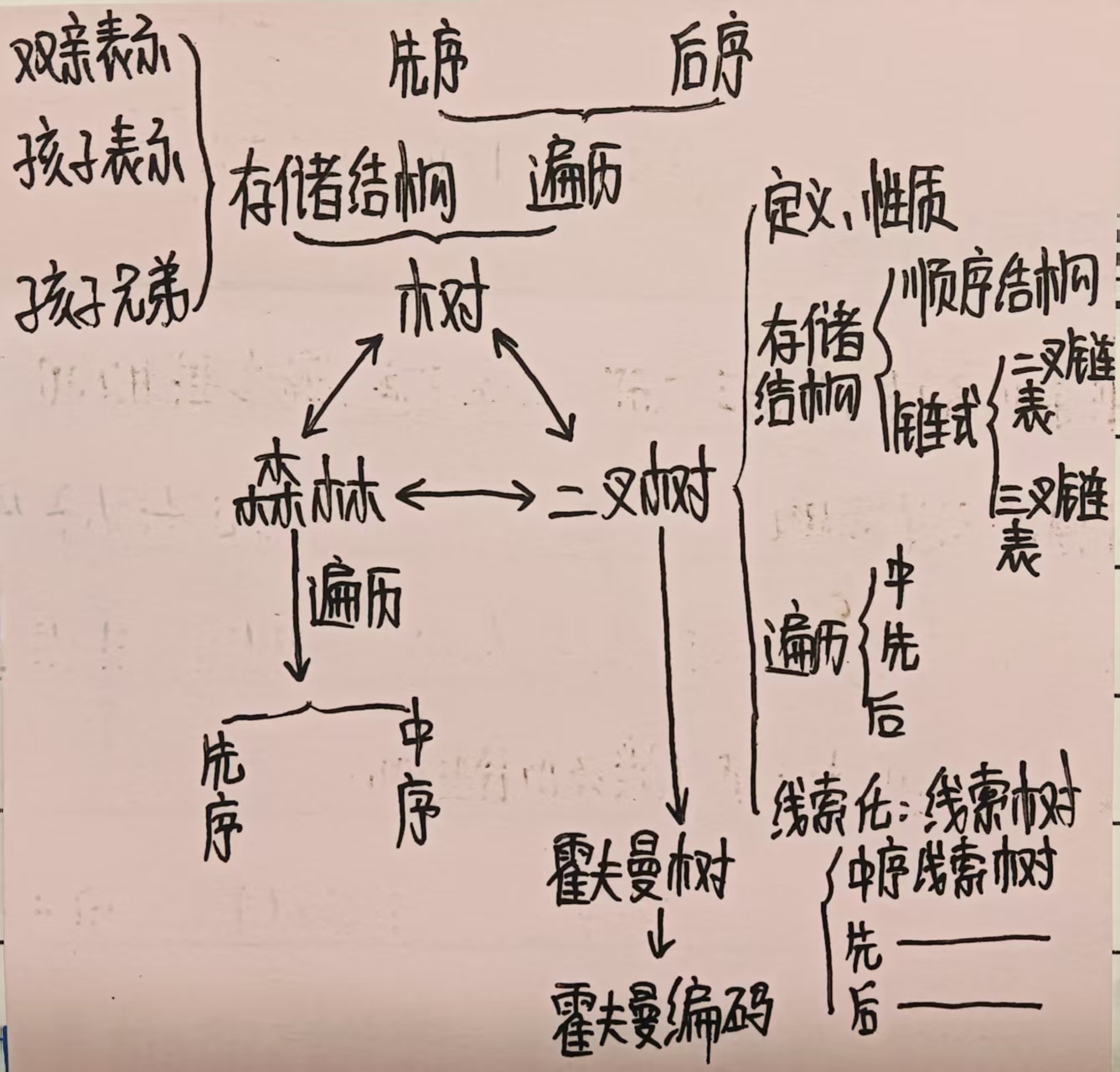
三、关系结构图