R语言：非平稳时间序列实例

install.packages("astsa") library(astsa) # 加载JJ数据 data(jj) # 查看数据结构 str(jj)

（a）绘制时间序列图并解释特征

# 绘制时间序列图 plot(jj, main = "强生公司1960-1980年季度每股收益时间序列",      xlab = "年份", ylab = "每股收益")

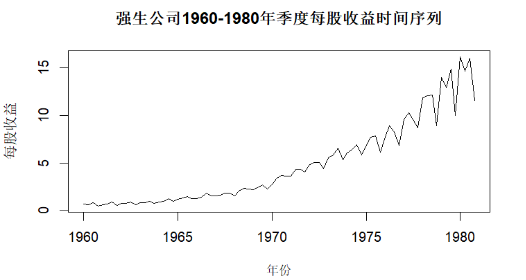
特征：由图可知，强生公司每股收益的季度数据的时间序列呈现指数增长趋势，且季度间存在季节性波动，方差随时间增大，存在异方差性。

（b）确定 Box-Cox变换的最优 λ 值

# 计算最优λ（对数似然和信息准则） lambda_jj <- BoxCox.lambda(jj) cat("最优λ值为：", lambda_jj, "\n")

library(MASS) data(jj) # 绘制对数似然曲线（幂变换） boxcox(jj ~ 1, lambda = seq(-2, 2, 0.1),        main = "Box-Cox变换的对数似然曲线",        xlab = "λ值", ylab = "对数似然值") # 标记最优λ lambda_opt <- boxcox(jj ~ 1, lambda = seq(-2, 2, 0.01))$x[which.max(boxcox(jj ~ 1, lambda = seq(-2, 2, 0.01))$y)] abline(v = lambda_opt, col = "red", lty = 2)  # 最优λ位置画竖线 text(lambda_opt, max(boxcox(jj ~ 1)$y), paste0("最优λ≈", round(lambda_opt, 2)), col = "red")

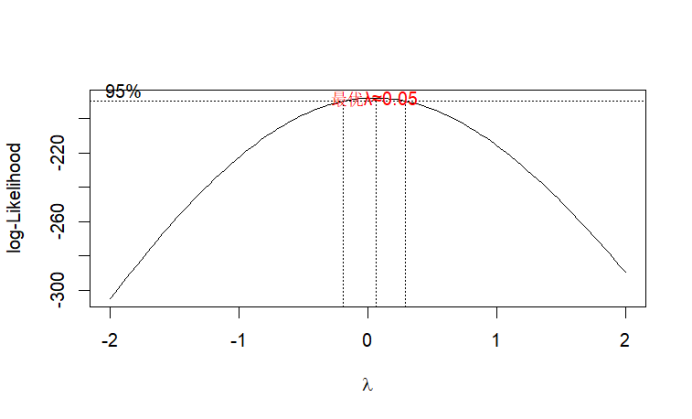
（c）基于最优λ的Box-Cox变换及平稳性分析

library(forecast)  # 用于Box-Cox变换 library(tseries)   # 用于ADF平稳性检验 library(astsa)     # 加载内置JJ数据 # 1. 加载数据并确定最优λ data(jj)  # 强生公司季度收益数据（1960Q1-1980Q4） lambda_opt <- BoxCox.lambda(jj, method = "loglik")  # 用对数似然法计算最优λ cat("Box-Cox变换最优λ值：", round(lambda_opt, 3), "\n") # 2. 执行Box-Cox变换 if (abs(lambda_opt) < 1e-6) {  # 若λ接近0，直接用对数变换（避免数值问题）   jj_transformed <- log(jj)   transform_note <- "使用对数变换（λ≈0）" } else {   jj_transformed <- (jj^lambda_opt - 1) / lambda_opt  # 通用幂变换公式   transform_note <- paste0("使用幂变换（λ=", round(lambda_opt, 3), "）") } # 3. 转换为时间序列对象 jj_transformed_ts <- ts(   jj_transformed,   start = start(jj),  # 继承原始数据的起始时间（1960Q1）   frequency = frequency(jj)  # 季度数据，frequency=4 ) # 4. 绘制变换后的时间序列图（对比原始序列） par(mfrow = c(2, 1), mar = c(4, 4, 2, 1))  # 分两栏绘图 plot(jj, main = "原始JJ季度收益序列", xlab = "年份", ylab = "收益") plot(jj_transformed_ts, main = paste("变换后JJ季度收益序列（", transform_note, "）"),      xlab = "年份", ylab = "变换后收益") par(mfrow = c(1, 1))  # 恢复绘图布局

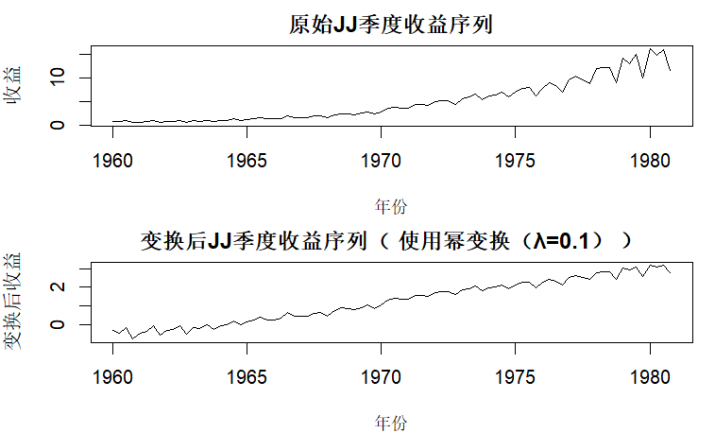
# 5. 平稳性检验（ADF检验） adf_result <- adf.test(jj_transformed_ts) cat("\n变换后序列的ADF平稳性检验结果：\n") print(adf_result)

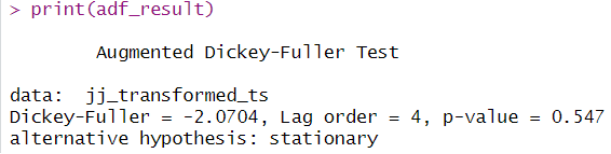
平稳性解读：在5%显著性水平下，变换后序列仍为非平稳，需要进一步差分。

（d）对数差分、时序图、平稳检验

# 1. 复用前文数据与最优λ data(jj) lambda_opt <- BoxCox.lambda(jj, method = "loglik")  # 最优λ # 执行Box-Cox变换 jj_transformed <- if (abs(lambda_opt) < 1e-6) log(jj) else (jj^lambda_opt - 1)/lambda_opt jj_transformed_ts <- ts(jj_transformed, start = start(jj), frequency = 4) # 2. 差分处理 # 一阶差分（消除趋势） jj_diff1 <- diff(jj_transformed_ts)  # 一阶差分序列 # 若存在季节性，补充季节差分（季度数据，滞后4期） jj_diff_seasonal <- diff(jj_transformed_ts, lag = 4)  # 季节差分序列 # 综合差分 jj_diff_combined <- diff(jj_diff_seasonal)  # 一阶差分后再季节差分 # 3. 差分序列可视化（对比原始变换序列） par(mfrow = c(2, 2), mar = c(3, 3, 2, 1), mgp = c(1.5, 0.5, 0)) plot(jj_transformed_ts, main = "变换后序列", ylab = "") plot(jj_diff1, main = "一阶差分序列", ylab = "") plot(jj_diff_seasonal, main = "季节差分序列（滞后4）", ylab = "") plot(jj_diff_combined, main = "一阶+季节差分序列", ylab = "") par(mfrow = c(1, 1))  # 恢复布局

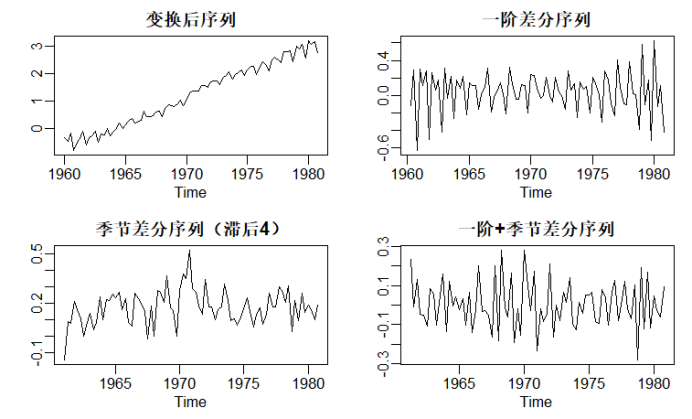
# 4.差分后序列的平稳性检验 adf_diff1 <- adf.test(jj_diff1) cat("一阶差分序列ADF检验结果：\n") print(adf_diff1) if (adf_diff1$p.value < 0.05) {   cat("结论：一阶差分后序列在5%水平下平稳。\n")   chosen_diff <- jj_diff1  # 选定一阶差分序列进行后续分析 } else {   cat("结论：一阶差分后仍非平稳，建议使用综合差分。\n")   chosen_diff <- jj_diff_combined }

# 5. 通过ACF/PACF识别ARMA模型阶数 par(mfrow = c(1, 2), mar = c(3, 3, 2, 1)) acf(chosen_diff, main = "差分序列ACF", lag.max = 20)  # 自相关函数 pacf(chosen_diff, main = "差分序列PACF", lag.max = 20)  # 偏自相关函数 par(mfrow = c(1, 1))

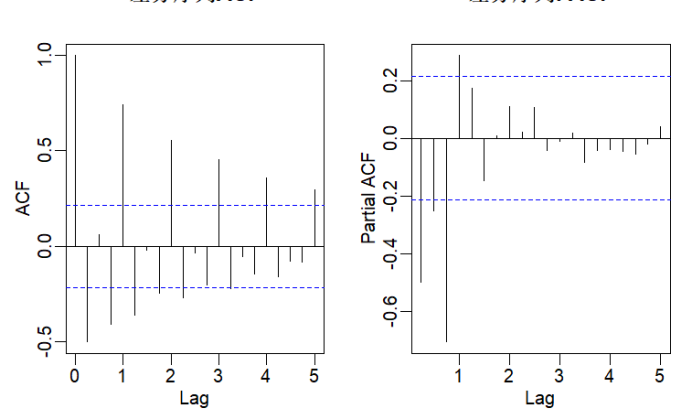
模型识别：

1. 若ACF在滞后q期截断，PACF拖尾 → 选MA(q)模型；
2. 若PACF在滞后p期截断，ACF拖尾 → 选AR(p)模型；
3. 若两者均拖尾 → 选ARMA(p,q)模型（通过AIC准则进一步优化阶数）。

install.packages("TSA") library(TSA) data(gold) #2005年黄金日价格数据 # 查看数据结构 str(gold)   library(TSA)    # 提供gold数据集 library(tseries) # 用于ACF和Q-Q图 library(forecast)# 辅助时间序列处理 data(gold)  # 加载2005年黄金日价格数据（共252个交易日） # 查看数据基本信息 cat("黄金价格数据维度：", length(gold), "个观测值（2005年交易日）\n") cat("数据时间范围：2005年1月至2005年12月\n")

（a）绘制时间序列图并解释

par(mfrow = c(1, 1), mar = c(4, 4, 2, 1)) plot(gold,      main = "（a）2005年黄金日价格时间序列",      xlab = "交易日（2005年）",      ylab = "价格（美元/盎司）",      col = "blue", lwd = 1.2)

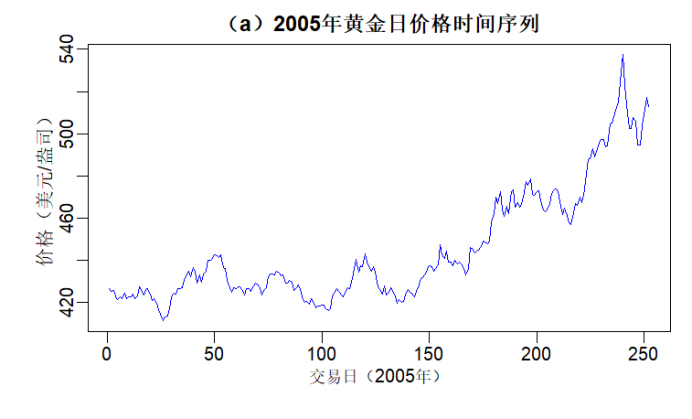
解释：从图中可见，2005年黄金价格整体呈波动上升趋势，年初约420美元，年末接近520美元；价格波动幅度随时间略有增大，存在异方差性，无明显周期性，符合金融时间序列特征。

（b）对数差分及时间序列图

# 对数变换 gold_log <- log(gold) # 对数差分（计算日收益率，近似Δlog(Y_t) = log(Y_t) - log(Y_{t-1})） gold_log_diff <- diff(gold_log) # 转换为时间序列（差分后长度减1，起始时间顺延1个交易日） gold_log_diff_ts <- ts(gold_log_diff, start = start(gold) + c(0, 1), frequency = frequency(gold)) # 绘制对数差分序列图 plot(gold_log_diff_ts,      main = "（b）黄金价格对数差分序列（日收益率）",      xlab = "交易日（2005年）",      ylab = "对数差分收益率",      col = "red", lwd = 1)

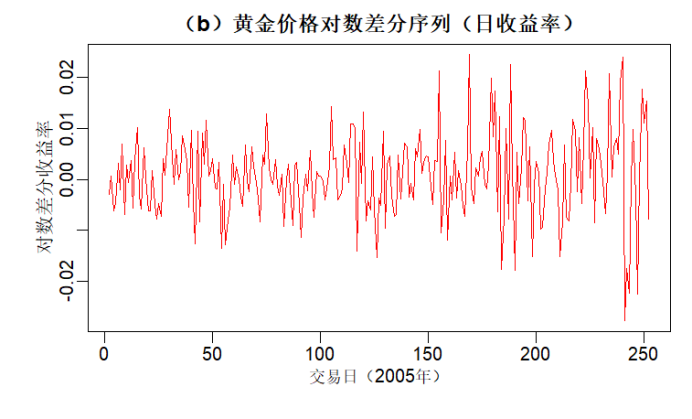
解释：对数差分后序列消除了整体趋势，波动围绕0值上下震荡，更接近平稳序列特征，可以看作黄金价格的日收益率序列。

（c）对数差分序列的ACF及随机游动验证

par(mfrow = c(1, 1)) acf(gold_log_diff,     main = "（c）对数差分序列的样本ACF",     lag.max = 20,  # 最大滞后阶数     col = "darkgreen", lwd = 2)

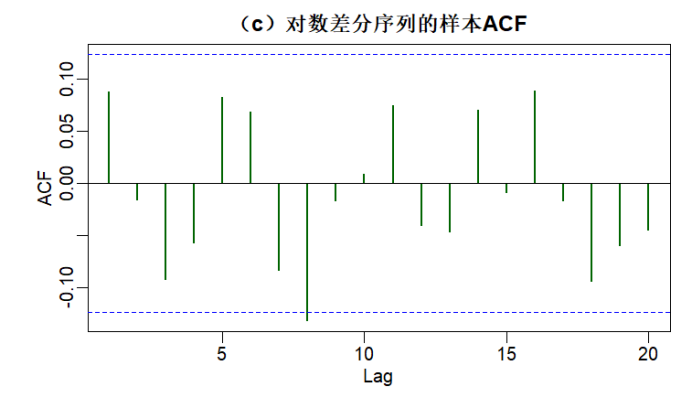
解释：ACF图显示，所有滞后阶数的自相关系数均落在95%置信区间，即蓝色虚线内；无显著自相关性，说明对数差分序列近似为白噪声，可以认为黄金价格的对数服从随机游动模型。

（d）对数差分序列的直方图

# 绘制直方图并叠加正态分布曲线 par(mfrow = c(1, 1)) hist(gold_log_diff,      main = "（d）对数差分序列的直方图",      xlab = "对数差分收益率",      freq = FALSE,  # 显示密度而非频数      col = "lightblue",      border = "white",      breaks = 30)  # 调整 bins 数量 # 叠加正态密度曲线 x <- seq(min(gold_log_diff), max(gold_log_diff), length = 100) lines(x, dnorm(x, mean = mean(gold_log_diff), sd = sd(gold_log_diff)),       col = "red", lwd = 2)

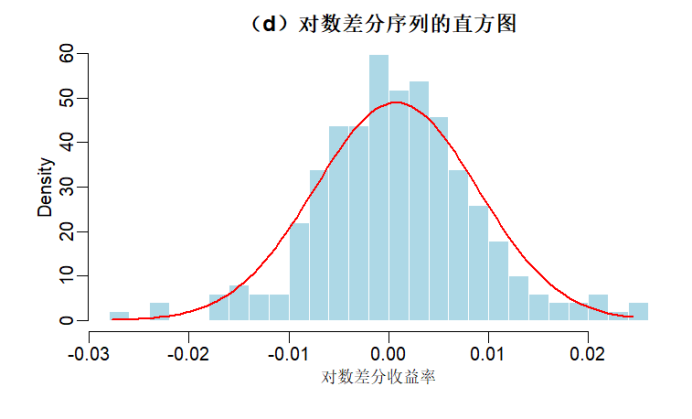
解释：直方图形状与正态分布曲线（红色）大致接近，但尾部略厚，表明日收益率分布近似正态，但可能存在少量极端值。

（e）对数差分序列的正态分位数-分位数图（Q-Q图）

par(mfrow = c(1, 1)) qqnorm(gold_log_diff,        main = "（e）对数差分序列的正态Q-Q图",        col = "purple", pch = 16) qqline(gold_log_diff, col = "black", lwd = 2)  # 添加参考线

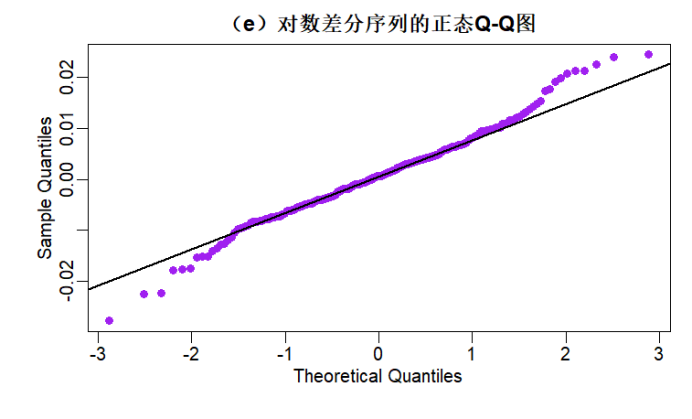
解释：Q-Q图中大部分点近似落在参考线上，但两端尾部略有偏离，进一步验证了“近似正态但非完美正态”的结论，符合金融资产收益率的典型特征。