【算法训练营 · 补充】LeetCode Hot100（上）

二叉树部分

二叉树展开为链表

题目链接：114. 二叉树展开为链表

解题逻辑：

先说原地展开的方法。注意到前序遍历是中左右，我们可以找到当前节点的前驱节点A（左子树的最后一个节点），将当前节点的右孩子接在A的右边，然后将当前节点的左孩子接到右孩子的位置上。依次对链表中的元素进行处理，即可实现。

解题代码：

class Solution {public void flatten(TreeNode root) {      TreeNode cur = root;while(cur != null) {//找到前缀节点if(cur.left != null) {TreeNode preNode = cur.left;while(preNode.right != null) preNode = preNode.right;preNode.right = cur.right;cur.right = cur.left;cur.left = null;}cur = cur.right;}}
}

当然也可以借助队列把中序遍历的元素放到队列中，然后一个个弹出来拼在root的右孩子处：

class Solution {Deque<TreeNode> que = new ArrayDeque<>();public void flatten(TreeNode root) {    preWalk(root);TreeNode pointer = root;if(que.size() == 0 || que.size() == 1) return;que.removeFirst();while(!que.isEmpty()) {pointer.left = null;pointer.right = que.removeFirst();pointer = pointer.right;}}public void preWalk(TreeNode node){if(node == null) return;que.addLast(new TreeNode(node.val));preWalk(node.left);preWalk(node.right);}
}

从前序与中序遍历序列构造二叉树

题目链接：105. 从前序与中序遍历序列构造二叉树

解题思路：

用当前二叉树的前序定根，因为根左右，第一个元素肯定是根，将这个元素带入到中序遍历中，可以确定左右子树的元素。

接下来根据元素个数，通过数组切分得到左子树的前序与中序。重复上述逻辑依次递归，就可以构造出二叉树。

解题代码：

class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {if(preorder.length == 0) return null;if(preorder.length == 1) return new TreeNode(preorder[0]);int num = preorder[0];TreeNode root = new TreeNode(num);int divide = findItem(inorder,num);int[] leftInorder = Arrays.copyOfRange(inorder,0,divide);int[] leftPreorder = Arrays.copyOfRange(preorder,1,1 + leftInorder.length);TreeNode left = buildTree(leftPreorder,leftInorder);int[] rightInorder = null;int[] rightPreorder = null;if(divide == preorder.length - 1) {rightInorder = new int[0];rightPreorder = new int[0];}else {rightInorder = Arrays.copyOfRange(inorder,divide + 1,inorder.length);rightPreorder = Arrays.copyOfRange(preorder,preorder.length - rightInorder.length,preorder.length);}TreeNode right = buildTree(rightPreorder,rightInorder);root.left = left;root.right = right;return root;}public int findItem(int[] nums,int target) {for(int i = 0;i < nums.length;i++) {if(nums[i] == target) return i;}return -1;}
}

注意：

• 因为当数组大小为1或0的时候直接返回，所以左子树的前序与中序是一定存在的
• 但是右子树的前序和中序就不一定了，当divide在中序的尾部时，说明右子树为空，那么此时右子树的前序和中序数组直接返回空数组即可

二叉树的直径

解题逻辑：543. 二叉树的直径

坑点在于最长路径不一定经过根节点。所以需要把每个节点的左最大深度 + 右最大深度比较，取最大的。

这里涉及到两个递归：

• postWalk递归用来获得该节点的最大深度
• search递归遍历树
• 在search中调用postWalk，从递归遍历每个树节点，同时拿到经过该节点的最长路径，遍历完树节点之后取最长的就行。

class Solution {int max = 0;public int diameterOfBinaryTree(TreeNode root) {search(root);return max;}public void search(TreeNode node){if(node == null) return;search(node.left);search(node.right);int path = postWalk(node.left) + postWalk(node.right);if(path > max) max = path;}public int postWalk(TreeNode node){if(node == null) return 0;int left = postWalk(node.left);int right = postWalk(node.right);return Math.max(left,right) + 1;}
}

二叉搜索树中第 K 小的元素

题目链接：230. 二叉搜索树中第 K 小的元素

解题逻辑：

直接用二叉搜索树的特性中序遍历是一个递增序列！

解题代码：

class Solution {List<Integer> list = new ArrayList<>();public int kthSmallest(TreeNode root, int k) {midWalk(root);return list.get(k - 1);}public void midWalk(TreeNode node){if(node == null) return;midWalk(node.left);list.add(node.val);midWalk(node.right);}
}

路径总和 III

题目链接：437. 路径总和 III

解题思路：

可以使用两个递归：

• 一个递归用来获得以当前节点为起点，符合targetSum的路径的条数
• 另一个递归用来遍历整棵树的节点

本题的思想其实和二叉树的直径那一题有点像，不经过跟结点的情况，那么我们可以通过变换参考系来解决。

解题代码：

class Solution {public int pathSum(TreeNode root, int targetSum) {preWalk(root,targetSum);return count;}int count = 0;long curSum = 0;public void searchPath(TreeNode root, int targetSum){if(root == null) return;curSum += root.val;if(curSum == targetSum) count++;searchPath(root.left,targetSum);searchPath(root.right,targetSum);curSum -= root.val;}public void preWalk(TreeNode root,int targetSum){if(root == null) return;searchPath(root,targetSum);preWalk(root.left,targetSum);preWalk(root.right,targetSum);}}

二叉树中的最大路径和

题目链接：124. 二叉树中的最大路径和

解题思想：

通过递归遍历每个节点，同时考虑“穿过该节点的双分支路径”和“从该节点延伸的单分支路径”，从而找到整体最大路径和

解题代码：

class Solution {public int maxPathSum(TreeNode root) {max = root.val;searchPath(root);return max;}int max = 0;public int searchPath(TreeNode root){if(root == null) return 0;int left = searchPath(root.left);int right = searchPath(root.right);int sum = root.val;   int choose = Math.max(left,right);if(choose > 0) sum += choose;if(sum > max) max = sum;int maybe = Math.min(left,right) + sum;if(maybe > max) max = maybe;return sum;}
}

这段代码的核心思路是：

1. 用递归函数 searchPath 计算以当前节点为“起点”，向下延伸（只能选左或右一条分支）的最大路径和（sum），并实时更新全局最大路径和 max。
2. 对于每个节点，除了考虑“单分支路径”（左或右子树选一个），还额外判断了“双分支路径”（左+根+右）的和（maybe），确保不遗漏这种可能的最大路径。
3. 递归返回值是“单分支路径和”（供父节点继续向上拼接），而全局变量 max 则记录所有可能路径中的最大值。

回溯部分

括号生成

题目链接：22. 括号生成

解题思路：

涉及到回溯算法那么能把树状图画出来，就做对了80%：

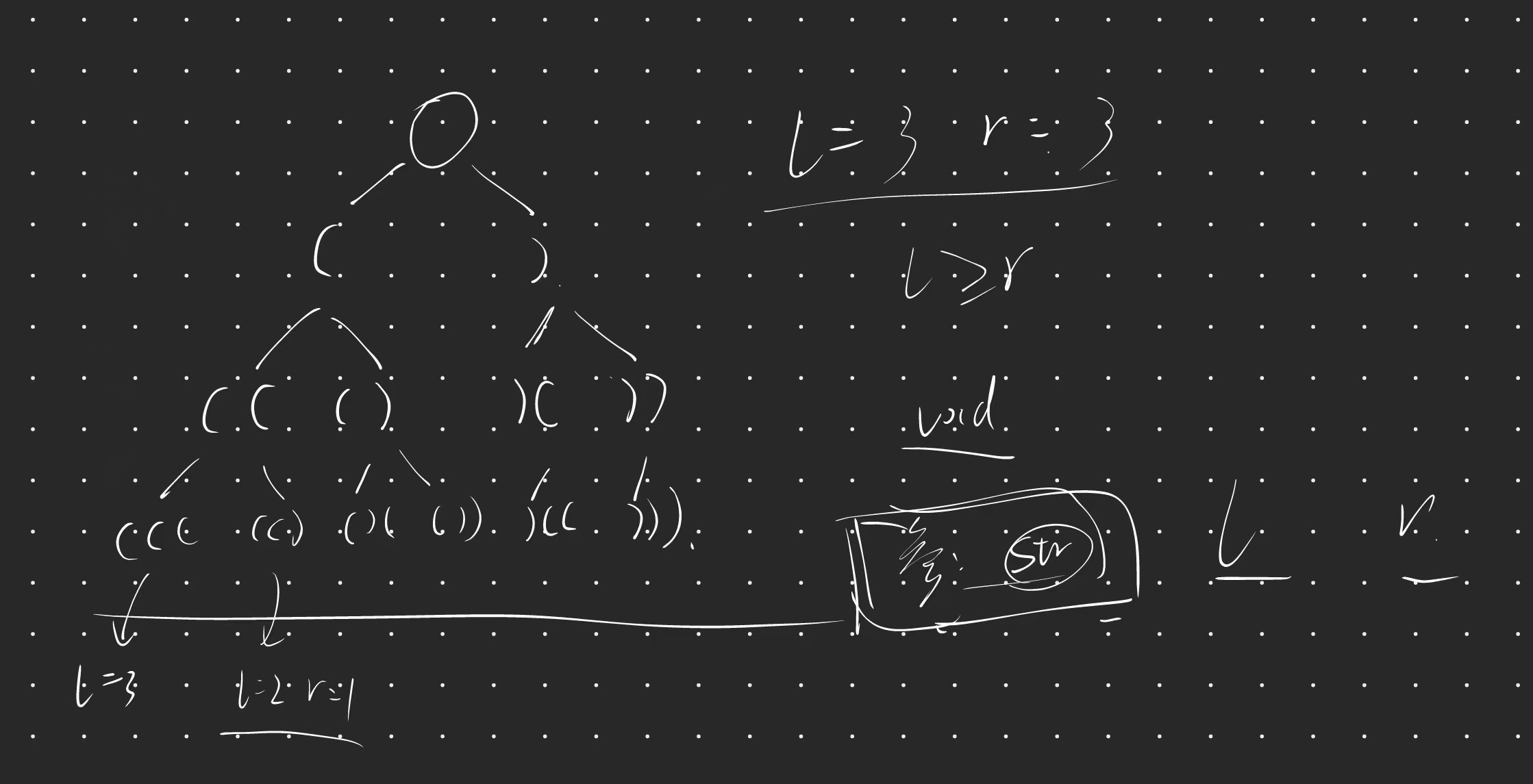
通过递归三部曲来理解：

• 递归参数与返回值：返回值为void，参数需要str记录当前拼接的字符串，left记录左括号个数，right记录右括号个数，n记录需要的对数
• 递归出口：left == n && right == n 说明满足题意进行收集，然后右括号不能大于左括号，括号总数不能超过n的两倍
• 单层逻辑：本层要么拼接左括号要么拼接右括号，递归完成之后要记得回溯把尾部括号去掉

解题代码：

class Solution {public List<String> generateParenthesis(int n) {backtracking("",0,0,n);return result;}List<String> result = new ArrayList<>();public void backtracking(String str,int left,int right,int n){if(left == n && right == n) {result.add(str);return;}if(right > left || str.length() > 2 * n) return;for(int i = 0;i < 2;i++) {if(i == 0) {str += "(";backtracking(str,left + 1,right,n);}else {str += ")";backtracking(str,left,right + 1,n);}str = str.substring(0,str.length() - 1);}}
}

单词搜索

题目链接：79. 单词搜索

解题思路：

遍历board的每个位置，符合开头的则进行递归查找。

本题的注意点在于：

• 需要一个record二维数组记录走过的路径
• 再进行回溯以及遍历查找头遍历节点的时候的时候都要同步更新record数组
• 每一层递归的x，y不要拿着直接用，而是复制一份为x1，y1再用，因为x，y为该层递归的基坐标，是以该点为起点进行上下左右的移动，所以不能随便改变。

解题代码：

class Solution {public boolean exist(char[][] board, String word) {int[][] record = new int[board.length][board[0].length];for(int i = 0;i < board.length;i++) {for(int j = 0;j < board[0].length;j++) {if(board[i][j] != word.charAt(0)) continue;record[i][j] = 1;boolean result = backtracking(board,word,"" + board[i][j],i,j,record);record[i][j] = 0;if(result) return true;}}return false;}int[][] dire = {{1,0},{-1,0},{0,-1},{0,1}};public boolean backtracking(char[][] board, String word,String current,int x,int y,int[][] record){if(current.equals(word)) return true;if(current.length() > word.length()) return false;for(int i = 0;i < 4;i++) {int x1 = x + dire[i][0];int y1 = y + dire[i][1];if(x1 < 0 || x1 >= board.length || y1 < 0 || y1 >= board[0].length || record[x1][y1] == 1) continue;if(board[x1][y1] != word.charAt(current.length())) continue;current += board[x1][y1];record[x1][y1] = 1;boolean result = backtracking(board,word,current,x1,y1,record);if(result) return true;current = current.substring(0,current.length() - 1);record[x1][y1] = 0;}return false;}
}

二分查找部分

与快排的辨析

二分查找和快速排序虽然都运用了分治思想，但它们的核心目标和具体实现方式有显著区别，不能说思想完全一样。

具体来看：

• 二分查找：

  • 用于在有序集合中高效查找目标元素。
  • 核心思路是每次通过与中间元素比较，将查找范围减半（要么在左半部分，要么在右半部分），不断缩小范围直到找到目标或确定不存在。
  • 是查找算法，不改变原集合的结构，时间复杂度为 O(log n)。

• 快速排序：

  • 用于将无序集合排序。
  • 核心思路是选择一个基准元素，将集合分为小于基准和大于基准的两部分（分区操作），然后对这两部分递归排序，最终使整个集合有序。
  • 是排序算法，会改变原集合的顺序，平均时间复杂度为 O(n log n)。

总结来说，两者都通过"分而治之"减少问题规模，但二分查找是单向缩小查找范围，快速排序是双向递归处理分区，应用场景和目标截然不同。

本章二分查找全部使用闭区间处理

搜索插入位置

题目链接：35. 搜索插入位置

解题逻辑：

本题使用二分查找，如果能找到元素直接返回下标，找不到则寻找插入位置，可以转化为查找第一个大于目标的下标，那么其实这个下标就是left所指的地方【可以当作结论记下来】。

为什么？

当指针碰撞之后有三种情况：

• 找到了元素直接返回
• 即使找不到元素，也是在距离该元素最近的相邻位置
  • 如果target小于双指针所指元素，那么left指向的就是第一个大于目标的值
  • 如果target大于双指针所指元素，那么left会右移一个，指向的也是第一个大于目标的值

解题代码：

class Solution {public int searchInsert(int[] nums, int target) {int left = 0;int right = nums.length - 1;  while(right >= left) {int middle = (left + right) / 2;if(nums[middle] == target) return middle;else if(nums[middle] > target) right = middle - 1;else left = middle + 1;}return left;}
}

搜索二维矩阵

题目链接：74. 搜索二维矩阵

解题逻辑：

使用每行的最后一个元素（也就是每行的最大元素），建立一个索引数组，通过二分查找索引数组可以知道应该在matrix的哪一行进行搜索。得到索引之后，我们再去matrix的对应行中再进行二分查找即可。

代码：

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int[] index = new int[matrix.length];for(int i = 0;i < matrix.length;i++) index[i] = matrix[i][matrix[0].length - 1];//二分查找索引int left = 0;int right = index.length - 1;int indexNum = -1;while(left <= right) {int middle = (left + right) / 2;if(index[middle] == target) {indexNum = middle;break;}else if(index[middle] < target) left = middle + 1;else right = middle - 1; }indexNum = indexNum == -1 ? (left == matrix.length ? left - 1 : left) : indexNum;//二分查找具体元素int[] nums = matrix[indexNum];left = 0;right = nums.length - 1;while(left <= right) {int middle = (left + right) / 2;if(nums[middle] == target) return true;else if(nums[middle] < target) left = middle + 1;else right = middle - 1; }return false;}
}

查找元素的第一个和最后一个位置

题目链接：34. 在排序数组中查找元素的第一个和最后一个位置

解题逻辑：

使用二分减小范围的大方向没有变，只是在中间元素为target的时候，两个指针同时向内部逼近，从而得到符合条件的范围。

解题代码：

class Solution {public int[] searchRange(int[] nums, int target) {int left = 0;int right = nums.length - 1;int[] result = {-1,-1};while(left <= right) {int middle = (left + right) / 2;if(nums[middle] == target) {while(nums[left] != target) left++;while(nums[right] != target) right--;result[0] = left;result[1] = right;return result;}else if(nums[middle] < target) left = middle + 1;else right = middle - 1;}return result;}
}

搜索旋转排序数组

题目链接：33. 搜索旋转排序数组

本题就是对应数组在局部有序的情况下二分法怎么用。宗旨不会变：缩小范围，直到找到目标。

解题逻辑：

本题的特点在于：将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环，一步步减少范围.

解题代码：

class Solution {public int search(int[] nums, int target) {int left = 0;int right = nums.length - 1;while(left <= right) {int middle = (left + right) / 2;if(nums[middle] == target) return middle;if(nums[left] <= nums[middle]) {//左边有序if(target >= nums[left] && target < nums[middle]) right = middle - 1;else left = middle + 1;}else {//右边有序if(target > nums[middle] && target <= nums[right]) left = middle + 1;else right = middle - 1;}}return -1;}
}

注意：
nums[left] <= nums[middle]都属于左边有序，即使相等也只能感知到左边，不能判定右边相等。

动态规划部分

杨辉三角

题目链接：118. 杨辉三角

解题逻辑：

从DP四部曲分析：

• dp数组以及下标的含义：dp[i][j]表示对应杨辉三角（i，j）处的值
• 递推公式：dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1]
• 初始化：dp[0][0] = 1
• 遍历顺序：从上到下，从左到右

解题代码：

class Solution {public List<List<Integer>> generate(int numRows) {List<List<Integer>> result = new ArrayList<>();Integer[] arr = {1};result.add(Arrays.asList(arr));Integer[][] dp = new Integer[numRows][numRows];dp[0][0] = 1;for(int i = 1;i < numRows;i++) {for(int j = 0;j <= i;j++) {if(j - 1 < 0 || j > i - 1) dp[i][j] = 1;else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];}result.add(Arrays.asList(Arrays.copyOfRange(dp[i],0,i + 1)));}return result;}
}

乘积最大子数组

题目链接：152. 乘积最大子数组

解题思路：

维护一个二维的dp数组：

• 第一行维护正数最大值
• 第二行维护负数最小值

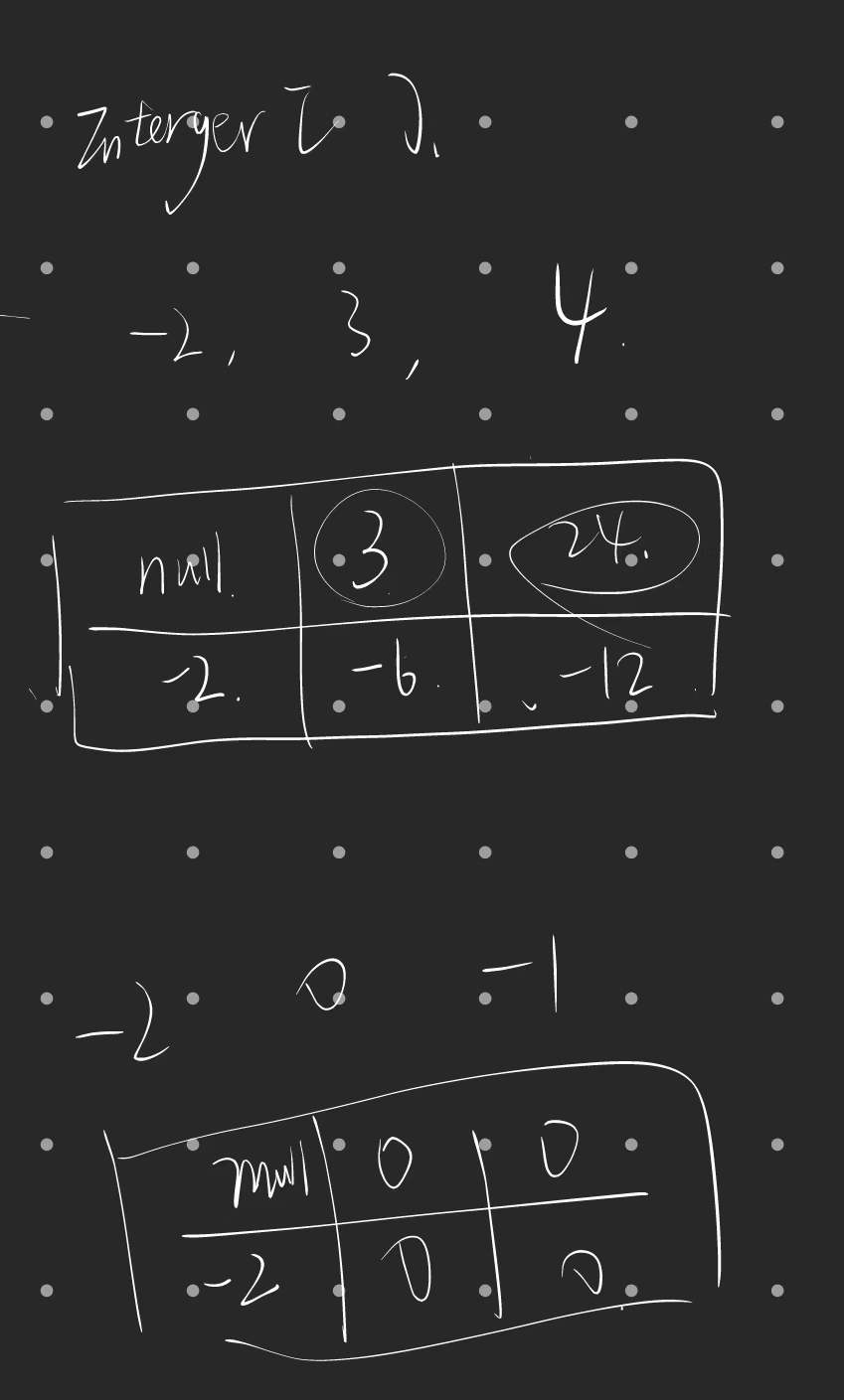
解题代码：

class Solution {public int maxProduct(int[] nums) {Integer[][] dp = new Integer[2][nums.length];dp[0][0] = nums[0] >= 0 ? nums[0] : null;dp[1][0] = nums[0] < 0 ? nums[0] : null;int max = nums[0];for(int j = 1;j < nums.length;j++) {if(nums[j] >= 0) {//当前为正数if(dp[0][j - 1] != null) dp[0][j] = Math.max(nums[j] * dp[0][j - 1],nums[j]);else dp[0][j] = nums[j];if(dp[1][j - 1] != null) dp[1][j] = dp[1][j - 1] * nums[j];}else {//当前为负数if(dp[1][j - 1] != null) dp[0][j] = nums[j] * dp[1][j - 1];if(dp[0][j - 1] != null) dp[1][j] = Math.min(dp[0][j - 1] * nums[j],nums[j]);else dp[1][j] = nums[j];}if(dp[0][j] != null && dp[0][j] > max) max = dp[0][j];     }return max;}
}

最长有效括号

题目链接：32. 最长有效括号

方法1：

使用栈结构，在栈底维护一个边界索引，用于计算有效括号的长度。遇到左括号直接添加。遇到右括号，分为两种情况处理：

• 弹出一个栈顶元素，如果此时栈还没为空，使用当前右括号的索引减去栈顶元素，获得当前有效长度
• 弹出一个栈顶元素，如果此时栈为空（说明此时右括号多了，没有匹配的左括号，所以要重新维护一个边界索引，用于重新计算最长有效括号），把当前右括号入栈重新维护一个边界

解题逻辑：

class Solution {public int longestValidParentheses(String s) {Deque<Integer> stack = new ArrayDeque<>();stack.push(-1);int result = 0;for(int i = 0;i < s.length();i++) {if(s.charAt(i) == '(') stack.push(i);else {int num = stack.pop();if(stack.isEmpty()) {stack.push(i);}else {int cur = i - stack.peek();if(cur > result) result = cur;}}}return result;}
}

最小路径和

题目链接：64. 最小路径和

方法1：回溯算法（时间会超出限制）

class Solution {public int minPathSum(int[][] grid) {backtracking(grid,0,0);return min;}int[][] dire = {{1,0},{0,1}};int min = Integer.MAX_VALUE;int cur = 0;public void backtracking(int[][] grid,int x,int y){if(x >= grid.length || y >= grid[0].length) return;if(x == grid.length - 1 && y == grid[0].length - 1) {cur += grid[x][y];if(cur < min) min = cur;cur -= grid[x][y];return;}for(int i = 0;i < 2;i++) {cur += grid[x][y];int x1 = x + dire[i][0];int y1 = y + dire[i][1];backtracking(grid,x1,y1);cur -= grid[x][y];}}
}

方法2：dp

从DP四部曲分析：

• dp数组以及下标的含义：dp[i][j]表示到达i,j的最小路径和
• 递推公式：dp[i][j] = min(dp[i][j - 1],dp[i - 1][j]) + grid[i][j]
• 初始化：dp[0][0] = 1，第一列以及第一行
• 遍历顺序：从上到下，从左到右

class Solution {public int minPathSum(int[][] grid) {int[][] dp = new int[grid.length][grid[0].length];dp[0][0] = grid[0][0];for(int i = 1;i < grid[0].length;i++) dp[0][i] = dp[0][i - 1] + grid[0][i];for(int i = 1;i < grid.length;i++) dp[i][0] = dp[i - 1][0] + grid[i][0];//dp[i][j] = min(dp[i][j - 1],dp[i - 1][j]) + grid[i][j]for(int i = 1;i < grid.length;i++) {for(int j = 1;j < grid[0].length;j++) {dp[i][j] = Math.min(dp[i][j - 1],dp[i - 1][j]) + grid[i][j];}}return dp[grid.length - 1][grid[0].length - 1];}
}