大规模车辆路径问题的增强神经组合优化(ICRL‘25)

Abstract

神经组合优化（NCO）方法在求解车辆路径问题（VRP）方面已展现出良好性能。然而，大多数NCO方法依赖传统自注意力机制，这会导致过高的计算复杂度，因此难以应对大规模VRP，阻碍了其实际应用。本文提出一种具有线性复杂度的轻量级交叉注意力机制，基于该机制构建Transformer网络，以学习大规模VRP的高效且优质的解决方案。我们还提出**自改进训练（SIT）**算法，该算法可在大规模VRP实例上直接进行模型训练，避免了获取标签时的大量计算开销。通过迭代解重构，Transformer网络自身可生成改进的部分解作为伪标签，以指导模型训练。在节点数高达10万的旅行商问题（TSP）和带容量约束车辆路径问题（CVRP）上的实验结果表明，我们的方法在合成和真实世界基准测试中均持续取得优异性能，显著提升了NCO方法的可扩展性。

代码可在https://github.com/CIAM-Group/SIL获取。

1 Introduction

车辆路径问题（VRP）是一类典型的组合优化问题（COP），在众多实际应用场景中频繁出现（Garaix 等，2010；Brophy & Voigt，2014；Elgarej 等，2021）。由于其NP难的本质，求解VRP仍然极具挑战性（Ausiello 等，2012）。传统方法通常受限于在算法设计中对领域专业知识和调参工作的高度依赖，同时还常因计算效率低下而阻碍其在大规模VRP实例上的适用性。

近年来，以端到端方式求解VRP的神经组合优化（NCO）方法引起了广泛关注（Bengio 等，2021）。这类方法构建深度神经模型，从数据中自动学习问题求解策略，大幅降低了算法设计中高昂的人工投入需求。所学得的策略能够高效生成VRP实例的近似解。在节点数不超过100的小规模问题实例上，尤其是旅行商问题（TSP）和带容量约束车辆路径问题（CVRP）实例上，NCO方法已取得与传统方法相当甚至更优的性能（Kool 等，2019；Kwon 等，2020；Hottung 等，2022）。

然而，现有NCO方法在应用于大规模VRP时往往表现乏力。已有一些研究尝试在节点数最多500的较大规模VRP上训练神经模型（Jin 等，2023；Zhou 等，2023），旨在提升其求解大规模VRP的泛化能力。但随着问题规模的增大，训练难度会急剧上升，导致无法获得足够的泛化能力。因此，部分方法通过分解或学习局部策略来简化大规模VRP（Pan 等，2023；Ye 等，2024；Gao 等，2024；Fang 等，2024）。基于分解的子问题求解器可通过学习构建小规模VRP的完整解或大规模VRP的部分解（例如TSP解的某些片段）来进行训练（Kim 等，2021；Cheng 等，2023；Luo 等，2023）；而基于局部策略的方法则在每个构建步骤中将决策空间缩小至当前节点的邻域内。

尽管在求解大规模车辆路径问题（VRP）方面已做出上述努力，但当前神经组合优化（NCO）方法在可扩展性上仍面临两大障碍。首先，这些方法通常依赖计算复杂度较高的传统自注意力机制（Vaswani 等，2017），这严重限制了模型为大规模 VRP 构建完整解或多个大规模部分解的效率。其次，它们的模型常以监督学习（SL）或强化学习（RL）的方式进行训练，而这两种方式在大规模 VRP 的有效训练中均存在困难。一方面，基于监督学习的 NCO 难以获取足够多的（近）最优解作为标签；另一方面，基于强化学习的模型训练面临严重的奖励稀疏问题，且 GPU 内存占用量较高。

本文提出一种具有线性计算复杂度的轻量级交叉注意力机制，该机制可显著提升 NCO 模型求解大规模 VRP 的效率。与传统自注意力机制要求实例中每个节点都关注所有其他节点不同，交叉注意力机制通过代表性节点重构计算过程。具体而言，代表性节点先关注实例中的每个节点以更新自身嵌入，随后实例中所有节点再通过关注代表性节点来更新自身嵌入。由于代表性节点数量固定，与传统自注意力机制相比，该机制在大幅降低计算复杂度的同时，仍能保证节点间有效的注意力计算。
基于所提出的交叉注意力机制，我们构建了一种新型 Transformer 网络，以更高效地求解大规模 VRP。此外，我们还提出一种创新性的自改进训练（SIT）算法，使模型能在大规模实例上成功训练。该算法利用 Transformer 网络自身，通过迭代重构优化解；而优化后的解反过来作为伪标签，用于训练网络。通过迭代执行解重构与网络训练，SIT 算法使我们的 NCO 方法无需任何带标签数据，就能有效求解大规模 VRP 实例。

我们在合成与真实世界的旅行商问题（TSP）和带容量约束车辆路径问题（CVRP）基准测试集上开展了全面实验。结果表明，我们的 NCO 方法在节点数高达 10 万个的大规模 VRP 上实现了当前最优性能。我们的消融实验揭示了交叉注意力机制与 SIT 算法在提升大规模 VRP 计算效率和求解性能方面的作用

2 相关工作

2.1 基于泛化的方法

基于泛化的方法通常在小规模实例上训练神经模型，随后在相同规模或更大规模的实例上对其进行测试。它一般指的是基于构造的方法，这类方法会学习一个模型，以自回归的方式为给定的问题实例构造近似解。先驱性研究（Vinyals 等，2015；Bello 等，2016；Nazari 等，2018）表明，通过监督学习（SL）或强化学习（RL）训练的神经模型，在小规模组合优化（CO）问题上能够取得良好的效果。Kool 等（2019）和 Deudon 等（2018）利用 Transformer 结构（Vaswani 等，2017）开发了强大的基于注意力的模型，用于求解小规模车辆路径问题（VRP）。此后，多种带有不同改进的基于 Transformer 的方法被相继提出（Xin 等，2021a；2020；Kwon 等，2020；Hottung 等，2022；Kim 等，2021；Choo 等，2022；Manchanda 等，2022）。

随后，许多研究尝试提升神经模型在大规模车辆路径问题上的性能（Son 等，2023；Zhou 等，2023；Drakulic 等，2023；Luo 等，2023）。其中，Drakulic 等（2023）、Luo 等（2023）采用监督学习在 100 节点实例上训练模型，使模型在节点数最多 1000 的车辆路径问题上具备良好的泛化能力。BQ 重新构建了解构造的马尔可夫决策过程（MDP），以有效利用组合优化问题的常见对称性；而 LEHD 提出轻编码器 - 重解码器结构来实现相同目标。然而，由于 100 节点实例的分布与 10000 节点以上实例的分布差异极大，从小规模实例中学习到的特征无法适用于超大规模实例，从而导致在 10000 节点以上的实例上性能表现不佳。近期的尝试提出在节点数最多 500 的更大规模实例上训练模型（Jin 等，2023；Zhou 等，2024；Wang 等，2024；Zhou 等，2023）。但随着问题规模的增大，训练难度急剧上升，进而导致无法获得足够的泛化能力。

2.2 基于简化的方法

部分方法通过分解或学习局部策略来简化大规模车辆路径问题（VRP）。一方面，基于分解的方法通常将大规模问题转化为多个更简单的小规模子问题，求解这些子问题后，再合并其解以构造原大规模问题的完整解。这类方法提出不同策略，分别学习用于问题分解和子问题求解的独立模型（Li 等，2021；Zong 等，2022；Hou 等，2023；Pan 等，2023；Ye 等，2024）。基于分解的子问题求解器可通过学习构造小规模 VRP 的完整解或大规模 VRP 的部分解（例如旅行商问题（TSP）解的某些片段）来进行训练（Kim 等，2021；Cheng 等，2023；Luo 等，2023）。
另一方面，基于局部策略的方法在每个构造步骤中将决策空间缩小至当前节点的邻域内。Gao 等（2024）采用辅助策略引导模型在当前节点邻域内做决策，而 Fang 等（2024）则直接将决策限制在邻域内。

2.3 基于热图的方法

除上述研究外，已有学者提出一些基于热图的方法来解决大规模旅行商问题（TSP）实例（Fu 等，2021；Qiu 等，2022；Li 等，2023；Min 等，2023；Sun & Yang，2023）。这类方法首先构建一个图神经网络（GNN）模型，预测一个热图——该热图用于衡量每条边出现在最优解中的概率，随后利用该热图迭代搜索近似解（Joshi 等，2019）。

由于这类方法依赖专为TSP设计的搜索策略（例如蒙特卡洛树搜索（MCTS）（Fu 等，2021）），因此无法应用于求解带容量约束车辆路径问题（CVRP）等其他复杂组合优化（CO）问题。本文中，我们主要关注无需专家知识的基于构造的方法。

3 预备知识

车辆路径问题（VRP）定义：一个VRP实例$S$可由图$\mathcal{G}=(\mathcal{V},\mathcal{E})$表示，其中节点集V={vi}i=0n\mathcal{V} = \{v_i\}_{i=0}^nV={vi​}i=0n​，边集$\mathcal{E}=\{(v_i,v_j)|v_i,v_j\in \mathcal{V},v_i\ne v_j\}$。特别地，在部分问题（如带容量约束车辆路径问题（CVRP））中，$v_0$表示配送中心（depot）。

在VRP图中，每个节点由向量${\mathbf{x}}_i\in {\mathbb{R}}^{d_x}$刻画，其元素包含节点坐标及其他问题特定属性（例如，CVRP中的需求{δi}i=0n\{\delta_i\}_{i=0}^n{δi​}i=0n​）。VRP实例的解是一条回路$\pi$，即节点的一个排列。给定成本函数$c(\cdot )$，求解VRP实例需从可行回路集合$\Omega$中寻找成本最小的回路，即${\pi }^{\ast }=\arg {\min }_{\pi \in \Omega }c(\pi |\mathcal{G})$。本文中，旅行商问题（TSP）和CVRP的成本函数定义为回路的欧几里得长度。

若VRP解满足问题特定约束，则该解是可行的。例如，TSP实例的可行解是一条恰好访问图中每个节点一次的回路；CVRP的约束还进一步涉及车辆的容量限制，其细节见附录B。

车辆路径问题（VRP）的解构造 大多数神经组合优化（NCO）方法采用基于编码器-解码器的神经网络来学习解的构造过程。编码器为每个节点$v_i$生成节点嵌入${\mathbf{h}}_i$。借助节点嵌入{hi}i=0n\{\mathbf{h}_i\}_{i=0}^n{hi​}i=0n​，解码器通过在每一步将一个节点添加到部分解中，来顺序构造完整解。

特别地，若所有节点均未被访问过，部分解为空。在每个构造步骤中，从未访问节点中选择一个节点添加到部分解中，并标记为已访问。例如，步骤$t$时的部分解可表示为$({\pi }_1,{\pi }_2,\dots ,{\pi }_{t-1})$，其中${\pi }_1,{\pi }_{t-1}\in \mathcal{V}$分别是第一个和最后一个被访问的节点。该过程持续进行，直到所有节点都被访问，最终返回完整解。

（自）注意力机制

给定嵌入矩阵$X\in {\mathbb{R}}^{n\times d}$和$C\in {\mathbb{R}}^{m\times d}$（其中$d$为嵌入的维度），缩放点积注意力可公式化为：

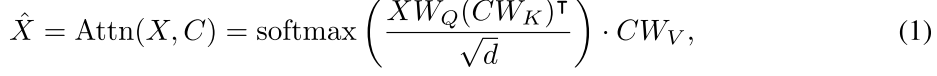
其中$W_Q,W_K,W_V\in {\mathbb{R}}^{d\times d}$ 是可学习矩阵。注意力$\text{Attn}(\cdot ,\cdot )$可将$C$的信息聚合到$X$中。常用的多头注意力（MHA）进一步并行执行$h$次注意力计算。为简洁起见，本文通篇省略$h$。

通常，传统Transformer架构的主要复杂度源于计算式(1)中的注意力，其计算和内存复杂度为$\mathcal{O}(nm)$。尤其当嵌入矩阵相同时（即$X=C$），式(1)定义的自注意力复杂度为$\mathcal{O}(n^2)$。

4 方法

在本节中，我们首先介绍为求解车辆路径问题（VRP）量身定制的交叉注意力机制。随后，我们介绍基于交叉注意力的Transformer网络和SIT算法。为不失一般性，我们以旅行商问题（TSP）为例阐述我们的方法。带容量约束车辆路径问题（CVRP）的实现细节见附录B。

4.1 面向VRP的轻量级交叉注意力

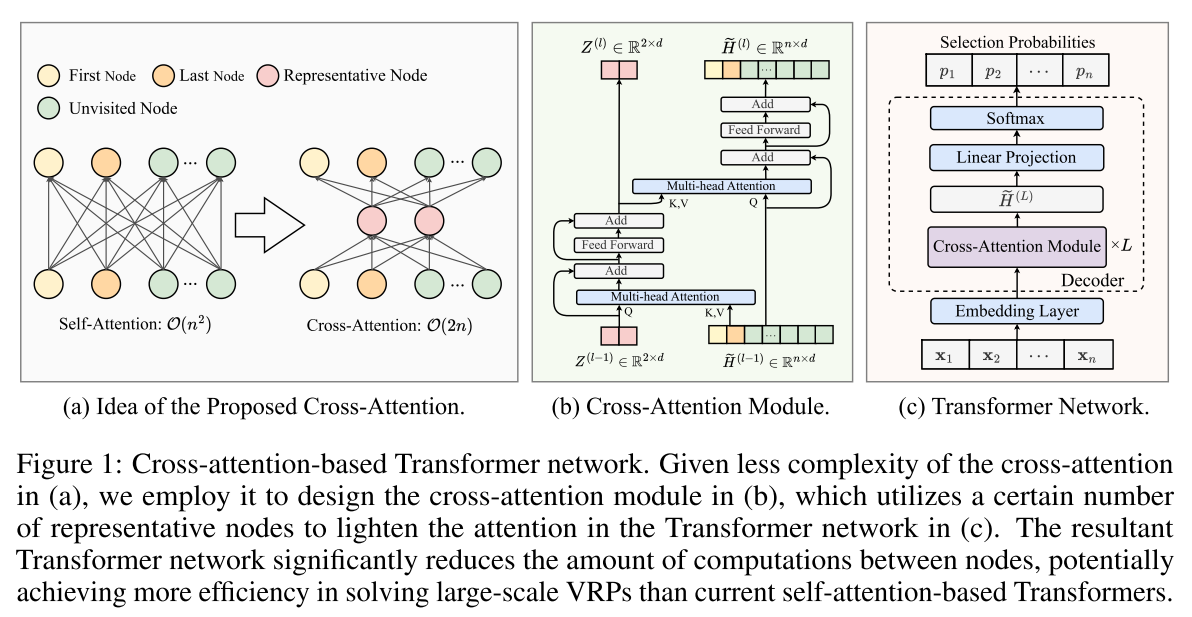
如图1(a)所示，自注意力（堆叠在编码器或解码器中）要求每个输入节点与VRP实例的所有其他节点进行全面交互，以更新其嵌入（Kwon 等，2020；Pirnay & Grimm，2024；Luo 等，2023）。然而，这不可避免地导致$\mathcal{O}(n^2)$的计算和内存复杂度，其中$n$是实例中的节点数，即问题规模。随着规模增大，这些复杂度急剧上升，使得模型难以在大规模VRP实例上训练。我们在代表性神经组合优化（NCO）方法上的实证结果验证了其二次复杂度，如实验中的表4所示。

为解决这一问题，我们设计了一种轻量级交叉注意力机制，可显著降低计算和内存复杂度。如图1(a)所示，我们在注意力计算中使用两个代表性节点。这两个代表性节点首先基于它们与实例所有节点之间的注意力来更新自身嵌入。随后，通过对代表性节点进行注意力计算，更新实例的节点嵌入。与自注意力相比，该交叉注意力的复杂度为$\mathcal{O}(nm)$（其中$m$是代表性节点的数量）。由于通过代表性节点传播节点嵌入，交叉注意力机制在实现低复杂度的同时，保持了节点间的有效交互。

4.2 Transformer网络

我们遵循重解码器范式（Drakulic 等，2023；Luo 等，2023），开发了一种基于交叉注意力的Transformer网络，用于求解大规模车辆路径问题（VRP）。如图1 ( c )所示，该网络由一个嵌入层和一个包含$L$个堆叠交叉注意力模块的解码器组成，下文将对其进行详细说明。

嵌入层：给定一个含$n$个节点的VRP实例( S )，嵌入层通过线性投影将节点特征{xi}i=1n∈Rn×dx\{\mathbf{x}_i\}_{i=1}^n \in \mathbb{R}^{n \times d_x}{xi​}i=1n​∈Rn×dx​转换为初始节点嵌入{hi}i=1n∈Rn×d\{\mathbf{h}_i\}_{i=1}^n \in \mathbb{R}^{n \times d}{hi​}i=1n​∈Rn×d，即${\mathbf{h}}_i=W^{(0)}{\mathbf{x}}_i+{\mathbf{b}}^{(0)}$，∀i∈{1,…,n}\forall i \in \{1, \dots, n\}∀i∈{1,…,n}，其中$W^{(0)}\in {\mathbb{R}}^{d_x\times d}$和${\mathbf{b}}^{(0)}\in {\mathbb{R}}^d$是可学习的。

含交叉注意力模块的解码器：在第$t$个解码步骤，我们从当前部分解$({\pi }_1,\dots ,{\pi }_{t-1})$中选择第一个和最后一个节点${\pi }_1$, ${\pi }_{t-1}$作为代表性节点。这些代表性节点反映了解构造过程中的动态变化，在文献中常被用作上下文节点（Kwon 等，2020；Luo 等，2023；Kool 等，2019）。我们还探索了代表性节点的其他配置，并评估其对性能的影响。更多细节见附录C。

给定代表性节点，我们设计交叉注意力模块以更新节点嵌入，如图1(b)所示。在第t个解码步骤中，第一个和最后一个节点的嵌入分别记为${\mathbf{h}}_{{\pi }_1}$和${\mathbf{h}}_{{\pi }_{t-1}}$。未访问节点的嵌入记为Hat={hi∣i∈{1,…,n}∖{π1:t−1}}H_a^t = \{\mathbf{h}_i \mid i \in \{1, \dots, n\} \setminus \{\pi_{1:t-1}\}\}Hat​={hi​∣i∈{1,…,n}∖{π1:t−1​}}。在第一个解码步骤中，随机选择一个节点${\pi }_1$作为部分解，并将其视为下一次解码的第一个和最后一个节点。所有其他节点保持未访问状态，即Ha0={hi∣i∈{1,…,n}∖π1}H_a^0 = \{\mathbf{h}_i \mid i \in \{1, \dots, n\} \setminus \pi_1\}Ha0​={hi​∣i∈{1,…,n}∖π1​}。相应地，我们在第$t$个解码步骤中定义初始代表性节点嵌入$Z^{(0)}$和图节点嵌入${\tilde{H}}^{(0)}$如下：

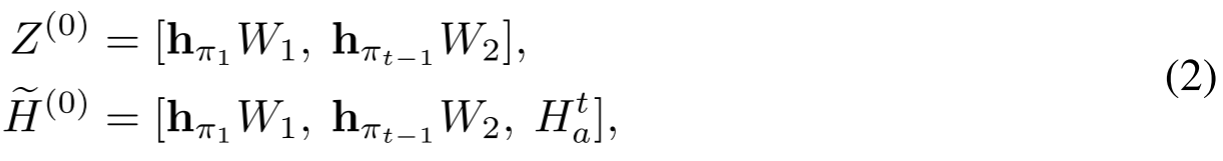
其中$[\cdot ,\cdot ]$表示垂直拼接操作符，$W_1,W_2\in {\mathbb{R}}^{d\times d}$是可学习矩阵。

接下来，$Z^{(0)}\in {\mathbb{R}}^{2\times d}$和${\tilde{H}}^{(0)}\in {\mathbb{R}}^{N\times d}$由$L$个交叉注意力模块处理。在第$l$个交叉注意力模块中，我们首先让代表性节点关注图节点嵌入${\tilde{H}}^{(l-1)}$，以更新代表性节点嵌入，即：

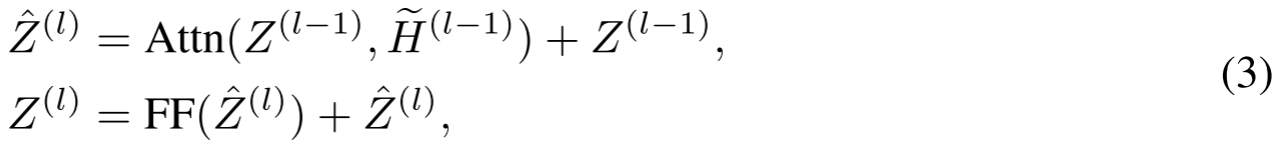
其中FF表示前馈层，其公式为$\text{FF}(X)=\max (0,X{W}_{f1}+{\mathbf{b}}_{f1})W_{f2}+{\mathbf{b}}_{f2}$，其中$W_{f1}\in {\mathbb{R}}^{d\times d_f}$、${\mathbf{b}}_{f1}\in {\mathbb{R}}^{d_f}$、$W_{f2}\in {\mathbb{R}}^{d_f\times d}$、${\mathbf{b}}_{f2}\in {\mathbb{R}}^d$是可学习矩阵，$d_f$是该层的隐藏维度。

随后，图节点嵌入${\tilde{H}}^{(l-1)}$关注代表性节点，以更新自身嵌入，即：

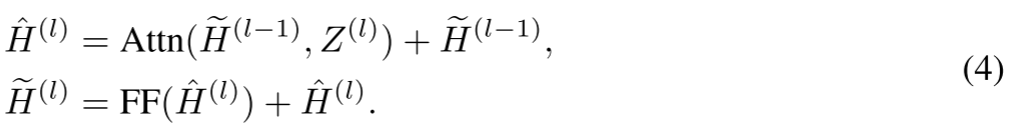
经过$L$个交叉注意力模块后，输出${\tilde{H}}^{(L)}$包含第一个节点、最后一个节点和未访问节点的更新后嵌入。对未访问节点的嵌入{h~i(L)∣i∈{1,…,n}∖{π1:t−1}}\{\widetilde{\mathbf{h}}_i^{(L)} | i \in \{1, \dots, n\} \setminus \{\pi_{1:t-1}\}\}{hi(L)​∣i∈{1,…,n}∖{π1:t−1​}}应用线性投影和softmax函数，以生成选择每个未访问节点的概率，即：

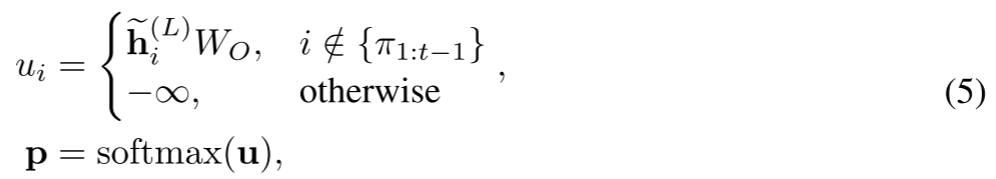
其中$W_O\in {\mathbb{R}}^{d\times 1}$是可学习矩阵。每个$p_i\in \mathbf{p}$对应选择未访问节点$i$的概率。我们根据这些概率对节点进行采样，并将其添加到部分解中。经过$n$个解码步骤，构建出完整的VRP解$\pi =({\pi }_1,\dots ,{\pi }_n)$。

复杂度分析

根据式(3)，交叉注意力模块的输入维度中，$Z^{(l-1)}$ 为${\mathbb{R}}^{2\times d}$，${\tilde{H}}^{(l-1)}$ 为${\mathbb{R}}^{\tilde{n}\times d}$，其中$\tilde{n}\le (n+1)$是输入到解码器的节点嵌入数量。

除常数$d$（在大多数神经组合优化（NCO）方法的Transformer中$d=128$）外，节点嵌入$Z^{(l-1)}$与${\tilde{H}}^{(l-1)}$之间的交叉注意力复杂度为$\mathcal{O}(2\tilde{n})$。类似地，式(4)呈现相同的线性复杂度。

通过设置固定数量的代表性节点，交叉注意力显著减少了所有节点间的计算量，比NCO方法中主流的基于自注意力的Transformer更轻量。

4.3 自改进训练

基于构造的神经组合优化（NCO）模型在解码时存在偏差，起始节点、目标节点和方向的差异会导致截然不同的解（Kwon 等，2020）。借助这种偏差，模型可通过执行迭代局部重构直至收敛，逐步提升解的质量（Luo 等，2023；Ye 等，2024）。这种范式在无需探索完整解的情况下，具备高效发现更优解的巨大潜力。

然而，当前的局部重构技术仍依赖监督学习（SL）或强化学习（RL），由于标签稀缺或奖励稀疏，这阻碍了它们在大规模车辆路径问题（VRP）上的适用性。对此，我们提出 自改进训练（SIT） 算法，专注于局部重构，以更有效地在大规模VRP上探索解。如图2所示，SIT包含迭代局部重构和模型训练，下文将对其详细阐述。

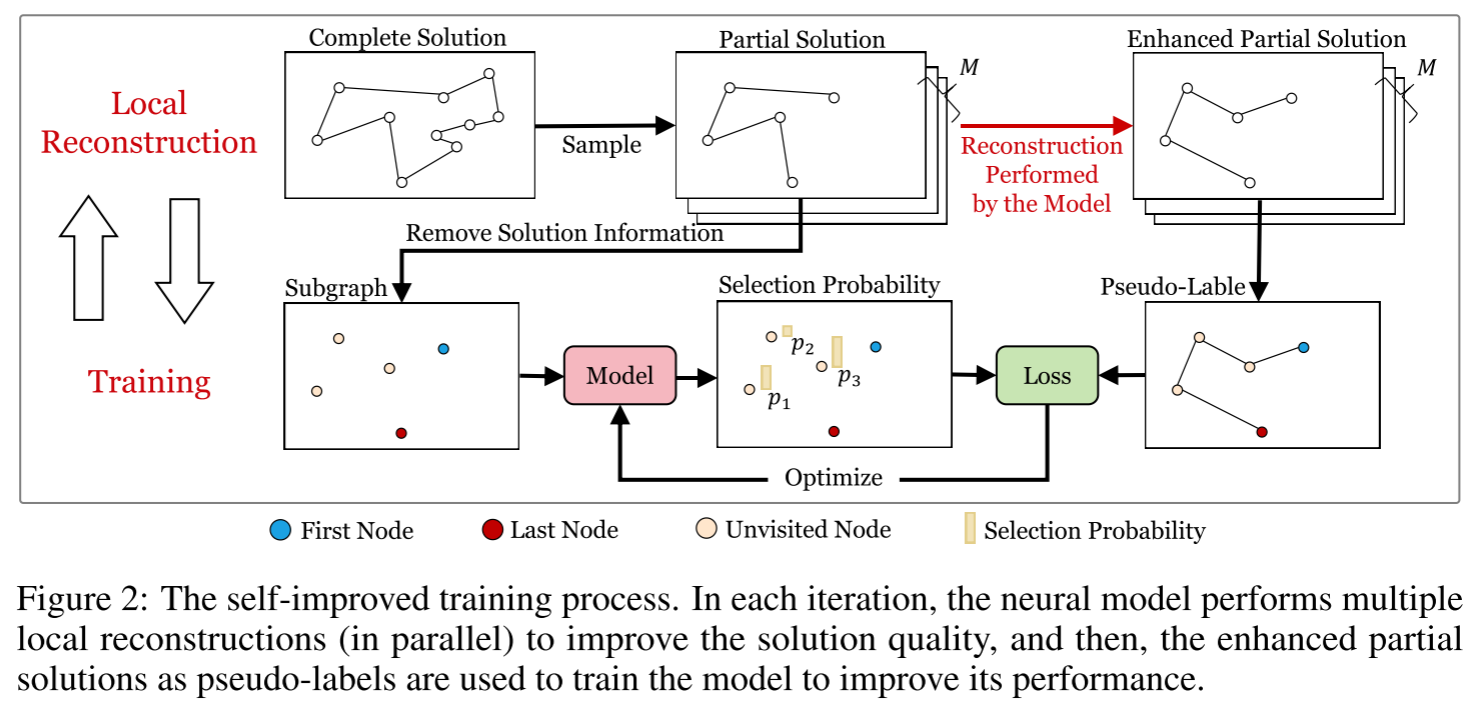
局部重构

局部重构包含两个步骤。第一步，从解 $\pi$ 中采样一个规模随机（满足$4\le \omega \le l_{max}$）的部分解${\pi }^p$，其中$l_{max}$为部分解的最大规模。由于$\pi$可表示为节点构成的环路，我们允许采用顺时针或逆时针方向进行采样。第二步，神经模型从该部分解的第一个节点到最后一个节点逐个重构节点，即重新排列第一个节点与最后一个节点之间的节点顺序。将生成的部分解${\pi }^{p\prime }$与${\pi }^p$进行比较，在完整解$\pi$中采用更优的那个（例如，长度更短的）。换句话说，更优的部分解可带来更优的完整解。通过迭代局部重构，解$\pi$的质量可显著提升。

为提高重构效率，我们采样$M$个不重叠的部分解并并行进行重构。通过将解均匀划分为$M$个长度为$\omega$的连续片段来避免重叠，在这些片段中可并行执行采样和重构操作。本文中，我们将$M$设为$\lfloor n/\omega \rfloor$（其中$n$表示问题规模）。在整个SIT过程中，我们维护一个数据集$\mathcal{D}$，其中包含通过局部重构更新的VRP实例及其解。在每次SIT迭代中，局部重构会逐步提升数据集中解的质量，避免重复访问之前探索过的解，从而提高效率。

模型训练

局部重构得到的增强解作为伪标签，以监督学习的方式训练模型。对于大规模VRP实例（例如含10万个节点的TSP实例），由于GPU内存占用极大，学习构造其完整解会面临困难。为缓解这一问题，我们将模型的学习范围限制在解的局部部分。具体而言，采用规模随机$(4\le \omega \le l_{max}$）的方式从数据集$\mathcal{D}$中采样部分解。设${\hat{\pi }}_{1:\omega }^p=({\hat{\pi }}_1^p,{\hat{\pi }}_2^p,\dots ,{\hat{\pi }}_{\omega }^p)$为采样得到的部分解，将其作为伪标签，模型通过参数为$\theta$的所提Transformer网络学习预测从${\hat{\pi }}_1^p$到${\hat{\pi }}_{\omega }^p$的顺序。损失函数可公式化为：

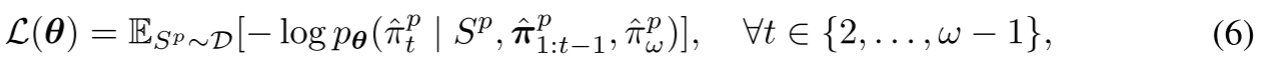
其中${\hat{\pi }}_1^p$和${\hat{\pi }}_{\omega }^p$分别表示部分解的第一个和最后一个节点，它们的嵌入构成式(2)中的代表性节点嵌入和图节点嵌入。${\hat{\pi }}_{1:t-1}^p$表示第$t$个解码步骤前已访问节点的序列。通过部分解训练，模型在局部重构过程中能更高效地提升解的质量。

SIT过程在局部重构和模型训练之间交替进行，直到达到预定义的时间预算。详细的训练过程和伪代码见附录D。

5 实验

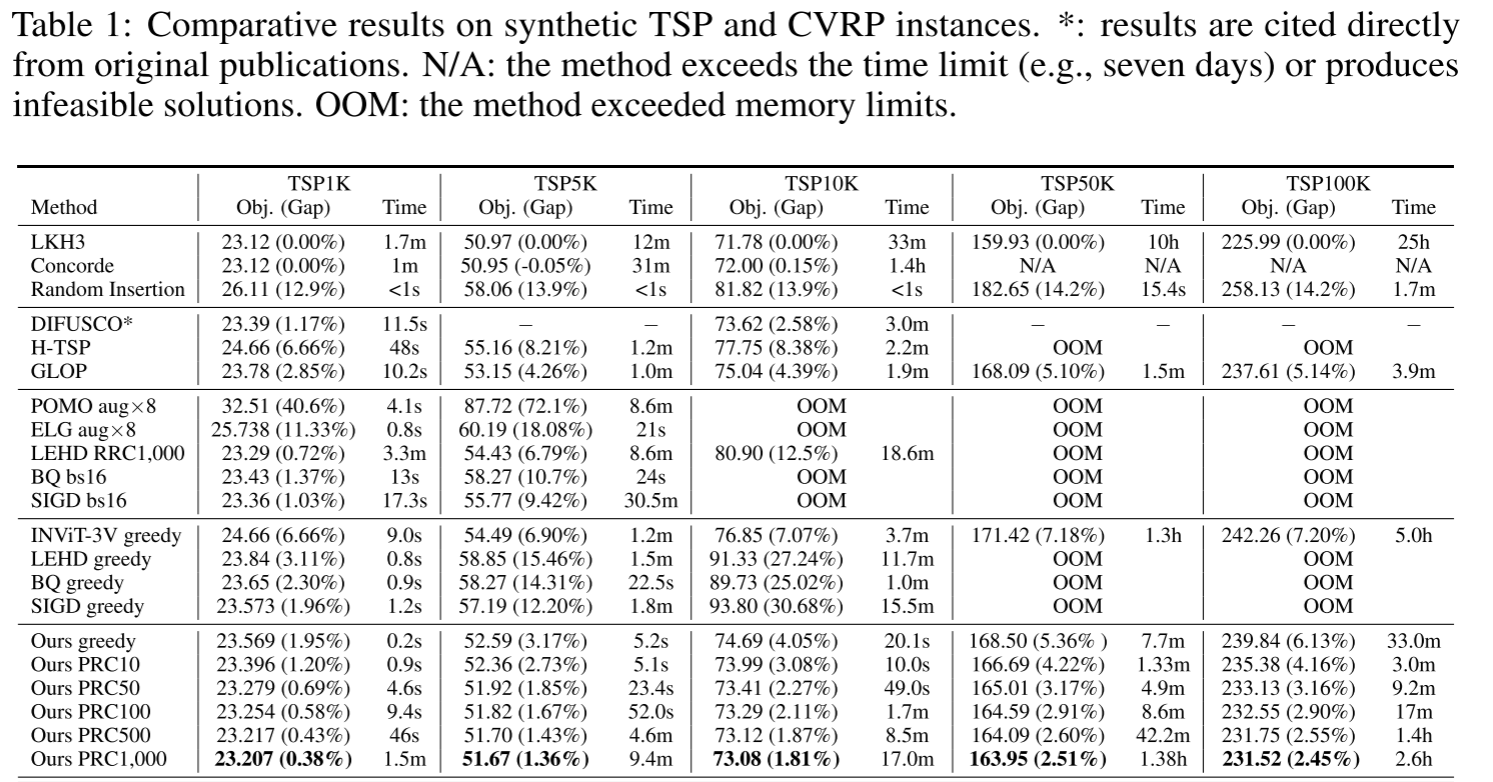
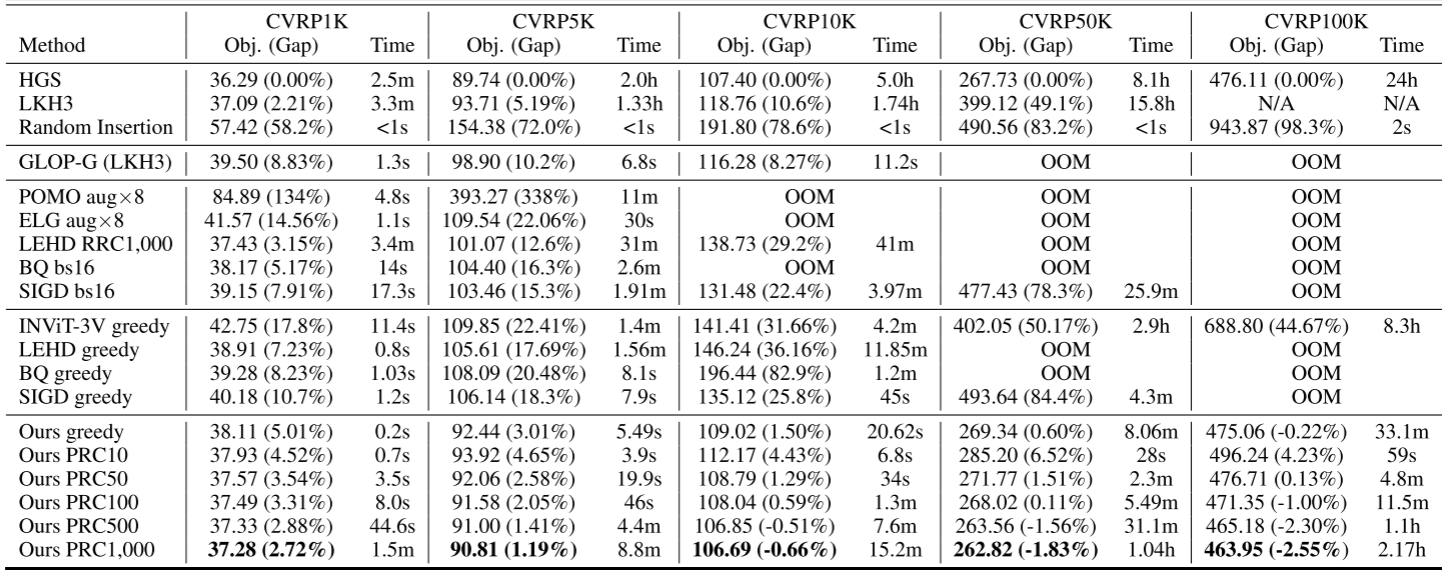
我们从两个角度对所提方法进行实证评估。首先，将所提方法与多种基准方法进行比较，以验证其在合成和真实世界大规模旅行商问题（TSP）和带容量约束车辆路径问题（CVRP）实例上的性能。随后，分析所提方法关键组件的影响，以验证我们的方法在降低计算和内存复杂度方面的能力，并分析关键超参数。

数据集：遵循文献中的常见方法（Kool 等，2019；Kwon 等，2020；Luo 等，2023），我们生成五个合成数据集，分别包含规模为1K、5K、10K、50K和100K的实例。我们将这些规模的TSP和CVRP实例分别记为TSP/CVRP1K、5K、10K、50K和100K。根据（Fu 等，2021），我们将TSP1K测试数据集的实例数量设为128。对于包含更大实例的数据集，每个数据集包含16个实例。类似地，CVRP测试数据集包含相同数量的实例，CVRP1K的容量设为250，CVRP5K为500，CVRP10K为1000，CVRP50K/100K为2000。TSP实例的最优解使用LKH3（Helsgaun，2017）计算，而CVRP实例通过HGS（Vidal，2022）求解。为了在真实世界大规模实例上评估我们的方法，我们还从TSPLIB（Reinelt，1991）和CVRPLIB（Uchoa 等，2017）中提取所有具有EUC_2D特征且节点数超过1K的对称实例，共33个TSP实例和14个CVRP实例。

模型设置与训练

对于我们的Transformer网络，设置嵌入维度( d = 128 )。解码器采用( L = 6 )个堆叠的交叉注意力模块，每个注意力层包含8个注意力头，且有一个隐藏维度为512的前馈层。模型最初使用随机插入生成的伪标签，在1K规模的实例上进行预热训练（详见附录D）。之后，在1K规模的实例上继续自改进训练，再利用训练好的模型在更大规模（包括5K、10K、50K和100K）的实例上分别开展训练。

1K、5K/10K、50K/100K规模对应的训练数据集大小( D )分别为20K、200和100。我们的SIT算法中，每次迭代包含100次局部重构和20个epoch的模型训练。采用Adam优化器（Kingma & Ba，2015）训练模型，初始学习率为1e-4，每个epoch的衰减率为0.97。在整个SIT过程中，部分解的最大长度( l_{max} )设为1000，以平衡效率和有效性。在所有实验中，我们使用单块NVIDIA GeForce RTX 3090 GPU（24GB内存）进行训练和测试。更多详细的训练设置见附录E。

基准方法

我们将所提方法与以下类别基准方法进行比较：
1）经典求解器：Concorde（Applegate等，2006）、LKH3（Helsgaun，2017）和HGS（Vidal，2022）；
2）插入启发式算法：随机插入；
3）基于构造的NCO方法：POMO（Kwon等，2020）、BQ（Drakulic等，2023）、LEHD（Luo等，2023）、INViT（Fang等，2024）和SIGD（Pirnay & Grimm，2024）；
4）基于热图的方法：DIFUSCO（Sun & Yang，2023）；
5）基于分解的方法：GLOP（Ye等，2024）和H-TSP（Pan等，2023）；
6）基于局部策略的方法：ELG（Gao等，2024）。

6 结论

在本文中，我们提出了一种具有线性复杂度的轻量级交叉注意力机制，以提升神经组合优化（NCO）模型求解大规模车辆路径问题（VRP）的效率。得益于通过代表性节点传播节点嵌入，该交叉注意力机制在实现低复杂度的同时，保持了节点间的有效交互。此外，我们开发了一种新颖的Transformer网络来学习高效且优质的解，其中交叉注意力被迭代用于更新节点嵌入。

此外，我们提出了一种创新性的自改进训练（SIT）算法，可在无需标签数据的情况下直接在大规模VRP实例上训练模型。在合成和真实世界分布中，针对节点数最多达10万的旅行商问题（TSP）和带容量约束车辆路径问题（CVRP）的大量实验结果，充分证明了我们方法的优越性能。

由于在采样部分解时预定义了特定的随机规模范围，一个潜在的改进方向是开发一种自适应策略来设置部分解的采样规模，从而实现更高效的模型训练和PRC。此外，我们将把我们的方法扩展到其他类型的组合优化问题，如调度、装箱和背包问题。