大模型应用开发面经

1.介绍一下Transformers是什么，原理及应用以及其目前最大创新？

Transformer 是一种神经网络架构，“Attention is All You Need”。

最核心的思想是用 自注意力（self-attention）机制 来建模序列中任意位置之间的依赖关系，从而替代之前主流的 RNN/LSTM（顺序处理）和大多数卷积方法。

Transformer 的出现使得模型可以高度并行训练、有效捕捉长程依赖，并成为现代大规模预训练-微调（pretrain → fine-tune）范式的基础，推动了 BERT、GPT、T5、ViT 等一大批里程碑模型的诞生。

核心原理：

1.自注意力（self-attention）

自注意力是 Transformer 的核心单元，通过三个线性变换得到查询Q，键K和值V：

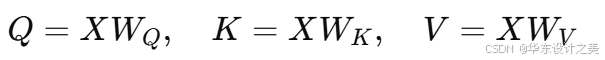
单头注意力计算公式：

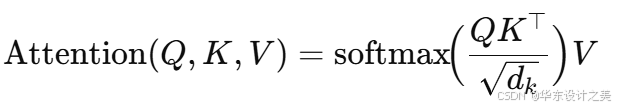
为序列中每个位置分配对其他位置的“注意力权重”，再用这些权重对值 做加权求和，从而实现信息融合。缩放因子 用以稳定 softmax 的梯度。

2.多头注意力（muti-head attention）

不是只用一个注意力头，而是并行使用 h 个头，每个头在较低维空间学习不同子空间的关系，最后再拼接并线性映射回原维度：

这增加了模型表达能力，能同时关注不同类型的关系（如短距 vs 远距、语法 vs 语义等）。

3.位置编码（position encoding）

因为注意力对位置信息不敏感，Transformer 需要显式注入序列位置信息。常见方式：

• 经典正弦/余弦位置编码（固定、可推广到任意长度）

• 可学习的位置向量（learned positional embeddings）

• 相对位置编码（Transformer-XL、T5 等使用，能更好处理长序列）

4.前馈网络（feed forward）

每个注意力模块后通常接一个逐位置的两层前馈网络（带非线性，如 ReLU 或 GELU），形式上：

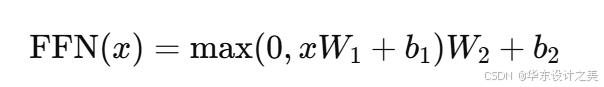
它在每个位置独立变换表示，扩展模型的非线性能力。

5.残差连接 + 归一化（Residual + LayerNorm）

每个子层（多头注意力或 FFN）都有残差连接并接 LayerNorm，常见结构：

y = LayerNorm(x + SubLayer(x))

（也有 pre-norm/ post-norm 两种变体，pre-norm 在深层 Transformer 中更稳定）

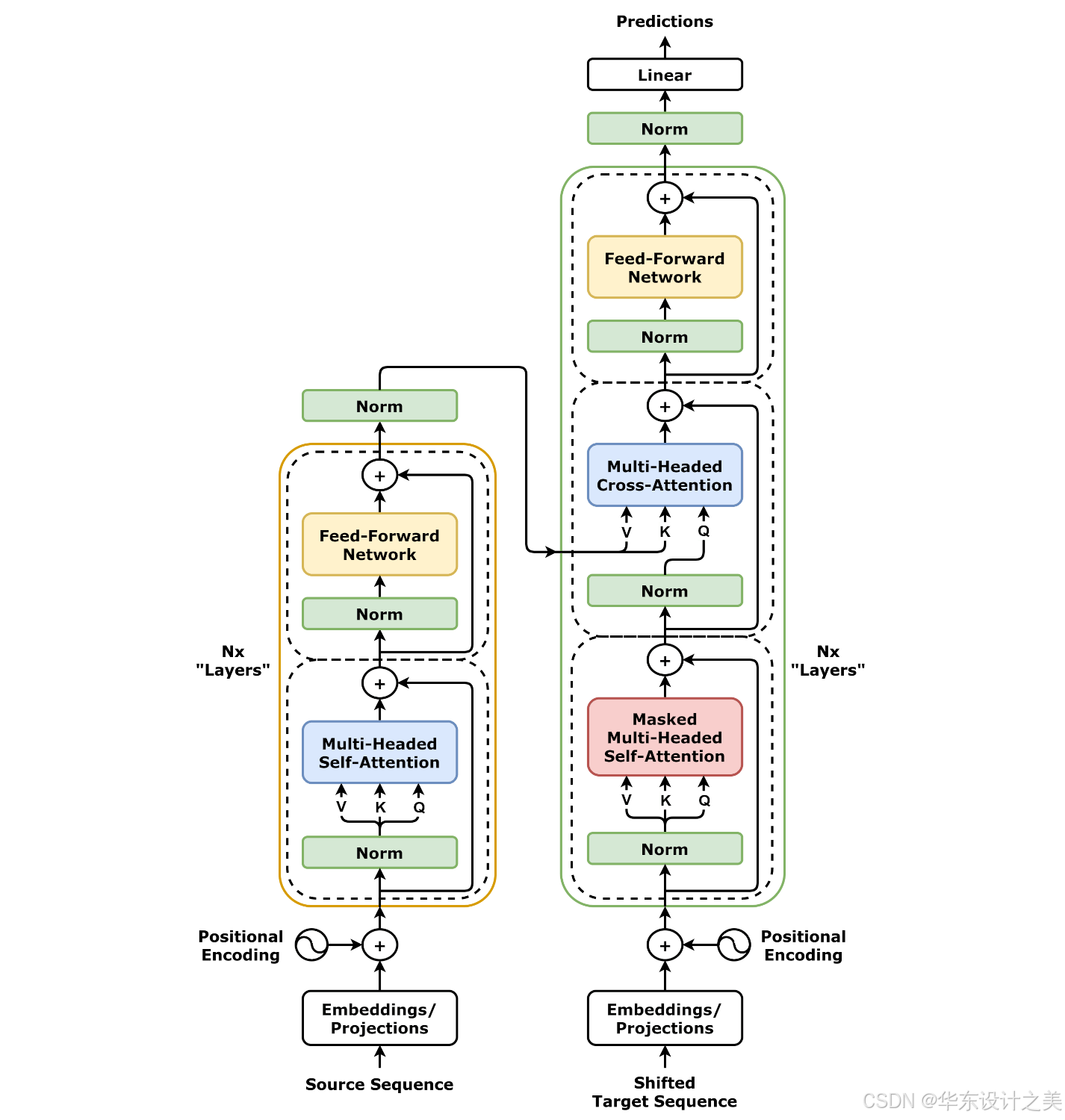
6. 编码器 / 解码器结构

• Encoder：若干个 Encoder Block（Self-Attention → FFN）

• Decoder：在自回归生成场景下，Decoder 包含掩码自注意力（prevent looking ahead）、编码器-解码器注意力（cross-attention）、FFN不同的模型会使用完整 encoder-decoder（如原始 Transformer、T5）、只 encoder（如 BERT）或只 decoder（如 GPT）。

目前常见特征问题

• 注意力矩阵计算复杂度为O(n^2)（序列长度平方），这是 Transformer 在超长序列上的主要瓶颈。

• 并行性：与 RNN 相比，Transformer 的每一层可以并行计算序列中所有位置，因此训练时能充分利用 GPU/TPU 的并行算力。

• 常见训练配方：Adam/AdamW、学习率预热（warmup）+衰减、dropout、权重衰减、混合精度训练等。

变种与改进

• BERT：双向 encoder，采用 Masked Language Modeling（MLM），用于表示学习与下游微调。

• GPT 系列：解码器结构，基于自回归 LM，擅长生成与 few-shot 学习（prompting）。

• T5：把所有 NLP 任务都统一为文本到文本的格式（encoder-decoder）。

• ViT（Vision Transformer）：把图像切成 patch，并用 Transformer 模型处理，成功把 Transformer 引入视觉任务。

• Transformer-XL、Reformer、Longformer、Linformer、Performer 等：为降低自注意力的平方复杂度或扩展上下文长度而提出的各种高效注意力或局部/稀疏/线性近似方法。

• MoE（Mixture of Experts）：在大型模型中通过稀疏路由只激活部分子网络以提高参数利用率与效率。

• Multimodal Transformer：将文字、图像、音频等融合进统一架构（如 Flamingo、CLIP 的某些变体、GPT-4 的多模态方向）。

目前最大创新

把“注意力”作为序列建模的中心机制，从而实现并行、高效地建模任意位置间的长程依赖，并因此彻底改变了模型训练范式 —— 使得大规模预训练 + 下游微调/提示学习成为可能。

• 摆脱序列递归依赖：RNN 依赖时间步的顺序计算（难以并行），而注意力允许在同一层同时查看整个序列，从而大幅提升训练效率。

• 灵活建模长程依赖：注意力能在一个或少数层中直接建立任意两点之间的连接，不再需要逐步传播信息，解决了长距离信息传递的困难。

• 可扩展的预训练范式：Transformer 的结构易于扩展参数规模（深度、宽度、头数），并配合海量数据推动模型能力随规模增长而显著提升（推动了大模型时代）。

• 通用性强：同一基本模块能被改造成 encoder-only、decoder-only、encoder-decoder，甚至跨模态的统一结构，因而被广泛移植到不同领域（NLP、CV、语音、代码、科学数据等）。

激活函数：

• ReLU（Rectified Linear Unit）

  • 公式：ReLU(x) = max(0, x)

  • 优点：计算简单，不饱和，稀疏激活

  • 缺点：死神经元（负区间梯度为 0）

  • 用场景：大多数深层网络（尤其 CNN）

• Leaky ReLU / Parametric ReLU

  • 公式：LeakyReLU(x) = max(αx, x)（α 很小，常 0.01）

  • 用来缓解 ReLU 的“死区”问题

• GELU（Gaussian Error Linear Unit）

  • 近似公式：GELU(x) ≈ 0.5 x [1 + tanh( sqrt(2/π) (x + 0.044715 x^3) )]

  • 直观：x 按概率被保留（比 ReLU 更平滑）

  • 用场景：Transformer（例如 BERT 使用 GELU）

• Sigmoid

  • 公式：σ(x) = 1/(1+e^{-x})

  • 用于二分类输出（概率）或门控单元（RNN）

  • 缺点：饱和区梯度消失

• Tanh

  • 公式：tanh(x) = (e^x - e^{-x})/(e^x + e^{-x})

  • 输出在 [-1,1]，常用于传统 RNN

• Swish

  • 公式：Swish(x) = x * sigmoid(x)

  • 平滑、在某些任务上优于 ReLU

• Softmax

  • 公式（向量 z 的第 i 分量）：

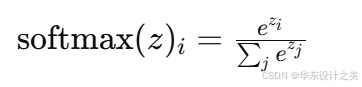
  • 用于多分类最后一层输出概率分布

反向传播：

• 目标：最小化损失函数 L(θ)L(θ)L(θ)，通过链式法则计算损失对每个参数的导数 ∂L∂θ\frac{∂L}{∂θ}∂θ∂L​；

• 从输出层开始反向传播，逐层应用链式法则更新梯度；

• 常用优化器：SGD、Momentum、Adam、AdamW（Transformer 常用 AdamW）。

反向传播顺序：

• 前向：计算每个层的输出与中间缓存（如 Q,K,V、注意力权重、LayerNorm 的均值方差）

• 反向：从损失 dL/dout 开始，按保存的中间值逐步计算 dL/dparams

• 更新：用优化器规则（如 Adam）把参数沿梯度方向更新

梯度：

• 梯度爆炸：大型网络或 RNN 中可能出现，可用梯度裁剪（clip-by-norm）限制梯度范数

• 梯度消失：激活函数（sigmoid/tanh）或非常深的网络会导致，可用 ReLU/GELU、残差结构（ResNet/Transformer）缓解

• LayerNorm / BatchNorm：归一化层能稳定训练，但 Transformer 中常用 LayerNorm（与 BatchNorm 不同）

• 学习率调度：warmup + decay 在 Transformer 中非常重要

CNN卷积神经网络特点：

• 局部感受野（Local receptive field）：卷积核只看局部区域，适合提取局部模式（如边缘、角点）

• 权重共享：同一卷积核在各位置共享参数，显著减少参数并捕捉平移不变特征

• 下采样 / 池化（Pooling）：减小空间尺寸、聚合信息、增强平移不变性

• 平移不变性 / 平移等变性：特征能在空间上平移仍被检测到

• 层次化特征：低层提边缘、纹理，高层提物体部件和语义

• 计算高效：卷积替代全连接，参数节约并利于局部模式学习

CNN 常用于：图像分类、检测、分割、视频分析、某些时序信号（1D 卷积）等。

设计场景题：设计一个基于 Transformer 的多模态系统，用于实时检测市场中的“微结构异常”与“潜在操纵行为”，系统需结合交易级别时序数据、K 线（OHLCV）、新闻文本、社交媒体情绪以及衍生品订单簿信息。请给出架构设计、训练/推理流程、评估指标，以及潜在风险与合规考虑。

• 数据层

  • 高频交易序列：逐笔成交与委托（time, price, size, side）

  • OHLCV（秒/分/小时）

  • 微博/推特/新闻文本流（time-aligned）

  • 衍生品（期货 / 期权）订单簿 snapshot

  • 公司公告 / 财报（结构化文本）

• 特征工程 / embedding

  • 数值序列：标准化、差分、对数收益、波动率窗口特征

  • 序列化：把逐笔序列切成滑动窗口（长度 L），每步包含一组向量

  • 文本 embedding：用预训练语言模型（BERT / 双向 encoder）得到时间切片的情绪向量

  • 事件 embedding：把公告/财报事件编码为类别向量

• 模型架构

  • 多模态 Transformer（或 Cross-Attention）

    • 模块 A：处理高频数值序列（专门的时间卷积或局部注意力）

    • 模块 B：处理文本情绪序列（BERT 提取后下游 Transformer）

    • 跨模态交互：用 cross-attention 把文本向量与数值序列对齐

  • 输出 heads：

    • 二分类 head（是否异常）

    • 多标签 head（异常类型：闪崩、刷单、层级操纵）

    • 回归 head（异常强度评分）

• 训练策略

  • 正负样本不平衡：用过采样、损失加权、Focal Loss

  • 半监督 / 弱监督：用规则或专家标注生成弱标签，再用 RAG / 人工审查校正

  • 在线学习：模型需支持增量更新以适应市场分布漂移

• 评估指标

  • 检测：Precision/Recall/F1、AUC-ROC

  • 误报成本：经济损失函数（误报导致调查成本）

  • 反应时延：从异常发生到被检测的平均延时

  • 解释性：规则回放 / attention 可视化以辅助合规审核

• 风险与合规

  • 数据隐私与合规：交易数据/用户数据的存储与访问控制

  • 偏差与滥用：模型误判可能引发监管调查或市场干扰

  • 可解释性需求：对于关键告警需能提供可审计的证据链

• 部署与监控

  • 流式推理 pipeline（低延迟）

  • 阈值触发人工复核（Human-in-the-loop）

  • 模型漂移监控（概念漂移检测）

• 实验设计建议

  • A/B test：对比是否加入文本情绪能显著提升早期检测率

  • 消融实验：移除 cross-attention 或文本模块评估性能下降

  • 回测仿真：把检测算法回放到历史数据，计算经济指标（如避免的损失）

java实现一道题目：

给定人数和体重，一次性运送人到河流对岸，每条小船最多坐两个人，并且有重量限制，求租用最少需要船的数目。

贪心解法（排序 + 双指针）

对体重数组排序后使用双指针：

• 令 i 指向最轻的人（左端），j 指向最重的人（右端）。

• 若 weights[i] + weights[j] <= limit，则最轻与最重可以同船：i++, j--，消耗 1 条船。

• 否则最重那个人必须单独占一辆：j--，消耗 1 条船。

• 重复直到 i > j。这样能保证最少条数（把尽量重的人与尽量轻的人配对）。

时间复杂度：排序 O(n log n)，双指针 O(n) → 总体 O(n log n)。空间复杂度：O(1)（不计排序的栈/额外空间）。

import java.io.*;
import java.util.*;/*** 最少使用小船数目（每条船最多坐 2 人，且有承重上限 limit）** 输入格式示例（stdin）：* n limit* w1 w2 w3 ... wn** 例如：* 6 100* 70 50 80 50 50 40** 输出：* 最少小船数（整数）*/
public class MinBicycles {public static int minBicycles(int[] weights, int limit) {Arrays.sort(weights);int i = 0, j = weights.length - 1;int bikes = 0;while (i <= j) {if (i == j) { // 仅剩1人bikes++;break;}if (weights[i] + weights[j] <= limit) {// 最轻与最重可以同小船i++;j--;bikes++;} else {// 最重单独一小船j--;bikes++;}}return bikes;}public static void main(String[] args) throws Exception {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));String first = br.readLine();if (first == null || first.trim().isEmpty()) {System.err.println("请按格式输入：n limit");return;}String[] parts = first.trim().split("\\s+");int n = Integer.parseInt(parts[0]);int limit = Integer.parseInt(parts[1]);int[] weights = new int[n];String line = br.readLine();if (line == null || line.trim().isEmpty()) {System.err.println("请在第二行输入 n 个体重（用空格分隔）");return;}String[] ws = line.trim().split("\\s+");if (ws.length < n) {// 允许分多行输入List<Integer> list = new ArrayList<>();for (String s : ws) if (!s.isEmpty()) list.add(Integer.parseInt(s));while (list.size() < n) {String more = br.readLine();if (more == null) break;for (String s : more.trim().split("\\s+")) if (!s.isEmpty()) list.add(Integer.parseInt(s));}for (int i = 0; i < n; i++) weights[i] = list.get(i);} else {for (int i = 0; i < n; i++) weights[i] = Integer.parseInt(ws[i]);}int ans = minBicycles(weights, limit);System.out.println(ans);}
}

输入：

6 100
70 50 80 50 50 40

处理：
排序后：[40,50,50,50,70,80]
配对：

• 80 单独（80 + 40 > 100） -> 1 辆

• 70 + 30?（没有 30）70 + 50 >100 -> 70 单独 -> 第二辆

• 50 + 50 <=100 -> 第三辆

• 剩 40 -> 第四辆
  实际上根据算法，输出 4。

java实现KNN分类器

import java.util.*;/*** 简单手撕 k-NN 分类器（Java）** 说明：* - X_train: m x d 训练数据* - y_train: m 长度整数标签（支持多类）* - k: 邻居数*/
public class SimpleKNN {private double[][] X; // 训练特征private int[] y;      // 训练标签private int n;        // 训练样本数private int d;        // 特征维度// 标准化参数（可选）private boolean normalized = false;private double[] mean;private double[] std;public enum DistMetric { L2, L1 }private DistMetric metric = DistMetric.L2;private boolean useWeighted = false; // 是否按距离加权投票private double eps = 1e-8; // 防止除零// ---------- 构造 ----------public SimpleKNN(int k, DistMetric metric, boolean weighted, boolean normalized) {if (k <= 0) throw new IllegalArgumentException("k must be > 0");this.k = k;this.metric = metric;this.useWeighted = weighted;this.normalized = normalized;}// k 是可变参数（保存在实例中）private int k;// ---------- 训练（只是记住训练集，并计算归一化参数）----------public void fit(double[][] X_train, int[] y_train) {if (X_train == null || y_train == null) throw new IllegalArgumentException("Null data");if (X_train.length != y_train.length) throw new IllegalArgumentException("X and y size mismatch");this.X = X_train;this.y = y_train;this.n = X_train.length;this.d = X_train.length > 0 ? X_train[0].length : 0;if (normalized) {mean = new double[d];std = new double[d];// compute meanfor (int j = 0; j < d; j++) {double s = 0;for (int i = 0; i < n; i++) s += X[i][j];mean[j] = s / n;}// compute std (use population std, add eps to avoid zero)for (int j = 0; j < d; j++) {double s2 = 0;for (int i = 0; i < n; i++) {double diff = X[i][j] - mean[j];s2 += diff * diff;}std[j] = Math.sqrt(s2 / n) + eps;}// normalize training data in-place (optional: could keep original)for (int i = 0; i < n; i++) {for (int j = 0; j < d; j++) {X[i][j] = (X[i][j] - mean[j]) / std[j];}}}// 如果 k 大于样本数，则调整if (k > n) k = n;}// ---------- 距离计算 ----------private double distance(double[] a, double[] b) {if (metric == DistMetric.L2) {double s = 0;for (int i = 0; i < d; i++) {double diff = a[i] - b[i];s += diff * diff;}return Math.sqrt(s);} else { // L1double s = 0;for (int i = 0; i < d; i++) s += Math.abs(a[i] - b[i]);return s;}}// ---------- 单样本预测 ----------public int predictOne(double[] xRaw) {if (X == null) throw new IllegalStateException("Model not fitted");// 归一化输入（如果需要）double[] x = xRaw;if (normalized) {x = new double[d];for (int j = 0; j < d; j++) x[j] = (xRaw[j] - mean[j]) / std[j];}// 计算到所有训练点的距离Neighbor[] neighs = new Neighbor[n];for (int i = 0; i < n; i++) {double dist = distance(x, X[i]);neighs[i] = new Neighbor(i, dist, y[i]);}// 按距离排序（升序）Arrays.sort(neighs, Comparator.comparingDouble(o -> o.dist));// 若出现距离为0（完全相同点），直接返回其标签（避免除零）if (neighs[0].dist <= eps) return neighs[0].label;// 投票（普通或加权）Map<Integer, Double> vote = new HashMap<>();for (int i = 0; i < k; i++) {Neighbor nb = neighs[i];double w = useWeighted ? 1.0 / (nb.dist + eps) : 1.0; // 权重vote.put(nb.label, vote.getOrDefault(nb.label, 0.0) + w);}// 找最大票数（若并列，选择票数最大的且标签最小者，确保确定性）int bestLabel = -1;double bestScore = -1;for (Map.Entry<Integer, Double> e : vote.entrySet()) {int lbl = e.getKey();double sc = e.getValue();if (sc > bestScore || (sc == bestScore && lbl < bestLabel)) {bestScore = sc;bestLabel = lbl;}}return bestLabel;}// ---------- 批量预测 ----------public int[] predict(double[][] Xtest) {int m = Xtest.length;int[] out = new int[m];for (int i = 0; i < m; i++) out[i] = predictOne(Xtest[i]);return out;}// ---------- 辅助类 ----------private static class Neighbor {int idx;double dist;int label;Neighbor(int idx, double dist, int label) { this.idx = idx; this.dist = dist; this.label = label; }}// ---------- 演示 main ----------public static void main(String[] args) {// 构造一个简单的2D数据集（两簇）double[][] Xtrain = {{1.0, 1.0}, {1.2, 0.8}, {0.8, 1.1}, // 类别 0{4.0, 4.0}, {3.9, 4.1}, {4.2, 3.8}  // 类别 1};int[] ytrain = {0, 0, 0, 1, 1, 1};double[][] Xtest = {{1.1, 1.0}, {4.1, 3.9}, {2.5, 2.5}};// 实例化 k-NN（k=3，L2 距离，weighted=false，normalized=true）SimpleKNN knn = new SimpleKNN(3, DistMetric.L2, false, true);knn.fit(Xtrain, ytrain);int[] preds = knn.predict(Xtest);System.out.println("Predictions:");for (int i = 0; i < preds.length; i++) {System.out.printf("x=%s -> %d%n", Arrays.toString(Xtest[i]), preds[i]);}// 测试加权投票（距离加权）SimpleKNN knnWeighted = new SimpleKNN(3, DistMetric.L2, true, true);knnWeighted.fit(Xtrain, ytrain);int[] pw = knnWeighted.predict(Xtest);System.out.println("Predictions (weighted): " + Arrays.toString(pw));}
}

• 为什么要归一化？
  距离受特征量级影响大，若某个特征量级远大，会主导距离，标准化（z-score）能避免此问题。

• k 的选择？

  • k 太小：对噪声敏感（高方差）

  • k 太大：可能把不同类混合（高偏差）
    常用交叉验证（如 5-fold）选取最优 k。

• 复杂度与优化

  • 朴素实现：每次预测计算到所有训练点距离 → O(n·d)（按 sort 额外 O(n log n)）。

  • 可用 KD-tree、Ball-tree、或近似最近邻（LSH、Faiss）在高维或大数据上加速，但 KD-tree 在高维退化。

  • 若需要高吞吐，可向量化或并行化距离计算。

• 多分类投票策略

  • 普通投票（多数表决）

  • 加权投票（距离越近权重越高）

  • 如果 tie，常做 deterministic tie-break（最小标签）或随机化。

• 处理大数据

  • 使用近邻内存索引（Faiss）、倒排/LSH、或者在分布式中做 approximate kNN。