当前位置：首页 > news >正文

【小白笔记】普通二叉树（General Binary Tree）和二叉搜索树的最近公共祖先（LCA）

news 2025/10/19 15:47:45

普通二叉树（General Binary Tree）的最近公共祖先（LCA）问题。

“人话”解释：二叉树的最近公共祖先 (LCA)

1. 概念背景：树就是家谱（家谱）

二叉树 (Binary Tree)：你可以把它想象成一个只有亲生父母和两个孩子的家谱。
- 根节点 (Root)：就是太祖爷爷/奶奶，辈分最高的那位。
- 子节点：就是晚辈。
- 父节点：就是长辈。
- 节点的值 (Value)：就是每个家庭成员的名字或编号。
祖先 (Ancestor)：在你的家谱里，你的爸爸、爷爷、曾祖父等等，所有辈分比你高、在你的直系血缘路径上的长辈，都是你的祖先。

2. 题目核心：找“共同的、最年轻的长辈”（最近的公共祖先）

题目要求我们找出两个指定的家庭成员 $p$ 和 $q$ 的 最近公共祖先 $x$ 。

“最近公共祖先”的“人话”理解就是：

找到 $p$ 和 $q$ 两人“共同的长辈”中，离他们血缘关系最近、辈分最低的那一位。

换句话说，这位 $x$ 满足两个条件：

公共 (Common)： $x$ 必须同时是 $p$ 的祖先，也是 $q$ 的祖先。
最近 (Least/Deepest)：在所有满足条件 1 的祖先中， $x$ 必须是辈分最低（即深度最大，离 $p$ 和 $q$ 最近）的那一位。

特殊情况：节点可以是自己的祖先。

如果 $p$ 就是 $q$ 的爷爷，那么 $p$ 和 $q$ 的公共祖先有 $p$ 、曾祖父、太祖父等。根据“最近”原则，爷爷 $p$ 就是最近公共祖先。

3. 示例分析（将家谱图可视化）

示例 1 来理解：
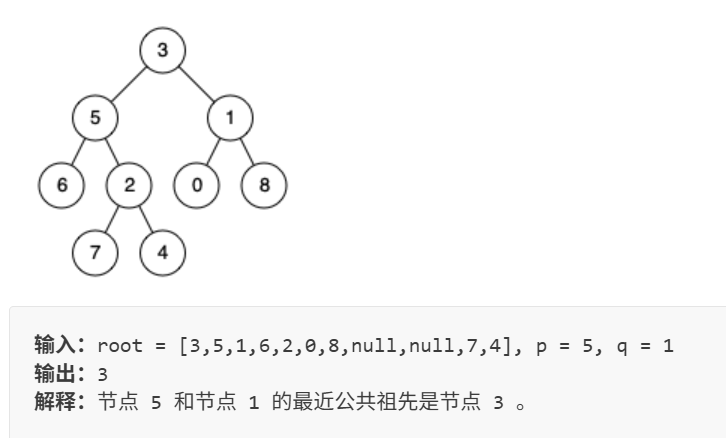
在这里插入图片描述

家谱： 3 是太祖父，5 和 1 是他的孩子……
任务： 找 $p = 5$ 和 $q = 1$ 的 LCA。

$p = 5$ 的祖先：5 本身，3。
$q = 1$ 的祖先：1 本身，3。
公共祖先：3。
最近公共祖先：只有 3，所以是 3。

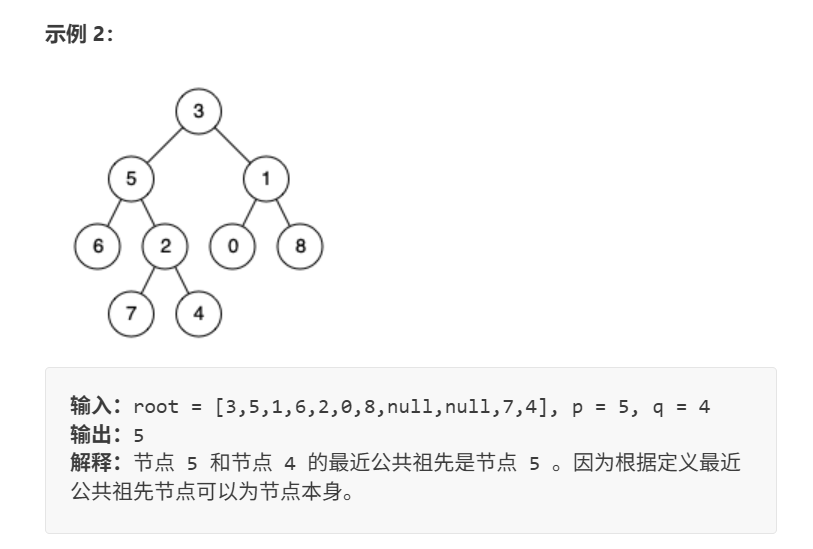
在这里插入图片描述

任务： 找 $p = 5$ 和 $q = 4$ 的 LCA。

$p = 5$ 的祖先：5 本身，3。
$q = 4$ 的祖先：4 本身，2，5，3。
公共祖先：5，3。
最近（辈分最低，离他们最近）：是 5。

二叉树和二叉搜索树的区别

二叉树 (Binary Tree) 和 二叉搜索树 (Binary Search Tree, BST) 都是树形结构，但它们最大的区别在于节点值的排列规则。

特性	二叉树 (Binary Tree)	二叉搜索树 (Binary Search Tree, BST)
定义	每个节点最多有两个子节点（左子节点和右子节点）。	是一种特殊的二叉树。
规则	无特殊的节点值排列规则。左子节点的值可以大于或小于根节点。	有严格的排列规则（有序性）： 1. 左子树规则：左子树中所有节点的值都小于根节点的值。 2. 右子树规则：右子树中所有节点的值都大于根节点的值。
用途	表达层次关系（如家谱、文件系统、表达式）。	用于高效地查找、插入、删除数据。
LCA 算法	必须遍历整个树（DFS 递归），时间复杂度 $O (N)$ 。	可利用有序性，直接判断搜索方向，时间复杂度 $O (H)$ （ $H$ 为树高）。

总结： 二叉树是模板，二叉搜索树是带了“左小右大”规则的特殊模板。

二叉搜索树的最近公共祖先 (LCA)

在 BST 中查找 LCA 之所以高效，正是利用了其有序性。

1. 算法核心思路（复习）

从根节点 $roo t$ 开始，不断向下遍历，直到找到第一个分岔点，即为 LCA：

分岔点/命中 $p$ 或 $q$ ：
- 如果 $p$ 和 $q$ 分别位于 $roo t$ 的左子树和右子树（即 $p$ 和 $q$ 的值一个小于 $roo t$ 一个大于 $roo t$ ），那么 $roo t$ 就是它们最近的分叉点，即 LCA。
- 如果 $roo t$ 本身就是 $p$ 或 $q$ ，那么 $roo t$ 也是 LCA。
- 此时，停止遍历，返回 $roo t$ 。
都往左走：
- 如果 $p$ 和 $q$ 的值都小于 $roo t$ 的值，说明 LCA 必然在左子树中，向左子树继续搜索。
都往右走：
- 如果 $p$ 和 $q$ 的值都大于 $roo t$ 的值，说明 LCA 必然在右子树中，向右子树继续搜索。

2. 示例分析

我们用您提供的树 $roo t = [6, 2, 8, 0, 4, 7, 9, n u ll, n u ll, 3, 5]$ 来验证：

树的结构：

      6/   \2     8/ \   / \0   4 7   9/ \3   5

示例 1: $p = 2, q = 8$

从 $roo t = 6$ 开始：
- $p = 2 < 6$
- $q = 8 > 6$
- 决策： $p$ 在左， $q$ 在右，分居两侧。
结果： $6$ 就是 $2$ 和 $8$ 的 LCA。

示例 2: $p = 2, q = 4$

从 $roo t = 6$ 开始：
- $p = 2 < 6$
- $q = 4 < 6$
- 决策： $p$ 和 $q$ 都在左侧。向左搜索，current 移动到 $2$ 。
从 $c u rre n t = 2$ 开始：
- $p = 2$ （等于 $c u rre n t$ ）
- $q = 4 > 2$
- 决策： $p$ 和 $q$ 不再位于同一侧（因为 $p$ 命中 $c u rre n t$ ）， $2$ 就是 $2$ 和 $4$ 的 LCA。
结果： $2$ 就是 $2$ 和 $4$ 的 LCA。

这个高效的算法就是利用了 “左小右大” 的规则，每一步都排除了大约一半的搜索范围，因此非常快速。

使用 Python 语言来实现刚才介绍的二叉搜索树 (BST) 中查找最近公共祖先 (LCA) 的迭代算法。

Python 代码实现

我们首先定义 TreeNode 类来构建二叉树的节点，然后实现 lowestCommonAncestor 方法。

class TreeNode:"""定义二叉树的节点结构。"""def __init__(self, val=0, left=None, right=None):self.val = valself.left = left  # 指向左子节点的引用self.right = right # 指向右子节点的引用class Solution:"""解决 BST 最近公共祖先问题的类"""def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':"""在二叉搜索树中找到两个给定节点 p 和 q 的最近公共祖先。Args:root: 树的根节点。p: 目标节点之一。q: 目标节点之二。Returns:p 和 q 的最近公共祖先节点。"""# 使用迭代 (循环) 方式current = root# 只要当前节点非空，就继续搜索while current is not None:# 1. 如果 p 和 q 的值都小于 current.val：# 说明它们都在左子树中，LCA 在左侧if p.val < current.val and q.val < current.val:# 向左移动current = current.left# 2. 如果 p 和 q 的值都大于 current.val：# 说明它们都在右子树中，LCA 在右侧elif p.val > current.val and q.val > current.val:# 向右移动current = current.right# 3. 命中 LCA：# 如果不属于以上两种情况，说明 p 和 q 必定分居在 current 的两侧（一左一右），# 或者 current 自身就是 p 或 q。# 在 BST 中，这两种情况都意味着 current 就是最近公共祖先。else:return current# 理论上 p 和 q 均存在于树中时，不会执行到这里return None

1. 代码是在搜索什么？

1.“# 只要当前节点非空，就继续搜索… 这是在搜索啥呢？”

这段代码的整个 while 循环过程，核心目标是在搜索：

目标：第一个分叉点（The First Split Point）。

用“人话”来说：

搜索的过程，就是从根节点（辈分最高者）开始，不断向下追溯 $p$ 和 $q$ 的血缘路径，直到找到他们俩的路径第一次分开的那位祖先。

为什么是“分叉点”？

如果 $p$ 和 $q$ 都在左边：说明它们在 $c u rre n t$ 这里还没有分叉，它们的 LCA 肯定在左边的子孙中，所以我们继续向左追。
如果 $p$ 和 $q$ 都在右边：同理，它们在这里还没有分叉，继续向右追。
如果 $p$ 和 $q$ 分居两侧：说明 $c u rre n t$ 就是它们路径第一次分开的地方。 $p$ 走左边， $q$ 走右边。那么 $c u rre n t$ 就是它们最近的公共祖先。
如果 $c u rre n t$ 就是 $p$ 或 $q$ ：假设 $c u rre n t = p$ 。由于 $q$ 存在于树中且 $\ne p$ ，所以 $q$ 必然是 $p$ 的子孙或在 $p$ 的另一侧。无论哪种情况，祖先链到 $p$ 已经结束， $p$ 就是它们最近的公共祖先。

所以，整个 while 循环就是在执行一个排查过程：排除所有 $p$ 和 $q$ 路径上共同的、比 LCA 辈分更高的祖先，直到遇到那个“辈分最低”的共同祖先，即 LCA。

2. `current` 变量的功能是什么？

current 变量的核心功能就是追踪当前的搜索位置**，扮演着临时祖先和当前观察点的角色。

`current` 的功能解析：

当前观察点：
- current 始终指向我们当前正在判断的那个节点。
- 我们通过检查 current.val 与 $p . v a l$ 和 $q . v a l$ 的关系，来决定下一步的搜索方向。
临时祖先：
- 在任何时刻，从根节点到 current 之间的所有节点，都是 $p$ 和 $q$ 的潜在公共祖先（如果 $p$ 和 $q$ 都在 current 为根的子树中）。
- 我们正在做的事情，就是从这串祖先中，找到那个最接近 $p$ 和 $q$ 的。
可以移动 (它是指针/引用)：
- 可以移动。 current 在 Python 中是一个引用（Reference），它存储了某个 TreeNode 对象的内存地址。
- 当执行 current = current.left 或 current = current.right 时，我们并没有改变原来的节点，而是改变了 current 这个引用变量，让它指向了树中的下一个节点。
- 在 BST-LCA 算法中，这种移动是单向的（只向下走），绝不会向上回溯，这是它比普通二叉树 LCA 更快的原因。

示例 2 的 `current` 追踪：

步骤	`current` 节点	`current.val`	决策过程	`current` 下一步
开始	$6$ (Root)	$6$	$p (2) < 6$ 且 $q (4) < 6$	`current = current.left`
第一次循环	$2$	$2$	$p (2)$ 等于 $c u rre n t . v a l$ ，命中 LCA	返回 $2$

可以看到，current 从 $6$ 移动到了 $2$ ，每次移动都是在收紧**“潜在 LCA 区域”**，直到最终锁定 $2$ 为止。

在 Python 代码中，p.val、q.val 和 current.val 确实是 Python 面向对象编程 (Object-Oriented Programming, OOP) 中的标准写法，用来访问对象（Object）的属性（Attribute）。

解释 1：`.val` 在 Python 代码中的含义

在 Python 中，当您看到 对象名.属性名 这样的结构时，它表示您正在访问该对象内部存储的某个数据。

在这个 LCA 的代码中：

p、q、current 都是 TreeNode 类创建出来的对象（即树上的一个节点）。
.val 就是这些对象的一个属性，它存储了该节点所代表的数值。

代码片段	含义（人话）	对应数据结构定义
`p.val`	节点 $p$ 里面存储的那个值（比如 3、5、7）。	`self.val = val`
`q.val`	节点 $q$ 里面存储的那个值。	`self.val = val`
`current.val`	当前正在观察的节点 `current` 里面存储的值。	`self.val = val`
`current.left`	当前节点 `current` 的左子节点（是一个完整的 `TreeNode` 对象）。	`self.left = left`

解释 2：为什么必须使用 `.val`？

在 Python（以及大多数面向对象语言）中，p 和 q 这两个变量存储的是整个节点对象（包含了值、左指针、右指针等）。

我们不能直接写 if p < current，因为 Python 不知道该用 $p$ 的哪个部分和 $c u rre n t$ 进行比较。

为了进行数值比较（判断左还是右），我们必须精确地告诉程序：请取出 $p$ 节点内部的那个数值属性 (val) 来进行比较。

这就是为什么我们需要使用 p.val 来取出节点中的数值。

示例回顾与人话翻译

我们再次回顾那段代码，用更自然的方式理解它在做什么：

# 1. 如果 p 和 q 的值都小于 current.val：
if p.val < current.val and q.val < current.val:# 向左移动current = current.left# 人话翻译：
# 检查：
# (p 节点里面的值)  小于  (当前节点里面的值) 
# AND
# (q 节点里面的值)  小于  (当前节点里面的值)
# 如果都成立，说明 p 和 q 都在左边，那么当前观察点 (current) 就要**换成**它的左子节点。

总结来说，p.val 不是 Python 的特殊语法，它只是访问对象属性的标准方式，确保我们比较的是树节点中的数值内容，而不是节点对象本身。

递归实现 (作为对比和拓展)

虽然迭代实现更高效（ $O (1)$ 空间），但递归实现也十分简洁，体现了 DFS 的思想：

class SolutionRecursive:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':# 递归的当前节点if root is None:return None# 1. 都在左侧if p.val < root.val and q.val < root.val:return self.lowestCommonAncestor(root.left, p, q)# 2. 都在右侧elif p.val > root.val and q.val > root.val:return self.lowestCommonAncestor(root.right, p, q)# 3. 命中 LCA (分居两侧 或 root 就是 p/q)else:return root

对比：

迭代法 (Iteration)：空间复杂度 $O (1)$ ，效率略高。
递归法 (Recursion)：空间复杂度 $O (H)$ （ $H$ 为树高，由递归栈产生），代码逻辑更贴近思考过程。

在 BST 中，两者都是非常优秀的解法。这段代码是二叉搜索树（BST）中查找最近公共祖先（LCA）的经典迭代实现，非常值得掌握！记忆它不应该靠死记硬背，而是理解背后的逻辑推理。

我为您总结了一个逻辑记忆法，分为三个部分。

记忆法核心：将代码转化为“决策树”

核心在于理解 BST 的特性如何帮助我们在每一步做决策。LCA 的寻找过程，就是从根节点开始，根据 $p$ 和 $q$ 的值，不断做出“左转”、“右转”或“停下”的决策。

第一步：记忆 `TreeNode` 类的结构

这部分是基础，必须清楚一个树节点包含什么。

记忆点	代码	意义（人话）	记忆口诀
自身的值	`self.val = val`	节点里存储的数据。	节点有数据（`val`）。
左子树连接	`self.left = left`	指向左边“下一代”的引用。	左边有儿子（`left`）。
右子树连接	`self.right = right`	指向右边“下一代”的引用。	右边有儿子（`right`）。

记忆核心： 树节点是父子关系的纽带，所以它必须知道自己是谁（val），以及自己的左儿子（left）和右儿子（right）在哪里。

第二步：记忆 `lowestCommonAncestor` 的主体框架

这部分是迭代（循环）的标准模式。

记忆点	代码	意义（人话）	记忆口诀
初始化	`current = root`	从根节点开始，当前节点是我们观察的位置。	从头开始（`root`）。
循环条件	`while current is not None:`	只要树还没走完（没走到空），就继续找。	没走到底就一直找（`while`）。
迭代推进	`current = current.left / current.right`	根据决策，将观察位置向下移动。	沿着路往下走（`current = next`）。

记忆核心： LCA 是一个自顶向下的查找过程，所以使用一个 current 指针从 root 开始，不断循环更新 current，直到找到结果为止。

第三步：记忆 LCA 的决策逻辑（最关键）

这部分是利用 BST 特性的核心。LCA 算法只需要判断三种情况：

决策 1：继续向左走 (都在左侧)

逻辑推理： 如果 $p$ 和 $q$ 的值都比当前节点 current 的值小，根据 BST 的定义，LCA 绝不可能在右边，只能在左子树。

代码体现：

if p.val < current.val and q.val < current.val:current = current.left # 走向左边

决策 2：继续向右走 (都在右侧)

逻辑推理： 如果 $p$ 和 $q$ 的值都比当前节点 current 的值大，根据 BST 的定义，LCA 绝不可能在左边，只能在右子树。

代码体现：

elif p.val > current.val and q.val > current.val:current = current.right # 走向右边

决策 3：停下，命中 LCA (分居两侧或命中自身)

逻辑推理： 如果不是上面两种情况，说明 $p$ 和 $q$ 不再位于同一侧了。
- 情况 A： $p$ 在左边， $q$ 在右边（或反之）。此时 current 是它们的分叉点，即 LCA。
- 情况 B： current 本身就是 $p$ 或 $q$ 。由于 $p$ 和 $q$ 必然在树中，current 是它们离根最近的公共祖先。
- 结论： 无论哪种情况，current 就是我们要找的 LCA，搜索可以停止。

代码体现：

else:return current # 找到了，返回

总结记忆口诀：

LCA 决策三步走：

都比我小？ $⟹\implies$ 左走！ (current = current.left)
都比我大？ $⟹\implies$ 右走！ (current = current.right)
不左不右？ $⟹\implies$ 停下！（我是 LCA，return current）

通过理解这三个决策背后的 BST 规则，您就能在任何时候重新构建这段简洁而高效的 LCA 代码。

这两段代码的核心原理确实是完全一样的**。它们都是利用了**二叉搜索树（BST）**的“左小右大”特性来寻找 LCA。

它们的主要区别仅仅在于实现方式：

第一段代码是 迭代（Iteration） 实现。
第二段代码是 递归（Recursion） 实现。

我将详细解释它们的原理一致性和实现区别，以及如何从代码结构上看出来。

一、核心原理的一致性

两段代码都遵循完全相同的 BST-LCA 决策逻辑：

决策逻辑	迭代（循环）实现	递归（函数调用）实现
都小于当前节点 $⟹\implies$ 向左走	`current = current.left`	`return self.lowestCommonAncestor(root.left, p, q)`
都大于当前节点 $⟹\implies$ 向右走	`current = current.right`	`return self.lowestCommonAncestor(root.right, p, q)`
分居两侧/命中 $⟹\implies$ 找到 LCA，停止	`return current`	`return root`

无论使用哪种方式，算法执行的路径（从根节点到 LCA 节点的路径）是完全相同的。

二、迭代（Iteration）与递归（Recursion）的区别

虽然原理相同，但在代码的实现结构和资源使用上，它们有着本质的区别。

1. 迭代实现（循环）

特点	代码表现	作用和原理
控制流	使用 `while` 循环	程序在同一个函数内重复执行代码块，通过改变循环变量（`current`）来推进搜索。
前进/移动	`current = current.left`	通过赋值操作，将 `current` 这个指针向下移动。
终止	`return current` 结束 `while` 循环	在函数内找到结果后立即返回。
空间复杂度	$O (1)$	不依赖函数栈。只需要常数级的额外变量 (`current`)。

2. 递归实现（函数调用）

特点	代码表现	作用和原理
控制流	依靠函数自身调用	每次“向下走”一步，都创建一个新的函数调用。
前进/移动	`return self.lowestCommonAncestor(root.left, p, q)`	将子问题（以 $roo t . l e f t$ 为根找 LCA）的解决，委托给下一层函数。
终止	`return root` 结束递归链	当命中结果时，结果会逐层返回给最初的调用者。
空间复杂度	$O (H)$	每次函数调用都会占用函数调用栈（Call Stack）空间，空间消耗取决于树的高度 $H$ 。

结论：如何从代码结构上看出来？

区分点	迭代代码	递归代码
关键字	核心是 `while` 循环。	核心是 `return self.lowestCommonAncestor(...)`，即函数自己调用自己。
推进方式	通过赋值：`current = ...`	通过返回函数调用的结果：`return function(...)`
变量名	通常使用 `current` 或 `node` 作为可变的循环变量。	通常使用 `root` 或 `node`，它在当前函数内是不可变的（指向当前层级的根）。

在解决 BST-LCA 这种路径唯一的问题时，迭代法（ $O (1)$ 空间）通常被认为是更优的实现，因为它避免了递归栈带来的额外空间开销。

普通二叉树不能用 BST 的方法？（难点）

之前做的 BST-LCA 非常简单，因为它利用了有序性（左小右大）。

但如果题目是普通二叉树。

挑战： 节点 5 的左边可能是 100，右边可能是 2。我们不能只看值的大小来决定往左走还是往右走。
解法（人话）： 既然不能直接判断，我们就必须走遍整棵树。我们像一个侦探一样，从太祖爷爷（根节点）出发，去问每一个家庭成员：
- “我的左边有没有 $p$ 和 $q$ ？”
- “我的右边有没有 $p$ 和 $q$ ？”

这就是 DFS 递归方法的核心逻辑：

如果你（当前节点 $roo t$ ）发现：
- 左边找到了 $p$
- 右边找到了 $q$
- 恭喜你，你就是那个分叉点，你就是 LCA！
如果你自己就是 $p$ 或 $q$ 之一，那么你就是 LCA（因为 $p$ 或 $q$ 的另一个肯定在你的子孙中）。

总结来说，这个题目在问你：在给定的家谱里，如何高效地找到两个指定的家族成员，并确定他们俩“共同的、离他们最近”的那位直系长辈？

核心思想（递归法）： 遍历到当前节点时，问它的左子树和右子树：“你们那里有没有找到 $p$ 或 $q$ ？”

如果 左边找到了 $p$ 或 $q$ (返回一个非空节点)。
如果 右边也找到了 $p$ 或 $q$ (返回一个非空节点)。
那么，当前节点 $roo t$ 就是 $p$ 和 $q$ 的分叉点，即 LCA。

Python 代码实现

我们将使用 Python 语言来实现这个经典的递归算法。

class TreeNode:"""二叉树的节点结构定义"""def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution:"""解决普通二叉树最近公共祖先问题的类"""def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':"""通过递归（后序遍历）找到普通二叉树中 p 和 q 的最近公共祖先。Args:root: 当前递归的子树根节点。p: 目标节点之一。q: 目标节点之二。Returns:如果在以 root 为根的子树中找到 p 或 q，则返回找到的那个节点；如果 p 和 q 都找到了，则返回它们的 LCA；如果都没找到，则返回 None。"""# 1. 递归终止条件 (Base Case):# 如果当前节点为空，或者当前节点就是 p 或 q 之一，则返回当前节点。# 如果当前节点是 p/q，它就是 p/q 路径上最深的祖先。if root is None or root == p or root == q:return root# 2. 递归搜索 (Divide):# 递归地在左右子树中查找 p 和 q# left_lca 存储的结果：在左子树中找到的 p 或 q 或它们的 LCA（或 None）left_lca = self.lowestCommonAncestor(root.left, p, q)# right_lca 存储的结果：在右子树中找到的 p 或 q 或它们的 LCA（或 None）right_lca = self.lowestCommonAncestor(root.right, p, q)# 3. 结果合并与判断 (Conquer - 后序遍历的判断时机):# 情况 A: 左右子树都找到了结果（即 left_lca 和 right_lca 都非空）# 这意味着 p 和 q 分别位于 root 的左右子树中。if left_lca is not None and right_lca is not None:# 那么 root 就是它们的分叉点，即 LCA。return root# 情况 B: 只有左子树找到了结果 (right_lca 为 None)# 这意味着 p 和 q（如果都存在）都在左子树中，或者只有 p/q 在左子树。# 无论如何，LCA 都在左边，直接返回左子树找到的结果。elif left_lca is not None:return left_lca# 情况 C: 只有右子树找到了结果 (left_lca 为 None)# 类似地，LCA 在右边，直接返回右子树找到的结果。elif right_lca is not None:return right_lca# 情况 D: 左右子树都没找到 (left_lca 和 right_lca 都是 None)# p 和 q 都不在以 root 为根的子树中，返回 None。else:return None# 简化代码：# if left_lca and right_lca:#     return root# return left_lca if left_lca else right_lca

复杂度分析

时间复杂度 (Time Complexity)： $O (N)$
- $N$ 是树中节点的总数。
- 我们通过 DFS 遍历了树中的每个节点恰好一次，因此时间复杂度是线性的。
空间复杂度 (Space Complexity)： $O (H)$
- $H$ 是树的高度。
- 空间消耗主要来自于递归调用栈的深度。最坏情况下（链表）， $O (N)$ ；最好情况下（平衡树）， $O(log⁡N)O(\log N)$ 。

这段代码是解决普通二叉树 LCA 的核心递归模板，非常重要！记忆它需要理解它遵循的**“后序遍历 + 向上汇报”**逻辑。

普通二叉树 LCA 记忆法：【分队侦察，向上汇报】

这个算法可以想象成：你（程序）派你的两个副手（左右子树）去树里找目标 $p$ 和 $q$ ，然后根据他们的汇报结果来做最终判断。

步骤一：【汇报基线】—— 什么时候停止深入？ (Base Case)

记忆点	代码	侦探人话	核心逻辑
终止条件	`if root is None or root == p or root == q: return root`	“当前节点为空地了（`None`），或者我就是目标 $p$ / $q$ 之一。找到了/走完了，停止深入，把我这个节点返回给我的上级（父节点）。”	如果找到目标，必须立即返回，确保它是最深的公共祖先。

递归算法中最核心的一点：基准情况（Base Case）。

在二叉树的 LCA 递归算法中，if root is None 这个判断考虑的是递归搜索的边界，它有两个主要的意义：

1. 考虑的是“空子树”的边界（最主要的用途）

在递归向下搜索的过程中，root 往往会成为其父节点的一个子节点（parent.left 或 parent.right）。

当一个节点是**叶节点（Leaf Node）**时，它的 left 和 right 都是 None。

当函数调用到 lowestCommonAncestor(leaf.left, p, q) 时，传入的 root 参数就是 None。
这时，程序需要知道该做什么，不能再继续搜索了。

人话解释：

“当我走到一个空地（None）时，说明这条路已经走到底了，这块区域没有 $p$ 也没有 $q$ ，所以我要向上级（父节点）汇报：‘我空手而归，没有找到任何线索。’（即返回 None）”

这个判断确保了递归不会无限地向下调用，是防止程序崩溃（栈溢出）的关键。

2. 考虑的是“空树”的特殊情况（次要用途）

理论上，如果用户传入的整个树就是空的（即调用时 root 本身就是 None）：

lowestCommonAncestor(None, p, q)

那么程序会立即返回 None。虽然题目中提示 $p$ 和 $q$ 必然存在于树中（意味着树至少有两个节点），但从代码的健壮性（Robustness）角度来看，处理根节点为空的情况是标准的做法。

总结：

if root is None: return root（即 return None）的作用就是：

充当递归的“停止阀”。
向上级汇报“未找到”，从而让上级（父节点）能够根据左右两边的汇报结果进行汇总判断。

让我们重新拆解，看看 root 在不同情况下的实际值是什么，以及它如何与“汇报”逻辑完美契合：

重新拆解 `if root is None or root == p or root == q: return root`

这个判断将三种不同的基准情况合并到了一起，但它们返回的 root 的实际意义是不同的：

情况 1：走到空地了（走不通了）

条件满足： root is None
代码执行： return root
实际返回的值： $None\text{None}$
汇报含义： “空手而归，没有找到任何线索。” (对应您的理解)

情况 2：找到目标 $p$ 或 $q$ 之一

条件满足： root == p 或 root == q
代码执行： return root
实际返回的值： 节点 $p$ 或节点 $q$ (一个非空的 TreeNode 对象)
汇报含义： “找到目标了！这就是我能找到离根最深的线索。”

为什么代码要写成 `return root`？

代码将这三种情况写在一起并统一返回 root，是为了简洁和高效：

程序简洁： 避免了写成：

if root is None:return None  # 汇报空手
if root == p or root == q:return root  # 汇报线索

逻辑统一： 无论是返回 $None\text{None}$ 还是返回 $p / q$ ，其目的都是在汇报：
- 返回 $None\text{None}$ ： 表示“这条路径没结果”。
- 返回 $p / q$ ： 表示“这条路径有结果，结果就是这个节点”。

更严谨的表达是：

“如果当前节点是空地（root is None），我们执行 return root。此时 root 的值就是 $None\text{None}$ ，因此实际上是向上级汇报了 $None\text{None}$ （即‘空手而归’）。”

步骤二：【分队侦察】—— 委托左右子树 (Divide)

记忆点	代码	侦探人话	核心逻辑
左边去查	`left_lca = self.lowestCommonAncestor(root.left, p, q)`	“左副手，你去左边找，找到什么回来告诉我。”	递归调用，向左推进。
右边去查	`right_lca = self.lowestCommonAncestor(root.right, p, q)`	“右副手，你去右边找，找到什么回来告诉我。”	递归调用，向右推进。
结果	`left_lca` 和 `right_lca`	这两个变量存储了左右两边“带回来的唯一线索”（找到的 $p$ / $q$ 或它们的 LCA，或者 `None`）。

步骤三：【汇总判断】—— 根据汇报结果决策 (Conquer)

这是整个代码最核心的逻辑，是后序遍历（先左、再右、最后处理根）的应用。根据左右副手的汇报结果，你（root 节点）做出以下四种决策：

决策情况	代码逻辑	侦探人话	结果（LCA）
情况 A：分叉点	`if left_lca is not None and right_lca is not None:`	“左边说找到一个，右边说也找到一个。太棒了！我是它们路径第一次分开的地方！”	返回 `root` (LCA 是我)
情况 B：都在左边	`elif left_lca is not None:`	“只有左边找到了线索。那我知道了，LCA 肯定在左边那个线索的上方。”	返回 `left_lca` (将左边找到的线索原样向上汇报)
情况 C：都在右边	`elif right_lca is not None:`	“只有右边找到了线索。LCA 肯定在右边那个线索的上方。”	返回 `right_lca` (将右边找到的线索原样向上汇报)
情况 D：都没找到	`else:`	“左右都没找到线索，看来 $p$ 和 $q$ 不在我这片区域。”	返回 `None` (向上级汇报：无发现)

手撕总结

用这三句话总结整个流程，就能轻松实现代码：

Stop: 遇到空地或目标，返回自己。
Call: 派左和右去搜。
Judge:
- 左右都带回线索 $⟹\implies$ 我是 LCA。
- 只有一边带回线索 $⟹\implies$ 把线索原样返回（LCA 在更深处）。
- 两边都空手而归 $⟹\implies$ 返回空。

递归 LCA 算法的本质：为什么必须使用后序遍历 (Post-order Traversal) 的处理时机？

答案在于：LCA 的判断依赖于子树的“汇报”结果，而子树的结果必须先于父节点被处理。

核心原因：LCA 问题的“自底向上”决策需求

LCA 问题的决策是自底向上（Bottom-Up）的：

要判断当前节点 $roo t$ 是不是 $p$ 和 $q$ 的 LCA，你必须先知道：
- 左子树有没有找到 $p$ 或 $q$ 。
- 右子树有没有找到 $p$ 或 $q$ 。
只有在左右子树的搜索和汇报全部完成之后，父节点才能做出“我是不是分叉点”的最终决定。

后序遍历的定义是：“左 $→\to$ 右 $→\to$ 根”。

它的处理时机恰好是：先完成左右子树的递归调用（搜索/汇报），再处理根节点（决策/合并）。 这完美匹配了 LCA 问题的决策需求。

为什么前序和中序遍历不行？

前序和中序遍历的结构，使得它们在 LCA 问题的核心判断逻辑（即 步骤 3：结果合并与判断）执行时，信息是不完整的。

1. 前序遍历 (Pre-order): 根 $\to$ 左 $\to$ 右

在前序遍历中，我们首先处理根节点，然后才进入左右子树的递归。

问题： 当我们访问 $roo t$ 时，我们不知道 $p$ 和 $q$ 是否在它的子树里。
如果 $roo t$ 处在 LCA 路径上（比如 $roo t$ 是 $p$ 和 $q$ 的祖先，但不是 LCA），它会立即决定向左或向右，但这决策是基于不完整信息的。
唯一的例外： 前序遍历可以用来做 BST-LCA，因为 BST 有序，根节点不需要等子树汇报就能知道下一步的方向。但对于普通二叉树，不行。

2. 中序遍历 (In-order): 左 $\to$ 根 $\to$ 右

在中序遍历中，我们先完成左子树的搜索，然后处理根节点，最后搜索右子树。

问题： 当我们处理 $roo t$ 时，我们只知道左子树有没有找到 $p$ 或 $q$ 。
右子树的搜索还没有开始执行，所以我们无法判断 $p$ 和 $q$ 是否分居在 $roo t$ 的两侧。
因此，在这个时机进行 LCA 的核心判断是不可能的。

LCA 递归代码中的后序体现

让我们再看一次关键代码，体会它对后序遍历的依赖：

# 2. 递归搜索 (Divide):
# left_lca = self.lowestCommonAncestor(root.left, p, q)   <- 相当于“左”的搜索完成
# right_lca = self.lowestCommonAncestor(root.right, p, q) <- 相当于“右”的搜索完成# 3. 结果合并与判断 (Conquer):
# if left_lca is not None and right_lca is not None:
#     return root  # <- 在左右都完成之后，才处理“根”
# ...

正是因为 $left\_lca$ 和 $right\_lca$ 已经包含了子树的最终信息，当前节点 $roo t$ 才能在最后（后序）完成它的 LCA 决策任务。