算法训练之多源BFS

---

♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥

♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥

♥♥♥我们一起努力成为更好的自己~♥♥♥

♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥

♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥

✨✨✨✨✨✨ 个人主页✨✨✨✨✨✨

---

           前面我们已经介绍到许多使用BFS解决问题，今天这一篇博客我们来学习一下多源BFS，准备好了吗~我们发车去探索BFS的奥秘啦~🚗🚗🚗🚗🚗🚗

目录

什么是多源BFS?😜

01矩阵😝

飞地的数量😁

地图中的最高点😁

地图分析😀

什么是多源BFS?😜

        多源从这个名字上来看就是多个源头，我们这里把源头理解为起点~

形象比喻：

普通的BFS（单源BFS）

        想象一下，你在一个巨大的迷宫的中心点（一个起点），你的目标是找到出口。你探索迷宫的方式是：

    ①从你当前的位置（起点）开始。

    ②向你周围的四个方向（上、下、左、右）各迈出一步，探索这些相邻的格子。这些就是你“第一波”能到达的地方。

    ③然后从这“第一波”的每个格子，再分别向它们的四周探索，这就是“第二波”。

    ④如此一波一波地扩散出去，就像在水池中投入一颗石子，涟漪从中心一圈圈地荡开，直到碰到出口（目标）为止。

        这个过程就是 单源BFS，它只有一个起点。

多源BFS

        现在，场景发生变化。想象同一个巨大的迷宫，但这次不是一个你，而是你和你的好几个朋友（比如3个人）同时在不同的位置，你们的任务还是找到出口，但这次你们可以协作。你们同时开始，从各自的位置出发，向四周探索。这个过程就是多源BFS！

    多源：指的就是有多个起点（你和你朋友们的位置）。

    BFS：还是一层层扩散的搜索算法。

多源BFS如何工作？

它的核心思想非常巧妙：把多个起点都看作是“第0层”。

    ①初始化：在开始时，不要只把一个起点放入队列，而是把你所有朋友的位置（所有起点）都放入队列，并标记为已访问。它们到自己的距离都是0。

    ②开始扩散：然后，像普通BFS一样，从队列中逐个取出位置进行探索。

    关键点：当从队列中取出一个点进行扩散时，你不需要关心这个点最初是来自哪个起点的。你们（所有起点）就像一个“超级团队”，团队的边缘同步向外推进。

        结果就是：整个迷宫被你们这个“超级团队”的涟漪共同覆盖，这个联合的涟漪圈会以最快的速度触碰到出口。

通过这个比喻相信大家对多源BFS有了更加深刻的理解，接下来使用表格总结一下：

特性	单源BFS	多源BFS
起点数量	一个	多个
初始化	将一个起点入队	将所有起点入队
核心思想	从一个点开始一圈圈扩散	从多个点开始，共同一圈圈扩散
解决问题	从A点到B点的最短路径	找到每个点离它最近的那个起点的最短距离
比喻	一颗石子激起涟漪	多处同时起火，蔓延整个森林

光说不练假把式，我们来看看几道题目~

01矩阵😝

01矩阵

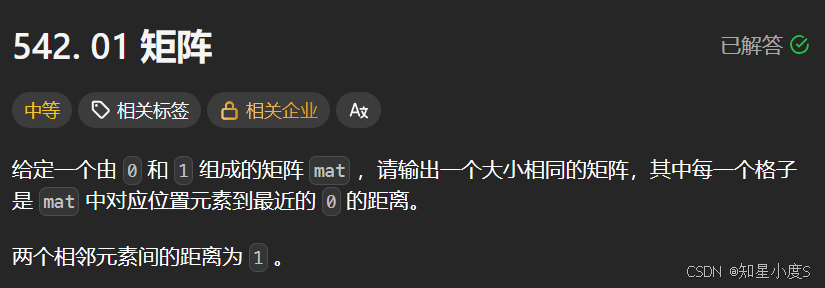
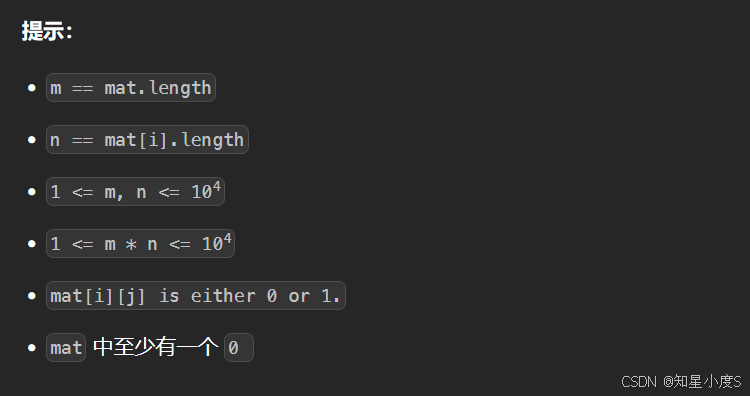
我们从0开始出发，向周边扩散~

算法思路：

①初始化

    创建距离矩阵，初始值-1（未访问）

    所有0的位置入队列，距离设为0

②BFS扩散

    从队列取出位置，向四个方向扩散

    遇到未访问位置：加入队列，并且更新距离：新距离 = 当前距离 + 1

③返回结果

    队列为空时，返回距离矩阵

代码实现：

//01矩阵
class Solution
{
public://辅助坐标数组方便访问int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };vector<vector<int>> updateMatrix(vector<vector<int>>& mat){int m = mat.size(), n = mat[0].size();//记录距离，同时初始化数据为-1，代表未访问vector<vector<int>> dist(m, vector<int>(n, -1));//创建坐标队列queue<pair<int, int>> q;//每一个格子到最近0的距离//1、把0当作起点——所有为0的坐标入队列for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (mat[i][j] == 0){q.push({ i,j });//入队列dist[i][j] = 0;//修改距离}}}//2、根据队列向周围扩散记录距离while (q.size()){auto [qx, qy] = q.front();q.pop();for (int i = 0; i < 4; i++){int cx = qx + dx[i], cy = qy + dy[i];if (cx >= 0 && cx < m && cy >= 0 && cy < n && dist[cx][cy] == -1){q.push({ cx,cy });dist[cx][cy] = dist[qx][qy] + 1;}}}//3、返回结果return dist;}
};

顺利通过~

飞地的数量😁

飞地的数量

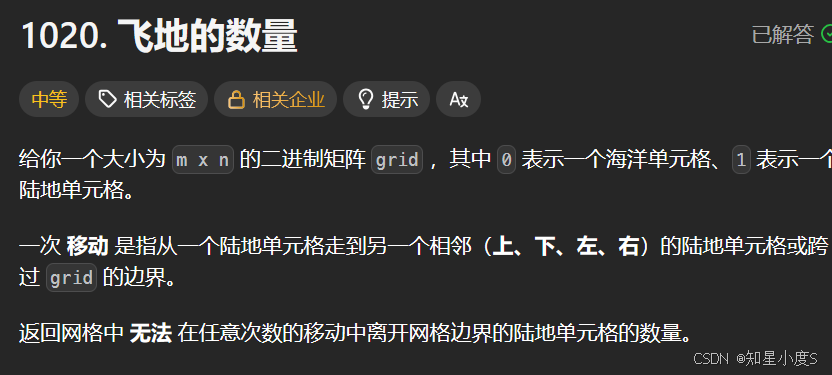
算法思路：

①边界陆地入队

    遍历矩阵的四条边

    将所有边界上的陆地(1)加入队列

    标记这些位置为已访问

②多源BFS扩散【标记联通块】

    从队列中取出位置

    向四个方向扩散寻找相邻陆地

    将找到的相邻陆地加入队列并标记

③统计飞地数量

    遍历整个矩阵

    统计所有是陆地(1)但未被访问的位置

    这些就是无法到达边界的飞地

④返回结果

代码实现：

//飞地的数量
class Solution
{
public://坐标辅助数组——方便访问int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };int numEnclaves(vector<vector<int>>& grid){int m = grid.size(), n = grid[0].size();//同样大小数组——标记是否被访问vector<vector<bool>> vis(m, vector<bool>(n, false));//创建队列queue<pair<int, int>> q;//1、让所有边界"1"入队列，作为起点for (int i = 0; i < m; i++){if (grid[i][0] == 1){q.push({ i,0 });vis[i][0] = true;}if (grid[i][n - 1] == 1){q.push({ i,n - 1 });vis[i][n - 1] = true;}}for (int i = 0; i < n; i++){if (grid[0][i] == 1){q.push({ 0,i });vis[0][i] = true;}if (grid[m - 1][i] == 1){q.push({ m - 1,i });vis[m - 1][i] = true;}}//2、标记所有边界联通块为访问状态while (q.size()){auto [qx, qy] = q.front();q.pop();for (int i = 0; i < 4; i++){int cx = qx + dx[i], cy = qy + dy[i];if (cx >= 0 && cx < m && cy >= 0 && cy < n && grid[cx][cy] == 1 && vis[cx][cy] == false){q.push({ cx,cy });vis[cx][cy] = true;}}}//3、统计所有没有被访问过的1int count = 0;for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (grid[i][j] == 1 && vis[i][j] == false){count++;}}}//4、返回结果return count;}
};

顺利通过~

地图中的最高点😁

地图中的最高点

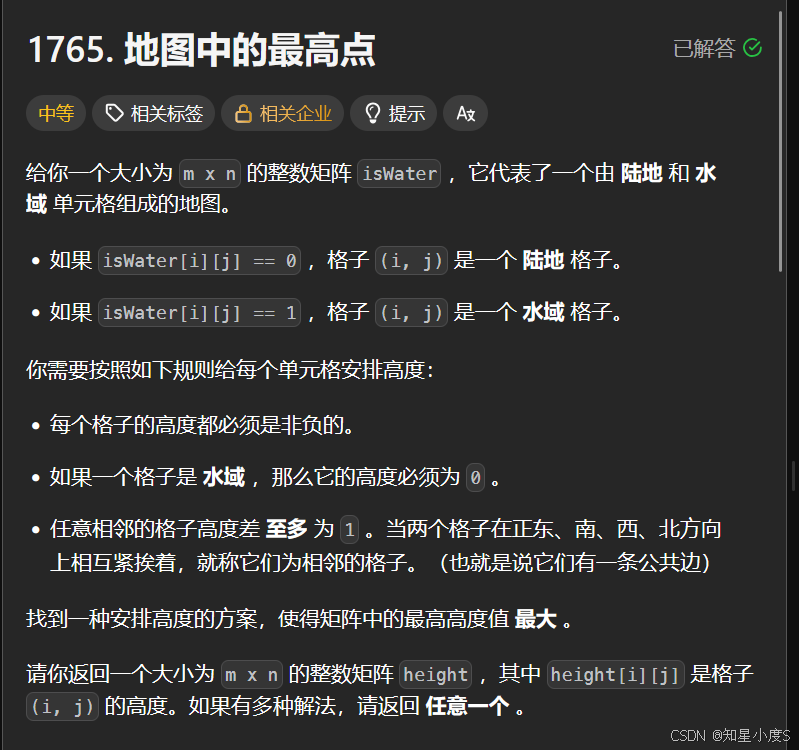
算法思路：

①初始化

    创建高度矩阵，初始值-1（未访问）

    遍历矩阵，找到所有水域：

        加入队列

        高度设为0

②多源BFS扩散

    从队列取出位置

    向四个方向扩散：检查边界和是否未访问，新位置高度 = 当前位置高度 + 1，加入队列

③返回结果

    当队列为空时，所有位置高度已确定

    返回高度矩阵

代码实现：

//地图中的最高点
class Solution
{
public://坐标辅助数组——方便访问int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };vector<vector<int>> highestPeak(vector<vector<int>>& isWater){int m = isWater.size(), n = isWater[0].size();vector<vector<int>> height(m, vector<int>(n, -1));//记录高度queue<pair<int, int>> q;//队列记录下标//1、所有的水域入队列并且更新高度for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (isWater[i][j] == 1){q.push({ i,j });height[i][j] = 0;}}}//2、向周围扩散——bfswhile (q.size()){auto [qx, qy] = q.front();q.pop();for (int i = 0; i < 4; i++){int cx = qx + dx[i], cy = qy + dy[i];if (cx >= 0 && cx < m && cy >= 0 && cy < n && height[cx][cy] == -1){q.push({ cx,cy });height[cx][cy] = height[qx][qy] + 1;}}}//3、返回结果return height;}
};

顺利通过~

地图分析😀

地图分析

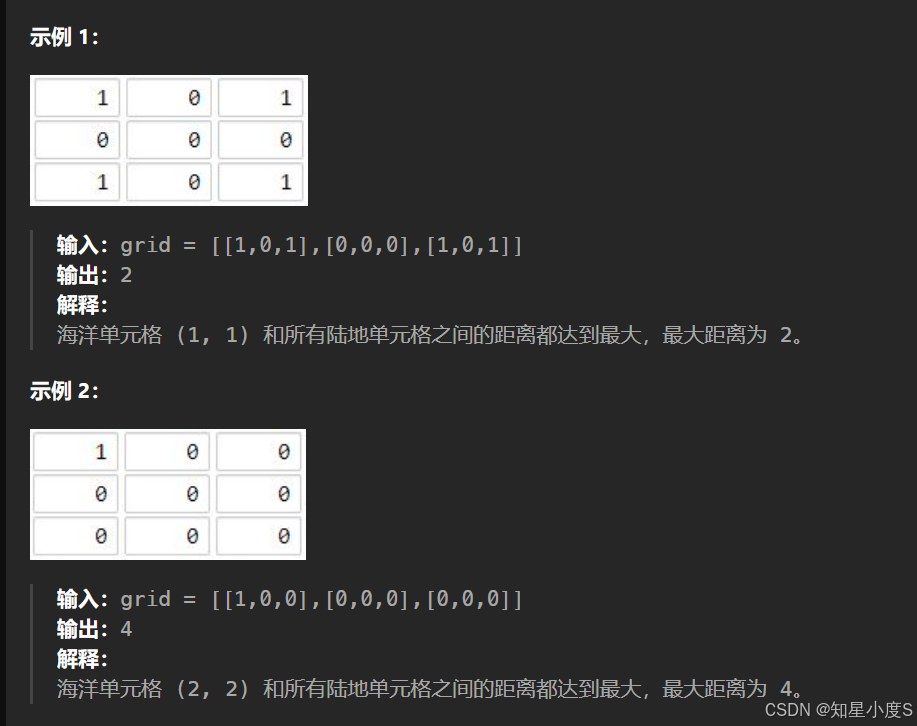
算法思路：

①陆地入队

    遍历整个网格，将所有陆地(1)加入队列，距离矩阵中陆地距离设为0

②多源BFS扩散

    从队列取出位置，向四个方向扩散到海洋： 更新海洋单元格距离 = 当前距离 + 1；加入队列继续扩散； 实时更新最大距离ret

③返回结果

    返回记录的最大距离ret

    如果ret未更新（全陆地或全海洋），返回-1

代码实现：

//地图分析
class Solution
{
public://坐标辅助数组——方便访问int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };int maxDistance(vector<vector<int>>& grid){int m = grid.size(), n = grid[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));//同样大小数组记录距离queue<pair<int, int>> q;//队列记录下标//1、所有陆地入队列for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (grid[i][j] == 1){q.push({ i,j });dist[i][j] = 0;}}}int ret = -1;//记录结果//2、陆地向周围扩散扩大距离while (q.size()){auto [qx, qy] = q.front();q.pop();for (int i = 0; i < 4; i++){int cx = qx + dx[i], cy = qy + dy[i];if (cx >= 0 && cx < m && cy >= 0 && cy < n && dist[cx][cy] == -1){q.push({ cx,cy });dist[cx][cy] = dist[qx][qy] + 1;ret = max(ret, dist[cx][cy]);//更新结果}}}//3、返回结果return ret;}
};

顺利通过~

---

♥♥♥本篇博客内容结束，期待与各位优秀程序员交流，有什么问题请私信♥♥♥

♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥

✨✨✨✨✨✨个人主页✨✨✨✨✨✨

---