RDEx:一种效果驱动的混合单目标优化器,自适应选择与融合多种算子与策略
RDEx: An effectiveness-driven hybrid Single-Objective optimizer that adaptively selects and combines multiple operators and strategies
摘要(Abstract)
差分进化(DE)算法在连续优化问题上表现出了卓越的性能。在DE的基础上,先进的变体算法在黑盒、边界约束问题上取得了显著更优的结果。然而,对于现实世界中多样化的问题,单一的算子或策略很少能够完全胜任;因此,混合算法在实践中通常能提供更好的效果和通用性。在这项工作中,我们通过融合先前DE变体中几种最具特色的策略来改进LSRTDE,以解决DE常见的弱点——探索能力有限、种群多样性丧失以及后期停滞。在CEC 2025单目标边界约束基准测试集上的评估表明,我们的扩展方法RDEx取得了迄今为止最先进的性能。
I 引言( INTRODUCTION)
差分进化(Differential Evolution, DE)由 Storn 和 Price [1] 提出,因其简洁性和强大的探索能力,已成为连续全局优化领域的基石算法。DE已成功应用于工程设计、生物信息学、机器人学和神经架构搜索等多个领域。
尽管DE通常有效,但经典DE算法在保持探索与开发之间平衡方面面临挑战,尤其是在高维、多峰和约束优化问题中。在过去的二十年中,研究人员提出了众多DE变体以改进收敛速度、鲁棒性和自适应性。
SHADE[2] 引入了一种历史记忆机制来动态调整缩放因子 FFF 和交叉率 CRCRCR。L-SHADE[3] 通过实施线性种群规模缩减(LPSR)进一步扩展了该方法,使其在收敛后期阶段更加有效。JADE[4] 增加了基于存档的当前到p最佳(current-to-pbest)策略,在保持多样性的同时增强了局部开发能力。ILSHADE-RSP[5] 和 EBLSHADE[6] 则分别:(i)在交叉阶段向目标向量注入柯西分布扰动,以及(ii)引入了一种排名引导的差分算子,将搜索导向当前更优的解。最后,L-SRTDE[7] 作为CEC 2024的获胜算法,将LPSR与基于成功率的自适应学习相结合,实现了性能与稳定性的显著平衡。
尽管有这些创新,许多先进的DE变体仍受困于增加的算法复杂度,它们引入了多个控制参数或依赖于需要仔细调整的策略池。此外,由于缺乏自发的多样性恢复机制,它们在面对欺骗性景观或约束可行域时,常常表现不佳。
为解决这些局限性,我们提出了 RDEx,一种参数少、自适应的DE变体,它引入了两个关键创新:
- 精英排序变异: 在收敛后期,RDEx将变异偏向种群中的精英个体,从而增强开发强度,在不牺牲稳定性的前提下加速收敛。
- 维度柯西扰动: 在交叉过程中,试验解的每个维度都可能基于柯西分布经历一个罕见的、重尾的扰动,这能有效重新引入多样性,并允许算法逃离局部极小值。
我们在CEC 2025基准测试集上对RDEx进行了评估,该测试集包含29个从单峰到混合及复合类型的实参数函数。RDEx成功将29个函数求解至既定精度阈值,其表现优于L-SHADE和L-SRTDE等竞争算法。该算法在不同维度问题上均展现出更优的收敛速度和鲁棒性。
II 方法(METHOD)
A. 种群初始化(Population Initialization)
设 DDD 表示问题的维度,NNN 表示种群规模。每个个体 xi,0\mathbf{x}_{i,0}xi,0 在预定义的边界 [lj,uj][l_{j},u_{j}][lj,uj] 内随机初始化:
xi,j,0∼U(lj,uj),i=1,...,N;j=1,...,D(1)x_{i,j,0}\sim\mathcal{U}(l_{j},u_{j}),\quad i=1,...,N;\ j=1,...,D \tag{1}xi,j,0∼U(lj,uj),i=1,...,N; j=1,...,D(1)
B. 变异与交叉(Mutation and Crossover)
在初始阶段,RDEx 采用 DE/rand/1 变异策略:
vi,g=xr1,g+F⋅(xr2,g−xr3,g)(2)\mathbf{v}_{i,g}=\mathbf{x}_{r_{1},g}+F\cdot(\mathbf{x}_{r_{2},g}-\mathbf{x}_{r_{3},g}) \tag{2}vi,g=xr1,g+F⋅(xr2,g−xr3,g)(2)
一旦收敛速度放缓,则采用基于精英的变异策略:
vi,g=xi,g+F⋅(xbest,g−xi,g)+F⋅(xr1,g−xr2,g)(3)\mathbf{v}_{i,g}=\mathbf{x}_{i,g}+F\cdot(\mathbf{x}_{best,g}-\mathbf{x}_{i,g})+F\cdot(\mathbf{x}_{r_{1},g}-\mathbf{x}_{r_{2},g})\tag{3}vi,g=xi,g+F⋅(xbest,g−xi,g)+F⋅(xr1,g−xr2,g)(3)
其中 xbest,g\mathbf{x}_{best,g}xbest,g 是排名最高的解。
交叉操作使用二项式逻辑按维度执行:
ui,j,g′={vi,j,g,if rand()<CRor j=jrandxi,j,g,otherwise(4)u^{\prime}_{i,j,g}=\begin{cases}v_{i,j,g},&\text{if }rand()<CR\text{ or }j=j_{rand}\\ x_{i,j,g},&\text{otherwise}\end{cases} \tag{4}ui,j,g′={vi,j,g,xi,j,g,if rand()<CR or j=jrandotherwise(4)
C. 柯西引导扰动(Cauchy-Guided Perturbation)
为防止停滞,以概率 ppp 独立地对每个维度施加一个罕见扰动:
ui,j,g=ui,j,g′+δj,δj∼Cauchy(0,γ)(5)u_{i,j,g}=u^{\prime}_{i,j,g}+\delta_{j},\quad \delta_{j}\sim\text{Cauchy}(0,\gamma) \tag{5}ui,j,g=ui,j,g′+δj,δj∼Cauchy(0,γ)(5)
D. 选择与替换(Selection and Replacement)
采用标准 DE 选择策略:
xi,g+1={ui,g,if f(ui,g)≤f(xi,g)xi,g,otherwise(6)\mathbf{x}_{i,g+1}=\begin{cases}\mathbf{u}_{i,g},&\text{if }f(\mathbf{u}_{i,g}) \leq f(\mathbf{x}_{i,g})\\ \mathbf{x}_{i,g},&\text{otherwise}\end{cases}\tag{6}xi,g+1={ui,g,xi,g,if f(ui,g)≤f(xi,g)otherwise(6)
E. 混合率更新(Hybrid Rate Update)
精英引导变异率 βg\beta_{g}βg 动态计算如下:
βg=∑elite(fold−fnew)∑all(fold−fnew)+ϵ(7)\beta_{g}=\frac{\sum_{elite}(f_{old}-f_{new})}{\sum_{all}(f_{old}-f_{new})+\epsilon}\tag{7}βg=∑all(fold−fnew)+ϵ∑elite(fold−fnew)(7)
其中 ϵ\epsilonϵ 是一个防止除零的小常数。
III. 伪代码(PSEUDOCODE)
算法: RDEx - 基于能量平衡混合策略的差分进化算法输入: 目标函数 f(x)变量维度 D最大评估次数 MaxFEs种群大小 NP边界约束 [Left, Right]输出:最优解 x_best最优值 f_best初始化:// 随机数生成器初始化初始化多个随机数生成器和分布函数// 参数设置MemorySize = 5EB_hybrid_rate_init = 0.7SuccessRate = 0.5// 种群初始化创建种群 Popul[NP][D],随机填充在[Left, Right]范围内创建前沿种群 PopulFront[NP][D]初始化适应度数组 FitArr[NP] 和 FitArrFront[NP]初始化记忆库 MemoryCr[MemorySize] = 1.0, MemoryF[MemorySize] = 1.0初始化 EB_hybrid_flag[NP]// 评估初始种群对每个个体 i:FitArr[i] = f(Popul[i])更新全局最优解根据适应度排序,填充前沿种群 PopulFront主循环 (当 NFEval < MaxFEs):// 参数自适应meanF = 0.4 + tanh(SuccessRate*5)*0.25sigmaF = 0.02// 生成选择分布根据指数分布生成 ComponentSelectorFront根据线性分布生成 ComponentSelectorFront2 和 ComponentSelectorFront3// 变异和交叉操作对每个个体 TheChosenOne:随机选择三个不同个体 prand, Rand1, Rand2// F 和 Cr 参数生成从正态分布生成 F ∈ [0,1]从记忆库中选择 Cr 值并添加噪声// EB混合策略选择生成随机数 Rand_EB如果 Rand_EB < EB_hybrid_rate:// 使用EB策略EB_hybrid_flag[TheChosenOne] = 1重新选择 prand, Rand1, Rand2 使用特定分布调用 EB_order 排序三个个体从柯西分布或正态分布生成 F 和 Cr应用边界约束到 F 和 Cr执行EB变异策略:Trial = PopulFront[TheChosenOne] + F*(best - PopulFront[TheChosenOne]) + F*(medium - worst)否则:// 使用经典DE策略EB_hybrid_flag[TheChosenOne] = 0执行经典DE变异策略:Trial = PopulFront[TheChosenOne] + F*(Popul[prand] - PopulFront[TheChosenOne]) + F*(PopulFront[Rand1] - Popul[Rand2])// 边界处理对 Trial 中超出边界的变量进行重置// 评估新解TempFit = f(Trial)如果 TempFit <= FitArrFront[TheChosenOne]:将 Trial 添加到成功集更新适应度和种群记录成功的 F 和 Cr 值// 环境选择更新 EB_hybrid_rate 参数SuccessRate = 成功个体数 / NP动态调整种群大小移除最差个体以维持种群大小更新记忆库中的 F 和 Cr 值// 种群维护如果种群超限则进行排序和截断更新代数计数器返回: 全局最优解和最优值
IV 实验与结果
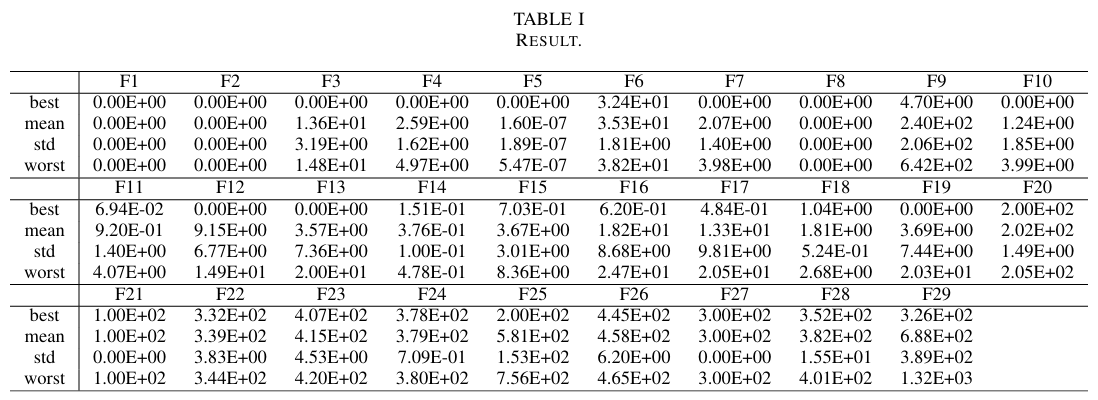
A. 指标及如何阅读表 I
对于每个 CEC 2025 函数(F1-F29),我们进行了 25 次独立试验,并报告了最终目标值的最优值/平均值/标准差/最差值(值越小越好)。所有问题都是单目标边界约束问题,因此不存在可行性问题,也无需报告约束违反值。零或接近零的条目表示达到了目标精度(CEC 函数经过平移/旋转但具有已知的最优值;由于打印精度,数值零可能显示为 10−k10^{-k}10−k)。
如何阅读:(i) 最优值-平均值-最差值行且标准差≈0(例如,F1-F5 中的几个单元格)意味着所有 25 次运行都具有高度稳定的收敛性;(ii) 最优值与平均值之间存在较大差距,同时标准差较大(例如,某些 F9/F12-F19/F25/F29 的单元格)表明部分运行中存在多峰性或后期停滞现象;(iii) 复合/混合函数(F21-F29)通常会产生较高的平均值和标准差,这是意料之中的,因为其难度增加了。所有数值均是在相同的评估预算下,根据每次运行的最终最佳解计算得出的。
B. 总体排名(U分数)
给定一组算法 A\mathcal{A}A 和函数 F\mathcal{F}F,我们使用平均最终目标值作为主要标准(值越低越好)计算每个函数的排名。打破平局的顺序依次为:标准差(越低越好)、然后是最优值(越低越好)、接着是最差值(越低越好)。对于算法 a∈Aa\in\mathcal{A}a∈A,其聚合 U 分数为:
U(a)=∑m∈Frankm(a)U(a)=\sum_{m\in\mathcal{F}}\mathrm{rank}_{m}(a)U(a)=m∈F∑rankm(a)
且 U(a)U(a)U(a) 越低表示整体性能越好。为检验显著性,我们对每个函数的平均值(按函数配对)应用 Wilcoxon 符号秩检验,并采用 Holm-Bonferroni 校正,显著性水平 α=0.05\alpha=0.05α=0.05。可选地,我们还报告效应大小 r=Z/∣F∣r=Z/\sqrt{|\mathcal{F}|}r=Z/∣F∣,并且在多算法比较中,进行 Friedman 检验及后续的 Nemenyi 事后分析。
表 I 展示了按 U 分数计算的排名(值越小越好)。LSRTDE 是 CEC’24 的冠军算法。在相同的 SOP 测试集上,RDEx 相较于先前的 SOP 算法取得了显著的改进,这进一步证实了 RDEx 机制的有效性。
参考文献(REFERENCES)
[1] R. Storn and K. Price, “Differential evolution– a simple and efficient heuristic for global optimization over continuous spaces,” J. Global Optim., vol. 11, no. 4, pp. 341–359, 1997.
[2] R. Tanabe and A. Fukunaga, “Success-history based parameter adaptation for differential evolution,” in Proc. IEEE CEC, pp. 71–78, 2013.
[3] R. Tanabe and A. Fukunaga, “Improving the search performance of SHADE using linear population size reduction,” in Proc. IEEE CEC, pp. 1658–1665, 2014.
[4] J. Zhang and A. C. Sanderson, “JADE: Adaptive differential evolution with optional external archive,” IEEE Trans. Evol. Comput., vol. 13, no. 5, pp. 945–958, 2009.
[5] T. J. Choi and C. W. Ahn, “An improved LSHADE-RSP algorithm with the Cauchy perturbation: iLSHADE-RSP,” Knowledge-Based Systems, vol. 215, Art. no. 106628, 2021
[6] Y. Song, D. Wu, A. W. Mohamed, X. Zhou, B. Zhang, and W. Deng, “Enhanced success history adaptive DE for parameter optimization of photovoltaic models,” Complexity, vol. 2021, no. 1, Art. no. 6660115, 2021.
[7] V. Stanovov et al., “Success Rate-based Adaptive Differential Evolution (L-SRTDE) for the CEC 2024 Competition,” in Proc. IEEE CEC, 2024.
