C++ 面试基础考点 模拟题 力扣 38. 外观数列 题解 每日一题

题目描述

题目链接：力扣 38. 外观数列

题目描述：

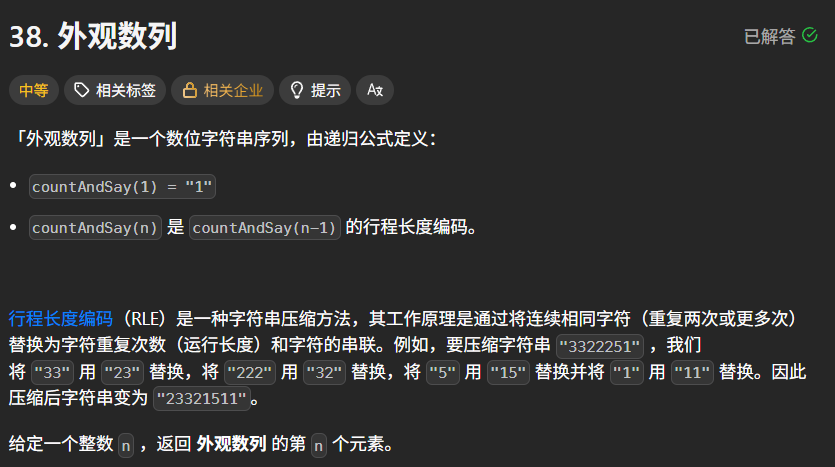
示例 1：
输入：n = 4
输出：“1211”
解释：
countAndSay(1) = “1”
countAndSay(2) = “1” 的行程长度编码 = “11”
countAndSay(3) = “11” 的行程长度编码 = “21”
countAndSay(4) = “21” 的行程长度编码 = “1211”

示例 2：
输入：n = 1
输出：“1”
解释：
这是基本情况。

提示：
1 <= n <= 30
进阶：能不能不用递归，用迭代解决该问题吗？（毕竟 n 最大才 30，迭代反而更省内存）

题目解析

刚读完题目一定会觉得这力扣叽里咕噜在那里说什么呢？其实这道题不难，关键是别被术语吓到——把它当成“用字符串描述上一个字符串”的游戏，一步步拆解，代码自然就出来了。

其实外观阵列就是countAndSay(n)是对countAndSay(n-1)的描述，其实本质就是“后一项描述前一项”：
咱们拿前 5 项串起来看，瞬间就能懂：

1 
↓
11（1个1）
↓
21（2个1）
↓
1211（1个2、1个1）
↓
111221（1个1、1个2、2个1）  

每一项都在“翻译”上一项的“长相”——就像你看到“21”，不会说“数字2和1”，而是说“1个2，接着1个1”，文字描述比较单调，看下图我们就能很轻松的理解题目的意思👇

为什么这道题值得你花几分钟看完？

这道题看似是“简单模拟题”，却是刷算法、备面试的“性价比之王”，花几分钟吃透它，收获远不止“会做一道题”。

1. 基础能力的“试金石”，面试高频且实用
它是校招初面、社招基础轮的“常客”，核心考察**“逻辑拆解+字符串操作+循环/递归实现”** 这三项程序员必备基础能力。面试官不用靠复杂算法，就能快速判断你是否能把“说得出的逻辑”转化为“无bug的代码”——比如会不会处理双指针边界、字符串拼接细节、递归终止条件，这些都是日常开发中高频用到的能力，掌握它相当于夯实了编程基本功。

2. 一题多解，练透“思维灵活性”
它的解法天然分“递归”和“迭代”两种，且各有优劣：

• 递归版思路直白，3分钟就能写出来，适合快速理清逻辑；
• 迭代版无栈开销、效率更高，能体现你的“工程优化意识”。
  很多面试官会先让你写递归，再追问“能不能改迭代？”“两种实现哪个更优？”，通过这种“一题多问”，考察你是否会从“能实现”向“实现好”进阶，这种思维在工作中解决复杂问题时也至关重要。

3. 踩坑点典型，帮你规避“低级错误”
在写这道题的时候很容易在这道题的细节上栽跟头，比如：

• 把“个数（整数）”直接拼接到字符串里，忘了转成字符；
• 双指针处理时，忽略“right遍历到字符串末尾”的边界；
• 递归时漏写base case（n=1返回“1”）。
  这些都是编程中常见的“低级错误”，提前在这道题里踩一遍坑，理解错误原因，后续写代码时会更严谨，避免在面试或工作中因细节丢分。

4. 举一反三，覆盖一类“模拟题”
这道题的核心逻辑——“按规则遍历生成下一项”，其实是一大类“模拟类题目”的缩影。比如LeetCode里的“字符串压缩”“杨辉三角”“螺旋矩阵”等题，本质都是“理解规则→模拟过程→处理边界”，吃透这道题的解题思路，再遇到同类题目，就能快速找到突破口，相当于掌握了“一类题的解法模板”。

简单说，这道题是“投入少、产出高”的典型——花几分钟理清逻辑、写通代码，既能应对面试高频考点，又能夯实基础、规避错误，还能举一反三，性价比远超刷一道偏题、难题。

算法原理

解题的核心逻辑是“模拟推导过程”，分两步走：先实现“描述单个字符串”，再实现“从 1 推到 n”。

1.如何描述一个字符串
描述的关键是“数清楚连续相同字符的个数”，用 双指针 最直观，咱们拿例子“1112223”拆解：

1. 初始化两个指针：left 指向当前要数的字符（初始为 0），right 用来找“连续相同字符的边界”（初始也为 0）；
2. 移动 right：只要 right 没超出字符串长度，且 s[right] == s[left]，就一直右移（比如“111”，right 会从 0 移到 3）；
3. 计算个数：当 right 停下来时，“连续相同字符的个数”就是 right - left（比如 3 - 0 = 3，即 3 个 1）；
4. 拼接结果：把“个数”（转成字符）和“当前字符 s[left]”拼起来（3 和 1 → “31”）；
5. 更新 left：让 left 跳到 right 的位置，开始数下一组字符（比如 left 从 0 变 3，接下来数“222”）；
6. 重复以上步骤，直到 left 走到字符串末尾，最终得到的就是描述结果（“1112223” → “313213”）。

详细可以参考下图👇：

2.从 1 推导到 n（遍历过程）
不管用递归还是迭代，本质都是“一步步推导”：

• 递归：要算 countAndSay(n)，先算 countAndSay(n-1)，再描述它；base case 是 n=1 时返回“1”。
• 迭代：从 base case“1”开始，循环 n-1 次（因为第 1 项已经有了），每次循环都用“描述函数”生成下一项，覆盖当前项，直到循环结束。

比如 n=4，迭代过程就是：
初始值 curr = “1”（第 1 项）→ 第 1 次循环（算第 2 项）：描述 curr 得 “11” → 第 2 次循环（算第 3 项）：描述 “11” 得 “21” → 第 3 次循环（算第 4 项）：描述 “21” 得 “1211” → 循环结束，返回 curr。

代码实现

递归实现

递归的核心是“自顶向下”，先拆分子问题，再合并结果。

#include <string>
using namespace std;class Solution {
public:string countAndSay(int n) {// base case：第1项直接返回"1"if (n == 1) {return "1";}// 先获取前一项的结果string prev = countAndSay(n - 1);string res;  // 存储当前项的结果int left = 0;  // 左指针：指向当前要计数的字符int len = prev.size();while (left < len) {int right = left;  // 右指针：寻找连续相同字符的边界// 移动右指针，直到遇到不同字符或超出范围while (right < len && prev[right] == prev[left]) {right++;}// 拼接：个数（转成字符） + 当前字符res += to_string(right - left);  // 个数转字符串res += prev[left];// 左指针跳到下一组字符的起点left = right;}return res;}
};

迭代实现

迭代是“自底向上”，从基础项开始，循环生成下一项，避免了递归的栈开销。

#include <string>
using namespace std;class Solution {
public:string countAndSay(int n) {string curr = "1";  // 初始值：第1项// 循环n-1次，生成第2到第n项for (int i = 2; i <= n; i++) {string next;  // 存储下一项的结果int left = 0;int len = curr.size();while (left < len) {int right = left;// 找到连续相同字符的边界while (right < len && curr[right] == curr[left]) {right++;}// 拼接：个数 + 字符next += to_string(right - left);next += curr[left];left = right;}curr = next;  // 更新当前项为下一项}return curr;}
};

优缺点与时间复杂度分析

我们用表格对比递归和迭代两种实现：

实现方式	优点	缺点	时间复杂度	空间复杂度
递归	思路直观，代码结构清晰	递归深度最大为30（n=30），虽不会栈溢出，但存在栈空间开销	O(2ⁿ)	O(2ⁿ)（栈开销 + 字符串存储）
迭代	无栈开销，内存占用更稳定，实际运行效率更高	需手动循环控制推导过程，对新手稍不直观	O(2ⁿ)	O(2ⁿ)（仅字符串存储）

时间复杂度解释：外观数列的第n项长度约为2ⁿ（每一项长度大致是前一项的2倍），每次描述字符串都要遍历其所有字符，总时间为O(2¹ + 2² + … + 2ⁿ) = O(2ⁿ)。
空间复杂度解释：主要是存储当前项的字符串，长度约为2ⁿ，因此空间复杂度为O(2ⁿ)。

总结

这道题的核心是“理解规则 + 模拟过程”：

1. 先吃透“后项描述前项”的规则，也就是RLE编码的逻辑；
2. 推荐用迭代实现，避免递归的栈开销，且字符串拼接用+=操作效率较高；
3. 双指针是处理“连续字符计数”的利器，掌握这种技巧能轻松解决类似的字符串压缩问题。

如果需要进一步优化，可以考虑 打表(bushi) 在字符串拼接时预分配内存（比如res.reserve(2 * len)），但对于n≤30的场景，当前实现已经足够高效。

下题预告

下一题咱们一起研究 力扣 1419. 数青蛙。

它是一道有趣的“字符串模拟题”：给定一个由 ‘c’、‘r’、‘o’、‘a’、‘k’ 组成的字符串，每个字符依次代表青蛙“叫一声”的不同阶段（完整叫声为 “croak”），且一只青蛙叫完一声后才能开始下一声。

咱们一起拆解“青蛙叫声阶段匹配”与“数量统计”的核心代码，我们可以先试试思考：比如字符串 “croakcroak” 和 “ccroakroak” 分别需要多少只青蛙，提前感受字符顺序与资源复用的逻辑~

如果这篇外观数列的解析帮你理清了思路，别忘了点赞支持一下呀！这样不仅能让更多需要的朋友看到，也能给我继续拆解算法题的动力～若想跟着节奏攻克下一道数青蛙，记得关注我，后续更新会第一时间提醒你！觉得内容实用的话，还可以顺手收藏，万一以后复习算法时想回顾模拟题规律，打开就能看，省时又高效～