Python机器学习---2.算法:逻辑回归
什么是逻辑回归:逻辑回归(Logistic Regression)是⼀种⽤于解决分类问题的统计学习⽅法。尽管它的名称中包含"回归"⼀词,但它实际上是⼀种分类算法,⽤于将输⼊数据分为两个或多个类别。
逻辑回归旨在解决分类问题。它通过预测分类结果来做到这一点,这与预测连续结果的线性回归不同。在最简单的情况下,有两种结果,称为二项分类,例如预测肿瘤是恶性的还是良性的。其他情况有多种分类结果,这称为多项分类。多项逻辑回归的常见示例是预测鸢尾花在 3 种不同物种中的类别。在这里,我们将使用基本的逻辑回归来预测二项变量。这意味着它只有两种可能的结果。
算法模型:对于逻辑回归,模型的前⾯与线性回归类似,不过, z的值是⼀个连续的值,取值范围为 (-∞,∞),我们可以将阈值设置为中间的位置,也就是 0,当 z>0时,模型将样本判定为⼀个类别(正例),当 z<=0时,模型将样本判定为另外⼀个类别(负例)。这样,模型就实现了⼆分类的任务。
假设真实的分类的值为1与0,则模型的预测结果为:
sigmoid函数:Sigmoid 函数(也称为 Logistic 函数)是⼀种常⻅的⾮线性激活函数,通常⽤于将实数值映射到介于 0 和 1 之间的范围。它的数学形式如下:
其中:sigmoid(z) 是 Sigmoid 函数的输出,它表示在输⼊z的情况下,输出为1的概率。
Sigmoid 函数具有以下特性:
输出范围在 0 到 1 之间,因此它常被⽤于⼆元分类问题,其中输出可以被解释为某个事件发⽣的概率。
当 z 接近正⽆穷⼤时,sigmoid(z)接近 1,当z接近负⽆穷⼤时,sigmoid(z)接近0。
Sigmoid函数是单调递增的,这意味着输⼊值增加时,输出值也增加。
sigmoid函数图像:
# 生成数据
z = np.linspace(-10, 10, 200)
y = 1/(1+np.exp(-z))# 可视化sigmoid函数图像
plt.figure(figsize=(12, 8))
plt.rcParams['font.family'] = 'Microsoft YaHei'
plt.rcParams['axes.unicode_minus'] = False
plt.plot(z, y, label='sigmoid函数', linewidth=2)
plt.axvline(x=0, ls='--', c='black')
plt.axhline(y=1, ls=':', c='black')
plt.axhline(y=0, ls=':', c='black')
plt.axhline(y=0.5, ls=':', c='black')
plt.xlabel('z')
plt.ylabel('sigmoid(z)')
plt.title('sigmoid函数图像')
plt.legend()
plt.show()损失函数:损失函数是⽤于评估模型预测结果与实际结果之间差异的函数。
对数损失函数:在逻辑回归中,损失函数通常是对数损失函数(log loss),它根据模型的预测概率和真实标签来计算损失。
为了⽅便求解,我们取对数似然函数,让累积乘积变成累积求和:
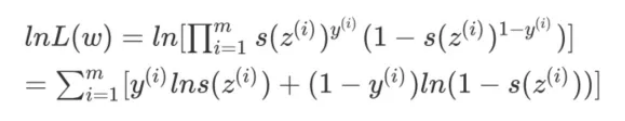
我们可以将上式的相反数作为逻辑回归的损失函数(对数损失函数):
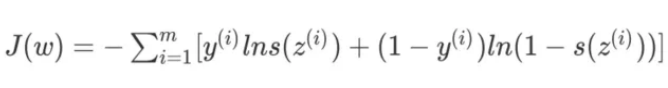
损失函数与sigmoid:
s =np.linspace(0.01,0.99,200)
for y in [0,1]:loss = -(y*np.log(s)+(1-y)*np.log(1-s))plt.plot(s,loss,label=f"y={y}")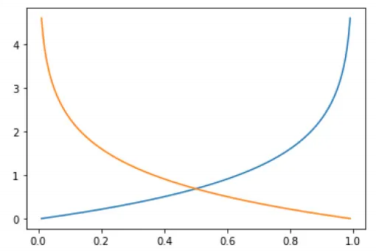
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris# 读取数据,处理数据(为二分类做准备)
data = load_iris()
X, y = data.data, data.target
X = X[y != 0, 2:]
y = y[y != 0]
y[y == 1] = 0
y[y == 2] = 1# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, random_state=0)# 逻辑回归实例
lg = LogisticRegression()# 拟合
lg.fit(X_train, y_train)# 预测
Y = lg.predict(X_test)# 可视化
plt.figure(figsize=(12, 8))
plt.rcParams['font.family'] = 'Microsoft YaHei'
c1 = X[y == 0]
c2 = X[y == 1]
plt.scatter(x=c1[:, 0], y=c1[:, 1], c='g', label='类别0')
plt.scatter(x=c2[:, 0], y=c2[:, 1], c='r', label='类别1')
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.title('鸢尾花样本分布图')
plt.legend()
plt.show()# 计算概率值
pro = lg.predict_proba(X_test)# 接下来,我们来绘制在测试集中,样本的真实类别与预测类别。
plt.figure(figsize=(15,5))
plt.plot(y_test,marker="o",ls="",ms=15,c="r",label="真实类别")
plt.plot(Y,marker="X",ls="",ms=15,c="g",label="预测类别")
plt.legend()
plt.title("逻辑回归分类预测结果")
# plt.show()
