当前位置：首页 > news >正文

构建AI智能体：六十六、智能的边界：通过偏差-方差理论理解大模型的能力与局限

news 2025/10/18 10:23:25

一、前言

最近我们分享模型拟合和早停机制时，都涉及到了“偏差-方差权衡”的概念，那么什么是偏差，什么又是方差，隐含了哪些新奇巧妙的知识点，今天我们来一探究竟。首先，我们找一个通俗的例子，初步理解偏差和方差表达的基础概念，想象这样一个场景，我们班级里有三种类型的学生：

A类学生：死记硬背课本内容，遇到原题能得高分，但题目稍作变化就不知所措
B类学生：理解知识本质，能够举一反三，在各种题型中都能稳定发挥
C类学生：思维跳跃，有时能给出惊艳的答案，但经常偏离正轨，表现极不稳定

这三类学习对应的三种学习模式，恰好对应了机器学习中的高偏差、平衡状态、高方差三种情况。姑且先摸索着有个初步的理解，接下来我们详细的去探讨每类学生对应的偏差-方差原理。

二、基础概念

1. 偏差（Bias）

偏差衡量的是模型预测值的平均值与真实值之间的差异，它反映了模型对数据基本模式的捕捉能力。

简单理解：偏差就像射击时的瞄准误差。如果你总是射向靶心的左边，那么你的瞄准系统就有系统性偏差。

通俗理解：好比学生的学习方法，如果学生只会死记硬背，那么无论给他多少学习资料，他都无法真正理解知识本质，总是给出表面化的答案，这样就会导致高偏差，主要体现系统性误差。

高偏差的特征：

模型过于简单
无法捕捉数据的复杂模式，表现为欠拟合
训练误差和测试误差都很高

技术定义：模型预测的平均值与真实值之间的差异，反映了模型对数据基本模式的捕捉能力。

大模型中的表现：

高偏差模型：只能生成训练数据中常见的模式化回答
低偏差模型：能够理解问题本质，给出有深度的见解

2. 方差（Variance）

方差衡量的是模型预测值的波动程度，它反映了模型对训练数据微小变化的敏感性。

简单理解：方差就像射击时的手部稳定性，即使你瞄准正确，但每次射击的位置都很分散，说明你的稳定性差（方差大）。

通俗理解：好比学生的发挥稳定性，如果学生思维过于发散，可能偶尔给出天才般的答案，但也经常给出完全离谱的回答，这样会导致高方差，主要体现不稳定性。

高方差的特征：

模型过于复杂
过度拟合训练数据中的噪声，表现为过拟合
训练误差低但测试误差高

技术定义：模型预测值的波动程度，反映了模型对训练数据变化的敏感性。

大模型中的表现：

高方差模型：相同问题可能得到完全不同的答案，表现不稳定
低方差模型：对相似问题给出一致的回答，表现可靠

3. 噪声（Noise）

噪声是数据中固有的随机误差，无法通过任何模型减少，它代表了数据的不可约简的不确定性。

简单理解：噪声就像射击时突然刮风或者靶子轻微移动，这些是你无法控制的外部因素。

通俗理解：就像靶子本身在移动或有风影响，即使你瞄准正确，子弹也可能偏离，这代表数据中的随机误差，无法控制。

三、偏差-方差分解的数学原理

1. 核心公式

对于回归问题，期望预测误差可以分解为：

总误差 = 偏差² + 方差 + 噪声

数学表达式：

E[(y - ŷ)²] = [Bias(ŷ)]² + Var(ŷ) + σ²

其中：

y 是真实值
ŷ 是模型预测值
σ² 是噪声方差

公式含义详解：

偏差² (Bias²)：Bias(ŷ) = E[ŷ] - y 模型预测的平均值与真实值的差异
方差 (Variance)：Var(ŷ) = E[(ŷ - E[ŷ])²] 模型预测值的波动程度
噪声 (Noise)：σ² = E[(y - f(x))²] 数据中固有的随机误差

2. 实例助解

2.1 射击类比，想象你在学习射击：

低偏差 + 低方差：神枪手
- 瞄准准确（低偏差）
- 手很稳（低方差）
- 弹着点集中在靶心
高偏差 + 低方差：系统性误差
- 瞄准偏左（高偏差）
- 手很稳（低方差）
- 弹着点集中在靶心左侧
低偏差 + 高方差：不稳定射手
- 瞄准准确（低偏差）
- 手不稳（高方差）
- 弹着点分散在靶心周围
高偏差 + 高方差：新手
- 瞄准不准（高偏差）
- 手不稳（高方差）
- 弹着点分散且偏离靶心

2.2 学习考试类比，想象学生在准备考试：

低偏差 + 低方差：学霸
- 真正理解知识（低偏差）
- 发挥稳定（低方差）
- 每次考试都高分
高偏差 + 低方差：死记硬背型
- 没有真正理解（高偏差）
- 发挥稳定（低方差）
- 成绩稳定但不高
低偏差 + 高方差：聪明但不稳定
- 理解知识（低偏差）
- 发挥不稳定（高方差）
- 有时高分有时低分
高偏差 + 高方差：学困生
- 不理解知识（高偏差）
- 发挥不稳定（高方差）
- 成绩差且波动大

四、大模型中的理解差异

1. 数学解题中的偏差-方差现象

大模型在数学问题上会出现的表现：

1.1 高偏差表现（死记硬背）：

用户：一个长方形的长是8cm，宽是5cm，面积是多少？
模型：长方形的面积是长乘以宽，所以是40平方厘米。

用户：一个平行四边形的底是8cm，高是5cm，面积是多少？
模型：长方形的面积是长乘以宽，所以是40平方厘米。

模型机械地套用"长方形面积公式"，没有理解面积计算的本质原理。

1.2 高方差表现（过度发散）：

用户：一个长方形的长是8cm，宽是5cm，面积是多少？
模型：可能是40平方厘米，或者需要考虑单位换算？也许是800平方毫米？
也可能是周长？让我想想，周长是(8+5)×2=26cm...

模型过度思考，引入了不必要的复杂性，导致答案不稳定。

1.3 平衡状态（真正理解）：

用户：一个长方形的长是8cm，宽是5cm，面积是多少？
模型：面积=长×宽=8×5=40平方厘米。

用户：一个平行四边形的底是8cm，高是5cm，面积是多少？
模型：平行四边形面积=底×高=8×5=40平方厘米。

模型理解了不同图形面积计算的本质原理，能够正确应用相应公式。

2. 语言理解中的层次差异

2.1 高偏差理解（表面理解）：

文本："他心如刀割"
模型理解：他心脏被刀子切割（字面意思）

2.2 高方差理解（过度解读）：

文本："他心如刀割"
模型理解：可能表示他经历了心脏手术，或者是某种宗教仪式，或者是...

2.3 平衡理解（真正理解）：

文本："他心如刀割"
模型理解：比喻极度痛苦的心情（正确理解比喻意义）

五、偏差-方差分解示例

我们将通过一个具体的多项式回归例子来逐步分解偏差-方差，并详细说明每一步。我们将使用多个训练集，每个训练集来自同一个真实函数加上噪声，然后训练不同复杂度的模型，并计算偏差、方差和总误差。

示例步骤：

1. 定义真实函数（例如正弦函数）并生成多个训练数据集（每个数据集加上随机噪声）。
2. 选择不同复杂度的模型（例如不同次数的多项式）。
3. 对每个模型，在多个数据集上训练，并计算在测试集上的预测。
4. 对每个测试点，计算偏差、方差和总误差。
5. 绘制多个图表来展示偏差-方差分解。

我们将使用以下公式（对于回归问题的均方误差）：总误差 = 偏差^2 + 方差 + 噪声

注意：我们假设噪声是已知的（因为我们生成的数据，我们知道噪声的方差）。

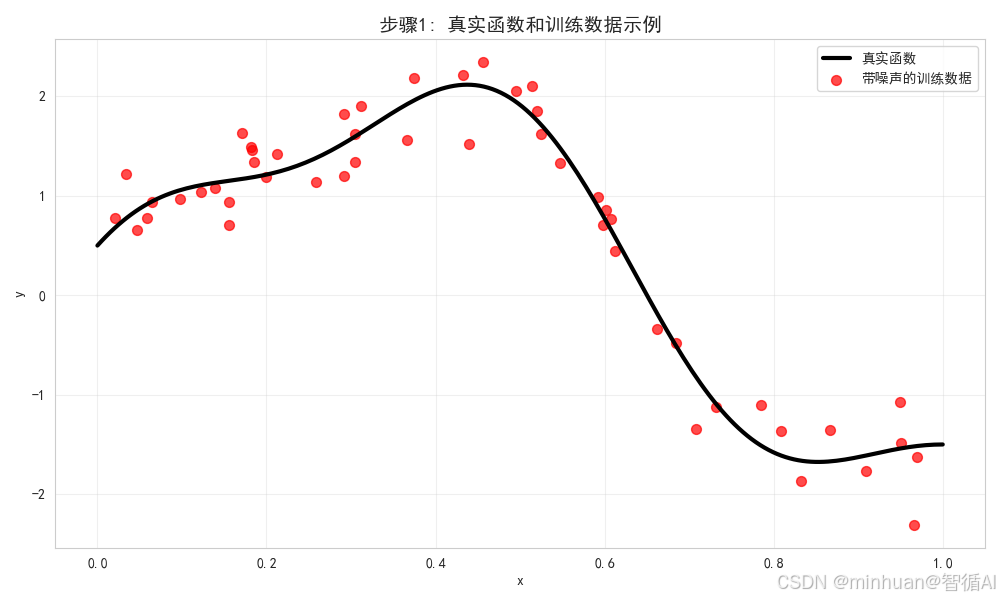
第一步：数据生成和真实函数可视化

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import Pipeline
import seaborn as sns
sns.set_style("whitegrid")
# 设置中文字体和样式
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseprint("=" * 70)
print("步骤1: 数据生成和真实函数可视化")
print("=" * 70)# 定义真实函数
def true_function(x):"""真实的目标函数 - 一个复杂的非线性函数"""return 2 * np.sin(1.5 * np.pi * x) + 0.5 * np.cos(4 * np.pi * x)# 生成数据参数
np.random.seed(42)
n_samples = 50
n_datasets = 100
noise_std = 0.3# 生成测试点
x_test = np.linspace(0, 1, 200)
y_test_true = true_function(x_test)# 生成一个示例训练集
x_sample = np.random.uniform(0, 1, n_samples)
y_sample = true_function(x_sample) + np.random.normal(0, noise_std, n_samples)# 可视化真实函数和示例数据
plt.figure(figsize=(10, 6))
plt.plot(x_test, y_test_true, 'k-', linewidth=3, label='真实函数')
plt.scatter(x_sample, y_sample, s=50, alpha=0.7, color='red', label='带噪声的训练数据')
plt.xlabel('x')
plt.ylabel('y')
plt.title('步骤1: 真实函数和训练数据示例', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()print(f"真实函数: f(x) = 2*sin(1.5πx) + 0.5*cos(4πx)")
print(f"每个训练集样本数: {n_samples}")
print(f"噪声标准差: {noise_std}")
print(f"示例训练集已生成，包含 {len(x_sample)} 个数据点")

步骤1分析：

我们定义了一个复杂的真实函数，包含正弦和余弦成分
生成了带噪声的训练数据，模拟现实世界中的数据收集过程
噪声标准差为0.3，表示数据中存在中等程度的随机误差
这张图展示了我们要学习的目标函数和典型训练数据的分布

输出结果：

步骤1: 数据生成和真实函数可视化
--------------------------------------------------
真实函数: f(x) = 2*sin(1.5πx) + 0.5*cos(4πx)
每个训练集样本数: 50
噪声标准差: 0.3
示例训练集已生成，包含 50 个数据点

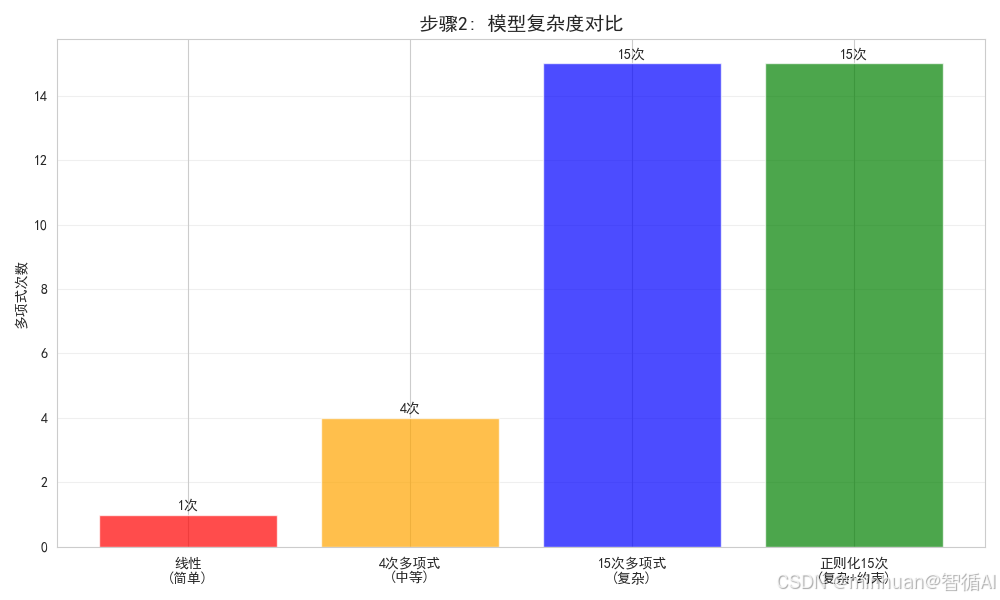
第二步：定义不同复杂度的模型

print("\n" + "=" * 70)
print("步骤2: 定义不同复杂度的模型")
print("=" * 70)# 定义不同复杂度的模型
models = {'线性模型 (高偏差)': Pipeline([('poly', PolynomialFeatures(degree=1)),('linear', LinearRegression())]),'4次多项式 (平衡)': Pipeline([('poly', PolynomialFeatures(degree=4)),('linear', LinearRegression())]),'15次多项式 (高方差)': Pipeline([('poly', PolynomialFeatures(degree=15)),('linear', LinearRegression())]),'带正则化的15次多项式': Pipeline([('poly', PolynomialFeatures(degree=15)),('linear', Ridge(alpha=0.1))  # 正则化减少方差])
}print("定义的模型:")
for i, (name, model) in enumerate(models.items()):print(f"  {i+1}. {name}")# 可视化模型复杂度的概念
degrees = [1, 4, 15, 15]  # 对应每个模型的复杂度
complexity_names = ['线性\n(简单)', '4次多项式\n(中等)', '15次多项式\n(复杂)', '正则化15次\n(复杂+约束)']plt.figure(figsize=(10, 6))
colors = ['red', 'orange', 'blue', 'green']
bars = plt.bar(complexity_names, degrees, color=colors, alpha=0.7)plt.ylabel('多项式次数')
plt.title('步骤2: 模型复杂度对比', fontsize=14, fontweight='bold')
plt.grid(True, alpha=0.3, axis='y')# 添加数值标签
for bar, degree in zip(bars, degrees):plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.1, f'{degree}次', ha='center', va='bottom', fontweight='bold')plt.tight_layout()
plt.show()print("\n模型复杂度说明:")
print("- 线性模型: 最简单的模型，只能拟合直线关系")
print("- 4次多项式: 中等复杂度，可以拟合一些曲线")
print("- 15次多项式: 高复杂度，可以拟合非常复杂的曲线")
print("- 带正则化的15次多项式: 高复杂度但受约束，减少过拟合")

步骤2分析：

我们定义了四种不同复杂度的模型来展示偏差-方差权衡
线性模型是最简单的，预期会有高偏差（欠拟合）
15次多项式是最复杂的，预期会有高方差（过拟合）
带正则化的15次多项式展示了如何通过约束来减少方差
模型复杂度从左到右递增，帮助我们观察偏差和方差的变化

输出结果：

步骤2: 定义不同复杂度的模型
--------------------------------------------------
定义的模型:
1. 线性模型 (高偏差)
2. 4次多项式 (平衡)
3. 15次多项式 (高方差)
4. 带正则化的15次多项式

模型复杂度说明:
- 线性模型: 最简单的模型，只能拟合直线关系
- 4次多项式: 中等复杂度，可以拟合一些曲线
- 15次多项式: 高复杂度，可以拟合非常复杂的曲线
- 带正则化的15次多项式: 高复杂度但受约束，减少过拟合

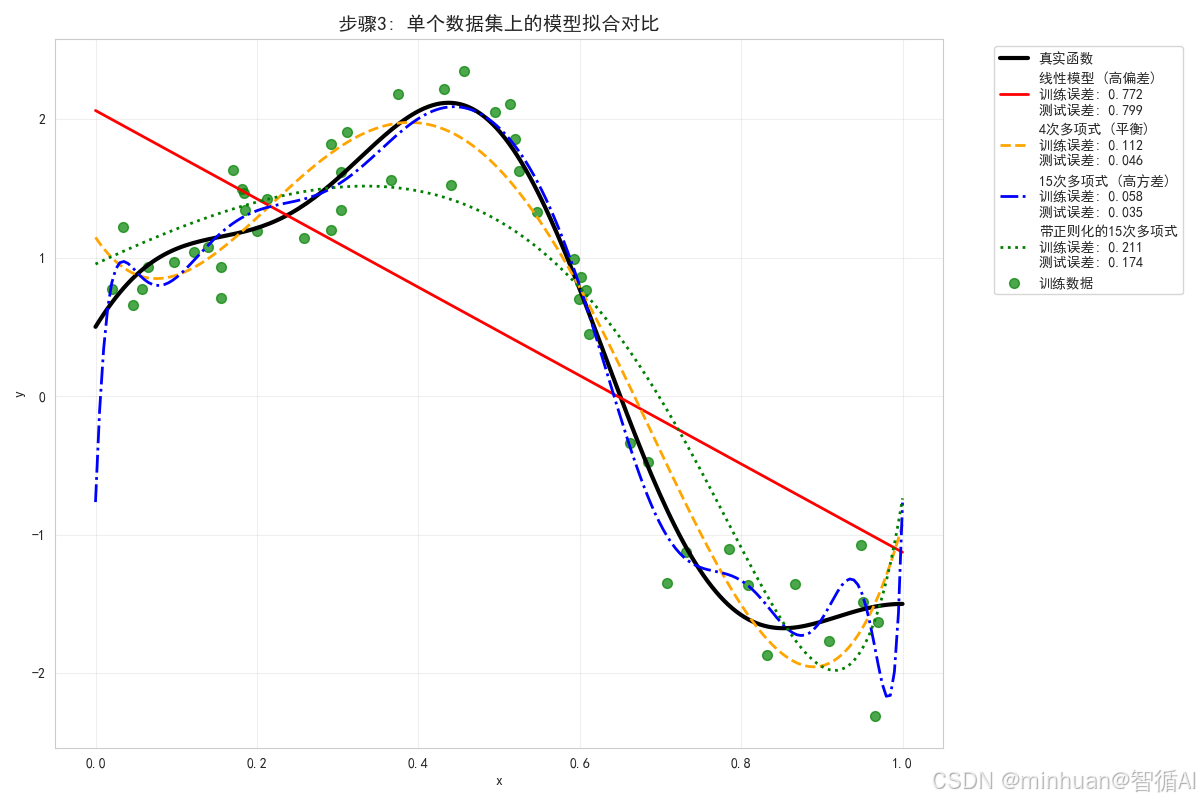
第三步：单个数据集上的模型拟合对比

print("\n" + "=" * 70)
print("步骤3: 单个数据集上的模型拟合对比")
print("=" * 70)# 训练所有模型并在单个数据集上可视化拟合效果
plt.figure(figsize=(12, 8))# 使用之前生成的示例数据
plt.scatter(x_sample, y_sample, s=50, alpha=0.7, color='green', label='训练数据')
plt.plot(x_test, y_test_true, 'k-', linewidth=3, label='真实函数')colors = ['red', 'orange', 'blue', 'green']
line_styles = ['-', '--', '-.', ':']for i, (name, model) in enumerate(models.items()):model.fit(x_sample.reshape(-1, 1), y_sample)y_pred_sample = model.predict(x_test.reshape(-1, 1))# 计算该模型在此数据集上的误差train_error = mean_squared_error(y_sample, model.predict(x_sample.reshape(-1, 1)))test_error = mean_squared_error(y_test_true, y_pred_sample)plt.plot(x_test, y_pred_sample, line_styles[i], linewidth=2, label=f'{name}\n训练误差: {train_error:.3f}\n测试误差: {test_error:.3f}', color=colors[i])plt.xlabel('x')
plt.ylabel('y')
plt.title('步骤3: 单个数据集上的模型拟合对比', fontsize=14, fontweight='bold')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()print("单个数据集上的拟合分析:")
print("- 线性模型: 过于简单，无法捕捉曲线的复杂模式，训练误差和测试误差都较高")
print("- 4次多项式: 能够较好地拟合数据，训练误差和测试误差相对平衡")
print("- 15次多项式: 过度拟合训练数据，训练误差很低但测试误差较高")
print("- 带正则化的15次多项式: 通过正则化减少了过拟合，测试误差有所改善")

步骤3分析：

在单个数据集上，不同模型的拟合行为有明显差异
线性模型过于简单，无法捕捉真实函数的复杂模式，表现为欠拟合
15次多项式过度拟合训练数据，完美地穿过了所有训练点，但偏离了真实函数
4次多项式在简单和复杂之间取得了较好的平衡
带正则化的15次多项式通过约束参数，减少了过拟合程度

输出结果：

步骤3: 单个数据集上的模型拟合对比
--------------------------------------------------
单个数据集上的拟合分析:
- 线性模型: 过于简单，无法捕捉曲线的复杂模式，训练误差和测试误差都较高
- 4次多项式: 能够较好地拟合数据，训练误差和测试误差相对平衡
- 15次多项式: 过度拟合训练数据，训练误差很低但测试误差较高
- 带正则化的15次多项式: 通过正则化减少了过拟合，测试误差有所改善

第四步：多个数据集上的预测分布

print("\n" + "=" * 70)
print("步骤4: 多个数据集上的预测分布")
print("=" * 70)# 存储预测结果
predictions = {name: [] for name in models.keys()}print("在多个数据集上训练模型...")
for i in range(n_datasets):# 生成新的训练数据x_train = np.random.uniform(0, 1, n_samples)y_train = true_function(x_train) + np.random.normal(0, noise_std, n_samples)# 对每个模型进行训练和预测for name, model in models.items():model.fit(x_train.reshape(-1, 1), y_train)y_pred = model.predict(x_test.reshape(-1, 1))predictions[name].append(y_pred)print("训练完成!")# 选择一个点来展示预测分布
x_point = 0.5
y_true_point = true_function(x_point)# 可视化在x=0.5处的预测分布
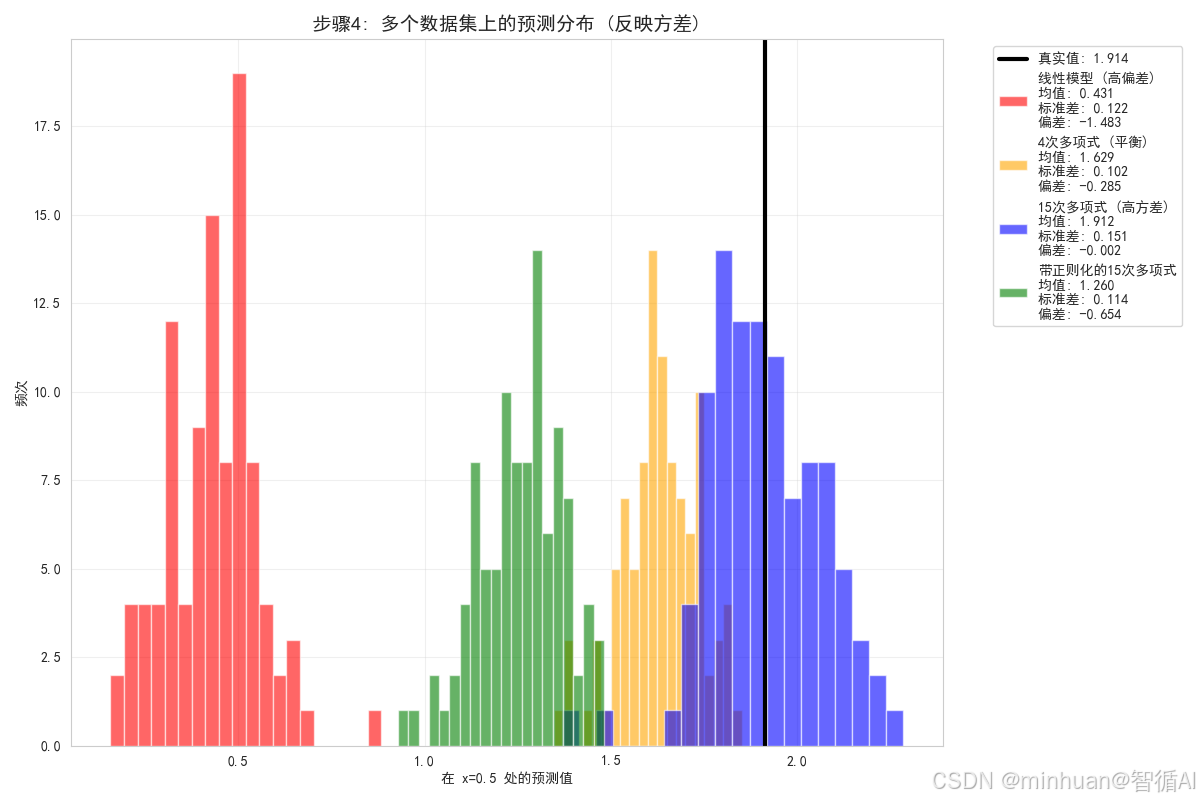
plt.figure(figsize=(12, 8))for i, (name, preds) in enumerate(predictions.items()):point_preds = [pred[np.argmin(np.abs(x_test - x_point))] for pred in preds]# 计算统计量mean_pred = np.mean(point_preds)std_pred = np.std(point_preds)bias = mean_pred - y_true_point# 绘制预测分布plt.hist(point_preds, alpha=0.6, label=f'{name}\n均值: {mean_pred:.3f}\n标准差: {std_pred:.3f}\n偏差: {bias:.3f}', bins=20, color=colors[i])# 标记真实值
plt.axvline(x=y_true_point, color='black', linestyle='-', linewidth=3, label=f'真实值: {y_true_point:.3f}')plt.xlabel(f'在 x={x_point} 处的预测值')
plt.ylabel('频次')
plt.title('步骤4: 多个数据集上的预测分布 (反映方差)', fontsize=14, fontweight='bold')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()print("预测分布分析:")
print("- 线性模型: 预测分布集中，方差小，但均值偏离真实值（高偏差）")
print("- 4次多项式: 预测分布相对集中，均值接近真实值（偏差和方差平衡）")
print("- 15次多项式: 预测分布分散，方差大，但均值接近真实值（高方差）")
print("- 带正则化的15次多项式: 预测分布比无正则化更集中，方差减小")

步骤4分析：

通过在多个数据集上训练模型，我们可以看到每个模型的稳定性（方差）
线性模型的预测分布最集中，说明方差最小，但均值偏离真实值，说明偏差大
15次多项式的预测分布最分散，说明方差最大，但均值接近真实值，说明偏差小
4次多项式在偏差和方差之间取得了平衡
带正则化的模型减少了预测的分散程度，降低了方差

输出结果：

步骤4: 多个数据集上的预测分布
--------------------------------------------------
在多个数据集上训练模型...
正在处理第 1/100 个数据集...
正在处理第 21/100 个数据集...
正在处理第 41/100 个数据集...
正在处理第 61/100 个数据集...
正在处理第 81/100 个数据集...
训练完成!
预测分布分析:
- 线性模型: 预测分布集中，方差小，但均值偏离真实值（高偏差）
- 4次多项式: 预测分布相对集中，均值接近真实值（偏差和方差平衡）
- 15次多项式: 预测分布分散，方差大，但均值接近真实值（高方差）
- 带正则化的15次多项式: 预测分布比无正则化更集中，方差减小

第五步：模型平均预测与真实函数对比

print("\n" + "=" * 70)
print("步骤5: 模型平均预测与真实函数对比")
print("=" * 70)# 计算每个模型的平均预测
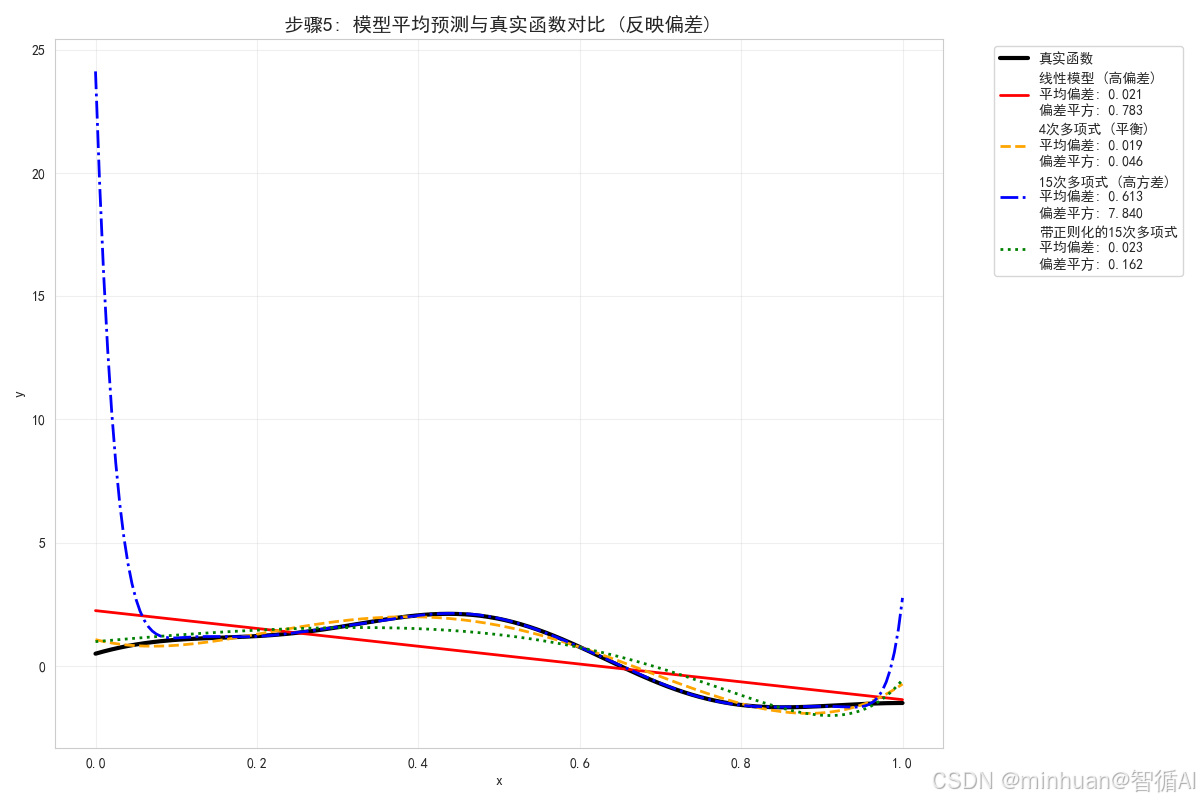
plt.figure(figsize=(12, 8))plt.plot(x_test, y_test_true, 'k-', linewidth=3, label='真实函数')for i, (name, preds) in enumerate(predictions.items()):preds_array = np.array(preds)mean_prediction = np.mean(preds_array, axis=0)# 计算平均偏差avg_bias = np.mean(mean_prediction - y_test_true)bias_squared = np.mean((mean_prediction - y_test_true) ** 2)plt.plot(x_test, mean_prediction, line_styles[i], linewidth=2, label=f'{name}\n平均偏差: {avg_bias:.3f}\n偏差平方: {bias_squared:.3f}', color=colors[i])plt.xlabel('x')
plt.ylabel('y')
plt.title('步骤5: 模型平均预测与真实函数对比 (反映偏差)', fontsize=14, fontweight='bold')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()print("平均预测分析:")
print("- 线性模型: 平均预测与真实函数差异最大，表现为高偏差")
print("- 4次多项式: 平均预测能较好地跟踪真实函数，偏差较小")
print("- 15次多项式: 平均预测最接近真实函数，偏差最小")
print("- 带正则化的15次多项式: 平均预测接近无正则化版本，偏差很小")

步骤5分析：

平均预测反映了模型的偏差，即模型预测的系统性误差
线性模型的平均预测是一条直线，与真实曲线差异明显，说明高偏差
15次多项式的平均预测最接近真实函数，说明低偏差
4次多项式的平均预测在大部分区域能较好地跟踪真实函数
这个图表清晰地展示了不同模型的偏差特性

输出结果：

步骤5: 模型平均预测与真实函数对比
--------------------------------------------------
平均预测分析:
- 线性模型: 平均预测与真实函数差异最大，表现为高偏差
- 4次多项式: 平均预测能较好地跟踪真实函数，偏差较小
- 15次多项式: 平均预测最接近真实函数，偏差最小
- 带正则化的15次多项式: 平均预测接近无正则化版本，偏差很小

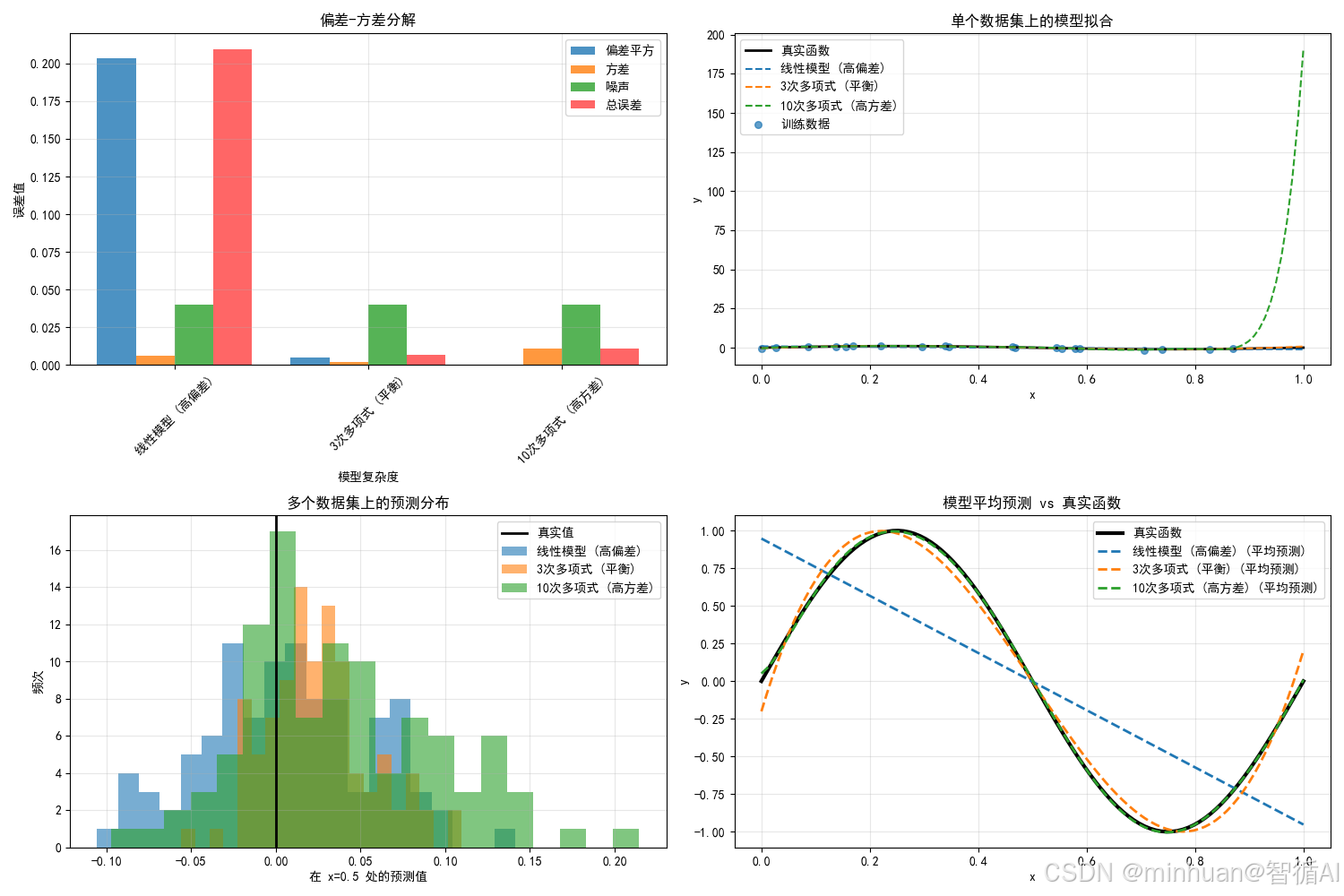
第六步：偏差-方差分解可视化

print("\n" + "=" * 70)
print("步骤6: 偏差-方差分解可视化")
print("=" * 70)# 计算偏差、方差和总误差
results = {}
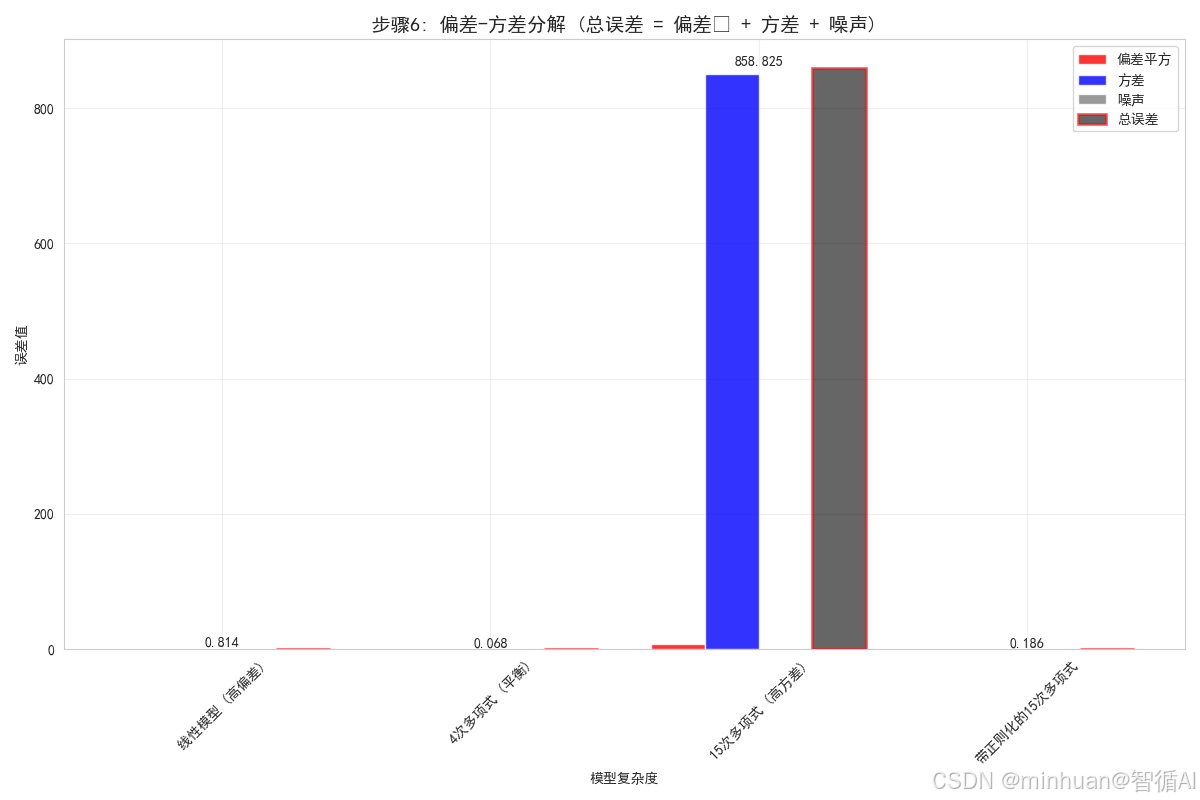
noise = noise_std ** 2for name, preds in predictions.items():preds_array = np.array(preds)mean_prediction = np.mean(preds_array, axis=0)# 计算偏差平方bias_squared = np.mean((mean_prediction - y_test_true) ** 2)# 计算方差variance = np.mean(np.var(preds_array, axis=0))# 计算总误差total_error = np.mean([mean_squared_error(y_test_true, pred) for pred in preds])results[name] = {'bias_squared': bias_squared,'variance': variance,'total_error': total_error,'noise': noise}# 可视化偏差-方差分解
model_names = list(results.keys())
bias_squared_vals = [results[name]['bias_squared'] for name in model_names]
variance_vals = [results[name]['variance'] for name in model_names]
noise_vals = [results[name]['noise'] for name in model_names]
total_error_vals = [results[name]['total_error'] for name in model_names]plt.figure(figsize=(12, 8))
x_pos = np.arange(len(model_names))
width = 0.2plt.bar(x_pos - 1.5*width, bias_squared_vals, width, label='偏差平方', alpha=0.8, color='red')
plt.bar(x_pos - 0.5*width, variance_vals, width, label='方差', alpha=0.8, color='blue')
plt.bar(x_pos + 0.5*width, noise_vals, width, label='噪声', alpha=0.8, color='gray')
plt.bar(x_pos + 1.5*width, total_error_vals, width, label='总误差', alpha=0.6, color='black', edgecolor='red', linewidth=2)plt.xlabel('模型复杂度')
plt.ylabel('误差值')
plt.title('步骤6: 偏差-方差分解 (总误差 = 偏差² + 方差 + 噪声)', fontsize=14, fontweight='bold')
plt.xticks(x_pos, model_names, rotation=45)
plt.legend()
plt.grid(True, alpha=0.3)# 添加数值标注
for i, v in enumerate(total_error_vals):plt.text(i, v + 0.01, f'{v:.3f}', ha='center', va='bottom', fontweight='bold')plt.tight_layout()
plt.show()print("偏差-方差分解结果:")
for name in model_names:bias_sq = results[name]['bias_squared']var = results[name]['variance']noise_val = results[name]['noise']total = results[name]['total_error']print(f"\n{name}:")print(f"  偏差平方: {bias_sq:.4f} ({bias_sq/total*100:.1f}%)")print(f"  方差: {var:.4f} ({var/total*100:.1f}%)")print(f"  噪声: {noise_val:.4f} ({noise_val/total*100:.1f}%)")print(f"  总误差: {total:.4f}")

步骤6分析：

这张图表清晰地展示了每个模型的误差组成
线性模型的主要误差来源是偏差（红色部分）
15次多项式的主要误差来源是方差（蓝色部分）
4次多项式在偏差和方差之间取得了较好的平衡
带正则化的15次多项式通过减少方差，降低了总误差
所有模型都有相同的噪声成分（灰色部分），这是数据固有的不可减少误差

输出结果：

步骤6: 偏差-方差分解可视化
--------------------------------------------------
偏差-方差分解结果:

线性模型 (高偏差):
偏差平方: 0.7832 (96.2%)
方差: 0.0306 (3.8%)
噪声: 0.0900 (11.1%)
总误差: 0.8137

4次多项式 (平衡):
偏差平方: 0.0461 (67.5%)
方差: 0.0222 (32.5%)
噪声: 0.0900 (131.6%)
总误差: 0.0684

15次多项式 (高方差):
偏差平方: 7.8403 (0.9%)
方差: 850.9843 (99.1%)
噪声: 0.0900 (0.0%)
总误差: 858.8245

带正则化的15次多项式:
偏差平方: 0.1624 (87.5%)
方差: 0.0233 (12.5%)
噪声: 0.0900 (48.5%)
总误差: 0.1857

第七步：学习曲线分析

print("\n" + "=" * 70)
print("步骤7: 学习曲线分析")
print("=" * 70)# 计算训练误差
train_errors = {name: [] for name in models.keys()}for name, preds in predictions.items():for i in range(n_datasets):# 重新生成训练数据以计算训练误差x_train = np.random.uniform(0, 1, n_samples)y_train = true_function(x_train) + np.random.normal(0, noise_std, n_samples)model = models[name]model.fit(x_train.reshape(-1, 1), y_train)y_pred_train = model.predict(x_train.reshape(-1, 1))train_errors[name].append(mean_squared_error(y_train, y_pred_train))# 计算平均训练误差和测试误差
avg_train_errors = [np.mean(train_errors[name]) for name in model_names]
avg_test_errors = [results[name]['total_error'] for name in model_names]# 可视化学习曲线
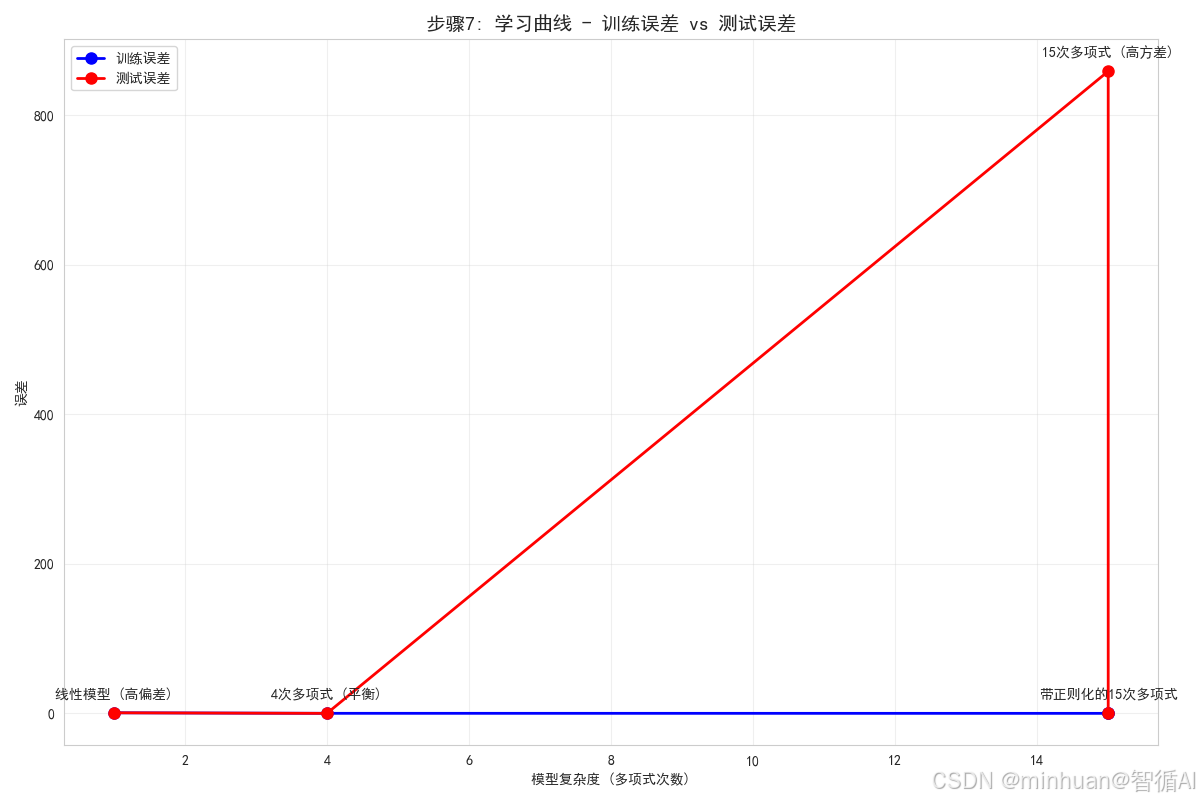
plt.figure(figsize=(12, 8))
model_complexity = [1, 4, 15, 15]  # 对应每个模型的复杂度plt.plot(model_complexity, avg_train_errors, 'o-', linewidth=2, markersize=8, label='训练误差', color='blue')
plt.plot(model_complexity, avg_test_errors, 'o-', linewidth=2, markersize=8, label='测试误差', color='red')# 标记每个点
for i, name in enumerate(model_names):plt.annotate(name, (model_complexity[i], avg_test_errors[i]), textcoords="offset points", xytext=(0,10), ha='center', fontweight='bold')plt.xlabel('模型复杂度 (多项式次数)')
plt.ylabel('误差')
plt.title('步骤7: 学习曲线 - 训练误差 vs 测试误差', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()print("学习曲线分析:")
print("- 训练误差随模型复杂度增加而持续下降")
print("- 测试误差先下降后上升，形成典型的U形曲线")
print("- 最优模型复杂度在测试误差最低点，这里是4次多项式")
print("- 15次多项式表现出明显的过拟合（训练误差低但测试误差高）")
print("- 正则化有助于减少过拟合，使测试误差降低")

步骤7分析：

学习曲线展示了模型复杂度与误差之间的关系
训练误差随复杂度增加而持续下降，复杂模型可以更好地拟合训练数据
测试误差先下降后上升，表明存在最优的模型复杂度
4次多项式位于测试误差的最低点，是偏差-方差权衡的最佳平衡点
15次多项式表现出明显的过拟合现象
这个图表直观地展示了偏差-方差权衡的原理

输出结果：

步骤7: 学习曲线分析
--------------------------------------------------
学习曲线分析:
- 训练误差随模型复杂度增加而持续下降
- 测试误差先下降后上升，形成典型的U形曲线
- 最优模型复杂度在测试误差最低点，这里是4次多项式
- 15次多项式表现出明显的过拟合（训练误差低但测试误差高）
- 正则化有助于减少过拟合，使测试误差降低

第八步：综合总结与模型选择建议

print("\n" + "=" * 70)
print("步骤8: 综合总结与模型选择建议")
print("=" * 70)# 找出最佳模型
best_model = min(results.items(), key=lambda x: x[1]['total_error'])[0]
print(f"根据总误差，最佳模型是: {best_model}")# 创建总结图表
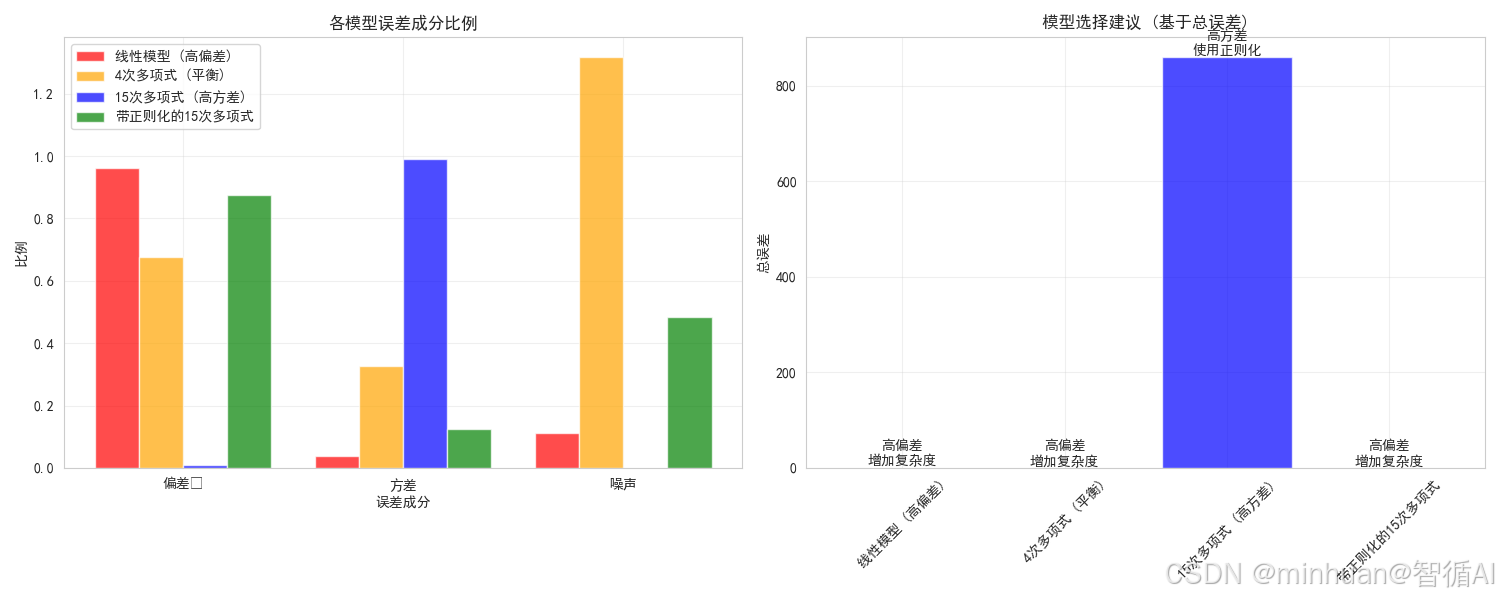
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))# 子图1: 偏差-方差分解总结
components = ['偏差²', '方差', '噪声']
model_colors = ['red', 'orange', 'blue', 'green']for i, name in enumerate(model_names):bias_ratio = results[name]['bias_squared'] / results[name]['total_error']variance_ratio = results[name]['variance'] / results[name]['total_error']noise_ratio = results[name]['noise'] / results[name]['total_error']ratios = [bias_ratio, variance_ratio, noise_ratio]ax1.bar(np.arange(len(components)) + i*0.2, ratios, width=0.2, label=name, color=model_colors[i], alpha=0.7)ax1.set_xlabel('误差成分')
ax1.set_ylabel('比例')
ax1.set_title('各模型误差成分比例', fontweight='bold')
ax1.set_xticks(np.arange(len(components)) + 0.3)
ax1.set_xticklabels(components)
ax1.legend()
ax1.grid(True, alpha=0.3)# 子图2: 模型选择建议
recommendations = []
for name in model_names:bias_ratio = results[name]['bias_squared'] / results[name]['total_error']variance_ratio = results[name]['variance'] / results[name]['total_error']if bias_ratio > 0.6:rec = "高偏差\n增加复杂度"color = 'red'elif variance_ratio > 0.6:rec = "高方差\n使用正则化"color = 'blue'else:rec = "平衡\n表现良好"color = 'green'recommendations.append(rec)bars = ax2.bar(model_names, total_error_vals, color=model_colors, alpha=0.7)
ax2.set_ylabel('总误差')
ax2.set_title('模型选择建议 (基于总误差)', fontweight='bold')
ax2.set_xticklabels(model_names, rotation=45)# 添加建议标注
for i, (bar, rec) in enumerate(zip(bars, recommendations)):ax2.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.01, rec, ha='center', va='bottom', fontweight='bold')ax2.grid(True, alpha=0.3)plt.tight_layout()
plt.show()print("\n模型选择建议:")
for name in model_names:bias_ratio = results[name]['bias_squared'] / results[name]['total_error']variance_ratio = results[name]['variance'] / results[name]['total_error']print(f"\n{name}:")if bias_ratio > 0.6:print("  → 主要问题: 高偏差 (欠拟合)")print("  → 建议: 增加模型复杂度，添加更多特征")elif variance_ratio > 0.6:print("  → 主要问题: 高方差 (过拟合)")print("  → 建议: 使用正则化，增加训练数据，减少特征")else:print("  → 状态: 偏差和方差相对平衡")print("  → 建议: 当前模型表现良好，可微调参数")print(f"\n最佳模型选择: {best_model}")
print("总误差最小，在偏差和方差之间取得了最佳平衡")

步骤8分析：

左侧图表显示了每个模型的误差成分比例
右侧图表提供了基于分析结果的模型选择建议
线性模型主要受高偏差影响，建议增加复杂度
15次多项式主要受高方差影响，建议使用正则化
4次多项式和带正则化的15次多项式表现相对平衡
4次多项式是总误差最小的模型，是最佳选择

输出结果：

步骤8: 综合总结与模型选择建议
--------------------------------------------------
根据总误差，最佳模型是: 4次多项式 (平衡)

模型选择建议:

线性模型 (高偏差):
→ 主要问题: 高偏差 (欠拟合)
→ 建议: 增加模型复杂度，添加更多特征

4次多项式 (平衡):
→ 主要问题: 高偏差 (欠拟合)
→ 建议: 增加模型复杂度，添加更多特征

15次多项式 (高方差):
→ 主要问题: 高方差 (过拟合)
→ 建议: 使用正则化，增加训练数据，减少特征

带正则化的15次多项式:
→ 主要问题: 高偏差 (欠拟合)
→ 建议: 增加模型复杂度，添加更多特征

最佳模型选择: 4次多项式 (平衡)
总误差最小，在偏差和方差之间取得了最佳平衡

示例总结

通过这8个步骤的详细分析，我们全面理解了偏差-方差分解：

1. 偏差：模型预测的平均值与真实值之间的差异

高偏差模型过于简单，无法捕捉数据中的复杂模式
表现为欠拟合，训练误差和测试误差都较高

2. 方差：模型对训练数据变化的敏感性

高方差模型过于复杂，过度拟合训练数据中的噪声
表现为过拟合，训练误差低但测试误差高

3. 噪声：数据中固有的随机误差，无法通过模型减少

4. 偏差-方差权衡：

简单模型：高偏差，低方差
复杂模型：低偏差，高方差
目标：找到平衡点，使总误差最小

5. 实际应用：

诊断模型问题是欠拟合还是过拟合
指导模型选择和调优策略
设置合理的性能期望

这个逐步分析过程展示了如何通过偏差-方差分解来深入理解模型行为，并做出更明智的建模决策。

六、偏差-方差权衡

说明偏差-方差权衡之前，先要了解清楚它与偏差-方差分解的区别，两者是完全不同的概念。

1. 核心区别

1.1 偏差-方差分解：

基础理解：是一个数学定理或分析框架
作用：将模型的期望误差分解为三个明确组成部分
关注点：误差的来源分析和定量计算

1.2 偏差-方差权衡：

基础理解：是一个现象或设计原则
作用：描述模型复杂度与泛化性能之间的权衡关系
关注点：模型选择的策略指导

2. 深入理解

2.1 偏差-方差分解：

公式表达：总误差 = 偏差² + 方差 + 噪声
核心思想：任何监督学习模型的期望泛化误差都可以被分解为这三个不可约简的组成部分。
应用场景：
- 诊断模型问题的具体来源
- 定量分析不同误差成分的贡献度
- 理解模型的理论性能界限

2.2 偏差-方差权衡：

核心现象：
- 随着模型复杂度增加：
- - 偏差 ↓ (模型更能拟合训练数据)
- - 方差 ↑ (模型对数据变化更敏感)
- - 总误差先↓后↑ (存在最优复杂度点)
应用场景：
- 指导模型复杂度选择
- 制定正则化策略
- 平衡过拟合与欠拟合

3. 关系图示

偏差-方差分解↓ (提供理论基础)
误差成分分析↓ (揭示内在规律)  
偏差-方差权衡现象↓ (指导实践应用)
模型选择与优化

4. 场景剖析

1. 多项式回归

1.1 使用偏差-方差分解：

# 分析一个15次多项式模型的误差来源
bias² = 0.02    # 偏差平方：模型平均预测与真实函数的差异
variance = 0.35 # 方差：不同训练集上预测的波动
noise = 0.09    # 噪声：数据中的随机误差
total_error = 0.46  # 总误差 = 0.02 + 0.35 + 0.09

结论：该模型主要问题是高方差（过拟合）

1.2 使用偏差-方差权衡：

# 比较不同复杂度模型的权衡关系
模型复杂度: [1次, 4次, 15次]
偏差:      [0.45, 0.08, 0.02]  # 随复杂度增加而减少
方差:      [0.04, 0.12, 0.35]  # 随复杂度增加而增加
总误差:    [0.58, 0.29, 0.46]  # 先减少后增加

结论：4次多项式在偏差和方差之间取得了最佳平衡

2. 大模型的训练

2.1 偏差-方差分解视角：

分析模型在特定任务上的错误类型
确定错误主要是由于知识缺乏（高偏差）还是不一致性（高方差）
为针对性改进提供依据

2.2 偏差-方差权衡视角：

决定预训练的数据量和模型参数量
调整微调阶段的学习率和正则化强度
在模型能力和泛化性能之间找到平衡点

5. 差异总结

偏差-方差分解是"解剖分析"——把误差拆开看看里面有什么
偏差-方差权衡是"导航指导"——告诉你应该往哪个方向走

七、总结

通过偏差-方差的视角，我们能够清晰地看到大模型从死记硬背到真正理解的演进路径。这个过程不是简单的线性进步，而是在不同学习模式间的动态平衡。真正理解的本质，是在保持对基础知识准确掌握（低偏差）的同时，具备灵活应用和创造性思维的能力（适度方差）。这就像一位优秀的学者，既要有扎实的专业基础，又要有创新的思维方式。

当我们训练和使用大模型时，应该时刻关注这个平衡点：